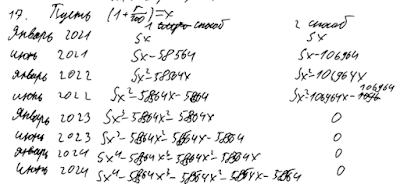15 января был выдан полугодовой кредит на развитие бизнеса в таблице 5 процентов - Контакты компаний и предприятий на Atlaso.ru

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Сайты, меню, вход, новости

Задания

Версия для печати и копирования в MS Word

15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в процентах от кредита)	100%	90%	80%	70%	60%	50%	0%

В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?

Спрятать решение

Решение.

Не снижая общности рассуждений, примем начальную сумму кредита за 100 руб. и будем считать, что выплаты производились 10 числа каждого месяца. Составим таблицу выплат:

Дата	14.02	14.03	14.04	14.05	14.06	14.07
Долг, руб.	105	94,5	84	73,5	63	52,5
Выплата, руб.	15	14,5	14	13,5	13	52,5
Остаток долга на день выплаты, руб.	90	80	70	60	50	0
Остаток долга на день выплаты, %	90%	80%	70%	60%	50%	0%

Тем самым, полная сумма выплат равна 15 + 14,5 +14 +13,5 +13 + 52,5 = 122,5 руб., переплата составила 22,5%.

Ответ: 22,5.

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ	2
Верно построена математическая модель	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	2

Источник: Материалы для экспертов ЕГЭ 2016

Источник

Пусть взяли в кредит a рублей (все суммы в рублях). По условиям задачи заполним в таблице суммы долга на 15-е число каждого месяца (второй столбец таблицы), увеличим на 5 % полученные суммы (третий столбец таблицы). Вычислим платежи каждого месяца, вычитая из числа в
3-м столбце таблицы число во 2-м столбце таблицы строкой ниже.

Месяцев прошло	Долг на 15-е число	Долг в конце месяца	Платёж
0	a	1,05a	0
1	0,9a	0,945a	1,05a – 0,9a = 0,15a
2	0,8a	0,84a	0,945a – 0,8a = 0,145a
3	0,7a	0,735a	0,84a – 0,7a = 0,14a
4	0,6a	0,63a	0,735a – 0,6a = 0,135a
5	0,5a	0,525a	0,63a – 0,5a = 0,13a
6	0	0	0,525a

Сложив все платежи, получим:

0,15a + 0,145a + 0,14a + 0,135a+ 0,13a+ 0,525a = 1,225a.

Общая сумма выплат больше суммы самого кредита на 0,225a, или на 22,5 %.

Ответ. 22,5.

Источник

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

Источник

Задачи ЕГЭ №15 на кредиты обычно относятся к одному из двух характерных типов, которые легко различить между собой.

1 тип. Выплаты кредита производятся равными платежами. Эта схема еще называется «аннуитет»

2 тип. Выплаты кредита подбираются так, что сумма долга уменьшается равномерно. Это так называемая «схема с дифференцированными платежами».

К первому типу относятся также задачи, в которых есть информация о платежах.

Ко второму типу — задачи, в которых есть информация об изменении суммы долга.

В этой статье — решение задач на кредиты второго типа. Схема 2: с дифференцированными платежами. В условии есть информация об изменении суммы долга.

Если в условии задачи сказано, что сумма долга уменьшается равномерно, или что 15-го числа каждого месяца сумма долга на одну и ту же величину меньше суммы долга на 15-е число предыдущего месяца, или есть информация о том, как именно уменьшается сумма долга, — это задача на кредиты второго типа.

1. 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастёт на по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.

Ключевая фраза в условии: «15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца». Другими словами, сумма долга уменьшается равномерно. Что это значит?

Если вначале сумма долга равна S, то через месяц (после начисления процентов и первой выплаты) она уменьшилась до $frac{18}{19}S$ .Еще через месяц будет $frac{17}{19}S$ ,затем $frac{16}{19}S$ — и так до нуля.

Пусть $k=1+frac{r}{100}$

Нарисуем схему погашения кредита.

Первая строка в схеме — сумма долга после очередной выплаты.

Вторая строка — сумма долга после начисления процентов. Стрелками показано, как меняется сумма долга. Число платежных периодов n = 19.

Вот клиент берет в кредит сумму . После начисления процентов сумма долга увеличилась в раз и стала равна . После первой выплаты сумма долга уменьшилась на $frac{1}{19}S$ и стала равной $frac{18}{19}S$ . Банк снова начисляет проценты, и теперь сумма долга равна $frac{18}{19}kS$ . Таким образом, первая выплата

$Z{}_{1}=Scdot k-frac{18}{19}S$

Вторая выплата: $Z_2=frac{18}{19}kS-frac{17}{19}S$

vdots

19-я выплата: $Z_{19}=frac{1}{19}kS$

Сумма всех выплат:

$Z=Z_1+Z_2+cdots +Z_{19}=cdots =$

$=left(kS-frac{18}{19}Sright)+left(frac{18}{19}kS-frac{17}{19}Sright)+cdots +frac{1}{19}kS=$

$=kSleft(1+frac{18}{19}+frac{17}{19}+cdots +frac{1}{19}right)-Sleft(frac{18}{19}+frac{17}{19}+cdots +frac{1}{19}right).$

Мы сгруппировали слагаемые и вынесли общие множители за скобку. Видим, что и в первой, и во второй скобке — суммы арифметической прогрессии, у которой $a_1=frac{1}{19}$ и $d=frac{1}{19}.$

В первой скобке — сумма 19 слагаемых, во второй сумма 18 слагаемых.

По формуле сумма арифметической прогрессии, $S_n=frac{a_1+a_n}{2}cdot n.$

$frac{1}{19}+frac{2}{19}+cdots +1=frac{1}{2}left(frac{1}{19}+frac{19}{19}right)cdot 19=10;$

$frac{1}{19}+frac{2}{19}+cdots +frac{18}{19}=frac{1}{2}left(frac{1}{19}+frac{18}{19}right)cdot 18=9;$

Получим, что общая сумма выплат $Z=10kS-9S=10left(1+frac{p}{100}right)S-9S=S+frac{10p}{100}cdot S=S+Pi$ , где — величина переплаты. Эта величина показывает, на сколько общая сумма выплат больше суммы, взятой в кредит.

В нашей задаче

$Pi =frac{10p}{100}cdot S=frac{n+1}{2}cdot frac{p}{100}cdot S.$

Здесь n=19 — количество платежных периодов.

Получим:

$frac{10p}{100}cdot S=frac{30}{100}S;$

p=3.

Обратите внимание. Общая сумма выплат:

, где — величина переплаты, $Pi=Scdot frac{n+1}{2}cdot frac{p}{100}.$

В следующих задачах мы будем (если это возможно) применять удобную формулу для переплаты без вывода. Однако на экзамене вам надо будет ее вывести. Иначе решение могут не засчитать.

2. 15-го января планируется взять кредит в банке на некоторое количество месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

На сколько месяцев можно взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит.

Пусть $k=1+frac{r}{100}.$

По формуле для переплаты при выплате суммы кредита дифференцированными платежами имеем:

$Pi=frac{n+1}{200}rS$

где — искомое число месяцев, а r = 3 — величина платежной ставки в процентах. По условию, переплата равна 0,3S , тогда:

$0,3S=frac{n+1}{2}cdot 0,03S$

откуда n=19.

3. 15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата	15,01	15,02	15,03	15,04	15,05	15,06	15,07
Долг (в процентах от кредита)	100%	90%	80%	70%	60%	50%	0%

В конце каждого месяца, начиная с января, текущий долг увеличивался на , а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?

В этой задаче (как и в большинстве задач ЕГЭ) мы не сможем применить формулу для величины переплаты. Ведь погашение кредита происходит неравномерно. Первые 5 месяцев долг ежемесячно уменьшается на $frac{1}{10}$ своей величины, а в последний месяц сразу до нуля.

Запишем, чему равна каждая выплата, и найдем сумму всех выплат.

Первая выплата:

Вторая:

Следующие:

Общая сумма выплат

$Z-S=S+4,5cdot 0,05cdot S-S=4,5cdot 0,05S=45cdot frac{5}{1000}S=45cdot frac{5}{10}cdot frac{1}{100}S=22,5cdot frac{1}{100}S=22,5%S$

Pi=Z-S

— переплаты, — общая сумма выплат, — сумма кредита.

Ответ: 22,5%

4. В июле 2016 года планируется взять кредит в размере 6,6 млн. руб. Условия возврата таковы:

— каждый январь долг возрастает на по сравнению с концом предыдущего года.

— с февраля по июнь необходимо выплатить часть долга.

— в июле 2017, 2018 и 2019 годов долг остается равным 6,6 млн. руб.

— суммы выплат 2020 и 2021 годов равны.

Найдите r, если в 2021 году долг будет выплачен полностью и общие выплаты составят 12,6 млн. рублей.

S=6,6 млн.руб

Z=12,6 млн. руб

$k=1+frac{r}{100}$

— ежегодные выплаты 2020 и 2021 годов.

$X=frac{k^2S}{k+1}$

$12,6=3cdot 6,6left(k-1right)+frac{2cdot k^2cdot 6,6}{k+1}$

$126=3cdot 66left(k-1right)+frac{2cdot k^2cdot 66}{k+1}$

$42=66left(k-1right)+frac{44k^2}{k+1}$

$D={21}^2-4cdot 55cdot left(-54right)=12321={111}^2 , Longrightarrow k=frac{132}{110}=frac{12}{10}=frac{120}{100}Longrightarrow r=20%$

Ответ: 20%

В 2018 году появились, пожалуй, самая сложная задачи ЕГЭ такого типа. Вот большая статья о том, что же все-таки было на ЕГЭ-2018:

Разбор задачи №17 («Банковская», или «Экономическая») на ЕГЭ по математике 2018 года.

Подведем итоги. Соберем всё, что узнали о решении задач на кредиты по второй схеме (с дифференцированными платежами) в небольшую таблицу:

Равномерное уменьшение суммы долга (схема с дифференцированными платежами). Применяется также, когда известно, как уменьшается сумма долга.
Пусть – сумма кредита, – количество платежных периодов, – процент по кредиту, начисляемый банком. Коэффициент $k = 1+frac{p}{100}$ показывает, во сколько раз увеличивается сумма долга после начисления процентов.
Схема погашения кредита для платежных периодов. – число платежных периодов. 1 выплата: $Z_1=Scdot k-Scdot frac{n-1}{n}$ 2 выплата: $Z_2= S cdot frac{n-1}{n}cdot k-Scdot frac{n-2}{n}$ n-ная выплата: $Z_n=Scdot frac{1}{n}cdot k$ Сумма всех выплат: $=Scdot kleft (1+frac{n-1}{n}+frac{n-2}{n}+...+frac{1}{n}right )-Sleft ( frac{n-1}{n}+frac{n-2}{n}+...+frac{1}{n} right ).$ Применяем формулу суммы арифметической прогрессии. Общая сумма выплат: $Z= Scdot kcdotfrac{n+1}{2}-Scdotfrac{n-1}{2}=S+Scdotfrac{n+1}{2}cdot frac{p}{100}= S + Pi,$ , где – величина переплаты, $Pi=Scdot frac{n+1}{2}cdot frac{p}{100}.$

Равномерное уменьшение суммы долга (схема с дифференцированными платежами). Применяется также, когда известно, как уменьшается сумма долга.

Пусть

– сумма кредита,

– количество платежных периодов,

– процент по кредиту, начисляемый банком. Коэффициент $k = 1+frac{p}{100}$

показывает, во сколько раз увеличивается сумма долга после начисления процентов.

Схема погашения кредита для

платежных периодов.

– число платежных периодов.

1 выплата: $Z_1=Scdot k-Scdot frac{n-1}{n}$

2 выплата: $Z_2= S cdot frac{n-1}{n}cdot k-Scdot frac{n-2}{n}$

n-ная выплата: $Z_n=Scdot frac{1}{n}cdot k$

Сумма всех выплат:

$=Scdot kleft (1+frac{n-1}{n}+frac{n-2}{n}+...+frac{1}{n}right )-Sleft ( frac{n-1}{n}+frac{n-2}{n}+...+frac{1}{n} right ).$

Применяем формулу суммы арифметической прогрессии. Общая сумма выплат:

$Z= Scdot kcdotfrac{n+1}{2}-Scdotfrac{n-1}{2}=S+Scdotfrac{n+1}{2}cdot frac{p}{100}= S + Pi,$ , где

– величина переплаты,

$Pi=Scdot frac{n+1}{2}cdot frac{p}{100}.$

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Профильный ЕГЭ по математике. Задание № 15. Кредиты. Схема 2: известна информация об изменении суммы долга.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Михаил планирует 15-го декабря взять в банке кредит на 3 года в размере 364 000 рублей. Сотрудник банка предложил Михаилу два различных плана погашения кредита, описание которых приведено в таблице.

План 1

— каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

— кредит должен быть полностью погашен за три года тремя равными платежами.

План 2

— 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг с 1-го по 36-й долг должен быть меньше долга на 15-е число

предыдущего месяца на одну и ту же сумму;

— к 15-му числу 36-го месяца кредит должен быть полностью погашен.

На сколько рублей меньше окажется общая сумма выплат Михаила банку по более выгодному плану погашения кредита?

Пусть X рублей — ежегодный платёж Андрея по плану 1. Тогда

Значит, по плану 1 Андрей заплатит банку всего рублей.

Платежи Андрея по плану 2 составят:

Тогда всего Андрей заплатит банку по плану 2:

рублей.

Значит, по плану 2 общая сумма выплат Андрея банку меньше на рублей.

Редакция Решу ЕГЭ отредактировала условие задачи. В авторской формулировке было: «15-го числа каждого месяца долг с 1-го по 35-й долг должен быть меньше долга на 15-е число предыдущего месяца на одну и ту же сумму». При таком условии возможны любые варианты равномерно уменьшающих долг сумм в первые 35 месяцев и последняя сумма в 36-й месяц, полностью гасящая задолженность.

Источник

15 января был выдан полугодовой кредит на развитие бизнеса в таблице представлен график погашения

15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в процентах от кредита)	100%	90%	80%	70%	60%	50%	0%

Дата	14.02	14.03	14.04	14.05	14.06	14.07
Долг, руб.	105	94,5	84	73,5	63	52,5
Выплата, руб.	15	14,5	14	13,5	13	52,5
Остаток долга на день выплаты, руб.	90	80	70	60	50	0
Остаток долга на день выплаты, %	90%	80%	70%	60%	50%	0%

Тем самым, полная сумма выплат равна 15 + 14,5 +14 +13,5 +13 + 52,5 = 122,5 руб., переплата составила 22,5%.

Источник

15 января был выдан полугодовой кредит на развитие бизнеса в таблице представлен график погашения

15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в процентах от кредита)	100%	90%	80%	70%	60%	50%	0%

Дата	14.02	14.03	14.04	14.05	14.06	14.07
Долг, руб.	105	94,5	84	73,5	63	52,5
Выплата, руб.	15	14,5	14	13,5	13	52,5
Остаток долга на день выплаты, руб.	90	80	70	60	50	0
Остаток долга на день выплаты, %	90%	80%	70%	60%	50%	0%

Тем самым, полная сумма выплат равна 15 + 14,5 +14 +13,5 +13 + 52,5 = 122,5 руб., переплата составила 22,5%.

Источник

15 января был выдан полугодовой кредит на развитие бизнеса в таблице представлен график погашения

15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в процентах от кредита)	100%	90%	80%	70%	60%	50%	0%

Дата	14.02	14.03	14.04	14.05	14.06	14.07
Долг, руб.	105	94,5	84	73,5	63	52,5
Выплата, руб.	15	14,5	14	13,5	13	52,5
Остаток долга на день выплаты, руб.	90	80	70	60	50	0
Остаток долга на день выплаты, %	90%	80%	70%	60%	50%	0%

Тем самым, полная сумма выплат равна 15 + 14,5 +14 +13,5 +13 + 52,5 = 122,5 руб., переплата составила 22,5%.

Источник

15 января был выдан полугодовой кредит на развитие бизнеса в таблице представлен график погашения

Андрей планирует 15-го декабря взять в банке кредит на 3 года в размере 1 655 000 рублей. Сотрудник банка предложил Андрею два различных плана погашения кредита, описание которых приведено в таблице.

План 1

— каждый январь долг возрастает на 10 % по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

— кредит должен быть полностью погашен за три года тремя равными платежами.

План 2

— 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1-го по 36-й долг должен быть меньше долга на 15-е число

предыдущего месяца на одну и ту же сумму;

— 15-го числа 36-го месяца кредит должен быть полностью погашен.

На сколько рублей меньше окажется общая сумма выплат Андрея банку по более выгодному плану погашения кредита?

Пусть X рублей — ежегодный платёж Андрея по плану 1. Тогда

Значит, по плану 1 Андрей заплатит банку всего рублей.

Платежи Андрея по плану 2 составят:

Тогда всего Андрей заплатит банку по плану 2:

рублей.

Значит, по плану 2 общая сумма выплат Андрея банку меньше на рублей.

Источник

4 июня 2021

В закладки

Обсудить

Жалоба

Дифференцированные платежи

Работа с заданием 17.

Задачи: zadachi.pdf
ДЗ: dz.pdf

Первое видео автора по теме

№1.

Даша взяла ипотеку 6 000 000 рублей под 12% годовых на 10 лет. Выплаты подбираются так, чтобы долг уменьшался равномерно.

1) сколько всего денег Даша отдаст банку?
2) На сколько процентов больше Даша отдаст банку по сравнению с суммой, взятой в кредит
3) Сколько процентов составляет сумма выплат по сравнению с суммой, взятой в кредит?
4) Можно ли ответить на вопросы
2) и 3) не зная, сколько денег взяли в кредит?
5) Чему равен 3й платеж?
6) Чему равен наименьший платеж? Наибольший?
7) Сколько выплатит Даша за первые 6 лет?

№2 (ЕГЭ 2016)

Сергей взял в банке кредит 1,2 млн рублей на срок 24 месяца. По договору Сергей должен возвращать в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2%, а затем уменьшается на сумму, уплаченную Сергеем банку в конце месяца. Суммы, выплачиваемые Сергеем, подбираются так, чтобы сумма долга уменьшалась равномерно, т.е. на одну и ту же величину каждый месяц. Какую сумму Сергей вернет банку в течение первого года кредитования?

№3 (ЕГЭ 2016)

Эмиль взял кредит в банке на срок 12 месяцев. По договору Эмиль должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Эмиль погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Эмилем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r.

№4

В июле планируется взять кредит в банке на сумму 18 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы: — каждый январь долг возрастает на 10% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. На сколько лет был взят кредит, если общая сумма выплат после полного погашения кредита составила 27 млн рублей?

№5 (ЕГЭ 2017)

15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения

Источник

15-го
января планируется взять кредит в банке на шесть месяцев в размере
1 млн рублей. Условия его возврата таковы:

— 1-го числа каждого
месяца долг увеличивается на r процентов по
сравнению с концом предыдущего месяца, где r — целое число;

— со 2-го по 14-е число
каждого месяца необходимо выплатить часть долга;

— 15-го
числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.

Дата

15.01

15.02

15.03

15.04

15.05

15.06

15.07

Долг

(в млн рублей)

0,9

0,8

0,7

0,6

0,5

Найдите наименьшее значение r, при котором общая сумма выплат будет больше
1,2 млн рублей.

Ответ: 5.

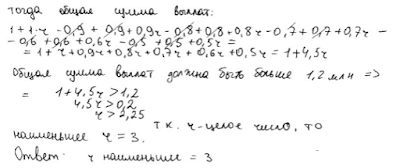
Комментарий.

Модель
построена неверно. Если подставить вместо r число 3 в таблицу, то сумма долга уже на 1 число
второго месяца должна составить 4 млн рублей, кроме того, еще и неравенство
решено неверно.

Оценка эксперта: 0 баллов.

Пример 2.

— со 2-го по 14-е число
каждого месяца необходимо выплатить часть долга;

— 15-го
числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.

Дата

15.01

15.02

15.03

15.04

15.05

15.06

15.07

Долг

(в млн рублей)

0,9

0,8

0,7

0,6

0,5

Найдите наименьшее значение r, при котором общая сумма выплат будет больше
1,2 млн рублей.

Ответ: 5.

Комментарий.

Модель
построена верно. Усложняет проверку отсутствие вычислений. В таблице все
результаты вычислений по формулам, записанным справа, верные. Логика решения
верна.

Оценка эксперта: 3 балла.

Пример 3.

15-го января был выдан полугодовой кредит на развитие
бизнеса. В таблице 15-го января планируется взять кредит в банке на шесть
месяцев в размере 1 млн рублей. Условия его возврата таковы:

— со 2-го по 14-е число
каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен
составлять некоторую сумму
в соответствии со следующей таблицей.

Дата

15.01

15.02

15.03

15.04

15.05

15.06

15.07

Долг

(в млн рублей)

0,9

0,8

0,7

0,6

0,5

Найдите
наименьшее значение r, при котором общая сумма выплат будет больше
1,2 млн рублей.

Ответ: 5.

Пример 4.

В
июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его
возврата таковы:

—
каждый январь долг увеличивается на % по сравнению с концом предыдущего года;

—
с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.

Если
ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за
4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет
полностью погашен за 2 года. Найдите .

Ответ: 10.

Комментарий.

Обоснованно
получен верный ответ.

Оценка эксперта: 3 балла.

Пример 5.

В июле 2020 года планируется взять кредит в банке на некоторую
сумму. Условия его возврата таковы:

—
каждый январь долг увеличивается на % по сравнению с концом предыдущего года;

—
с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.

Ответ: 10.

Комментарий.

В
решении без объяснений записаны уравнения. Переход от системы к уравнению
относительно k не объяснен. Числовой ответ явно не получен: не извлечен
корень из числа 14641. Таким образом, решение недостаточно обоснованное.

Оценка эксперта: 2 балла.

Пример 6.

— 1-го числа каждого
месяца долг увеличивается на процентов по
сравнению с концом предыдущего месяца, где — целое число;

— со 2-го по 14-е число
каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен
составлять некоторую сумму
в соответствии со следующей таблицей.

Дата

15.01

15.02

15.03

15.04

15.05

15.06

15.07

Долг

(в млн рублей)

1

0,9

0,8

0,7

0,6

0,5

0

Найдите
наименьшее значение , при котором общая сумма выплат будет больше
1,2 млн рублей.

Ответ: 5.

Комментарий.

В
решении без объяснений записано неравенство. Неравенство явно не решено. Таким
образом, решение недостаточно обоснованное.

Оценка
эксперта: 2 балла.

Источник

15 января был выдан полугодовой кредит на развитие бизнеса в таблице представлен график погашения

15 января был выдан полугодовой кредит на развитие бизнеса в таблице представлен график погашения

15 января был выдан полугодовой кредит на развитие бизнеса в таблице представлен график погашения

15 января был выдан полугодовой кредит на развитие бизнеса в таблице представлен график погашения

Дифференцированные платежи

Другие крутые статьи на нашем сайте: