632 при совместной работе двух кранов разгрузку баржи закончили за 6 часов

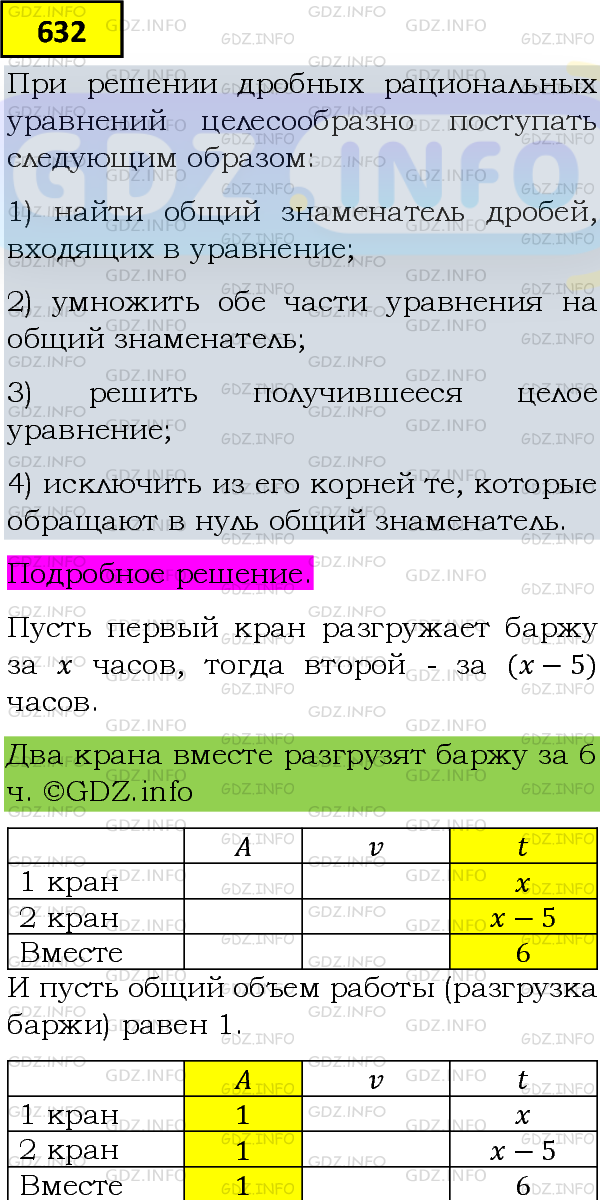
При совместной работе двух кранов разгрузки баржи закончили за 6 ч. Сколько времени потребовалось бы каждому крану отдельно для разгрузки баржи, если известно, что первому крану для этого требуется на 5 ч больше, чем второму?

reshalka.com

ГДЗ учебник по алгебре 8 класс Макарычев. 26. Решение задач с помощью рациональных уравнений. Номер №632

Решение

Пусть x (ч) − время за которое разгружает баржу первый кран, тогда:

x − 5 (ч) − время за которое разгружает баржу второй кран;

1
x

(груза) − разгружает за 1 ч первый кран;

x
−
5

(груза) − разгружает за 1 ч второй кран;

1
6

(груза) − разгружают за 1 оба крана.
Так как,

1
6

груза за 1 ч разгружается двумя кранами, составим уравнение:

1
x

x
−
5

1
6

6
x

+

6

x
−
5

=
1

|x(x − 5)
6(x − 5) + 6x = x(x − 5)

6
x
−
30
+
6
x
=

x
2

−
5
x

x
2

−
17
x
+
30
=
0

D = 289 − 120 = 169

x
=

17
±

169

x
1

17
−
13

4
2

=
2

x
2

17
+
13

30
2

=
15

x ≠ 2, т.к. x − 5 = 2 − 5 = −3 < 0, что невозможно, значит:

x = 15 (ч) − время за которое разгружает баржу первый кран;

x − 5 = 15 − 5 = 10 (ч) − время за которое разгружает баржу второй кран.
Ответ: 15 ч и 10 ч

Источник

Авторы: , Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова.

Издательство:

Просвещение 2015-2022

Тип: Учебник

Подробный решебник (ГДЗ) по Алгебре за 8 (восьмой) класс — готовый ответ номер — 632. Авторы учебника: Макарычев, Миндюк, Нешков, Суворова. Издательство: Просвещение 2015-2022.

Условие /
номер / 632

632. При совместной работе двух кранов разгрузку баржи закончили за 6 ч. Сколько времени потребовалось бы каждому крану отдельно для разгрузки баржи, если известно, что первому крану для этого требуется на 5 ч больше, чем второму?

Решебник к учебнику 2022 / номер / 632

Решебник №1 к учебнику 2015 / номер / 632

Видеорешение / номер / 632

Решебник №2 к учебнику 2015 / номер / 632

Оцените решебник:

4.4/5

5720

Источник

ГДЗ (готовое домашние задание из решебника) на Номер задания №632 по учебнику Алгебра. 8 класс. учебник для общеобразовательных организаций Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова — Просвещение, 2013-2017г.

Условие

При совместной работе двух кранов разгрузку баржи закончили за б ч. Сколько времени потребовалось бы каждому крану отдельно для разгрузки баржи, если известно, что первому крану для этого требуется на 5 ч больше, чем второму?

Решение 1

Подробное решение

Рекомендовано

Белый фонпереписывать в тетрадь

Цветной фонтеория и пояснения

Решение 2

Решение 3

Решение(я) 632 из

26. Решение задач с помощью рациональных уравнений. стр 144-148
,
§9. ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
,
Алгебра. 8 класс. Учебник. Макарычев, Миндюк, Нешков, Суворова

показать содержание

Условие(я):

Условие(я) задания(й):

Нажми по картинке c решением и она увеличится

Ответ(ы):

Оцени решение:

Алгебра. 8 класс. Учебник. Макарычев, Миндюк, Нешков, Суворова

ГДЗ: Правильный(е) ответ(ы) или решения(е) 632
из
26. Решение задач с помощью рациональных уравнений. стр 144-148
, §9. ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ ,
Алгебра. 8 класс. Учебник. Макарычев, Миндюк, Нешков, Суворова

Источник

При совместной работе двух кранов разгрузку баржи закончили за 6 часов.

Сколько времени потребовалось бы каждому крану отдельно для разгрузки баржи, если известно, что первому крану для этого требуется на 5 часов больше чем второму.

Вы открыли страницу вопроса При совместной работе двух кранов разгрузку баржи закончили за 6 часов?. Он относится к категории
Алгебра. Уровень сложности вопроса – для учащихся 5 — 9 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Алгебра,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.

Источник

Решение задач на выполнение работы.

Как правило, учащимся
достаточно сложно дается решение задач на составление уравнений. Это касается и
задач о работе. Но, если еще в среднем звене, дать опыт решения в игровой
форме, то это дает возможность переноса опыта решения игровых задач на решение
любых, практически любой сложности.

Задача №1.

Пусть двое красят
стену. Стена – прямоугольник. Приходит шустрик и красит всю стену за 3
часа. Какую часть стены он покрасит за 1 час? Из начальной школы дети выносят
опыт нахождения части на рисунке, затем при изучении дробей много работают с
моделями, поэтому назвать часть и заштриховать ее на рисунке не составляет
труда.

К такой же стене
приходит мямлик и выполняет всю работу за 5 часов. Какую часть стены он
покрасит за 1 час? Выполняется штриховка.

Показать на рисунке и
ответить на вопрос: какая работа будет выполнена шустриком за 3 часа и мямликом
за 5 часов. Дети убеждаются в том, что вся работа выполнена, а в результате
проделанного с числами действия в ответе получается число 1. Это число
толкуется как полностью покрашенная одна стена. Делается упор на число 1.

К такой же стене
одновременно подходят шустрик и мямлик. Вопрос: — Какую часть стены они
покрасят за час? Эта часть закрашивается на рисунке и записывается как
действие. Обсуждается вопрос о том, что, если данную сумму умножить на время
совместной работы, то в овеете получится 1, что толкуется опять, как полностью
покрашенная одна стена.

Решение дробных
рациональных уравнений в 8 классе

основывается на
данной схеме.

Задача №632.

При совместной работе
двух кранов разгрузку баржи закончили за 6 часов. Сколько времени потребовалось
бы каждому крану отдельно для разгрузки баржи, если известно, что первому крану
для этого требуется на 5 часов больше, чем второму?

Пусть второму крану
для выполнения всей работы требуется х часов, тогда первому крану для
выполнения всей работы необходимо ( х+5) часов. Второй выполняет за час 1/х
часть работы, а первый 1/х+5 часть работы. Вместе за час они выполнят (1/х +
1/х+5 ) часть работы, умножаем на время совместной работы, т. Е. на 6 часов.
Вся работа выполнена, в ответе получаем 1 разгруженную баржу. Все этапы решения
можно комментировать на аналогичных рисунках.

Эта схема работает и
при рассмотрении задачи экзаменационного материала под редакцией С. А.
Шестакова.

Рассмотрим работу №5,
где данная задача приводится, как более сложная.

Карлсон съедает банку
варенья за20 минут, фрекен Бок – за 24 минуты, а Малыш – за 30 минут. За
сколько минут они съедят эту банку варенья втроем.

Если рассмотреть
поедание варенья как совместную работу ложками, то задача сводится к этой же
схеме. И итогом этой совместной работы будет опять число один, трактуемое, как
полностью опустошенная одна банка.

1/20 часть всего
варенья съедается за минуту Карлсоном,

1/24 –фрекен Бок,

1/30 – Малышом.

Объем совместной
работы ,выполненный за 1 минуту, умножается на х минут совместной работы
ложками, получаем итог – одну пустую банку.

При таком
рассмотрении задач учащимся становится понятно, что работа выполнена, когда
вспахано 1 поле, покрашена 1 стена, сделан 1 ящик деталей и т.д., понятие
единицы в правой части равенства делается логичным, осязаемым, а значит, на
базе данных элементарных задач легче строится система рассуждений по более
сложным задачам на выполнение работы.

Источник