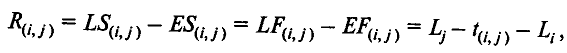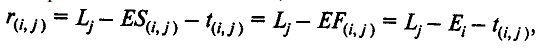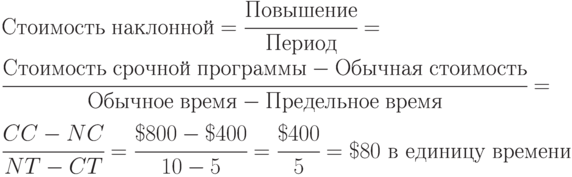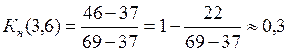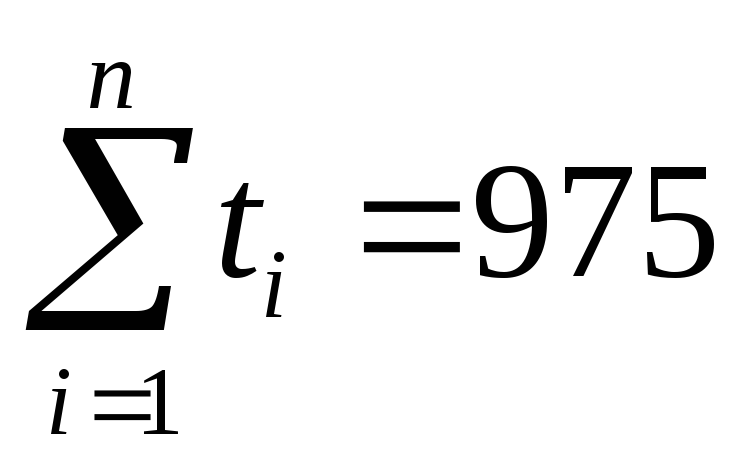Самостоятельно
очертить задачу и определить цель плана.
Построить дерево иерархии, содержащее
не менее трех уровней, от четырех до
семи критериев и не менее трех альтернатив.
Применить к поставленной задаче метод
МАИ для выбора наиболее желательной
альтернативы.
Практика
№4
Сетевой анализ проектов. Метод срм Цели
В
данной главе показаны возможности
использования метода СРМ
(Critical
Path
Method
— метод
критического пути) для контроля сроков
выполнения проекта. Таким проектом
может быть разработка нового продукта
или производственного процесса,
строительство предприятия, здания или
сооружения, ремонт сложного оборудования
и т.д.
При реализации
проекта составляется график выполнения
работ. Для того чтобы проект был завершен
вовремя, необходимо контролировать
сроки выполнения этих работ. Усложняющим
фактором является то, что работы
взаимосвязаны. Одни работы зависят от
выполнения других и не могут начаться,
пока предшествующие работы не будут
завершены.
Важной
предпосылкой применения метода СРМ
является предположение о том, что
время
выполнения
каждой работы точно известно. В
результате использования метода СРМ
удается
получить ответы на следующие вопросы:
-
За какое минимальное
время можно выполнить проект? -
В какое время
должны начаться и закончиться отдельные
работы? -
Какие работы
являются «критическими» и должны быть
выполнены точно в установленное время,
чтобы не был сорван срок выполнения
проекта? -
На
какое время можно отложить срок
выполнения «некритической» работы,
чтобы она не повлияла на срок
выполнения проекта в целом?
После того как вы
выполните задания, предлагаемые в этой
главе, вы будете уметь определять и
использовать для экономического анализа:
-
наиболее раннее
и наиболее позднее время начала работы; -
наиболее раннее
и наиболее позднее время окончания
работы; -
критический путь;
-
длину критического
пути; -
запас времени на
выполнение работы.
Модели
Исходным
шагом для применения метода СРМ
является описание
проекта в виде перечня выполняемых
работ
с указанием их взаимосвязи. Для описания
проекта используются два основных
способа: табличный
и
графический.
Рассмотрим следующую
таблицу, описывающую проект:
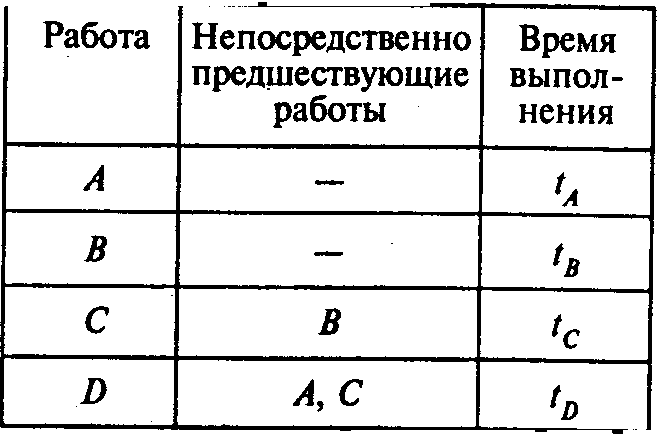
В
первом столбце указаны наименования
всех работ проекта. Их четыре: А,
В, С, D.
Во
втором столбце указаны работы,
непосредственно предшествующие данной.
У работ А
и
В
нет
предшествующих. Работе С
непосредственно
предшествует работа В.
Это
означает, что работа С
может
быть начата только после того, как
завершится работа В.
Работе
D
непосредственно
предшествуют две работы: А
и
С. Это означает, что работа D
может
быть начата только после того, как
завершатся работы А
и
С.
В третьем
столбце таблицы для каждой работы
указано время ее выполнения. На основе
этой таблицы может быть построено
графическое описание проекта (рис. 1).
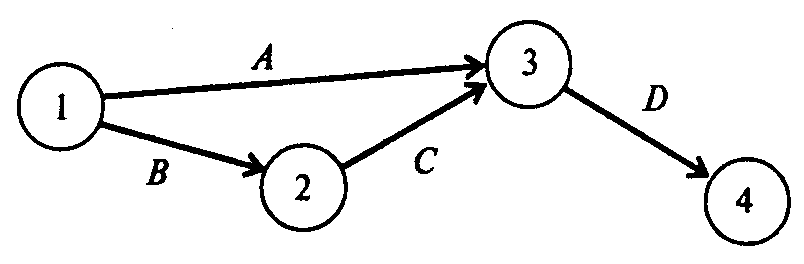
Рис. 1
На
рис. 1 проект представлен в виде графа
с вершинами 1,2, 3, 4 и дугами А,
В, С, D.
Каждая
вершина графа отображает событие.
Событие 1 означает начало выполнения
проекта. Иногда такое событие обозначают
буквой s
(start).
Событие
4 означает завершение проекта. Для
обозначения такого события
иногда используют букву
f(
finish).
Любая
работа проекта — это упорядоченная
пара двух событии.
Например, работа А
есть
упорядоченная пара событий (1, 3)(см. рис.
1). Работа D
— упорядоченная
пара событий (3,4). Событие проекта состоит
в том, что завершены все работы, «входящие»
в соответствующую вершину. Например,
событие 3 состоит в том, что завершены
работы А
и
С.
Рассмотрим другой
проект, представленный следующей
таблицей:
80
|
Работа |
Непосредственно предшествующие работы |
Время выполнения |
|
А |
— |
tA |
|
В |
— |
tB |
|
С |
В |
tC |
|
D |
А, С |
tD |
|
Е |
С |
tE |
|
F |
С |
tF |
|
G |
D,E,F |
TG |
Графическое
описание проекта, построенное по этой
таблице, имеет вид, показанный на рис.
2.
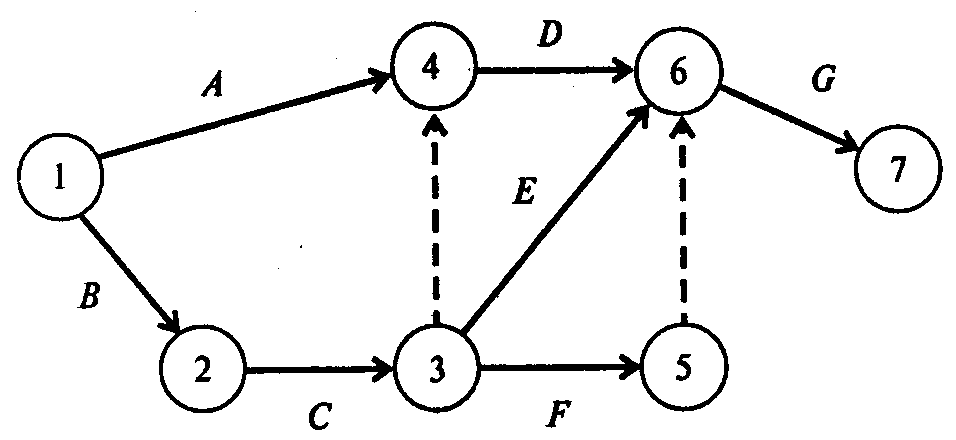
Рис.2
В
этом графическом описании проекта,
кроме тех работ, которые указаны в
таблице, использованы две «фиктивные»
работы (3, 4) и (5, 6). На рисунке они показаны
штриховыми линиями. Эти работы не требуют
времени на их выполнение и используются
в графическом представлении проекта
лишь для того,
чтобы правильно отобразить взаимосвязь
между работами. Получив графическое
представление проекта,
мы обеспечили себе возможность провести
расчеты методом СРМ.
Определения:
Путь
— последовательность
взаимосвязанных работ, ведущая из одной
вершины проекта в другую вершину.
Например, {A,
D,
G}
и {В,
С, Е, С}
—
два
различных пути, ведущие из вершины 1 в
вершину 7 (см. рис. 2).
Длина
пути — суммарная
продолжительность выполнения всех
работ пути.
Критический
путь — путь,
суммарная продолжительность выполнения
всех работ которого является наибольшей.
Ясно,
что минимальное время, необходимое для
выполнения любого проекта, равно длине
критического пути.
Именно на работы, принадлежащие
критическому пути, следует обращать
особое внимание. Если
такая работа будет отложена на некоторое
время, то и срок окончания проекта будет
отложен на то
же время. Если необходимо сократить
время выполнения проекта, то в первую
очередь нужно сократить время выполнения
хотя бы одной работы на критическом
пути.
Для
того чтобы найти критический путь,
достаточно перебрать все пути и выбрать
тот или те из них, что имеют
наибольшую суммарную продолжительность
выполнения работ. Однако для больших
проектов
реализация такого подхода связана с
вычислительными трудностями. Метод СРМ
позволяет
получить
критический путь намного проще.
Пусть
i
и
j
— вершины,
или события, проекта, (i,j)
— работа
проекта, s
— событие
«начало проекта» (start),
f
— событие
«окончание проекта» (finish),
Т — длина
критического пути.
Введем следующие
обозначения:
t(i,j)
—
время выполнения работы (i,
j);
ES(i,j)
—наиболее
раннее время начала работы (i,j);
EF(i,j)
—наиболее раннее время окончания работы
(i,j);
LS(i,j)
—наиболее позднее время начала работы
(i,j),
LF(i,j)
— наиболее позднее время окончания
работы (i,j),
Ei
— наиболее
раннее время наступления события i;
Li
— наиболее
позднее время наступления события i;
R(i,j)
—
полный резерв времени на выполнение
работы (i,j)
(время,
на которое может быть отложена работа
(i,j)
без
увеличения продолжительности выполнения
всего проекта);
r(i,j)
— свободный
резерв времени на выполнение работы
(ij)
(время,
на которое может быть
отложена
работа (i,j)
без
увеличения наиболее раннего времени
Et
наступления
последующего
события/).
Если
(i,j)
— работа
проекта, то имеют место соотношения:
для любого
j
ES(ij)
= Е; для
любого i
LF(i,j)
= Ц. Для
того чтобы использовать метод СРМ
для
нахождения критического пути, необходимо
для каждой
работы
(ij)
определить
наиболее раннее время начала и окончания
работы (ES(ij)
и
EF(ij))
и
н
аиболее
позднее время начала и окончания работы
(LS(ij)
и LF(ij)).
Метод
СРМ
описывается
следующими соотношениями:
(1)
для
любой работы (sj),
выходящей
из стартовой вершины s
проекта;
EF
(I,j)
= ES(i,j)+t(i,j)=Ei+t(i,j)(2)
(3)
т
.е.
наиболее раннее время окончания любой
работы (i,j)
превышает
наиболее раннее время начала этой
работы (время наступления предшествующего
события i)
на время
ее выполнения;
из
значений наиболее раннего, т.е. наиболее
раннее время начала работы (q,
j)
равно
наибольшему времени
окончания непосредственно предшествующих
ей работ;
(4)
т.е. длина
критического пути равна наиболее
раннему времени завершения проекта;
(
5)
т.е. наиболее
позднее время окончания любой работы,
завершающей проект, равно длине
критического пути;
(6)
т.е. наиболее
позднее время начала любой работы
меньше наиболее позднего времени
окончания этой
р
аботы
(времени наступления последующего
события) на время ее выполнения;
(
7)
т.е.
наиболее позднее время окончания работы
(/, q)
равно
наименьшему из значений наиболее
позднего времени
начала непосредственно следующих за
ней работ;
(8)
т
.е.
полный резерв времени на выполнение
любой работы равен разности между
наиболее поздним и наиболее ранним
временем ее начала или разности между
наиболее поздним и наиболее ранним
временем ее окончания;
(9)
(9)
т.е. свободный
резерв времени на выполнение любой
работы равен разности между наиболее
поздним временем наступления последующего
события и наиболее ранним временем
окончания работы.
Из приведенных
выше определений и соотношений
непосредственно вытекают следующие
утверждения:
-
Длина
критического пути равна Т. -
Если
R(i,j)
=
0, то работа (i,j)
лежит
на критическом пути; если R(i,j)
> 0, то работа (i,j)
не
лежит на критическом пути.
-
Если
время начала работы (i,j),
не
лежащей на критическом пути, отложить
на срок меньший, чем r(i,j),
то наиболее раннее время наступления
последующего события не изменится. -
Если
время начала работы (i,j),
не
лежащей на критическом пути, отложить
на срок меньший, чем R(i,j),
то
время, необходимое на выполнение всего
проекта, не увеличится.
Примеры
Пример
1. Реконструкция
торгового центра.
Департамент
Юго-Западного округа Москвы рассматривает
возможность реконструкции торгового
центра у станции метро «Юго-Западная».
После сноса старых палаток проектом
предусматривается
82
строительство
павильонов для сдачи их в аренду торговым
фирмам. Работы, которые необходимо
выполнить при реализации проекта, а
также их взаимосвязь и время выполнения
указаны в следующей таблице:
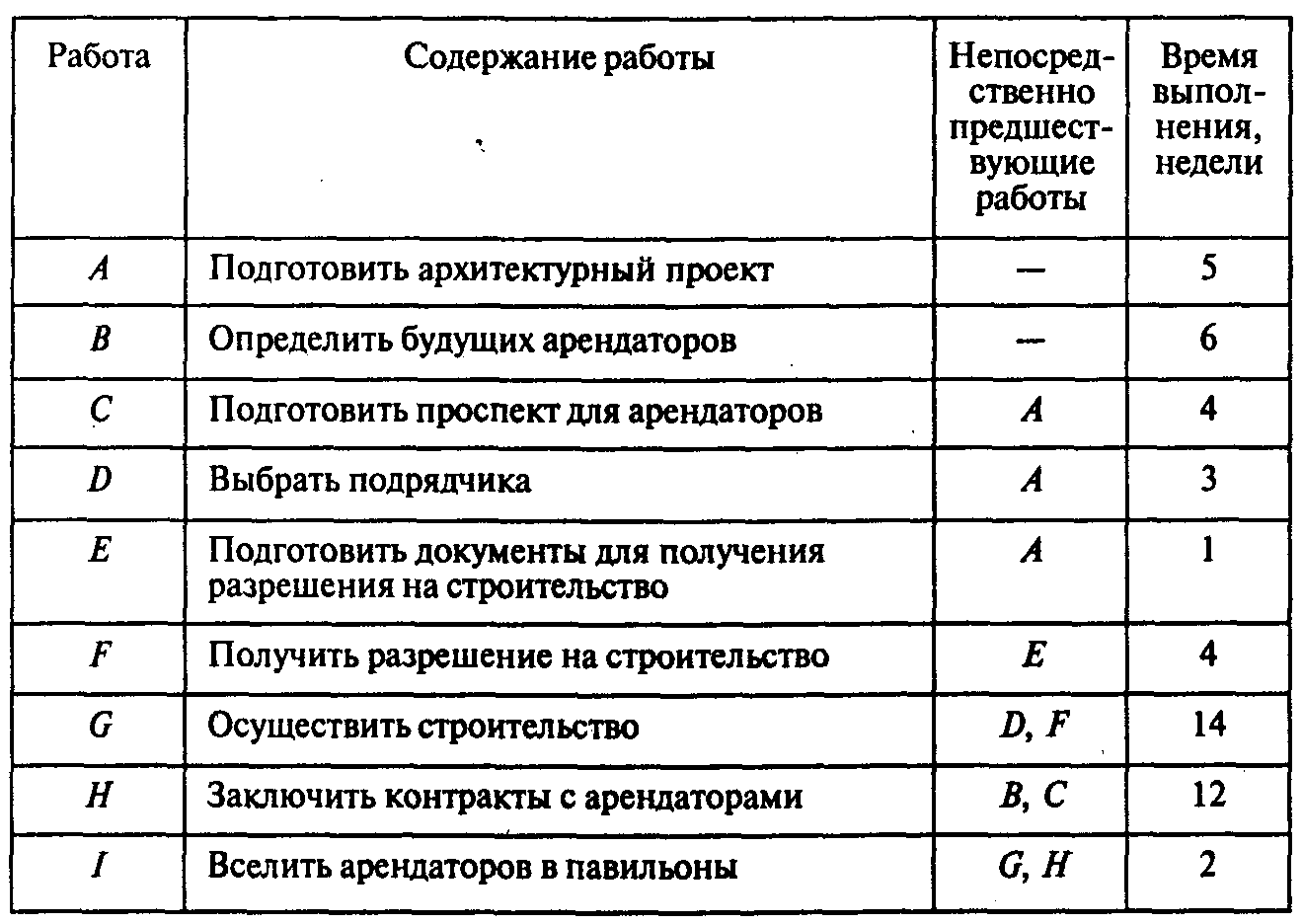
Вопросы:
-
Сколько работ на
критическом пути? -
Какова длина
критического пути? -
На
сколько недель можно отложить начало
выполнения работы Е,
чтобы
это не повлияло на срок выполнения
проекта? -
На
сколько недель можно отложить начало
выполнения работы В,
чтобы
это не повлияло на срок выполнения
проекта (полный резерв времени)? -
На
сколько недель можно отложить начало
выполнения работы С,
чтобы это не изменило наиболее поздний
срок наступления последующего события
(свободный резерв времени)?
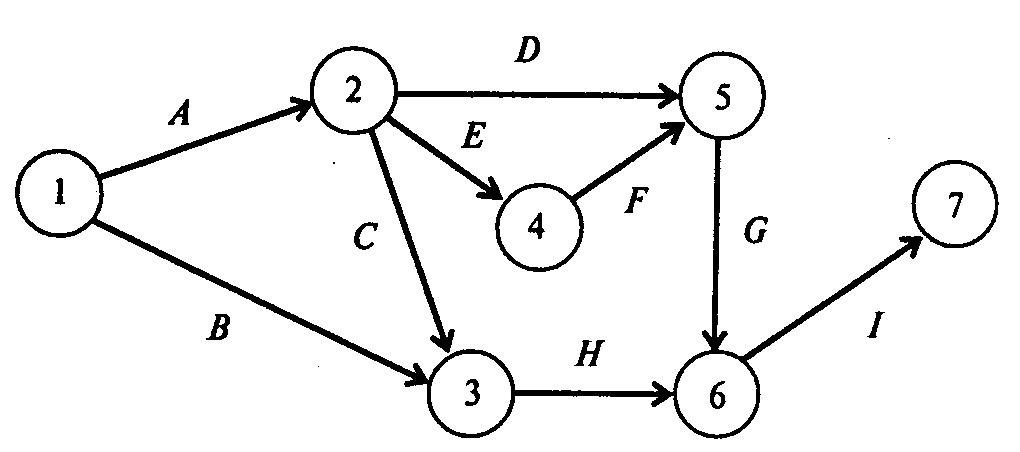
Решение.
Для
того чтобы определить срок выполнения
проекта, достаточно найти длину
критического пути. Для этого построим
графическое представление проекта
(рис. 3).
Рис.3
Критический
путь для этого проекта может быть найден
с помощью прямых расчетов по методу
СРМ,
описанному
в разделе «Модели». Те же результаты
можно получить, воспользовавшись
программой POMWIN.
Для
этого достаточно ввести в программу
исходную информацию, описывающую проект
в виде следующей таблицы:
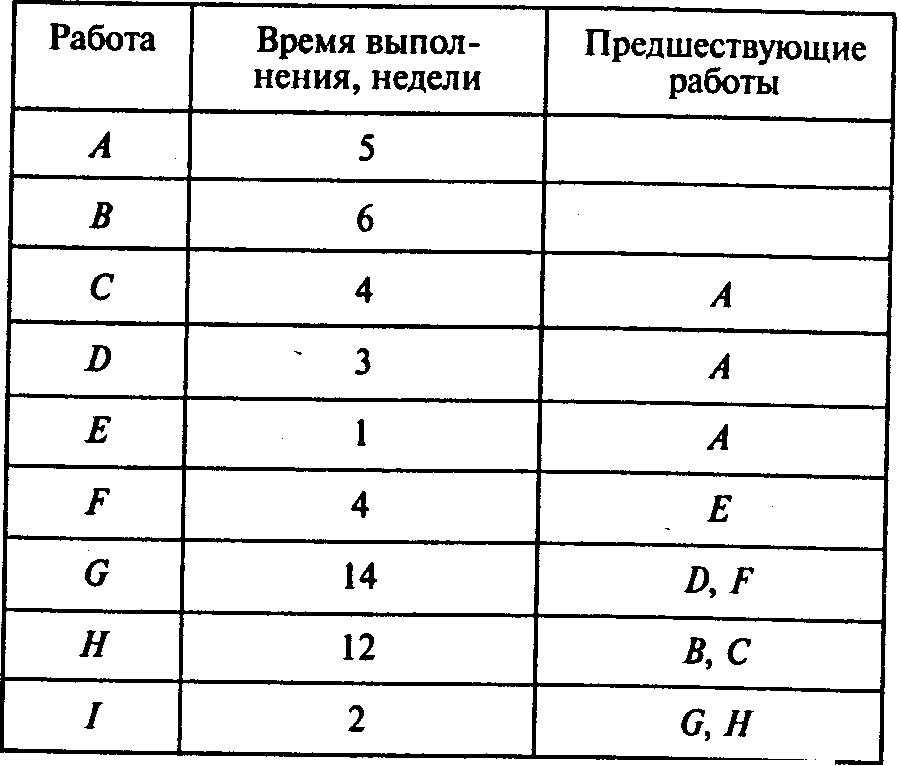
Результаты расчетов будут
представлены в виде следующей таблицы:
|
Project |
26 |
|||||
|
Работа |
Время |
ES |
EF |
LS |
LF |
R |
|
A |
5 |
0 |
5 |
0 |
5 |
0 |
|
В |
6 |
0 |
6 |
6 |
12 |
6 |
|
С |
4 |
5 |
9 |
8 |
12 |
3 |
|
D |
3 |
5 |
8 |
7 |
10 |
2 |
|
Е |
1 |
5 |
6 |
5 |
6 |
0 |
|
F |
4 |
6 |
10 |
6 |
10 |
0 |
|
G |
14 |
10 |
24 |
10 |
24 |
0 |
|
H |
12 |
9 |
21 |
12 |
24 |
3 |
|
I |
2 |
24 |
26 |
24 |
26 |
0 |
Эта
таблица содержит информацию, позволяющую
ответить на все вопросы задачи. Строка
«Project 26» указывает на то, что длина
критического пути равна 26. На критическом
пути лежат все работы, значения
резерва времени которых, указанные в
последнем столбце, равны нулю. Это
работы А,
Е, F,
G,
I.
Таким
образом, если отложить начало работы
Е,
то
срок выполнения проекта увеличится. В
то же время работу
В
можно
начать не в нулевой момент времени, а
в момент 6, т.е. начало выполнения работы
В
можно
отложить на 6 недель. Критический путь
для этого проекта показан на рис. 4
полужирными стрелками.
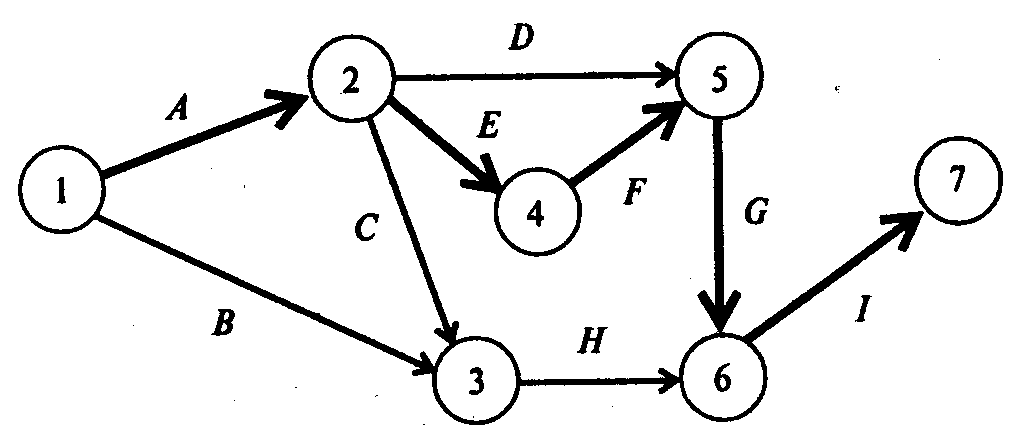
Рис. 4
Возможен
другой способ введения исходной
информации в программу POMWIN.
Этот
способ использует графическое
представление проекта и как следствие
описывает дуги в виде пары вершин.
Соответствующее описание проекта
приведено в следующей таблице:
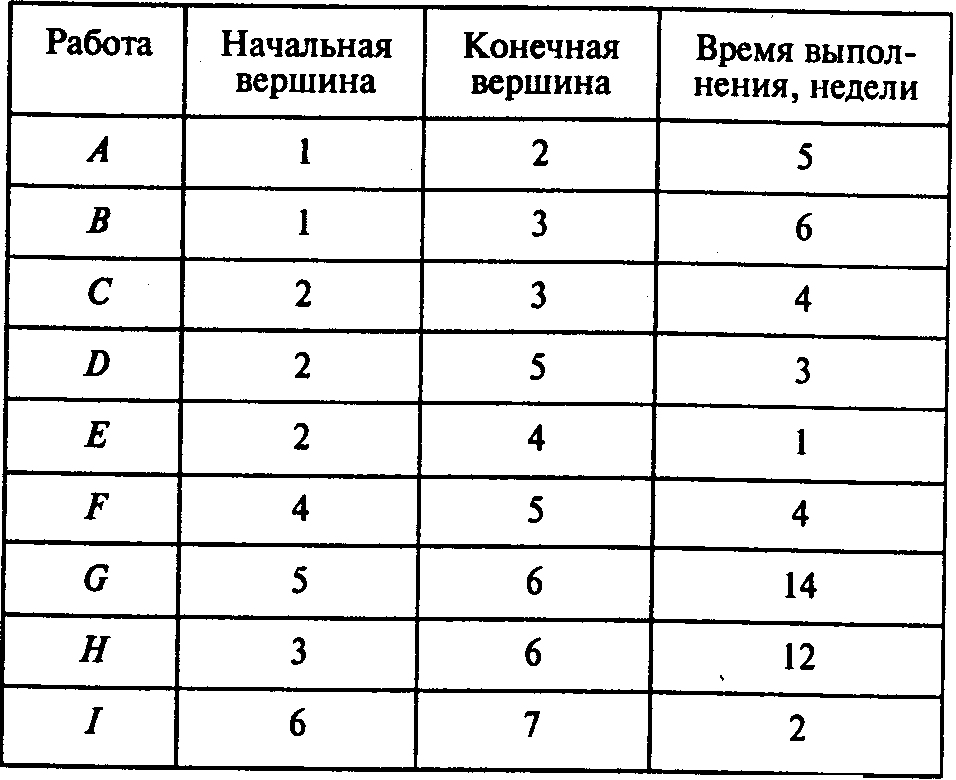
Результаты расчетов
будут представлены в виде следующей
таблицы:
|
Project |
26 |
|||||||
|
Работа |
Начальная |
Конечная |
Время |
£5 |
EF |
15 |
LF |
R |
|
A |
1 |
2 |
5 |
0 |
5 |
0 |
5 |
0 |
|
В |
1 |
3 |
6 |
0 |
6 |
б |
12 |
6 |
|
С |
2 |
3 |
4 |
5 |
9 |
8 |
12 |
3 |
|
D |
2 |
5 |
3 |
5 |
8 |
7 |
10 |
2 |
|
Е |
2 |
4 |
1 |
5 |
6 |
5 |
6 |
0 |
|
F |
4 |
5 |
4 |
6 |
10 |
6 |
10 |
0 |
|
G |
5 |
6 |
14 |
10 |
24 |
10 |
24 |
0 |
|
H |
3 |
6 |
12 |
9 |
21 |
12 |
24 |
3 |
|
I |
6 |
7 |
2 |
24 |
26 |
24 |
26 |
0 |
Ответы:
1. Пять работ. 2. 26 недель. 3. Начало
выполнения работы E
отложить
нельзя. Ответ — 0. 4.
На шесть недель. 5. На три недели.
Вопросы
Вопрос
1. Метод
СРМ
разработан
для:
-
описания проектов
путем указания всех работ, предшествующих
данной работе; -
описания проектов
путем представления каждой работы в
виде пары узлов сети; -
минимизации
издержек на сокращение продолжительности
проекта; -
нахождения
критического пути для проектов с
заданным временем выполнения каждой
работы; -
нахождения
критического пути для проектов с
неопределенным временем выполнения
работ. Вопрос
2. Узел-событие
сетевого графика выражает результат:
-
начаты все работы,
выходящие из узла; -
закончены все
работы, входящие в узел; -
начата хотя бы
одна работа, выходящая из узла; -
закончена хотя
бы одна работа, входящая в узел; -
закончены
все работы, входящие в узел, и начата
хотя бы одна работа, выходящая из узла.
Вопрос
3. Наиболее
раннее время наступления события равно:
-
минимальной длине
пути из данного узла в конечный; -
максимальной
длине пути из данного узла в конечный; -
максимальной
длине пути из начального узла в данный; -
максимальному
времени наиболее раннего окончания
работ, входящих в данный узел; -
минимальному
времени наиболее позднего начала работ,
выходящих из данного узла. Вопрос
4. Наиболее
позднее время наступления события
равно:
-
Минимальной длине
пути из данного узла в конечный; -
максимальной
длине пути из данного узла в конечный;
-
максимальной
длине пути из начального узла в данный; -
максимальному
времени наиболее раннего начала работ,
выходящих из данного узла; -
минимальному
времени наиболее позднего начала работ,
выходящих из данного узла. Вопрос
5. Для
того чтобы сократить время выполнения
проекта, необходимо:
-
сократить время
выполнения каждой работы на критическом
пути; -
сократить время
выполнения одной работы на критическом
пути; -
сократить время
выполнения каждой работы проекта; -
сократить время
выполнения одной работы проекта; -
увеличить
длину критического пути. Вопрос
6. Полный
резерв времени выполнения работы равен
разности между:
-
наиболее поздним
и наиболее ранним временем ее начала; -
наиболее ранним
временем ее начала и наиболее ранним
временем ее окончания; -
наиболее поздним
временем ее начала и наиболее поздним
временем ее окончания; -
наиболее ранним
временем ее окончания и наиболее поздним
временем ее начала; -
наиболее поздним
временем ее окончания и наиболее ранним
временем ее начала.
Задачи
Задача
1. Экономический
факультет МГУ разрабатывает новую
программу для повышения квалификации
преподавателей, обучающих количественным
методам анализа экономики. Желательно,
чтобы эту программу можно было реализовать
в наиболее сжатые сроки. Имеются
существенные взаимосвязи между
дисциплинами, которые необходимо
отразить, составляя расписание
занятий. Например, методы управления
проектами PER
Т/ СРМ должны
рассматриваться лишь
после того, как слушатели обсудят
различные аспекты (коммерческие,
финансовые, экономические, технические
и др.) проектного анализа, связанные с
жизненным циклом проекта.
Дисциплины и их
взаимосвязь указаны в следующей таблице:

Найдите
минимальное время, за которое можно
выполнить программу. Вопросы:
-
Какова длина
критического пути? -
Какое количество
дисциплин находится на критическом
пути? -
Каков
резерв времени изучения дисциплины f?
Задача
2. Консалтинговая
компания «Системы управленческих
решений» специализируется на
разработке
систем поддержки проектов. Компания
заключила контракт на разработку
компьютерной системы,
предназначенной для помощи руководству
фирмы при планировании капиталовложений.
Руководитель
проекта разработал следующий перечень
взаимосвязанных работ:
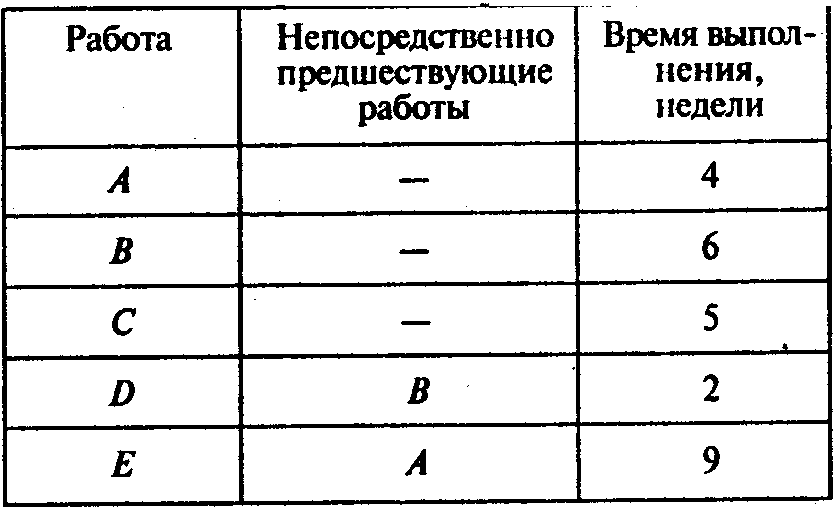
Окончание таблицы
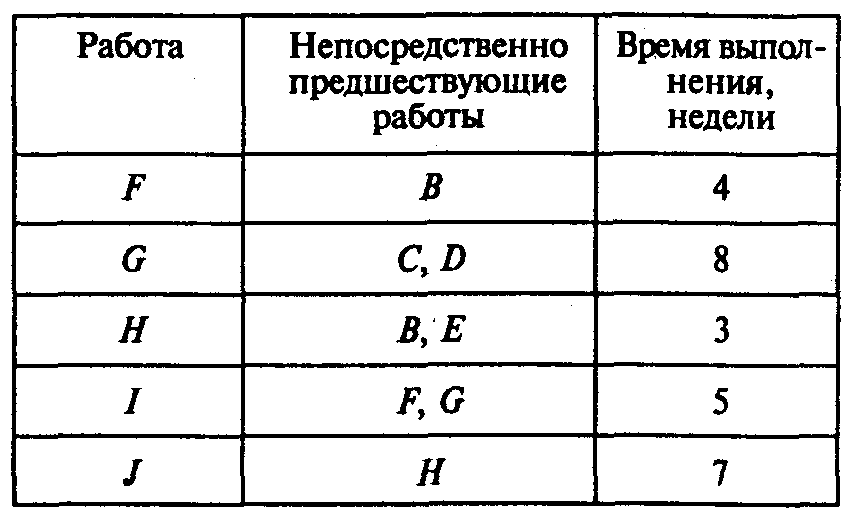
Постройте
графическое представление проекта.
Используйте метод СРМдля
нахождения
критического пути.
Вопросы:
-
Какова длина
критического пути? -
Сколько работ
находится на критическом пути? -
Каков
резерв выполнения работы F?
Задача
3. Рассмотрите
следующий проект:
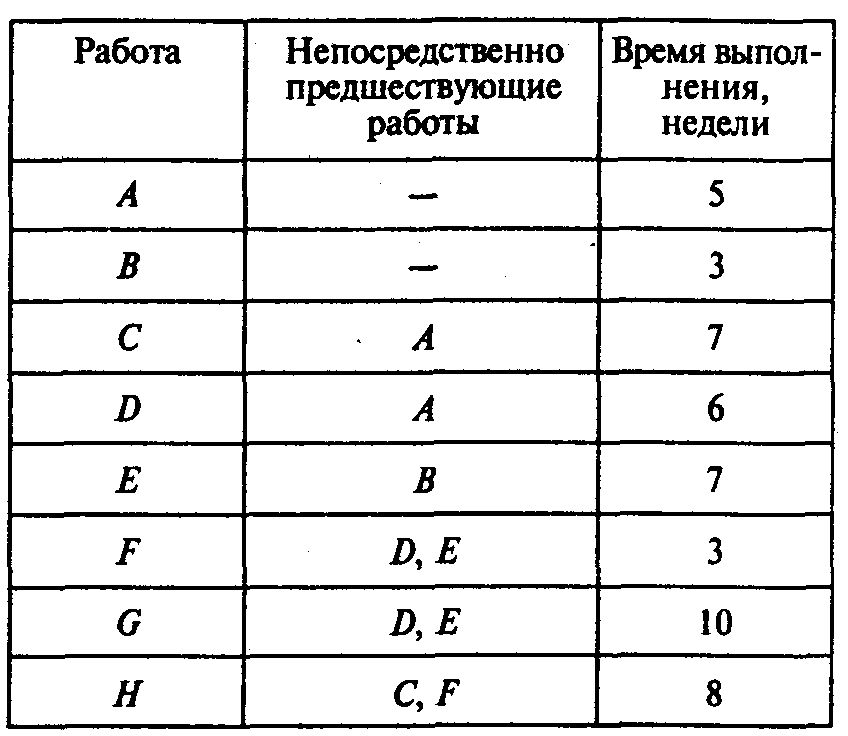
Найдите
критический путь. Вопросы:
-
За какое минимальное
время может быть выполнен проект? -
Сколько работ
находится на критическом пути? -
На
сколько недель можно отложить выполнение
работы D
без
отсрочки завершения проекта в целом? -
На сколько недель
можно отложить выполнение работы С без
отсрочки завершения проекта в целом?
Задача
4. Проект
пусконаладки компьютерной системы
состоит из восьми работ. Непосредственно
предшествующие
работы и продолжительность выполнения
работ указаны в следующей таблице:

Найдите
критический путь. Вопросы:
-
Сколько времени
потребуется для выполнения проекта? -
Сколько работ на
критическом пути? -
Чему
равно наиболее раннее время начала
работы С? -
На
сколько дней можно отложить выполнение
работы С
без
отсрочки завершения проекта в целом?
87
-
Чему
равно наиболее позднее время окончания
работы F? -
На
сколько дней можно отложить выполнение
работы F
без
отсрочки завершения проекта?
Задача
5. Московский
государственный университет рассматривает
предложение о строительстве новой
библиотеки. Работы,
которые следует выполнить перед началом
строительства, представлены ниже:
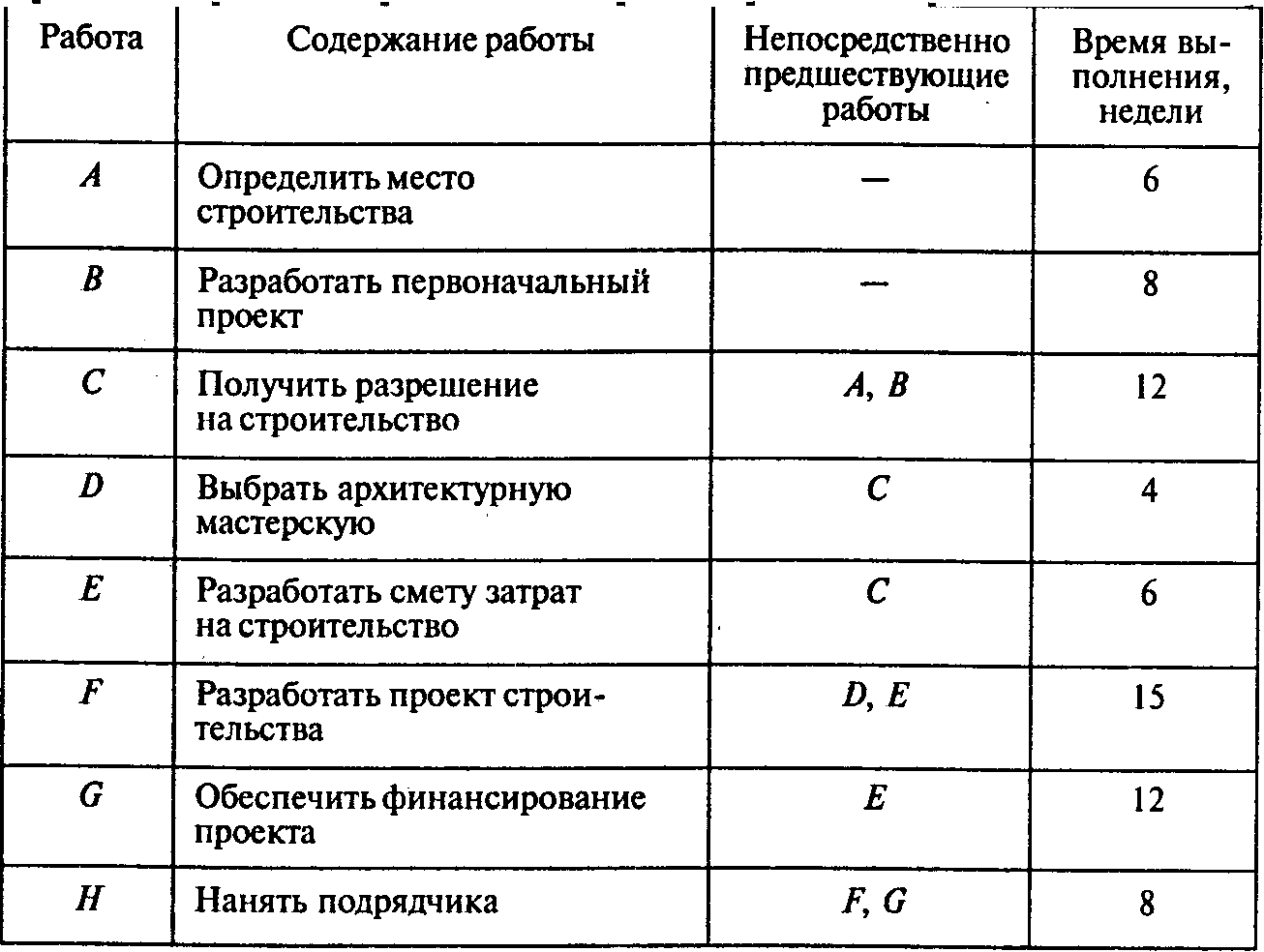
Найдите
критический путь. Вопросы:
-
Сколько работ
находится на критическом пути? (Фиктивные
работы не учитываются.) -
Через какое
минимальное время после принятия
решения о реализации проекта можно
начать работу по строительству
библиотеки? -
На сколько недель
можно отложить выбор архитектурной
мастерской? -
Чему равно наиболее
позднее время завершения работы по
обеспечению финансирования?
5
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ВикиЧтение
Основы управления проектами
Пресняков Василий Федорович
Сокращение времени выполнения проекта
Сокращение времени выполнения проекта
Методы сокращения времени выполнения проекта (операций критического пути) ограничены.
Снижение качества — одна из альтернатив, которая может сократить время выполнения операции на критическом пути.
Заключения контракта на выполнение операции с субподрядчиком. Субподрядчик может иметь доступ к более высоким технологиям или обладать компетентностью, которая может ускорить выполнение операции.
Выделение дополнительных людских ресурсов и оборудования для оставшихся операций. Однако существуют границы того, насколько можно ускорить данное выполнение с помощью дополнительной рабочей силы.
Закон Брукса: дополнительная рабочая сила для опаздывающей программы проекта задержит его выполнение еще больше. Фредерик Брукс сформулировал этот принцип на основе своего опыта руководителя проекта программного обеспечения для IBM System/360 в начале 1960-х.
Последующие исследования показали, что выделение дополнительных людей для опаздывающих проектов всегда приводит к большей стоимости.
Выделение дополнительной рабочей силы на раннем этапе более надежно, чем если это сделать на более позднем этапе, так как новые люди всегда сразу оказывают отрицательное воздействие на ход проекта, на преодоление которого могут потребоваться недели.
Иногда можно изменить логику сетевого графика проекта таким образом, чтобы критические операции осуществлялись параллельно (одновременно), а не последовательно.
Наконец, еще одним методом выполнения работ в срок является сокращение размеров проекта.
Фирмы, занимающиеся программным обеспечением, выпускают продукты, которые не соответствуют первоначальным спецификациям, чтобы потом добавить недостающие характеристики последующим версиям.
Если исключить все эти альтернативы, сокращение времени проекта сводится к сокращению времени конкретной, критической операции для сокращения времени проекта. Эта альтернатива означает появление дополнительных затрат, чтобы сократить время выполнения операции.
Читайте также
Ошибка № 1: Для выполнения задач не отводится конкретного времени и места в расписании
Ошибка № 1: Для выполнения задач не отводится конкретного времени и места в расписании
Одна из самых распространенных причин, по которой вы, возможно, никак не можете приступить к выполнению того, что является для вас важным, состоит в том, что вы не можете отвести или
Ошибка № 3: Вы ошиблись в расчете времени, необходимого для выполнения задач
Ошибка № 3: Вы ошиблись в расчете времени, необходимого для выполнения задач
Большинство людей крайне нереалистично оценивают объем работы, которую они способны выполнить за день. Если время, необходимое для завершения всех запланированных вами дел превышает время,
Вопрос № 2. Сколько времени мне потребуется для выполнения задачи?
Вопрос № 2. Сколько времени мне потребуется для выполнения задачи?
Многие люди никогда не задают себе этот вопрос. Или, возможно, они спрашивают себя, но не знают, как точно оценить время, необходимое для выполнения того или иного дела. Для выполнения одних задач требуется
Расчет времени для выполнения незнакомых задач
Расчет времени для выполнения незнакомых задач
Если у вас прежде не было опыта выполнения какой-либо определенной задачи, особенно, если она достаточно сложна, очень полезно бывает спросить кого-нибудь, кто уже занимался подобными задачами и знает, сколько времени на это
Построение графика стоимости времени выполнения проекта
Построение графика стоимости времени выполнения проекта
При построении графика стоимости времени выполнения проекта необходимо выполнить три следующих основных шага:Найти общие прямые издержки для выбранных продолжительностей проекта. Найти косвенные издержки для
Определение операций для сокращения времени их выполнения
Определение операций для сокращения времени их выполнения
Особую озабоченность вызывает вопрос: продолжительность каких операций сокращать и до какой степени? Общий ответ — критические операции, время выполнения которых можно сократить с наименьшим повышением
Мониторинг времени выполнения работ
Мониторинг времени выполнения работ
Основная цель отслеживания хода работ состоит в том, чтобы как можно раньше заметить отрицательное отклонение от плана и определить, нужны ли корректирующие действия. Основой для сравнения плана с фактическим ходом работ служит
Основания для выполнения проекта
Основания для выполнения проекта
На первый взгляд, причины, по которым вас назначают руководителем проекта (или вы сами беретесь его выполнить), очевидны — так решил ваш шеф. На самом деле вопрос заключается не в том, почему выбрали вас, а в том, почему решили выполнить
Как сократить время выполнения проекта
Как сократить время выполнения проекта
Применение на практике описанных методов покажем на примере нашего пикника. Если вас устраивают 57 минут, чтобы добраться до озера, тогда все в порядке. Но предположим, вы с подругой решили потратить на это не больше 45 минут. Где вы
Аннотация: Процедура сокращения времени.Косвенные издержки проекта. Прямые издержки проекта. Сокращение времени выполнения проекта. Построение графика стоимости времени выполнения проекта. Определение операций для сокращения времени их выполнения. Сценарии управления отклонениями. Манипулирование ресурсами. Увеличение интенсивности работ. Замена исполнителя. Материальное стимулирование. Привлечение субподрядчиков. Манипулирование временем. Изменение сроков завершения работ. Смещение вех. Увеличение общего срока проекта. Манипулирование продуктом (качеством). Снижение качества продукта. Замена продукта. Исключение продукта
Менеджер часто сталкивается с альтернативой, стоит ли сокращение времени на выполнение проекта тех дополнительных расходов, которые связаны с этим.
В ситуациях, связанных с затратами времени, основное внимание сосредоточено на сокращении времени критического пути, который определяет время завершения проекта.
Существует много причин, по которым хотят сократить продолжительность проекта.
Одна из наиболее распространенных причин известна на практике, как «установленное» время продолжительности проекта.
Например, политик публично заявляет, что новая линия метро будет готова через два года.
Или президент компании, занимающейся программным обеспечением, в своей речи заявляет о появлении нового технологически передового программного обеспечения через год.
Очень часто подобные заявления становятся установленными сроками продолжительности проекта, когда не принимаются во внимание затраты, связанные с выполнением проекта в срок.
Время продолжительности проекта устанавливается, когда проект находится еще в стадии «концепции» до или без составления подробного графика всех операций проекта.
Такая практика почти всегда приводит к более высокой стоимости проекта, чем когда мы проводим тщательное планирование.
Но серьезнее всего то, что участники проекта редко распознают или отмечают возросшие затраты из-за установленных сроков.
В последние годы из-за интенсивной глобальной конкуренции и быстрого развития технологий упор делается на своевременную реализацию.
Рынок диктует продолжительность проектов. Например, для фирм со средней или высокой технологиями опоздание на 6 месяцев с доставкой продукта на рынок может привести к огромным потерям прибыли или сокращению доли на рынке примерно на 30%. В этих случаях высокотехнологичные фирмы считают, что экономия времени и сохранение прибыли стоят дополнительных затрат, связанных с сокращением времени без их формального анализа.
Другой причиной сокращения времени проекта могут стать непредвиденные задержки — значительное отставание от графика в середине выполнения проекта. Чтобы снова войти в график, потребуется более сжатое время для выполнения оставшихся критических операций. Дополнительные затраты, связанные с возвращением в график, следует сравнить с затратами, вызванными опозданием.
И, наконец, бывают периоды, когда нужно перераспределить основное оборудование и людей на новые проекты. В этих обстоятельствах стоимость сокращения времени проекта можно сравнить с затратами на выделения основного оборудования или людей.
Процедура сокращения времени
Объяснение издержек проекта
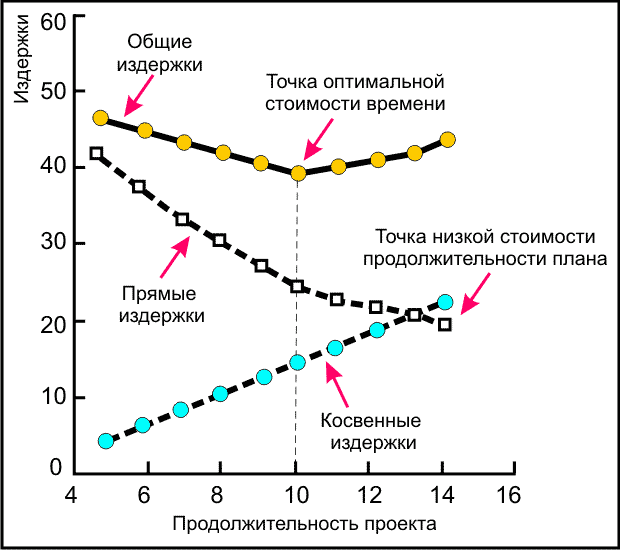
Общий характер издержек проекта показан на рис. 4.1.
Общая стоимость для каждой продолжительности проекта является суммой косвенных и прямых издержек.
Косвенные издержки присутствуют в течение всего времени существования проекта. Следовательно, любое сокращение продолжительности проекта означает сокращение косвенных издержек.
Прямые издержки на графике увеличиваются по мере сокращения продолжительности проекта по сравнению с запланированной продолжительностью.
Имея представленную на графике информацию, менеджеры могут быстро выбрать такую альтернативу, как своевременный выход на рынок.
Рис.
4.1.
График стоимости времени выполнения проекта
Косвенные издержки проекта. Косвенные издержки обычно представляют собой накладные расходы такие, как контроль, администрирование и консультирование.
Косвенные издержки изменяются непосредственно со временем. То есть, любое сокращение времени должно привести к сокращению косвенных издержек.
Если косвенные издержки составляют значительный процент от общих издержек проекта, сокращение времени проекта может представлять весьма существенную экономию (принимая во внимание то, что косвенные ресурсы могут использоваться везде).
Прямые издержки проекта. Прямые издержки обычно связаны с рабочей силой, материалами, оборудованием и иногда с субподрядчиками.
Издержки на установленную продолжительность будут выше, чем для проекта, продолжительность которого разработана из идеальных обычных сроков для операций.
Предполагается, что если прямые издержки рассчитываются, исходя из стандартных методов и времени, то любое сокращение времени операции должно увеличивать издержки на операцию.
При составлении графика, подобного графику на рис. 4.1, необходимо рассчитать прямые затраты, связанные с сокращением времени отдельной критической операции, и затем найти общие прямые издержки для каждой продолжительности проекта, так как время проекта сокращается; процесс требует выбора тех критических операций, сокращение времени которых обойдется дешевле.
Сокращение времени выполнения проекта
Методы сокращения времени выполнения проекта (операций критического пути) ограничены.
Снижение качества — одна из альтернатив, которая может сократить время выполнения операции на критическом пути.
Заключение контракта на выполнение операции с субподрядчиком. Субподрядчик может иметь доступ к более высоким технологиям или обладать компетентностью, которая может ускорить выполнение операции.
Выделение дополнительных людских ресурсов и оборудования для оставшихся операций. Однако существуют границы того, насколько можно ускорить данное выполнение с помощью дополнительной рабочей силы.
Закон Брукса: дополнительная рабочая сила для опаздывающей программы проекта задержит его выполнение еще больше. Фредерик Брукс сформулировал этот принцип на основе своего опыта руководителя проекта программного обеспечения для IBM System/360 в начале 1960-х.
Последующие исследования показали, что выделение дополнительных людей для опаздывающих проектов всегда приводит к большей стоимости.
Выделение дополнительной рабочей силы на раннем этапе более надежно, чем если это сделать на более позднем этапе, так как новые люди всегда сразу оказывают отрицательное воздействие на ход проекта, на преодоление которого могут потребоваться недели.
Иногда можно изменить логику сетевого графика проекта таким образом, чтобы критические операции осуществлялись параллельно (одновременно), а не последовательно.
Наконец, еще одним методом выполнения работ в срок является сокращение размеров проекта.
Фирмы, занимающиеся программным обеспечением, выпускают продукты, которые не соответствуют первоначальным спецификациям, чтобы потом добавить недостающие характеристики последующим версиям.
Если исключить все эти альтернативы, сокращение времени проекта сводится к сокращению времени конкретной, критической операции для сокращения времени проекта. Эта альтернатива означает появление дополнительных затрат, чтобы сократить время выполнения операции.
Построение графика стоимости времени выполнения проекта
При построении графика стоимости времени выполнения проекта необходимо выполнить три следующих основных шага:
- Найти общие прямые издержки для выбранных продолжительностей проекта.
- Найти косвенные издержки для выбранных продолжительностей выбранного проекта.
- Суммировать прямые и косвенные издержки для выбранных продолжительностей .
Затем используется график для сравнения стоимости дополнительных альтернатив и преимуществ. Далее дается подробное описание этих шагов.
Определение операций для сокращения времени их выполнения
Особую озабоченность вызывает вопрос: продолжительность каких операций сокращать и до какой степени?
Общий ответ — критические операции, время выполнения которых можно сократить с наименьшим повышением стоимости на единицу времени.
Сокращение времени выполнения операции называется авралом (crashing).
Кратчайшее время, за которое операция реально может быть выполнена, называется ее предельным временем (crash time).
Прямые затраты на выполнение операции в ее предельные сроки называются стоимостью срочной операции.
Информацию об обычном и предельном времени получают от персонала, знакомого с выполнением операции.
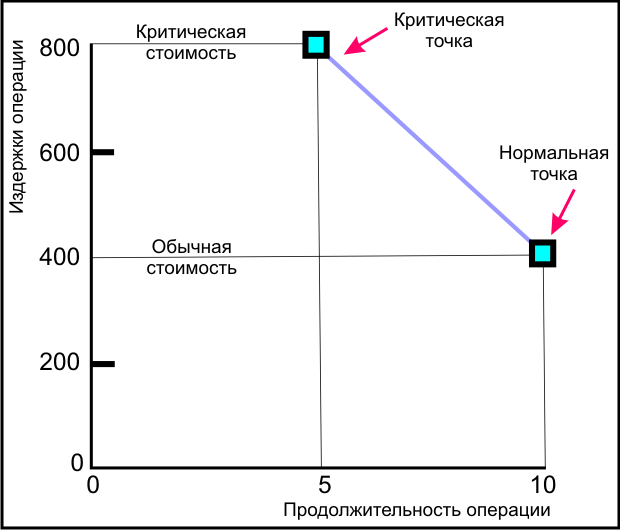
На рис. 4.2 изображен график стоимости времени выполнения гипотетической операции.
Рис.
4.2.
График стоимости времени выполнения операции
Обычное время выполнения операции — 10 единиц и соответствующая стоимость — $ 400. Предельное время выполнения операции — 5 единиц и стоимость — $ 800.
Пересечение обычного времени и стоимости представляет начальную низкую стоимость и раннее начало выполнения графика.
Жирная линия, соединяющая точки обычного и предельного времени, представляет наклонную, что предполагает, что затраты на сокращение времени операции постоянны в единицу времени.
Предположения, лежащие в основе использования этого графика, следующие:
- Отношения стоимости ко времени — линейные.
- Обычное время предполагает низкую стоимость, эффективные методы для завершения операции.
- Предельное время представляет лимит — наиболее возможное сокращение времени в реальных условиях.
- Наклонная линия представляет затраты в единицу времени.
- Все ускорения должны происходить в рамках обычного и предельного времени.
Знание угла наклона операций позволяет менеджерам сравнить и выбрать критические операции, время выполнения которых можно сократить.
Чем меньше угол наклона операции, тем меньше издержки на сокращение периода времени;
Более крутая наклонная означает, что потребуется больше средств на сокращение одной единицы времени.
Стоимость одной единицы времени или наклонной для любой операции рассчитывается по следующему уравнению;
Сравнение наклонных всех критических операций позволяет нам определить, какие операции нужно сокращать, чтобы минимизировать общие прямые издержки.
Имея предварительный график проекта (или тот, который уже в работе), со всеми операциями и их ранним временем начала, можно приступить к процессу поиска критических операций, время выполнения которых можно сократить.
Оптимизация сетевого графика
Оптимизация сетевого графика проводится по времени и ресурсам. Цель оптимизации по времени – сократить продолжительность критического пути. Цель оптимизации по ресурсам – выровнять загрузку исполнителей и сократить численность занятых.
На практике оптимизация сетевого графика проводится чаще всего по времени, чтобы сократить продолжительность разработки в целом, или уложиться в установленные сроки. При этом надо учитывать коэффициенты напряженности путей. Работы, лежащие на путях с коэффициентом напряженности 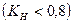
Оптимизация сетевого графика проводится:
– путем изменения схемы сетевого графика, в частности, разделение продолжительной работы на несколько работ, выполняемых параллельно;
– путем перевода части исполнителей с ненапряженных работ, то есть имеющих частные резервы времени, на работы критического пути, выполняемые параллельно с ненапряженными работами. При переводе исполнителей должны быть учтены их квалификация и специальность;
– путем изменения сроков начала и окончания работ ненапряженных путей в пределах их полного резерва времени.
Оптимизация сетевого графика включает следующие этапы:
1. Определяется объем ненапряженной работы (чел-дней), с которой предполагается перевести часть исполнителей на работу критического пути по формуле:
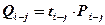
где 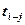
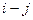
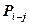
2. Определяется оптимальная численность исполнителей для выполнения данной работы при условии увеличения ее продолжительности на величину частного резерва времени по формуле:
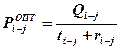
где 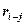
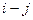
3. Определяется количество исполнителей, которые могут быть переведены на параллельно выполняемую работу критического пути по формуле:
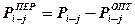
4. Определяется объем работы критического пути, на которую предполагается перевести часть исполнителей, по формуле:
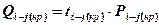
5. Определяется продолжительность работы критического пути после увеличения численности исполнителей на этой работе, по формуле:
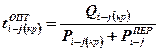
6. Определяется продолжительность критического пути после оптимизации сетевого графика.
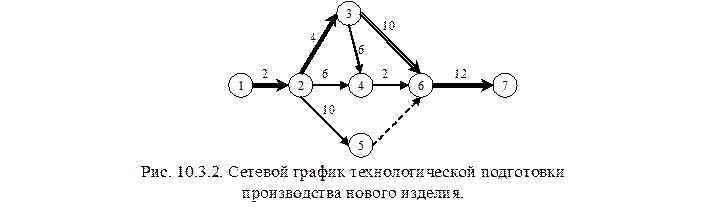
Пример. Разработать и оптимизировать сетевой график по технологической подготовке производства нового изделия, согласно приведенным данным в табл. 10.3.1.
Оптимизация сетевого графика
| № | Наименование работ | Код работы | Продолжительность работы, дни | Количество исполнителей | Специальность |
| 1. | Отработка конструкции на технологичность | 1-2 | Технолог | ||
| 2. | Разработка технологии кузнечно-штамповочного производства | 2-3 | Технолог | ||
| 3. | Разработка технологии литейного производства | 2-4 | Технолог | ||
| 4. | Разработка технологии механической обработки | 2-5 | Технолог | ||
| 5. | Разработка технологии сборки | 3-4 | Технолог | ||
| 6. | Проектирование кузнечной оснастки | 3-6 | Конструктор | ||
| 7. | Проектирование литейной оснастки | 4-6 | Конструктор | ||
| 8. | Фиктивная работа | 5-6 | – | ||
| 9. | Проектирование оснастки для механической обработки | 6-7 | Конструктор |
По приведенным данным строится сетевой график технологической подготовки производства (рис. 10.3.2.).
Расчет основных параметров сетевого графика сводим в таблицу 10.3.2.
Расчет основных параметров сетевого графика
| № | Код работы | 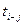 |
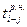 |
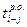 |
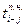 |
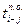 |
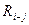 |
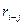 |
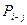 |
| 1-2 | |||||||||
| 2-3 | |||||||||
| 2-4 | |||||||||
| 2-5 | |||||||||
| 3-4 | |||||||||
| 3-6 | |||||||||
| 4-6 | |||||||||
| 5-6 | |||||||||
| 6-7 |
Длина критического пути составит:
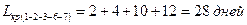
Частными резервами времени располагают работы: 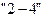
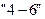
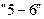
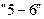
Продолжительность пути, по которому проходят работы, имеющие частные резервы времени, составит:
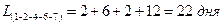
Коэффициент напряженности для данного пути составит:
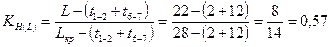
Так как коэффициент напряженности 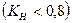
Наибольшим резервом времени имеет работа 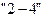
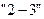
Оптимизацию сетевого графика проводим в следующей последовательности:
1. Определяем объем работы 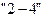
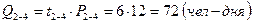
2. Определяем оптимальную численность исполнителей на данной работе:
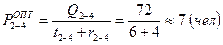
3. Определяем количество исполнителей, которых можно перевести на работу 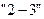
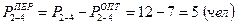
4. Определяем объем работы 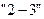
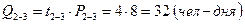
5. Определяем продолжительность работы 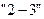
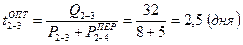
6. Определяем продолжительность критического пути после оптимизации сетевого графика:
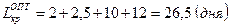
Проверяем продолжительность пути 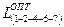
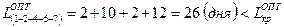
Коэффициент напряженности работ данного пути после оптимизации составит:
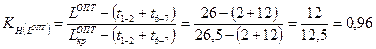
Так как 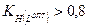
Таким образом, проведя оптимизацию сетевого графика, продолжительность технологической подготовки производства нового изделия сократилась с 28 до 26,5 дня, т. е. на 1,5 дня.
Источник
Методы оптимизации сетевого графика



После того как сетевой график построен и рассчитаны его основные параметры, приступают к его оптимизации. Оптимизация сетевого графика может заключаться либо в сокращении продолжительности критического пути, либо в сокращении ресурсов, необходимых для выполнения всего комплекса работ сетевого графика без изменения его продолжительности.
Вначале рассмотрим анализ и оптимизацию календарных сетей, т.е. тех, в которых заданы только оценки продолжительности работ.
Анализ сетевого графика начинается с анализа топологии сети, включающего контроль построения сетевого графика, установление целесообразности выбора работ, степени их расчленения.
Затем проводятся классификация и группировка работ по величинам резервов. Необходимо отметить, что величина полного резерва времени далеко не всегда может достаточно точно характеризовать, насколько напряженным является выполнение той или иной работы некритического пути. Все зависит от того, на какую последовательность работ распространяется вычисленный резерв, какова продолжительность этой последовательности.
Оценить степень трудности своевременного выполнения всех работ, а также отдельных «цепочек» пути можно с помощью коэффициента напряженности работ.
Коэффициентом напряженности Кн работы (i, j) называется отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим – критический путь.
Коэффициент напряженности вычисляется по следующей формуле:
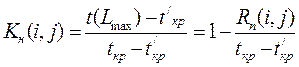
где t (Lmax) — продолжительность максимального пути, проходящего через работу (i,j);
tкр – продолжительность критического пути;
t / кр — продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем;
Rп (i, j) – полный резерв времени работы (i, j).
Коэффициент напряженности изменяется от нуля (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до единицы (для работ критического пути). Причем, чем ближе он к единице, тем сложнее выполнить данную работу в установленный срок.
Найдем коэффициент напряженности работы (3,6) для сетевого графика (рис. 5.2). Ранее мы установили, что продолжительность критического пути tкр = 69 (суток). Далее необходимо определить продолжительность максимального пути (отличного от критического), проходящего через работу (3,6). Такой путь включает в себя события 1 → 2 → 3 → 6 → 7 → 8 → 9 → 10 → 11 → 12 и имеет продолжительность t (Lmax) = 46 (суток). Максимальный путь совпадает с критическим на отрезке 6 → 7 → 8 → 9 → 10 → 11 → 12 продолжительностью t / кр = 4 + 4 + 2 + 10 + 12 + 5 = 37 (суток). Используя формулу (5.10), получим
В соответствии со значениями коэффициента напряженности все работы сетевого графика можно разделить на три группы:
— подкритические (0,6 
2) изменения топологии сети в результате внедрения новой технологии производства работ, позволяющей находить новые последовательности и взаимосвязи работ;
3) расчленения длительных работ на отдельные части и замены последовательных работ параллельными.
Перераспределение ресурсов как инструмент оптимизации сетевого графика предполагает перемещение между работами как трудовых ресурсов, так и техники. При перераспределении трудовых ресурсов необходимо соблюдать ряд правил, в частности: 1) работы, по которым осуществляется перераспределение, должны выполняться в один и тот же период времени; 2) перераспределять ресурсы возможно только на равнокачественных работах, т.е. таких, которые требуют работников одной и той же или взаимозаменяемой профессии и квалификации; 3) перераспределять ресурсы необходимо по величине их убывания в работы с наибольшим дефицитом ресурсов.
В процессе сокращения продолжительности работ критический путь может измениться и в дальнейшем процесс оптимизации будет направлен на сокращение продолжительности работ нового критического пути. И так будет продолжаться до получения удовлетворительного результата. В идеале длина любого из полных путей может стать равной длине критического пути или, по крайней мере, пути критической зоны. Тогда все работы будут вестись с равным напряжением, а срок завершения проекта существенно сократится.
До сих пор мы говорили лишь о соблюдении плановых сроков выполнения комплекса работ, не затрагивая вопросов стоимости разработки проектов. Однако на практике при попытках эффективного улучшения составленного плана неизбежно введение дополнительного к оценкам сроков фактора стоимости работ. Поэтому далее рассмотрим оптимизацию сетевого графика методом «время/стоимость».
Оптимизация сетевого графика в зависимости от полноты решаемых задач может быть условно разделена на частную и комплексную. Разновидностями частной оптимизации сетевого графика являются: минимизация времени выполнения комплекса работ при заданной его стоимости; минимизация стоимости комплекса работ при заданном времени выполнения проекта.
Комплексная оптимизация представляет собой нахождение оптимального соотношения величин стоимости и сроков выполнения проекта в зависимости от конкретных целей, ставящихся при его реализации.
При использовании метода «время-стоимость» предполагают, что уменьшение продолжительности работы пропорционально возрастанию ее стоимости. Каждая работа (i, j) характеризуется продолжительностью t (i, j), которая может находиться в пределах
a (i, j) ≤ t (i, j) ≤ b (i, j), (5.11)
где b (i, j) – нормальная продолжительность выполнения работы (i, j); a (i, j) – минимально возможная (экстренная) продолжительность работы (i, j), которую только можно осуществить в условиях разработки.
При этом стоимость с (i, j) работы (i, j) заключена в границах от сmin (i, j) (при нормальной продолжительности работы) до сmax (i, j) (при экстренной продолжительности работы).
Используя аппроксимацию по прямой (рис. 5.6), можно легко найти изменение стоимости работы ∆с (i, j) при сокращении ее продолжительности на величину
∆с (i, j) = [ b (i, j) – t (i, j)]h (i, j). (5.12)
Величина h (i, j), равная тангенсу угла α наклона аппроксимирующей прямой, показывает затраты на ускорение работы (i, j) (по сравнению с нормальной продолжительностью) на единицу времени:
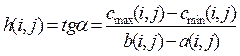
Самый очевидный вариант частной оптимизации сетевого графика с учетом стоимости предполагает использование резервов времени работ. Продолжительность каждой работы, имеющей резерв времени, увеличивают до тех пор, пока не будет исчерпан этот резерв или пока не будет достигнуто верхнее значение продолжительности b (i, j). При этом стоимость выполнения проекта, равная до оптимизации
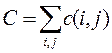
уменьшается на величину
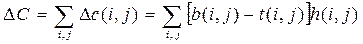







 |
Продолжитель-ность работы
cmin (i,j)
Рис. 5.6. Зависимость стоимости работы от ее продолжительности
После сокращения критического пути за счет проведениятех или иных мероприятий необходимо заново пересчитать сетевой график, чтобы выявить достаточность принятых мер и проверить, не появились ли новые критические пути.
Источник