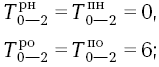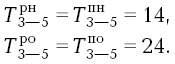Главная / Офисные технологии /
Управление проектами средствами Microsoft Project / Тест 2
Упражнение 1:
Номер 1
Сетевой график – это
Ответ:
(1) ориентированный граф, в котором дугами обозначены работы проекта, а вершинами – временные взаимосвязи работ
(2) ориентированный граф, в котором вершинами обозначены работы проекта, а дугами – временные взаимосвязи работ
(3) ориентированный граф, в котором вершинами обозначены переходы между работами проекта, а дугами – процесс выполнения работ
(4) ориентированный граф, в котором вершинами обозначены работы проекта, а дугами – временные резервы работ
Номер 2
К свойствам сетевого графика относятся:
Ответ:
(1) каждой работе соответствует одна и только одна вершина
(2) ни одна работа не может быть начата до того, как закончатся все непосредственно предшествующие ей работы
(3) одна и та же работа может быть отображена несколькими вершинами
(4) работа может начинаться с опережением, до момента окончания всех предшествующих ей работ
Номер 3
К свойствам сетевого графика относятся:
Ответ:
(1) начало и конец проекта обозначены маркером начала и конца
(2) любая работа, которая непосредственно следует за некоторой работой, может начаться до момента её окончания
(3) ни одна работа, которая непосредственно следует за некоторой работой, не может начаться до момента её окончания
(4) начало и конец проекта обозначены работами с нулевой продолжительностью
Номер 4
Веха используется для
Ответ:
(1) обозначения начала или конца наиболее важных этапов проекта
(2) обозначения работ критического пути
(3) обозначения необязательных работ
(4) обозначения обязательных работ
Упражнение 2:
Номер 1
Критической называется работа
Ответ:
(1) для которой задержка её начала приведёт к задержке срока окончания проекта в целом
(2) для выполнения которой не достаточно трудовых или материальных ресурсов
(3) которая должна быть выполнена сторонней организацией
(4) имеющая самую большую длительность
Номер 2
Критической называется работа
Ответ:
(1) которая является обязательной
(2) которая не является обязательной
(3) не имеющая резерва времени
Номер 3
Критический путь – это
Ответ:
(1) путь от начальной к конечной вершине сетевого графика, проходящий только через критические работы
(2) путь, суммарная длительность работ которого определяет минимальное время реализации проекта
(3) путь, включающий все обязательные работы проекта
(4) путь, проходящий через работы с нулевым резервом времени
(5) путь, включающий в себя все вехи проекта
Номер 4
Нахождение критического пути включает в себя следующие этапы:
Ответ:
(1) вычисление раннего времени начала каждой работы проекта
(2) вычисление позднего времени начала каждой работы проекта
(3) вычисление раннего времени окончания каждой работы проекта
(4) вычисление позднего времени окончания каждой работы проекта
Упражнение 3:
Номер 1
Для вычисления раннего времени начала работ используется следующая формула или схема:
Ответ:
(1) 
(2) 
(3)
T_П(i)=min begin{pmatrix} left(T_П(1)-t_1)\
(T_П(2)-t_2)\
…\
(T_П(n)-t_nright)end{pmatrix}
(4) 
(5)
T_p(i)=max begin{pmatrix} left(T_p(1)+t_1)\
(T_p(2)+t_2)\
…\
(T_p(n)+t_nright)end{pmatrix}
Номер 2
Для вычисления позднего времени начала работ используется следующая формула или схема:
Ответ:
(1) 
(2)
T_p(i)=max begin{pmatrix} left(T_p(1)+t_1)\
(T_p(2)+t_2)\
…\
(T_p(n)+t_nright)end{pmatrix}
(3) 
(4)
T_П(i)=min begin{pmatrix} left(T_П(1)-t_1)\
(T_П(2)-t_2)\
…\
(T_П(n)-t_nright)end{pmatrix}
(5) 
(6) 
Номер 3
Для вычисления резерва времени работы используется формула:
Ответ:
(1) R(i)= TР(i)- TП(i)
(2) R(i)= TП(i)- TР(i)
(3) R(i)=min( TП(i)- TР(i), TР(i)- TП(i))
(4) R(i)=max( TП(i)- TР(i), TР(i)- TП(i))
Номер 4
Для вычисления раннего времени начала работ не используется следующая формула или схема:
Ответ:
(1) 
(2)
T_p(i)=max begin{pmatrix} left(T_p(1)+t_1)\
(T_p(2)+t_2)\
…\
(T_p(n)+t_nright)end{pmatrix}
(3) 
(4)
T_П(i)=min begin{pmatrix} left(T_П(1)-t_1)\
(T_П(2)-t_2)\
…\
(T_П(n)-t_n)right)end{pmatrix}
(5) 
(6) 
Номер 5
Для вычисления позднего времени начала работ не используется следующая формула или схема:
Ответ:
(1) 
(2)
T_p(i)=max begin{pmatrix} left(T_p(1)+t_1)\
(T_p(2)+t_2)\
…\
(T_p(n)+t_nright)end{pmatrix}
(3)
T_П(i)=min begin{pmatrix} left(T_П(1)-t_1)\
(T_П(2)-t_2)\
…\
(T_П(n)-t_nright)end{pmatrix}
(4) 
(5) 
Упражнение 4:
Номер 1
Результатом календарного планирования является:
Ответ:
(1) диаграмма Ганта
(2) график загруженности ресурсов
(3) сетевой график работ
(4) план заключения договоров с поставщиками
(5) график распределения бюджета проекта
Номер 2
Диаграмма Ганта отображает следующие параметры проекта:
Ответ:
(1) структуру работ, полученную на основе сетевого графика
(2) состав используемых ресурсов и их распределение между работами
(3) календарные даты, к которым привязываются моменты начала и завершения работ
(4) процент загруженности исполнителей
(5) длительности работ в рабочих днях
(6) раннее время начала каждой работы
(7) позднее время начала каждой работы
Номер 3
По оси ординат графика загруженности ресурсов отображается
Ответ:
(1) суммарный процент загруженности исполнителя по всем задачам проекта, которые он выполняет в текущий момент времени
(2) резерв времени исполнителя
(3) процент рабочего времени, который исполнитель может выделить на выполнение работ проекта
(4) количество работ проекта, в выполнении которых участвует исполнитель
Номер 4
Задачами менеджера при оперативном управлении проектом являются:
Ответ:
(1) отслеживание фактического графика выполнения работ
(2) сравнение фактического графика выполнения работ с плановым
(3) принятие решений по ликвидации наметившихся отклонений от плана
(4) перепланирование проекта в случае значительных отклонений
(5) подбор состава и длительности работ проекта в соответствии с изменившимися условиями
(6) пересмотр утверждённого сетевого графика работ на основе анализа отклонений от плана
(7) пересмотр контрольных сроков выполнения проекта на основании изменившихся условий
Упражнение 5:
Номер 1
Определите, что изображено на рисунках а), б) и в)

Ответ:
(1) а) – сетевой график, б) – диаграмма Ганта, в) – график загрузки ресурсов
(2) а) – диаграмма Ганта, б) – сетевой график, в) – график загрузки ресурсов
(3) в) – диаграмма Ганта, б) – график загрузки ресурсов, а)– сетевой график
(4) а) – сетевой график, б) – график загрузки ресурсов, в) – диаграмма Ганта
Номер 2
Какой параметр сетевого графика вычисляется в данной таблице:
Ответ:
(1) Раннее время начала работ
(2) Позднее время начала работ
(3) Резерв времени работ
(4) Дефицит времени работ
Номер 3
Какой параметр сетевого графика вычисляется в данной таблице:
Ответ:
(1) Раннее время начала работ
(2) Позднее время начала работ
(3) Резерв времени работ
(4) Дефицит времени работ
Упражнение 6:
Номер 1
На рисунке изображен сетевой график работ, а в таблице – длительности работ. Какой из вариантов таблиц содержит верные значения раннего времени начала работ?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 2 | 3 | 3 | 5 | 5 | 8 |
(2)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 3 | 2 | 3 | 6 | 4 | 9 |
(3)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 2 | 3 | 1 | 5 | 5 | 8 |
(4)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 1 | 3 | 1 | 5 | 5 | 8 |
Номер 2
На рисунке изображен сетевой график работ, а в таблице – длительности работ. Какой из вариантов таблиц содержит верные значения раннего времени начала работ?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 3 | 2 | 3 | 6 | 4 | 9 |
(2)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 2 | 3 | 3 | 5 | 5 | 8 |
(3)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 2 | 3 | 1 | 5 | 5 | 8 |
(4)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 1 | 3 | 1 | 5 | 5 | 8 |
Номер 3
На рисунке изображен сетевой график работ, а в таблице – длительности работ. Какой из вариантов таблиц содержит верные значения раннего времени начала работ?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 2 | 3 | 3 | 5 | 5 | 8 |
(2)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 3 | 2 | 3 | 6 | 4 | 9 |
(3)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 2 | 3 | 1 | 5 | 5 | 8 |
(4)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 1 | 3 | 1 | 5 | 5 | 8 |
Номер 4
На рисунке изображен сетевой график работ, а в таблице – длительности работ. Какой из вариантов таблиц содержит верные значения раннего времени начала работ?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 1 | 3 | 1 | 6 | 5 | 9 |
(2)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 3 | 2 | 3 | 6 | 4 | 9 |
(3)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 2 | 3 | 1 | 5 | 5 | 8 |
(4)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Раннее время начала | 0 | 0 | 0 | 0 | 1 | 3 | 1 | 5 | 5 | 8 |
Упражнение 7:
Номер 1
На рисунке изображен сетевой график работ, а в таблице – длительности работ. Какой из вариантов таблиц содержит верные значения позднего времени начала работ?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 2 | 2 | 0 | 3 | 4 | 6 | 6 | 7 | 9 |
(2)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 1 | 0 | 0 | 2 | 3 | 5 | 5 | 6 | 8 |
(3)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 4 | 0 | 0 | 2 | 3 | 5 | 5 | 6 | 8 |
(4)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 1 | 3 | 0 | 2 | 3 | 5 | 5 | 6 | 8 |
Номер 2
На рисунке изображен сетевой график работ, а в таблице – длительности работ. Какой из вариантов таблиц содержит верные значения позднего времени начала работ?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 2 | 2 | 0 | 3 | 4 | 6 | 6 | 7 | 9 |
(2)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 1 | 0 | 0 | 2 | 3 | 5 | 5 | 6 | 8 |
(3)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 4 | 0 | 0 | 2 | 3 | 5 | 5 | 6 | 8 |
(4)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 1 | 3 | 0 | 2 | 3 | 5 | 5 | 6 | 8 |
Номер 3
На рисунке изображен сетевой график работ, а в таблице – длительности работ. Какой из вариантов таблиц содержит верные значения позднего времени начала работ?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 4 | 2 | 2 | 0 | 3 | 4 | 6 | 6 | 7 | 9 |
(2)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 1 | 0 | 0 | 2 | 3 | 5 | 5 | 6 | 8 |
(3)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 4 | 0 | 0 | 2 | 3 | 5 | 5 | 6 | 8 |
(4)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 1 | 3 | 0 | 2 | 3 | 5 | 5 | 6 | 8 |
Номер 4
На рисунке изображен сетевой график работ, а в таблице – длительности работ. Какой из вариантов таблиц содержит верные значения позднего времени начала работ?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 2 | 2 | 0 | 3 | 4 | 6 | 6 | 7 | 9 |
(2)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 1 | 0 | 0 | 2 | 3 | 5 | 5 | 6 | 8 |
(3)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 4 | 0 | 0 | 2 | 3 | 5 | 5 | 6 | 8 |
(4)
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Позднее время начала | 0 | 1 | 3 | 0 | 2 | 3 | 5 | 5 | 6 | 8 |
Упражнение 8:
Номер 1
На рисунке изображен сетевой график работ, а в таблице – длительности работ. Какой из перечисленных путей является критическим?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1) 1, 4, 5, 8, 10
(2) 1, 2, 5, 8, 10
(3) 1, 3, 6, 8, 10
(4) 1, 3, 6, 9, 10
(5) 1, 3, 7, 9, 10
(6) 1, 4, 7, 9, 10
Номер 2
На рисунке изображен сетевой график работ, а в таблице – длительности работ. Какой из перечисленных путей является критическим?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1) 1, 3, 5, 8, 10
(2) 1, 3, 6, 8, 10
(3) 1, 2, 5, 8, 10
(4) 1, 4, 6, 8, 10
(5) 1, 4, 6, 9, 10
(6) 1, 4, 7, 9, 10
Номер 3
На рисунке изображен сетевой график работ, а в таблице – длительности работ. Какой из перечисленных путей является критическим?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1) 1, 2, 7, 9, 10
(2) 1, 3, 5, 8, 10
(3) 1, 3, 9, 10
(4) 1, 4, 6, 8, 10
(5) 1, 4, 6, 9, 10
(6) 1, 4, 7, 9, 1
Номер 4
На рисунке изображен сетевой график работ, а в таблице – длительности работ. Какой из перечисленных путей является критическим?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1) 1, 2, 5, 8, 10
(2) 1, 2, 7, 9, 10
(3) 1, 3, 8, 10
(4) 1, 3, 9, 10
(5) 1, 4, 6, 8, 10
(6) 6: 1, 4, 6, 9, 10
Упражнение 9:
Номер 1
На рисунке изображен сетевой график работ проекта, а в таблице – длительности работ. Начало проекта – 7.12.09 (понедельник). Какой из приведённых календарных планов соответствует данному проекту, если фирма работает по пятидневной рабочей неделе с выходными в субботу и воскресенье?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1) 
(2) 
(3) 
(4) 
Номер 2
На рисунке изображен сетевой график работ проекта, а в таблице – длительности работ. Начало проекта – 7.12.09 (понедельник). Какой из приведённых календарных планов соответствует данному проекту, если фирма работает по пятидневной рабочей неделе с выходными в субботу и воскресенье?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность работы | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1) 
(2) 
(3) 
(4) 
Номер 3
На рисунке изображен сетевой график работ проекта, а в таблице – длительности работ. Начало проекта – 7.12.09 (понедельник). Какой из приведённых календарных планов соответствует данному проекту, если фирма работает по пятидневной рабочей неделе с выходными в субботу и воскресенье?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1) 
(2) 
(3) 
(4) 
Номер 4
На рисунке изображен сетевой график работ проекта, а в таблице – длительности работ. Начало проекта – 7.12.09 (понедельник). Какой из приведённых календарных планов соответствует данному проекту, если фирма работает по пятидневной рабочей неделе с выходными в субботу и воскресенье?
| Работа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Длительность | 0 | 1 | 2 | 3 | 3 | 2 | 1 | 3 | 2 | 0 |
Ответ:
(1) 
(2) 
(3) 
(4) 
Упражнение 10:
Номер 1
На рисунке изображен календарный план проекта, в котором участвуют сотрудники Р1, Р2, Р3 и Р4. В таблице заданы проценты участия сотрудников в работах проекта. Начало проекта – 7.12.09 (понедельник). Какой из приведённых графиков загрузки соответствует сотруднику Р1?
| Работа | Процент участия | |||
|---|---|---|---|---|
| Р1 | Р2 | Р3 | Р4 | |
| 2 | 50% | 50% | ||
| 3 | 50% | 100% | ||
| 4 | 50% | 100% | ||
| 5 | 50% | 50% | 50% | 50% |
| 6 | 100% | 100% | ||
| 7 | 100% | 100% | ||
| 8 | 100% | 100% | 100% | 100% |
| 9 | 100% | 100% | 50% |
Ответ:
(1) 
(2) 
(3) 
(4) 
Номер 2
На рисунке изображен календарный план проекта, в котором участвуют сотрудники Р1, Р2, Р3 и Р4. В таблице заданы проценты участия сотрудников в работах проекта. Начало проекта – 7.12.09 (понедельник). Какой из приведённых графиков загрузки соответствует сотруднику Р2?
| Работа | Процент участия | |||
|---|---|---|---|---|
| Р1 | Р2 | Р3 | Р4 | |
| 2 | 50% | 50% | ||
| 3 | 50% | 100% | ||
| 4 | 50% | 100% | ||
| 5 | 50% | 50% | 50% | 50% |
| 6 | 100% | 100% | ||
| 7 | 100% | 100% | ||
| 8 | 100% | 100% | 100% | 100% |
| 9 | 100% | 100% | 50% |
Ответ:
(1) 
(2) 
(3) 
(4) 
Номер 3
На рисунке изображен календарный план проекта, в котором участвуют сотрудники Р1, Р2, Р3 и Р4. В таблице заданы проценты участия сотрудников в работах проекта. Начало проекта – 7.12.09 (понедельник). Какой из приведённых графиков загрузки соответствует сотруднику Р4?
| Работа | Процент участия | |||
|---|---|---|---|---|
| Р1 | Р2 | Р3 | Р4 | |
| 2 | 50% | 50% | ||
| 3 | 50% | 100% | ||
| 4 | 50% | 100% | ||
| 5 | 50% | 50% | 50% | 50% |
| 6 | 100% | 100% | ||
| 7 | 100% | 100% | ||
| 8 | 100% | 100% | 100% | 100% |
| 9 | 100% | 100% | 50% |
Ответ:
(1) 
(2) 
(3) 
(4) 
Номер 4
На рисунке изображен календарный план проекта, в котором участвуют сотрудники Р1, Р2, Р3 и Р4. В таблице заданы проценты участия сотрудников в работах проекта. Начало проекта – 7.12.09 (понедельник). Какой из приведённых графиков загрузки соответствует сотруднику Р3?
| Работа | Процент участия | |||
|---|---|---|---|---|
| Р1 | Р2 | Р3 | Р4 | |
| 2 | 50% | 50% | ||
| 3 | 50% | 100% | ||
| 4 | 50% | 100% | ||
| 5 | 50% | 50% | 50% | 50% |
| 6 | 100% | 100% | ||
| 7 | 100% | 100% | ||
| 8 | 100% | 100% | 100% | 100% |
| 9 | 100% | 100% | 50% |
Ответ:
(1) 
(2) 
(3) 
-
Понятие резерва времени работы. Основные виды резервов. Их назначение и использование.
Резерв
времени события показывает, на какое
предельно допустимое время можно
задержать наступление этого события,
не вызывая при этом увеличения времени
комплекса работ.
Для
работ сетевых графиков определяется
два вида резервов времени работ:
-
полный
резерв времени работы Rпij -
свободный
резерв времени работы Rcij
Полный
резерв времени работы показывает,
насколько может быть увеличено время
выполнения этой работы или задержано
начало её выполнения с тем, чтобы
продолжительность max
пути, проходящего через эти работы, не
превысило величины критического пути.
Расчёт полного резерва времени работ
выполняется:
Rпj
= tпj
– tрi
— tij
Свободный
резерв времени соответствует случаю
когда все предшествующие работы
заканчиваются в поздние сроки, а все
последующие начинаются в ранние сроки.
Свободный
резерв времени показывает то максимально
возможное время, на которое можно
увеличить или отсрочить её начало, не
меняя ранних сроков всех последующих
событий, или иначе говория всех последующих
работ.
Свободный
резерв вычисляется по следующей формуле:
Rc
= tpj
– tпi
– tij
-
Полный резерв времени работы. Его назначение. Порядок расчёта и возможности использования.
Полный
резерв времени работы показывает,
насколько может быть увеличено время
выполнения этой работы или задержано
начало её выполнения с тем, чтобы
продолжительность max
пути, проходящего через эти работы, не
превысило величины критического пути.
Расчёт полного резерва времени работ
выполняется:
Rпj
= tпj
– tрi
— tij
Если
снять полный резерв с одной из работ
пути, то он пропадёт и у всех других
работ, это нужно учитывать при оптимизации.
-
Свободный резерв времени работы. Его назначение. Порядок расчёта и возможности использования.
Свободный
резерв времени показывает то максимально
возможное время, на которое можно
увеличить или отсрочить её начало, не
меняя ранних сроков всех последующих
событий, или иначе говория всех последующих
работ.
Свободный
резерв вычисляется по следующей формуле:
Rc
= tpj
– tпi
– tij
-
Цель и содержание анализа и улучшения сетевого графика.
Оптимизацией
часто называют улучшение сетевых
графиков, определяющее, что в отличии
от ЛП, в сетевом планировании оптимизация
ведётся за счёт резерва времени работ,
которые требуют (требует) участия
человека. Которое определяет возможное
использование резервов на работах,
лежащих на критическом пути для сокращения
времени их выполнения(цель типа).
Анализ
сетевого графика заключается в том, что
определяются все возможные резервы
работ и те работы, лежащие на критическом
пути, на которые можно перераспределить
имеющиеся резервы на работах не
критического пути, с целью их возможного
времени выполнения.
-
Возможные подходы к улучшению сетевых графиков. Целесообразные пределы улучшения графиков. Представление графика для последующей работы с ним.
Возможные
подходы к улучшению сетевых графиков:
Оптимизация
ведётся за счёт снятия резервов с
некритичных путей и путём переноса их
на работы критического пути.
Целесообразные
пределы улучшения графиков определяются
тем, что необходимо учитывать возможность
сбоя в работе и необходимость наличия
резерва на данной работе для своевременного
устранения этого сбоя и не допущения
увеличения времени выполнения работ
критического пути, а тем более дальнейшей
невозможности проводить работы. Обычно
не более 50% резерва может быть использовано.
При
улучшении графика с перераспределением
резервов строится новый сетевой график,
заново перерасчитывается, (возможно,
упрощается или усложняется) для
наглядности и простоты последующей
работы с ним.
Фиг
знает чё тут написать…
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение работ, составляющих критический путь, и резервов времени
Критические работы — это работы, которые не имеют никаких резервов времени и должны выполняться точно в заданную временную оценку по каждой работе.
Таким образом, для критических работ будут характерны следующие равенства:
 |
(5) |
или
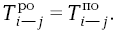 |
(6) |
В нашем сетевом графике эти равенства будут справедливы для работы:
0-2, у которой
2-3, у которой
3-5, у которой
Вводя понятие «путь», мы сравнивали продолжительность всех путей графика и выявляли путь, имеющий наибольшую продолжительность, т.е. критический. Все остальные пути были менее продолжительны, чем критический.
Если из продолжительности критического пути вычесть продолжительность любого другого, то получится полный резерв времени для всего пути.
Вернемся к ранее рассматриваемому сетевому графику.
Определим продолжительность пути, проходящего через события 0-1-3-5. Она будет равна 17. Резерв этого пути будет равен 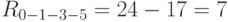
Однако оказывается, что без соответствующей проверки мы не имеем права отнести этот резерв на любую из работ, принадлежащих данному пути, потому что любая из работ может принадлежать одновременно нескольким путям, а не только одному данному пути. Например, работа 0-1. Она принадлежит пяти путям графика. Но если 7 дней мы на нее отнесем полностью, то, например, продолжительность пути 0-1-2-3-5 составит (((7 + 2 + 3 = 12) + 
Значит, мы не имеем права отнести полный резерв пути на любую из работ без соответствующей проверки. Чтобы определить величину резерва для работы 0-1, необходимо рассмотреть все резервы пути, в которые входит эта работа, и взять наименьшую величину резерва. Но это весьма сложно, поэтому есть специальная формула, которая определяет полный резерв времени для каждой работы.
Полный резерв времени для работы (
 |
(7) |
 |
(8) |
Полный резерв времени показывает, что эту работу можно начать позже на величину резерва либо увеличить продолжительность этой работы на величину резерва. При этом конечный срок графика не изменяется. Например, на работе 0-1 полный резерв времени показывает, что эту работу можно начинать не с нуля, а на один день позже или работать не два дня, как это указано в графике, а три дня.
Определим полные резервы времени для всех остальных работ:
Использование полного резерва времени на любой из работ говорит о том, что эта и все остальные работы этого пути (наименьшего) стали работами критическими. Если на работе 0-1 будет использован полный резерв, то изменится раннее начало следующих работ — 1-2 и 1-3, вместо 2 станет 3.
А сохранится ли полный резерв времени на следующий работе 1-2? Нет, так как 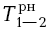

На работе 1-2, как и на работе 0-1 имеется один день полного резерва. Изменится ли раннее начало работ 2-3 и 2-4? Нет, не изменится. У этих работ раннее начало было 6. При использовании полного резерва оно стало 2 + 3 + 1 = 6. Оказывается, на работе 1-2, помимо полного, есть так называемый частный резерв.
Принципиальная разница между полным и частным резервом заключается в том, что использование частного резерва на работе не меняет ранних начал последующих работ.
Частный резерв равен раннему началу последующей работы минус раннее окончание данной работы:
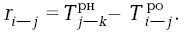 |
(9) |
Используя формулу (9), определим величины частного резерва для работы:
Частный резерв времени показывает, насколько можно увеличить продолжительность работы либо сдвинуть ее раннее начало, не изменяя при этом как раннего начала последующих работ, так и конечного срока графика.
Следует иметь в виду, что величина частного резерва никогда не превышает величину полного резерва времени, а сумма частных резервов всегда равна полному резерву пути.
Расчет резервов времени работ
| № п/п | Работа Рi,j | Продол-житель-ность работы ti,j | Ожидаемое время | Предельное время | Резервы времени работ | |||
| ti | tj | t*i | t*j | 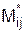
|

|
|||
| А | Б | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0,1 | ||||||||
| 0,3 | ||||||||
| 0,5 | ||||||||
| 1,2 | ||||||||
| 1,4 | ||||||||
| 1,3 | ||||||||
| 2,7 | ||||||||
| 3,4 | ||||||||
| 3,5 | ||||||||
| 3,6 | ||||||||
| 4,7 | ||||||||
| 4,6 | ||||||||
| 5,6 | ||||||||
| 5,8 | ||||||||
| 5,9 | ||||||||
| 6,7 | ||||||||
| 6,10 | ||||||||
| 6,9 | ||||||||
| 6,8 | ||||||||
| 7,10 | ||||||||
| 8,9 | ||||||||
| 9,10 | ||||||||
| 9,11 | ||||||||
| 10,11 |
Пусть требуется оценить вероятность выполнения проекта в директивный срок, равный 63 временным единицам. Для данного сетевого графика дисперсии продолжительности работ критического пути рассчитываются по формуле (3.6); они равны: σ2 (0→3) = 0,1; σ2 (3→5) = 1,8; σ2 (5→6) = 2,8; σ2 (6→9) = 0,1; σ2 (9→10) = 0,1; σ2 (10→11) = 1.
Используя формулы (3.9)–(3.11), получим
Тогда искомая вероятность

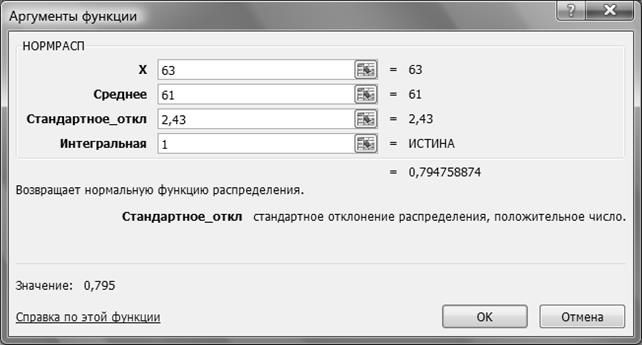
Нормальную функцию распределения можно рассчитать с помощью функции «НОРМРАСП» в среде MS EXCEL. Пример расчета показан на рис. 3.4.
Рис. 3.4 Пример расчета нормальной функции распределения в Excel
Так как значение вероятности составляет 0,8, то с достаточной степенью надежности можно спрогнозировать выполнения проекта в установленный срок (63 временные единицы).
По формуле (3.12) рассчитывается коэффициент сложности сетевого графика:
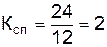
Следовательно, сетевой график средней сложности.
Для заданной работы (например, 1→4) по формуле (3.13) рассчитывается коэффициент напряжённости


Максимальный путь, проходящий через работу 1→4: 0→1→4→6→9→ 10→11, имеет продолжительность t(Lmax) = 49 (временных единиц). Максимальный путь L4 совпадает с критическим (см. рис. 3.2) на отрезке 6→9→ 10→11 продолжительностью t’кр = 13 + 6 + 13 = 32 временные единицы.
Работу 1→4 можно отнести к резервной зоне (Кн i,j < 0,6).
Проведём частную оптимизацию сетевого графика методом «время-стоимость».
Граничные значения продолжительностей работ аij и bij, их стоимости сij, коэффициенты затрат на ускорение работ hi,j приведены в табл. 3.3. Свободные резервы времени работ 
Таблица 3.3
Оптимизация сетевого графика методом «время-стоимость»
| № п/п | Работа, Рi,j | Продолжительность работы | 
|
сi,j | Коэффициент затрат на ускорение работы, hi,j |
Уменьшение удельной стоимости проекта, ΔСij | ||
| ai,i | 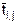
|
bi,i | ||||||
| 0,5 | 5 ∙ 8 = 40 | |||||||
| 1,4 | 4 ∙ 4 = 16 | |||||||
| 1,3 | 1 ∙ 12 = 12 | |||||||
| 2,7 | 4 ∙ 6 = 24 | |||||||
| 3,6 | 3 ∙ 10 = 30 | |||||||
| 4,7 | 2 ∙ 5 = 10 | |||||||
| 4,6 | 3 ∙ 12 = 36 | |||||||
| 5,8 | 7 ∙ 1 = 7 | |||||||
| 5,9 | 6 ∙ 7 = 42 | |||||||
| 6,1 | 5 ∙ 5 = 25 | |||||||
| 7,10 | 10 ∙ 4 = 40 | |||||||
| 8,9 | 1 ∙ 3 = 3 | |||||||
| 9,1 | 2 ∙ 4 = 8 | |||||||
| Итого | – |
В табл. 3.3 представлены параметры лишь тех работ, которые имеют свободный резерв времени. Стоимости ci,j остальных работ: c(0,1) = 50; c(0,3) = 45; c(1,2) = 82; с(3,4) = 55; с(3,5) = 72; с(5,6) = 30; с(6,7) = 26; с(6,9) = 75; с(6,8) = 42; с(9,10) = 35; с(10,11) = 10 (усл. ден. ед.). Подчеркнуты те работы, свободные резервы времени которых полностью использованы на увеличение их продолжительности.
Стоимость первоначального варианта сетевого графика или плана по формуле (3.16) равна сумме стоимостей всех работ (в том числе работ, не имеющих резервов и не включенных в табл. 3.3):
С = 694 + 50 + 45 + 82 + 55 + 72 + 30 + 26 + 75 + 42 + 35 + 10 =
= 1216 усл. ден. ед.
Стоимость нового плана C’ = С – ΔС = 1216 – 293 = 923 усл. ден. ед., т. е. стоимость уменьшилась почти на 25 %.
В результате оптимизации сети получился план, позволяющий выполнить комплекс работ в срок tкр = 61 ед. времени при минимальной его стоимости С = 923 усл. ден. ед.
В реальных условиях выполнения проекта может потребоваться ускорение его выполнения, что, естественно, отразится на стоимости проекта – она увеличится.
3.5. Последовательность решения задачи
Выполнение задачи осуществляется в следующем порядке:
1) постановка задачи (что такое сетевой график, его элементы и правила построения, правила организации работ);
2) составление сетевого графика в соответствии с заданием (по данным о кодах и длительностях работ);
3) расчёт временных параметров сетевого графика (среднего времени выполнения работы, раннего и позднего сорока свершения событий);
4) определение полного и свободного резервов времени выполнения работ;
5) определение критического пути сетевого графика и его выделение на рисунке;
6) оценка вероятности выполнения комплекса работ в установленный срок;
7) расчёт коэффициента сложности сетевого графика и определение коэффициентов напряжённости для заданных работ;

Расчет вариантов должен быть приведен в работе. Таблицы необходимо составлять по предложенной форме.
По результатам работы следует сделать выводы:
1) определить сложность сетевого графика: простой, средней сложности, сложный;
2) в зависимости от коэффициентов напряжённости классифицировать работы по зонам (в соответствии с предложенным вариантом): критическая, подкритическая, резервная;
3) оценить опасность срыва выполнения комплекса работ в установленный директивный срок: высокая, низкая степень вероятности;
4) определить, на сколько процентов уменьшилась стоимость выполнения комплекса работ, в результате оптимизации методом «время-стоимость».
3.6. Исходные данные
Решение задачи осуществляется по вариантам применительно к табл. 3.5, 3.8. Исходная информация, необходимая для решения задачи, приведена в табл. 3.4–3.8.
1. По данным о кодах и длительностях работ необходимо построить график привязки сетевой модели, рассчитать среднее время выполнения работ, временные параметры событий и резервы времени работ. Определяются номера вариантов исходных данных применительно к табл. 3.5 и 3.8 следующим образом. Две последних цифры номера зачетной книжки студента делятся с остатком на количество вариантов, представленных в табл. 3.4. К остатку от деления прибавляется единица. Полученное число явится номером варианта для информации соответствующего вида. Значения длительности и стоимости работ округлять до целых. Увеличивать все (аij, bij, mij, сi,j сi,jmax сi,jmin) показатели. Для табл. 3.6–3.7 варианты рассчитываются отдельно.
Таблица 3.4
|
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм… |
Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени… |
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил… |
Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах… |