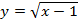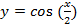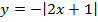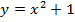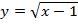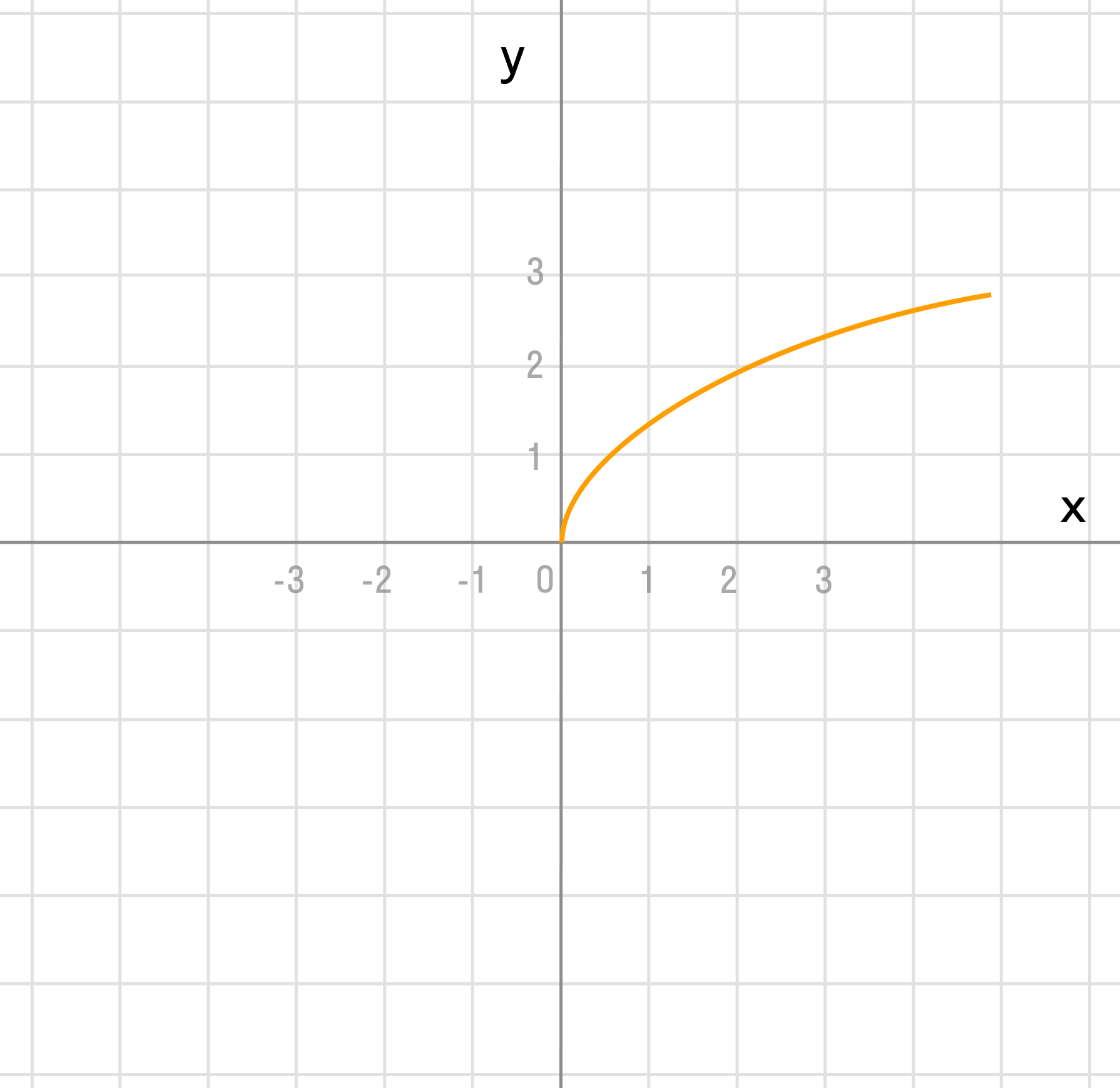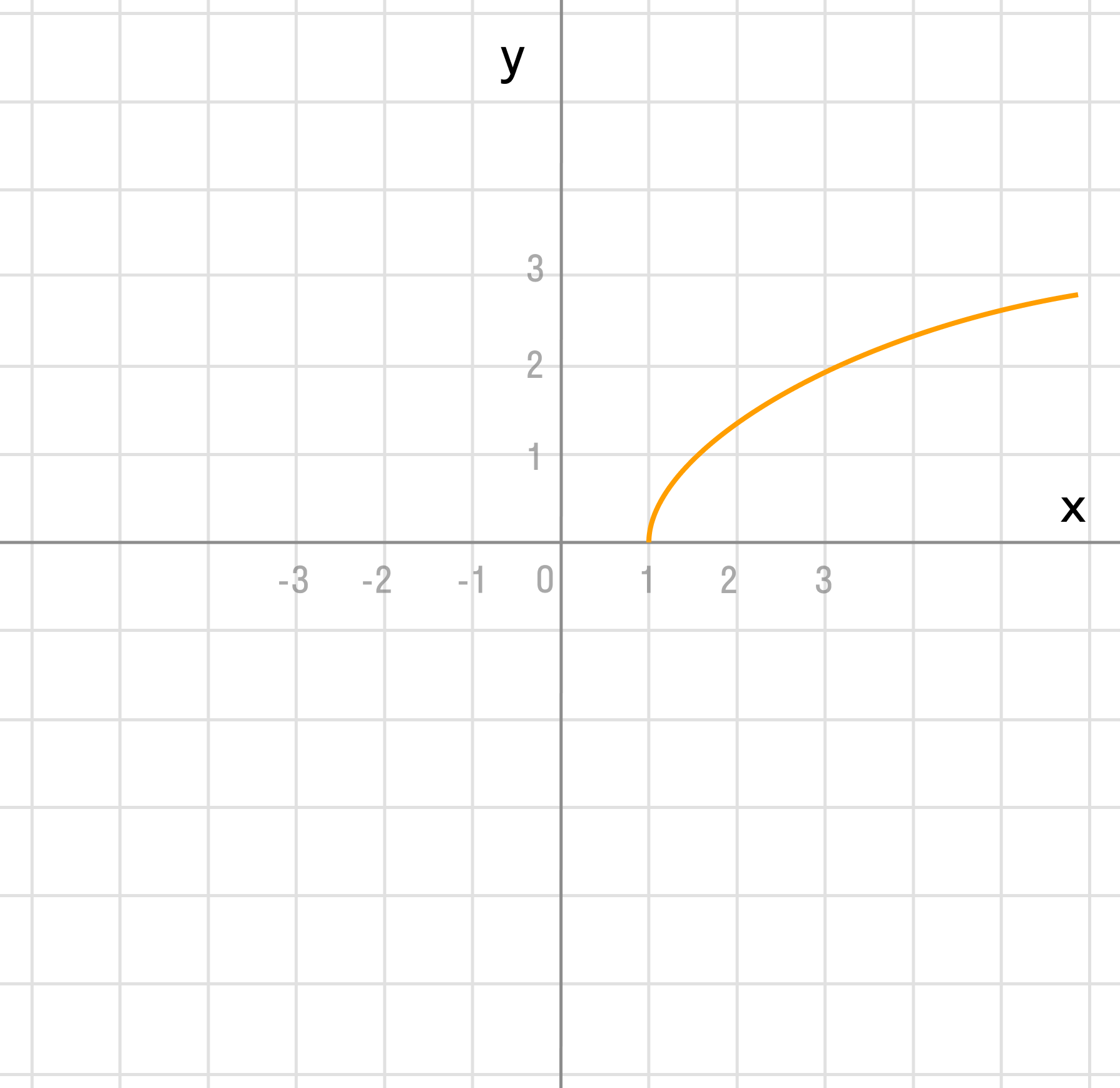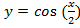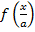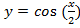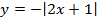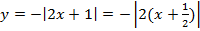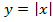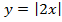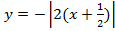Главная
Графиках показано зависимость количества произведенных деталей рабочими А и В от времени. какой …
-
- 0
-
Графиках показано зависимость количества произведенных деталей рабочими А и В от времени. какой из рабочих произвел деталей больше в период 4-го по 7-ой час рабочего времени и На сколько больше?
Роман Шкирков
Вопрос задан 24 сентября 2019 в
5 — 9 классы,
Математика.
-
Комментариев (0)
Добавить
Отмена
1 Ответ (-а, -ов)
- По голосам
- По дате
-
- 0
-
А — 70-50=20(дет.) В — 90-40=50(дет.)
Ответ: рабочий В произвел на 30 деталей больше, чем рабочий А.
Отмена
Елисей Могосов
Отвечено 24 сентября 2019
-
Комментариев (0)
Добавить
Отмена
Ваш ответ
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 4101 Построить график функции y=8/x….
Условие
Banana
16.10.2015
Построить график функции y=8/x.
математика 6-7 класс
44309
Решение
Ответ: В решение
Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,627 -
гуманитарные
33,648 -
юридические
17,917 -
школьный раздел
611,615 -
разное
16,897
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Технологическая карта урока по алгебре для
8 класса на тему «Функция y
= k/x
и ее график»
Цель
урока:
— обучающая: ввести понятие функции
обратная пропорциональность, изучить ее свойства, формировать умение строить
график функции, в том числе, используя СКМ Maxima;
— развивающая: развитие памяти,
логического мышления, способности четко формулировать свои мысли; развитие
навыков работы с системой компьютерной математики; интерес к предмету
математики;
— воспитывающая: развитие кругозора,
воспитание информационной культуры обучающихся, воспитание аккуратности при
построении графиков.
Формируемые
предметные результаты
овладение системой функциональных понятий, функциональным языком и
символикой, умение строить графики функций, описывать их свойства, использовать
функционально-графические представления для описания и анализа математических
задач и реальных зависимостей.
Формируемые метапредметные результаты:
— личностные
универсальные учебные действия: развитие навыка
самостоятельности в работе, самоанализа и самоконтроля при оценке результата и
процесса своей деятельности;
-регулятивные
универсальные учебные действия: вносить
необходимые коррективы в действие после его завершения на основе учета
характера сделанных ошибок;
-познавательные
универсальные учебные действия: проводить
сравнение и классификацию по заданным критериям.
Тип
урока: урок открытия нового знания
Формы
работы учащихся: коллективная, ИКТ,
групповая, метод проблемного вопроса.
Дидактические средства: карточки
с заданиями для групповой работы, листы самооценки, учебник Алгебра.
8 класс: Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович и др. – 5-е изд. – М. :
Просвещение, 2018
Необходимое
техническое оборудование: ПК учителя, интерактивная
доска, проектор, ПК учащихся, программное обеспечение СКМ Maxima.
СТРУКТУРА И ХОД УРОКА
|
Этап урока |
Деятельность учителя |
Деятельность учащихся |
Формируемые УУД |
|||
|
Познавательные |
Регулятивные |
Личностные и коммуникативные |
||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
Организационный |
Приветствие. Напоминает, как заполнять лист |
Вспоминают: «плюс» — справился с заданием, |
Развитие умения организовать рабочую среду |
||
|
2 |
Мотивация учебной деятельности |
Предлагает ответить, какой художественный прием |
Читают выражения на интерактивной доске: «Море слез» «Мы не виделись уже сто лет» «Рос не по дням, а по часам» Отвечают: гипербола. |
Анализ с целью выделения признаков |
Оценивание усваиваемого содержания |
|
|
3 |
Актуализация |
Формулирует задание: 1. Выполните устно 2.Закончите предложения а) С увеличением цены количество товара, данную сумму денег …; б) С уменьшением в) С увеличением количество рабочих …. Вспомните, как |
1. Выполняют задания 2. Отвечают на вопросы: а) уменьшится; б) увеличится в) уменьшится. |
Поиск и выделение необходимой информации |
Контроль и коррекция |
Аргументирование своего мнения, умение корректно |
|
4 |
Постановка учебной задачи. |
Формирует три группы учащихся, раздает карточки с 1. 2. 3. Формулирует задание. Как вы думаете, чем мы будем |
Выражают формулой зависимость между величинами, определяют, |
Формулирование познавательной цели |
Постановка учебной задачи на основе соотнесения |
Умение с точностью выражать свои мысли |
|
5 |
Этап учебных действий. Групповая работа |
Функция обратная пропорциональность является общей |
1 группа строит график зависимости силы тока от wxplot2d(x/(x^2-1), 2 группа — радиуса колеса и числа совершаемых им 3 группа – количество товара на определенную сумму |
Анализ объектов, построение логической цепи |
Планирование, взаимоконтроль, коррекция |
Выражение своих мыслей, аргументация своего мнения, |
|
6 |
Этап учебных действий. Представление результатов |
Предлагает план ответа: 1) какие значения принимают Предлагает проверить, что произойдет с графиком, |
Каждая группа представляет свою работу. Делают wxplot2d([-5/x, |
Проводить сравнение и классификацию по заданным |
Выделение и осознание того, что усвоено и что еще |
Умение с точностью выражать свои мысли |
|
7 |
Этап первичного понимания новых знаний. Работа в парах |
Организует работу с учебником: -знакомит с определением функции обратная — разбирает примеры графиков, стр. 267-268, рис. |
1 ученик пары строит график функции y=12/x? 2 ученик — y=-12/x. |
Построение логической цепи рассуждений, выполнение |
Контроль, коррекция |
Развитие навыка самостоятельности в работе |
|
8 |
Этап первичного контроля новых знаний |
Организует заполнение таблицы «Свойства функции |
Выходят к доске, выбирают из предложенного списка |
Установление причинно-следственных связей, |
Контроль, коррекция, оценка |
Нравственно-этическое оценивание |
|
9 |
Рефлексия |
Подведение итогов урока: Сегодня я узнал… Работа над заданием помогла мне… Меня удивило… У меня появилось желание… Я научился… Я не понял… |
Анализируют свою деятельность на уроке, делают |
Умение проговаривать последовательность действий на |
Осознание качества и уровня усвоения |
Оценивание усвоенного содержания |
|
10 |
Фиксация итогов урока. Домашнее задание. |
Объявляет оценки за активную работу, правильно Информация о домашнем задании размещена на ИД на Это первая часть д/з, а вторая – по учебнику( п. |
Записывают домашнее задание |
ТЕМА 3
Построение диаграмм в среде EXCEL
3.1 Примеры решения задач
Построение графиков
Рассмотрим процесс построения графиков и диаграмм на конкретных примерах.
Упражнение 1. Построить график функции f (t) 65,5 e 0,15 t , если t изменяется от 0 до 15 с шагом 1.
Подготовка данных:
Подпишите (озаглавьте) столбцы.
Введите текст в ячейки: A1 → t, ч; B1 → f(t).
Задайте начальное значение t в ячейке A2: A2 → 0
Задайте формулу изменения переменной (аргумента) в ячейке A3: A3 → = A2+1
Совет: при вводе формулы скопируйте ячейку A2.
Скопируйте содержимое ячейки A3 (формулу) в диапазон ячеек
A4:A17.
Задайте формулу вычисления функции f(t) в ячейке B2: B2 → =65,5*exp(–0,15*A2).
Скопируйте содержимое ячейки B2 (формулу) в диапазон ячеек
B3:B17.
1. Создание графика:
Перед началом построения необходимо указать программе диапазон ячеек с данными, на основании которых должен быть построен график.
Совет. Чтобы на графике отображались и наименования данных, следует выделить также ячейки, которые содержат наименование столбцов.
Выделите ячейки с данными, по которым необходимо построить график. В нашем случае это диапазон ячеек А1:B17.
На вкладке Вставка в группе Диаграммы нажмите кнопку
Точечная (рис. 3.1).
21
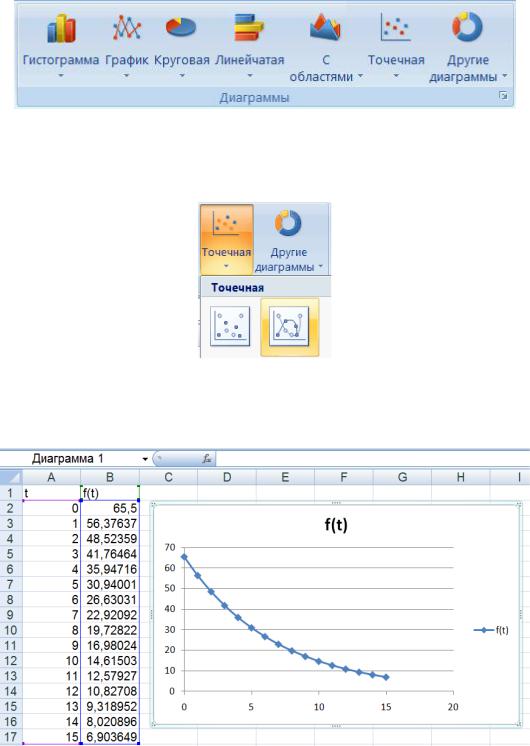
Рисунок 3.1 – Выбор типа диаграммы
Выберите тип диаграммы Точечная с гладкими кривыми и маркерами (рис. 3.2).
Рисунок 3.2 – Выбор типа диаграммы
На рабочем листе будет построен график рис. 3.3.
Рисунок 3.3 – График
2. Форматирование (редактирование) графика:
Созданная диаграмма пока имеет малопривлекательный вид. Наша задача отредактировать ее, сделав более наглядной и информативной.
Щелкните в области диаграммы.
22

Откроется панель Работа с диаграммами с дополнительными вкладками Конструктор, Макет и Формат.
На вкладке Конструктор в группе Стили диаграмм выберите стиль, который хотите использовать.
Для данного графика использовался Стиль 2 (рис. 3.4).
Рисунок 3.4 – Выбор стиля диаграммы
На вкладке Макет в группе Оси нажмите кнопку Сетка и
последовательно выберите Вертикальные линии сетки по основной оси и Основные линии сетки.
Выберите (щелкните) на данных горизонтальной оси. Горизонтальная ось с данными будет выделена. В группе Текущий фрагмент выберите Формат выделенного фрагмента и в открывшемся окне Формат оси задайте необходимые параметры оси (рис. 3.5) и нажмите кнопку Закрыть.
В нашем случае задано – максимальное значение:
фиксированное 15.
Щелкните название диаграммы и введите нужный текст. Для данного графика было задано название График f(t).
Чтобы уменьшить размер шрифта в наименовании диаграммы, щелкните текст правой кнопкой мыши и введите нужный размер в контекстном меню в поле Размер.
Для данного графика был использован размер шрифта 12.
На вкладке Макет в группе Подписи нажмите кнопку Названия осей и выполните действия, описанные ниже.
Чтобы добавить подпись основной вертикальной оси, выделите пункт Название основной вертикальной оси и затем выберите нужный тип названия вертикальной оси.
Для данного графика было выбрано Повернутое название.
Щелкните название, введите нужный текст и нажмите клавишу ENTER. Выполните аналогичные действия для добавления подписи основной горизонтальной оси. Для данного графика были заданы названия: основной вертикальной оси – f(t) и основной горизонтальной оси – t, ч.
На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительно 
23

Для данного графика был выбран Слабый эффект – Темный 1
(рис 3.6).
Рисунок 3.5 – Окно Формат оси
Рисунок 3.6 – Выбор стиля фигур
Щелкните в области графика.
На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительно 
24
Если нужно использовать цвета темы, отличающейся от темы по умолчанию, примененной к книге, выполните указанные ниже действия.
На вкладке Разметка страницы в группе Темы нажмите кнопку
Темы (рис. 3.7).
Выберите нужную тему в разделе Встроенные. Для данного графика была использована Стандартная тема. На рисунке 3.8 показан полученный график.
Рисунок 3.7 – Выбор темы
Рисунок 3.8 – График
ПОСТРОЕНИЕ ГИСТОГРАММЫ
Упражнение 2.
1. Создайте таблицу исходных данных рис. 3.9. Таблица представляет по компонентный состав атмосферы.
25

Рисунок 3.9 – Состав атмосферы
Действия:
Построение гистограммы.
Выделите ячейки с данными, по которым необходимо построить гистограмму. В нашем случае это диапазон ячеек А2:B7 (рис. 3.9).
На вкладке Вставка в группе Диаграммы нажмите кнопку
Гистограмма и выберите Объемная гистограмма с группировкой.
Выполните форматирование гистограммы (см. упр. 1). Примерный вид полученной гистограммы может быть, например,
таким как показан на рис. 3.10.
Рисунок 3.10 – Объемная гистограмма
26

ПОСТРОЕНИЕ КРУГОВОЙ ДИАГРАММЫ.
Выделите ячейки с данными, по которым необходимо построить гистограмму. В нашем случае это диапазон ячеек А2:B7 (рис. 3.10).
На вкладке Вставка в группе Диаграммы нажмите кнопку
Круговая и выберите Объемная разрезная круговая.
Выполните необходимые действия для форматирования гистограммы (см. упр. 1).
Примерный вид полученной гистограммы показан на рис. 3.11.
Рисунок 3.11 – Круговая диаграмма
3.2. Задачи для выполнения лабораторных работ
Задание 1.
Построить график функции в заданном диапазоне, шаг выбрать произвольно.
Таблица 3.1 – Варианты задач
|
Вар. |
Функция |
Диапазон |
|
1. |
Y = 2·x + cos(x) – 0,5 |
– 3,14 < x < 3,14 |
|
2. |
Y = x + ln(x) – 0,8 |
1 < x < 10 |
|
3. |
Y = 2·x – lg(x) – 7 |
2< x < 10 |
|
4. |
Y = (x + 1)0,5 – 1/x |
2 ≤ x < 5 |
27
Окончание таблицы 3.1
|
Вар. |
Функция |
Диапазон |
|
5. |
Y = x2 + 4·sin(x) |
– 3,14 < x < 3,14 |
|
6. |
Y = x + cos(x) – 1 |
1,7 < x < 4,5 |
|
7. |
Y = x3 – sin(x) |
– 3,14 < x < 3,14 |
|
8. |
Y = x·(x + 1)2 – 1 |
0 < x < 10 |
|
9. |
Y =2·x + lg(x)+0,5 |
2 < x < 6 |
|
10. |
Y = sin(x) + cos(x) |
– 3,14 < x < 3,14 |
Задание 2.
1. Построить график зависимости коэффициента трения в трубах от значения критерия Re:
|
= |
0,398 |
для |
3000 Re 16000 |
|
|
Re0,254 |
||||
|
2. |
Построить график зависимости скорости реакции по уравнению |
|||
|
K 78,56e 0,1037 , если |
1 25. |
|||
|
3. |
Построить график зависимости между количеством раствора y – |
(в %), уносимого из выпарного аппарата, и его производительностью x – (в кг/ч) по уравнению:
y 5,789x2,071 10 7 0,048, для 250 x 2000
4. Построить график зависимости между атмосферным давлением p (в мм. рт. ст.) и барометрической высотой h (в км) по уравнению
|
p |
760 10 0,0531h , |
для 0 h 6 |
5. Построить график зависимости содержания влаги, x (в % от веса сухого остатка) от времени t (мин.) по уравнению
|
x |
101,4568 0,00938t , |
для 0 t 100 |
28
6. Построить график зависимости растворимости натриевой соли хлорноватистой кислоты в воде x (в г/100г воды) от температуры t (в 0C) по уравнению
x 7,894e0,1939t 4,82 , для 0 t 60
7. Построить график зависимости процентного содержания воды в смеси эфира с водой x от температуры t (в 0C) по уравнению
x 0,00016t2 0,0143t 0,59, для 0 t 110
8. Построить график зависимости объема воздуха (измеренный при t 0C и 760 мм.рт.ст.) v (в мл.), содержащегося в воде от температуры t C по уравнению
|
v (t 5)/( 1,386 0,0375t) 25,68, |
для 0 t 25 |
9. Построить график изменения температуры воздуха в сушилке T в течение суток по уравнению
|
T |
80 14,99cos(15 37) 18cos(30 353), для |
1 24 |
10. Построить график изменения содержания азота в газе X% от времени пребывания в высокотемпературном реакторе по уравнению
|
X 0,1793ln( ) 0,7724, для |
0,1 0,8 сек. |
29

ТЕМА 4 Работа с таблицами.
4.1. Примеры решения задач
Пример 4.1.
Пусть требуется составить материальный баланс печи для сжигания серы производительностью Q=60т/сутки (60/24=2,5т/ч).
Расчет следует вести на производительность печи по сжигаемой сере, в кг/ч.
Процесс горения серы описывается уравнением реакции: S + O2 = SO2
Данные для расчета:
Производительность печи по сере ….………………2500 кг/ч
Степень окисления серы……………….…………………. 0,95 Коэффициент избытка воздуха………….……………… 1,5
Исходная таблица (все массы и объемы соответствуют массовому и объемному расходам в час)
Рисунок 4.1 – Таблица исходных данных для расчета материального баланса
Последовательность расчета:
1)Определение количества серы, вступившего в реакцию
E4=C4*B4
2)Определение количества серы, не вступившего в реакцию
F4=C4–E4
Определение массы кислорода для окисления серы; MmS=32, MmO2=32
30
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Понятие функции
Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие значения функции. Вот, какими способами ее можно задать:
-
Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
-
Графический способ — наглядно.
-
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
-
Словесный способ.
Область определения функции — это множество всех допустимых значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Например, для функции вида
область определения выглядит так
-
х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): (-∞; 0) ⋃ (0; +∞).
Область значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): [0; +∞).
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
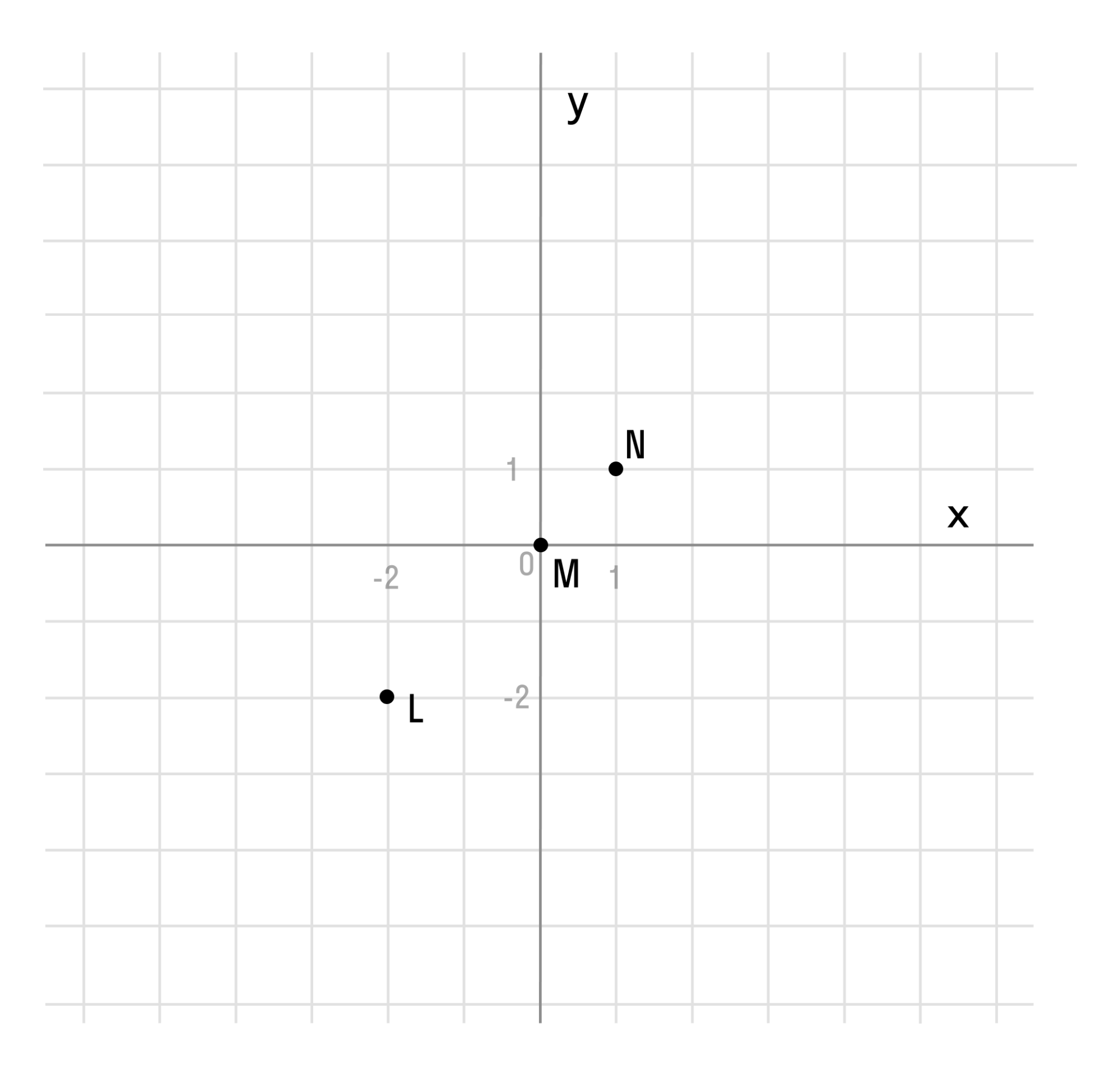
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться при решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Запоминаем!
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.
Исследование функции
Важные точки графика функции y = f(x):
-
стационарные и критические точки;
-
точки экстремума;
-
нули функции;
-
точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых значение функции равно нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
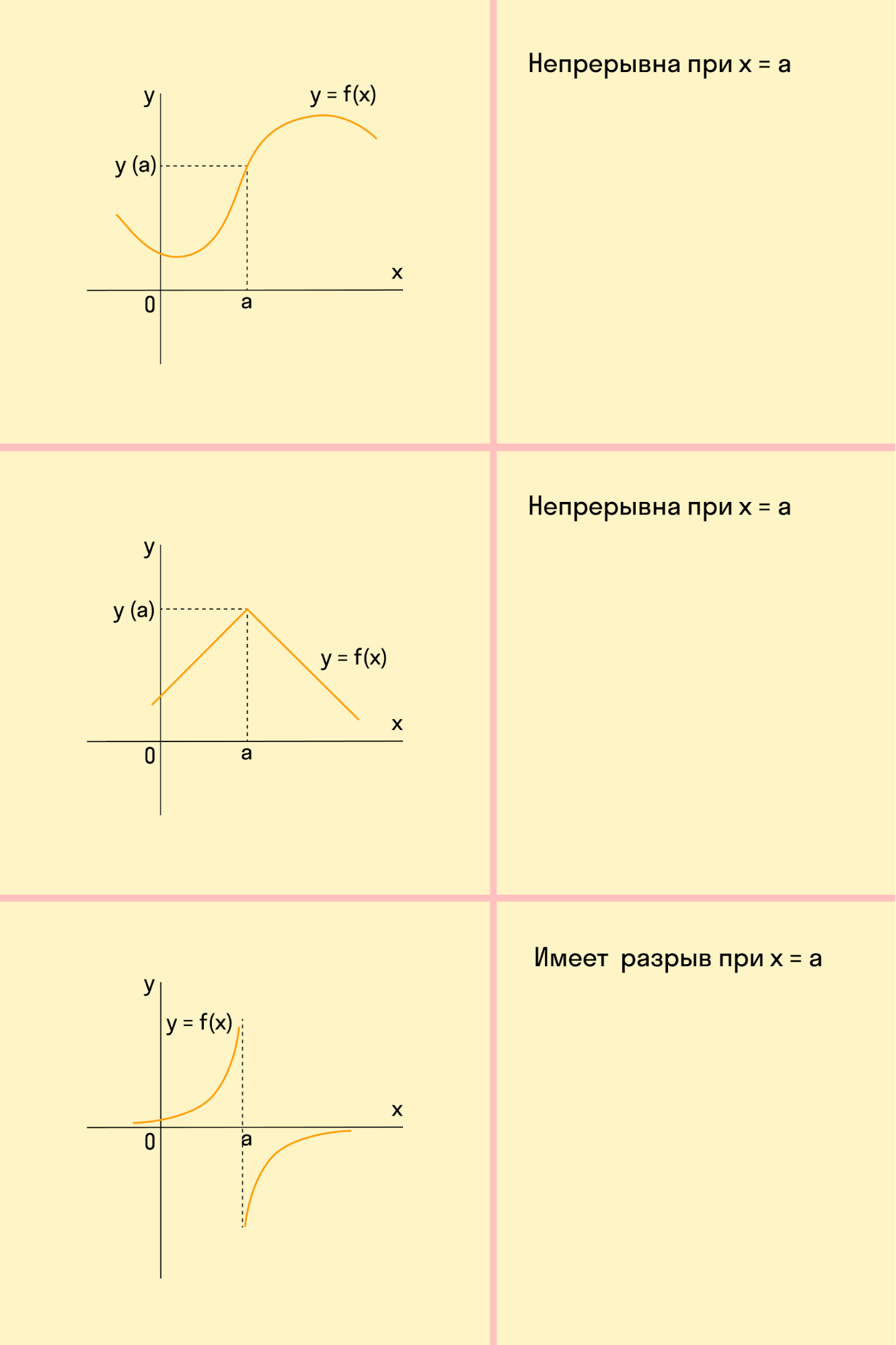
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
-
Найти область определения функции.
-
Найти область допустимых значений функции.
-
Проверить не является ли функция четной или нечетной.
-
Проверить не является ли функция периодической.
-
Найти точку пересечения с осью OY (если она есть).
-
Вычислить производную и найти критические точки, определить промежутки возрастания и убывания.
-
Промежутки знакопостоянства.
-
Асимптоты.
-
На основании проведенного исследования построить график функции.
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах или воспользуйтесь онлайн тренажером.
Задача 1. Построим график функции
Как решаем:
Упростим формулу функции:
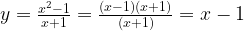
График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).
Задача 2. Построим график функции
Как решаем:
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Задача 3. Построить графики функций:
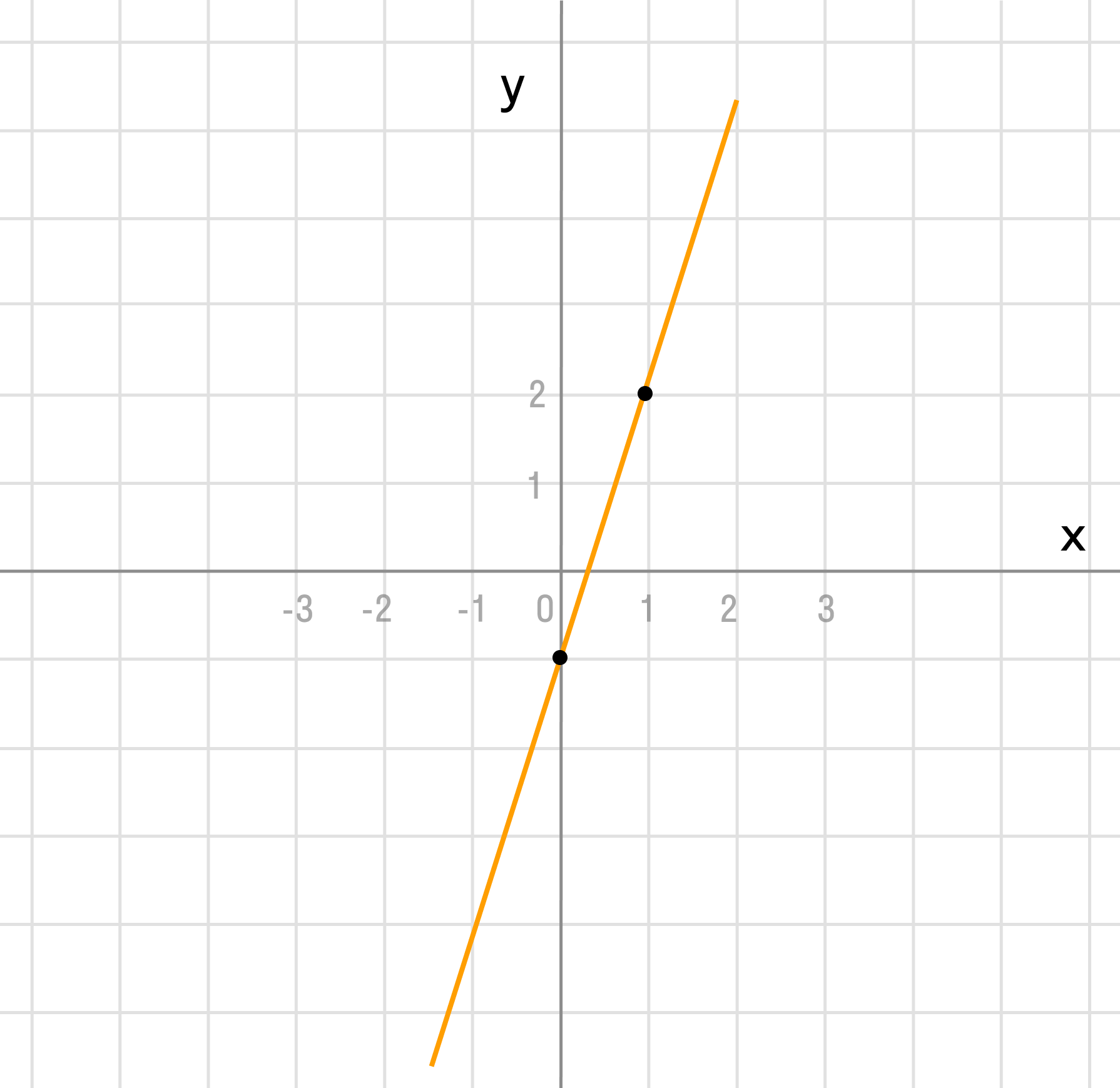
а) y = 3x — 1
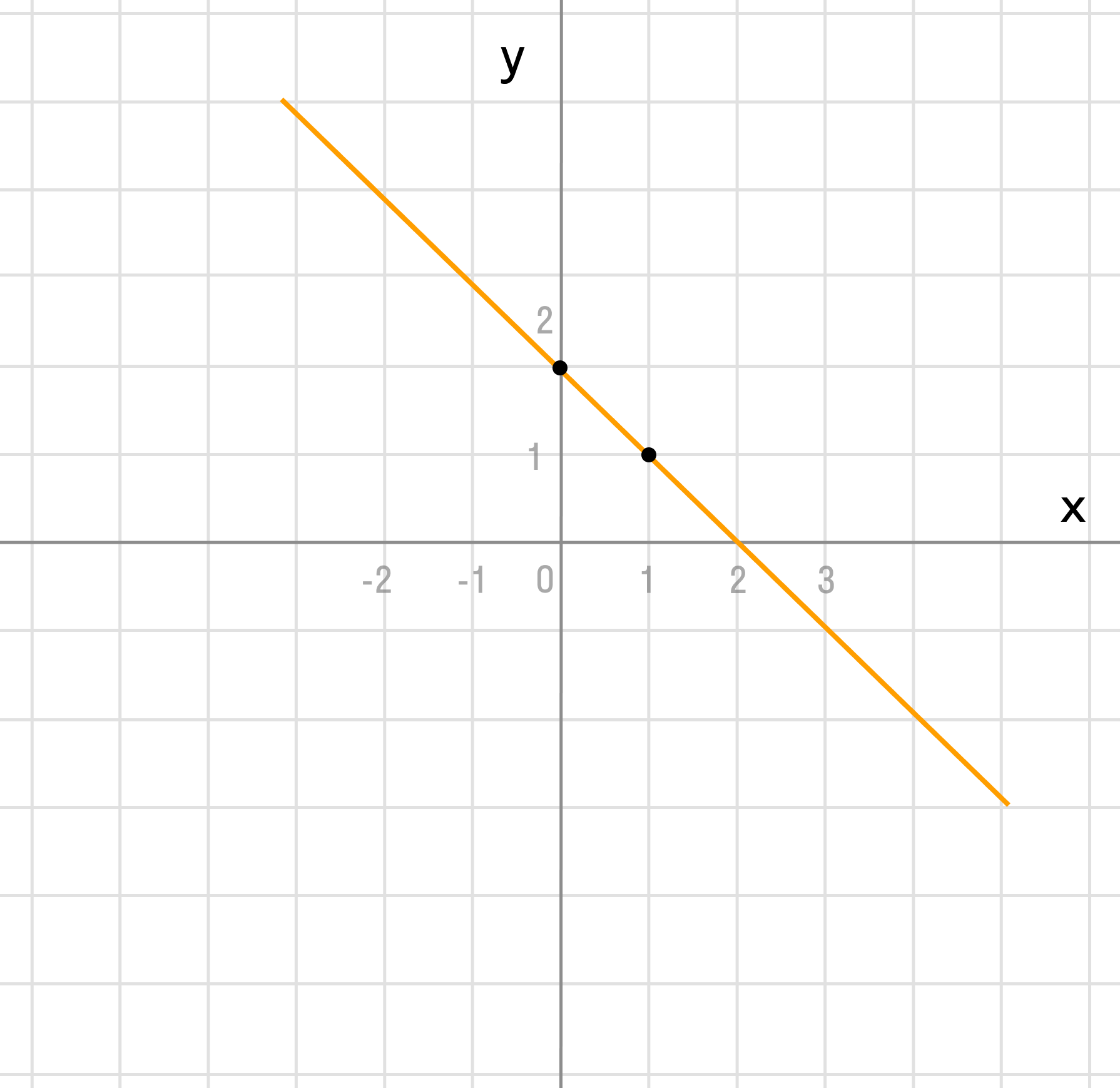
б) y = -x + 2
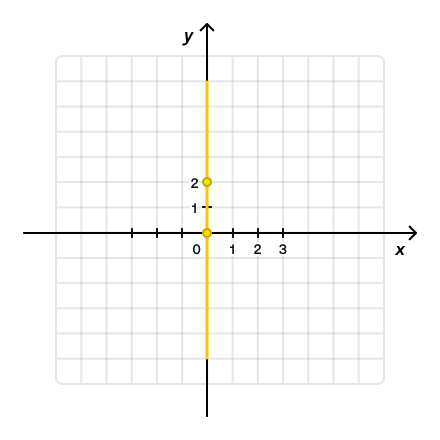
в) y = 2x
г) y = -1
Как решаем:
Воспользуемся методом построения линейных функций «по точкам».
а) y = 3x — 1
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
б) y = -x + 2
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
в) y = 2x
k = 2 > 0 — угол наклона к оси Ox острый, b = 0 — график проходит через начало координат.
г) y = -1
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
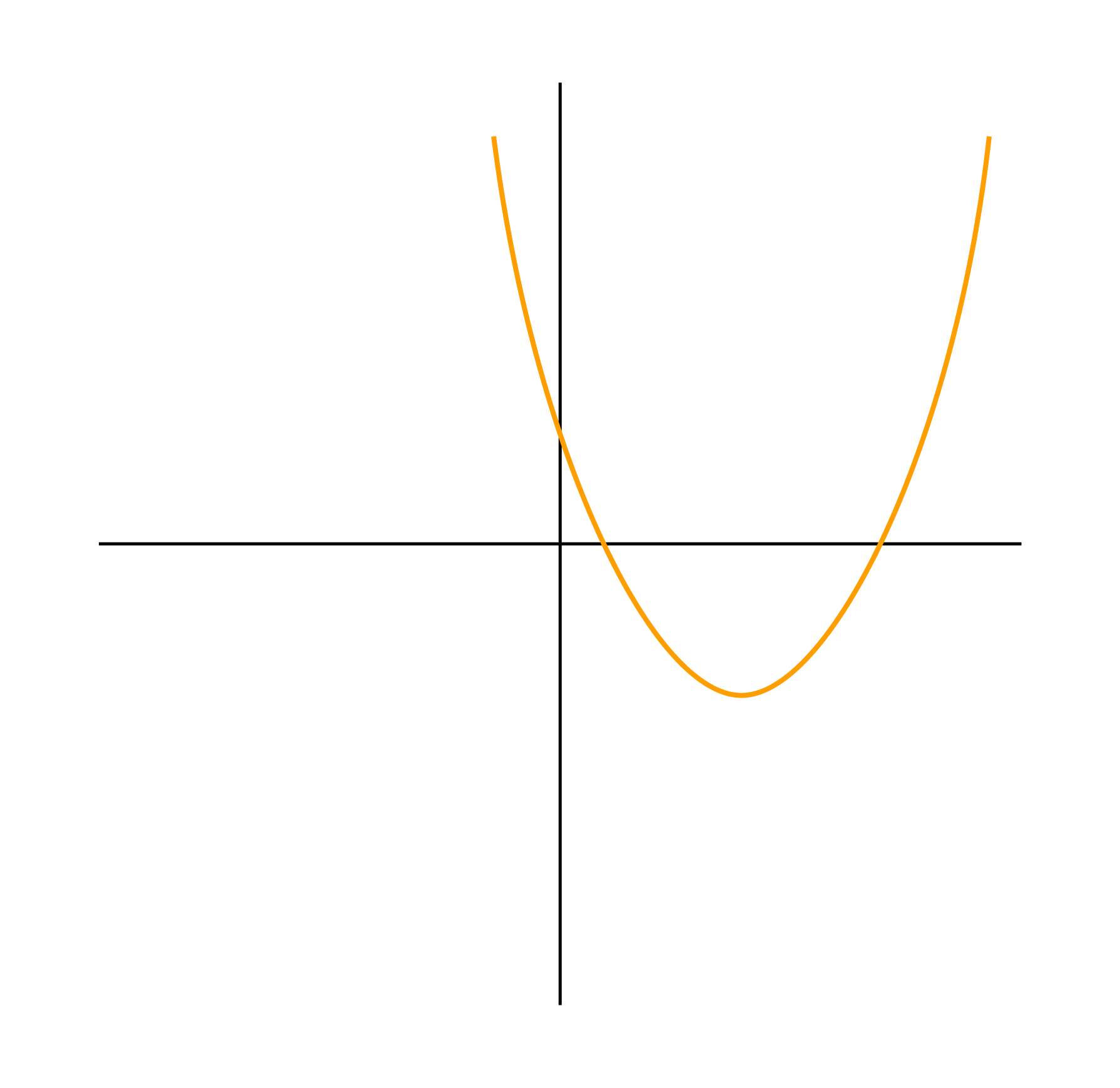
Задача 4. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Как решаем:
Вспомним, как параметры a, b и c определяют положение параболы.
-
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины
-
Ветви вверх, следовательно, a > 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
-
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
Задача 5. Построить графики функций:
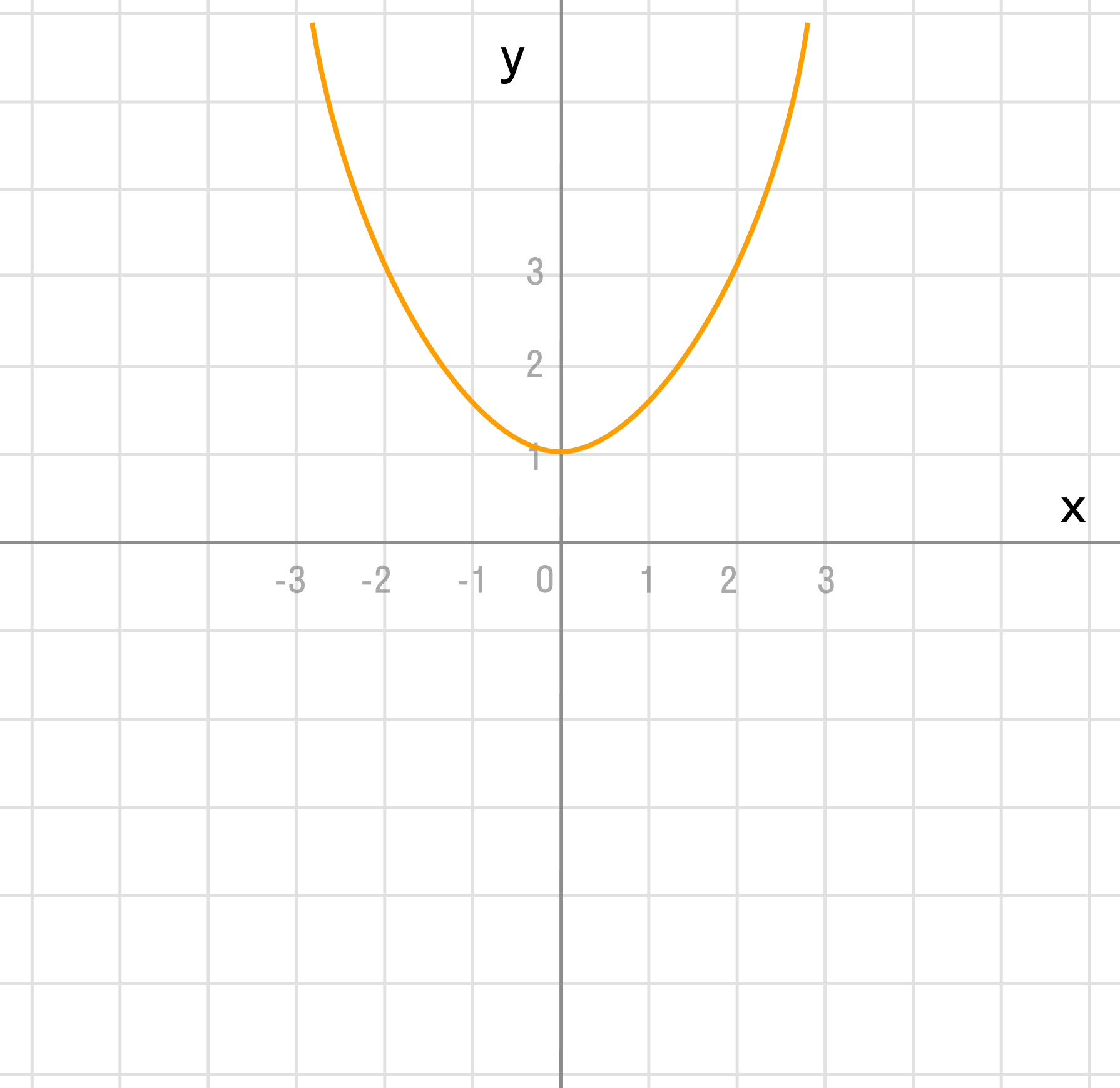
а) y = x² + 1
б)
в) y = (x — 1)² + 2
г)
д)
Как решаем:
Построить графики можно при помощи элементарных преобразований.
Если построен график функции y = f(x), то при a > 0 следующие графики получаются с помощью сдвига графика f(x).
-
y = f(x) + a — график функции y = f(x) сдвигается на a единиц вверх;
-
y = f(x) − a — график функции y = f(x) сдвигается на a единиц вниз;
-
y = f(x + a) — график функции y = f(x) сдвигается на a единиц влево;
-
y = f(x − a) — график функции у = f(x) сдвигается на a единиц вправо.
Преобразование график по типу y = mf(x): y = f(x) → y = mf(x), где m — положительное число.
-
Если m > 1, то такое преобразование графика называют растяжением вдоль оси y с коэффициентом m.
-
Если m < 1, то такое преобразование графика называют сжатием к оси x с коэффициентом 1/m.
а)
Преобразование в одно действие типа f(x) + a.
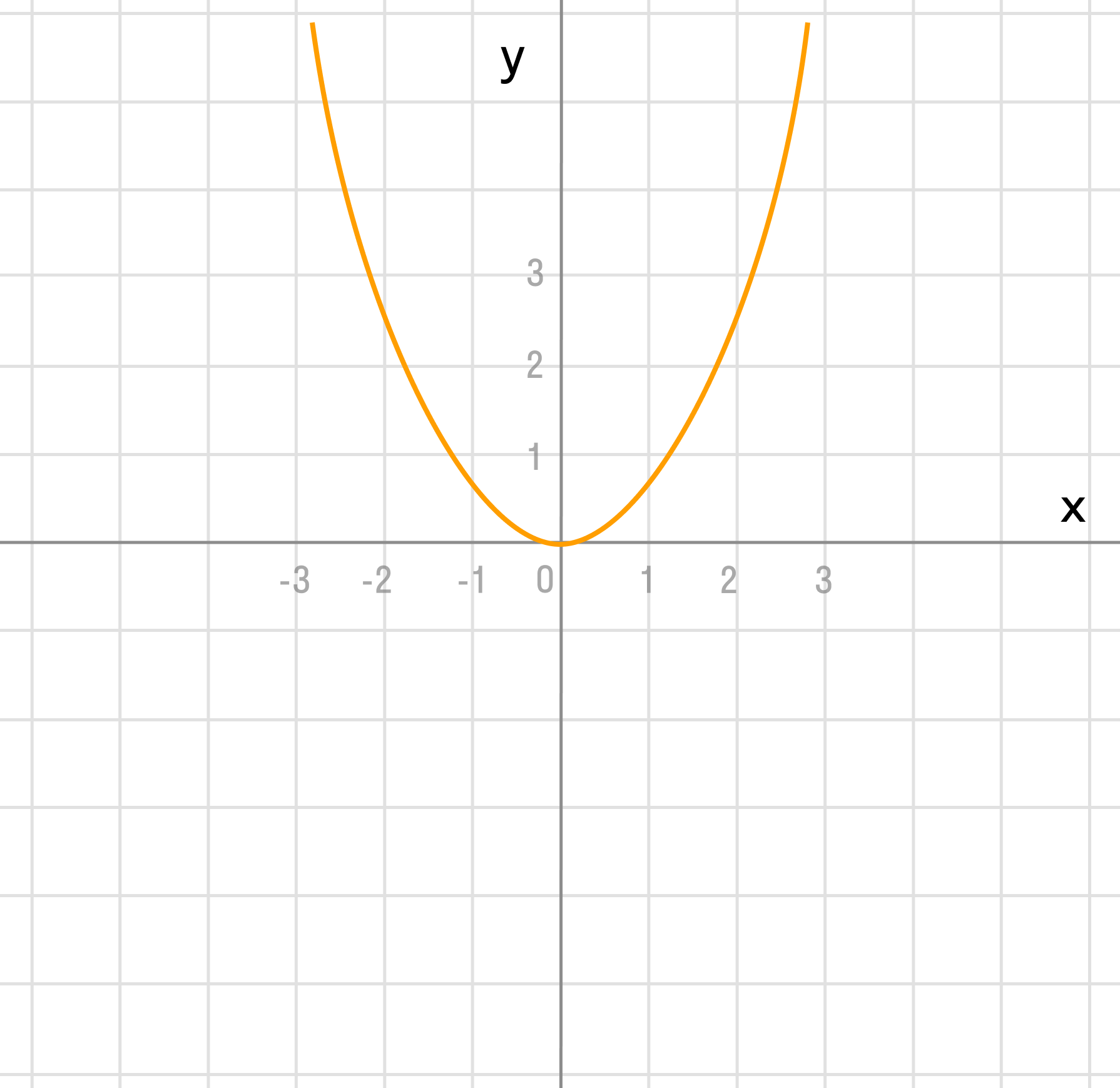
y = x²
Сдвигаем график вверх на 1:
y = x² + 1
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
в) y = (x — 1)² + 2
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
y = x²
Сдвигаем график вправо на 1:
y = (x — 1)²
Сдвигаем график вверх на 2:
y = (x — 1)² + 2
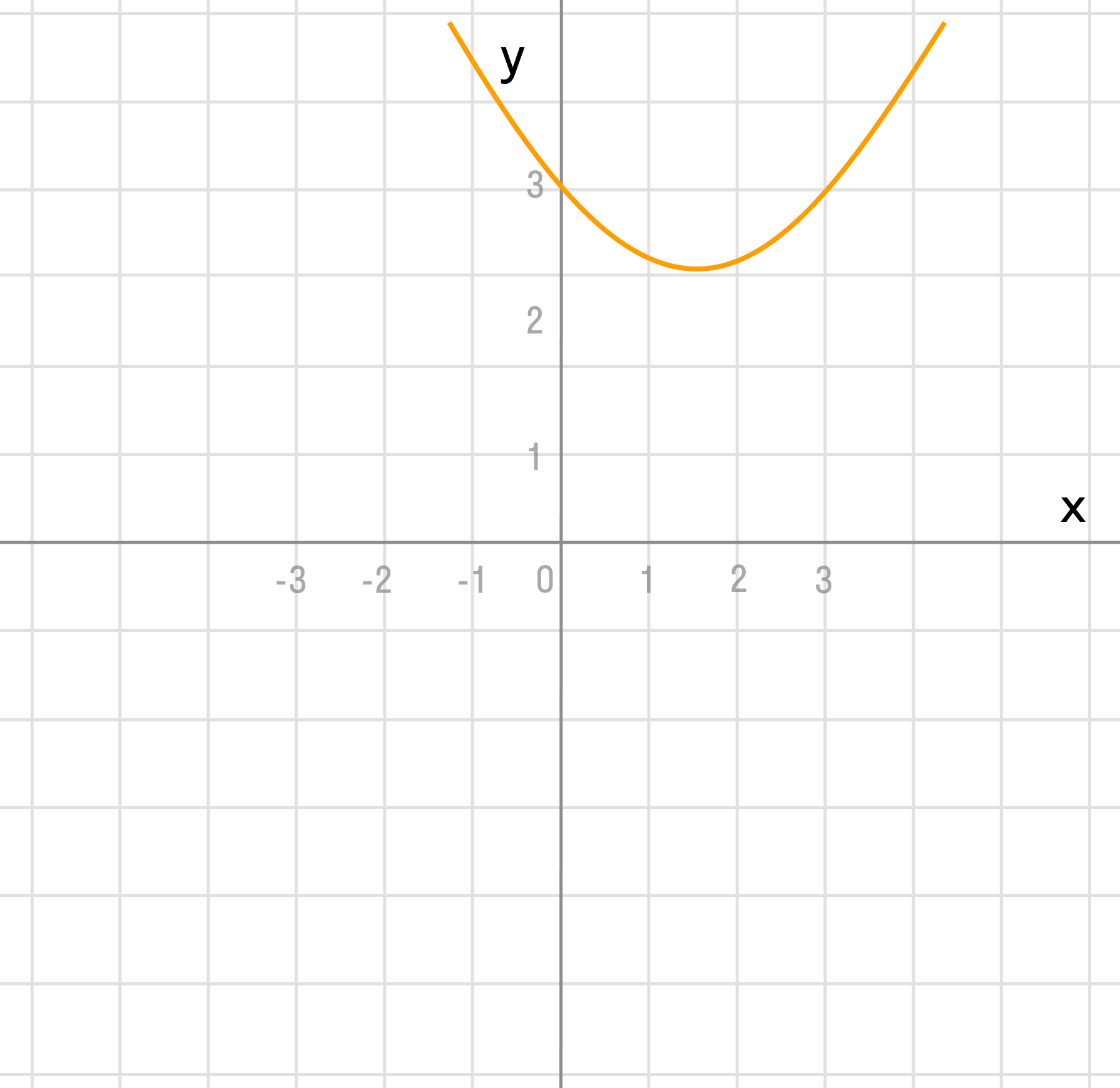
г)
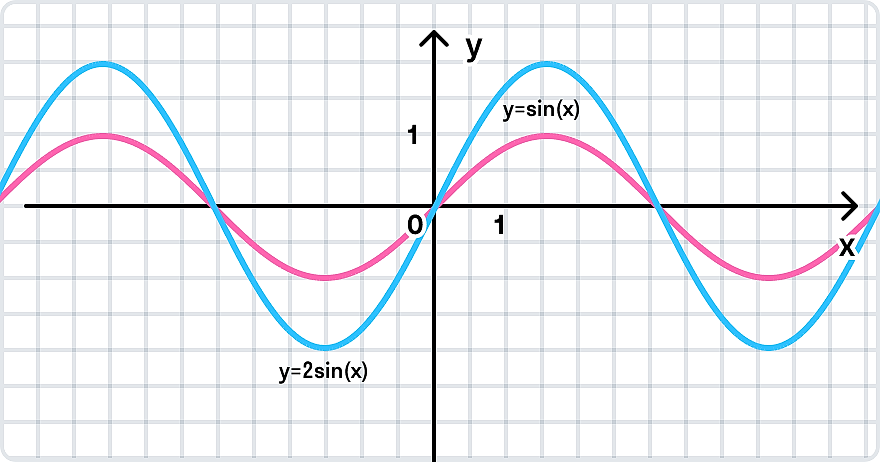
Преобразование в одно действие типа
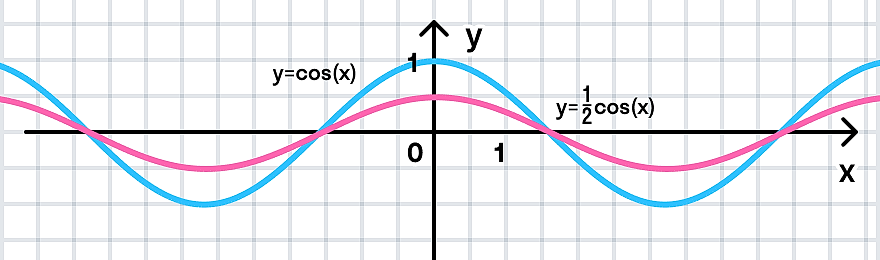
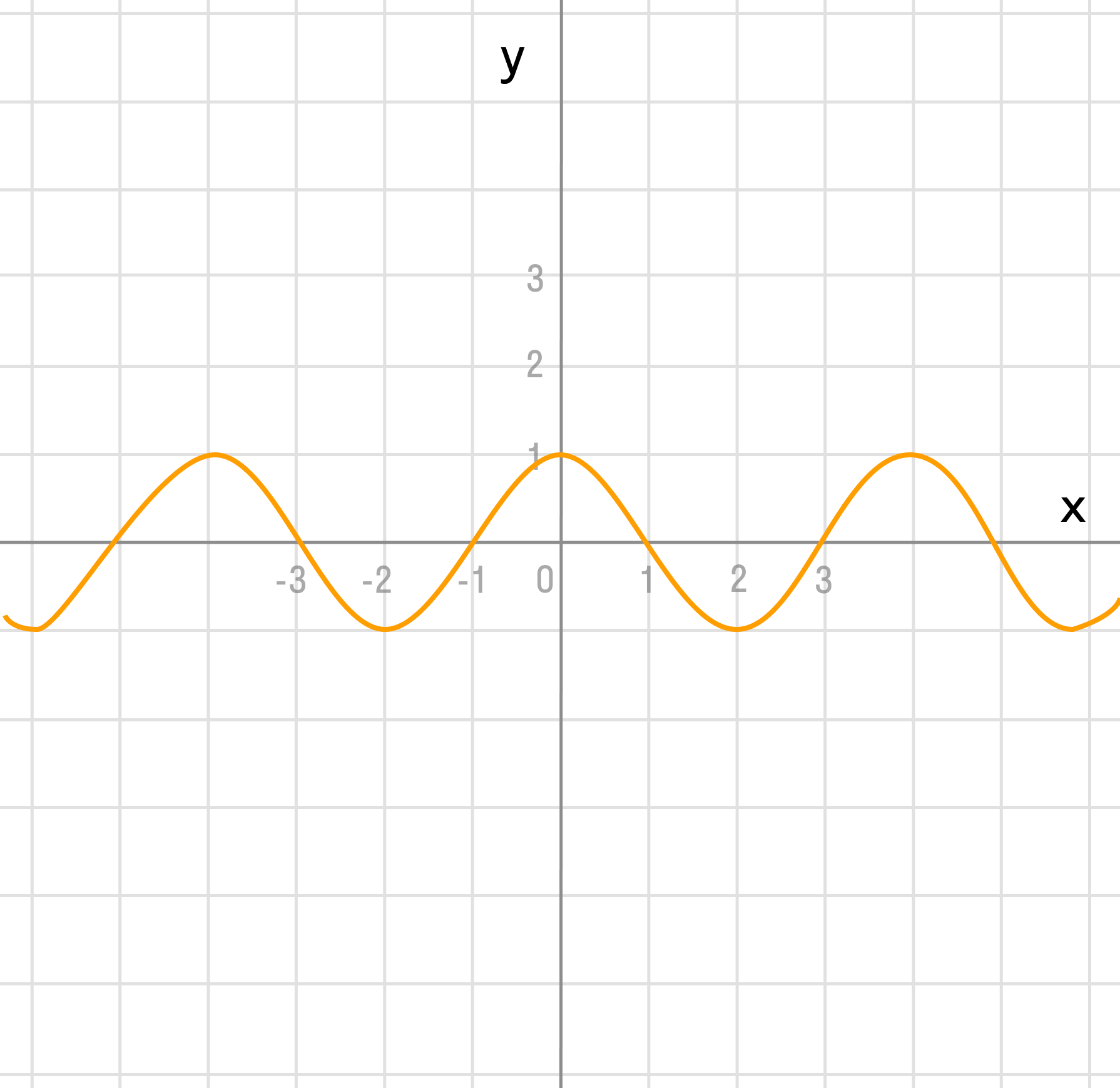
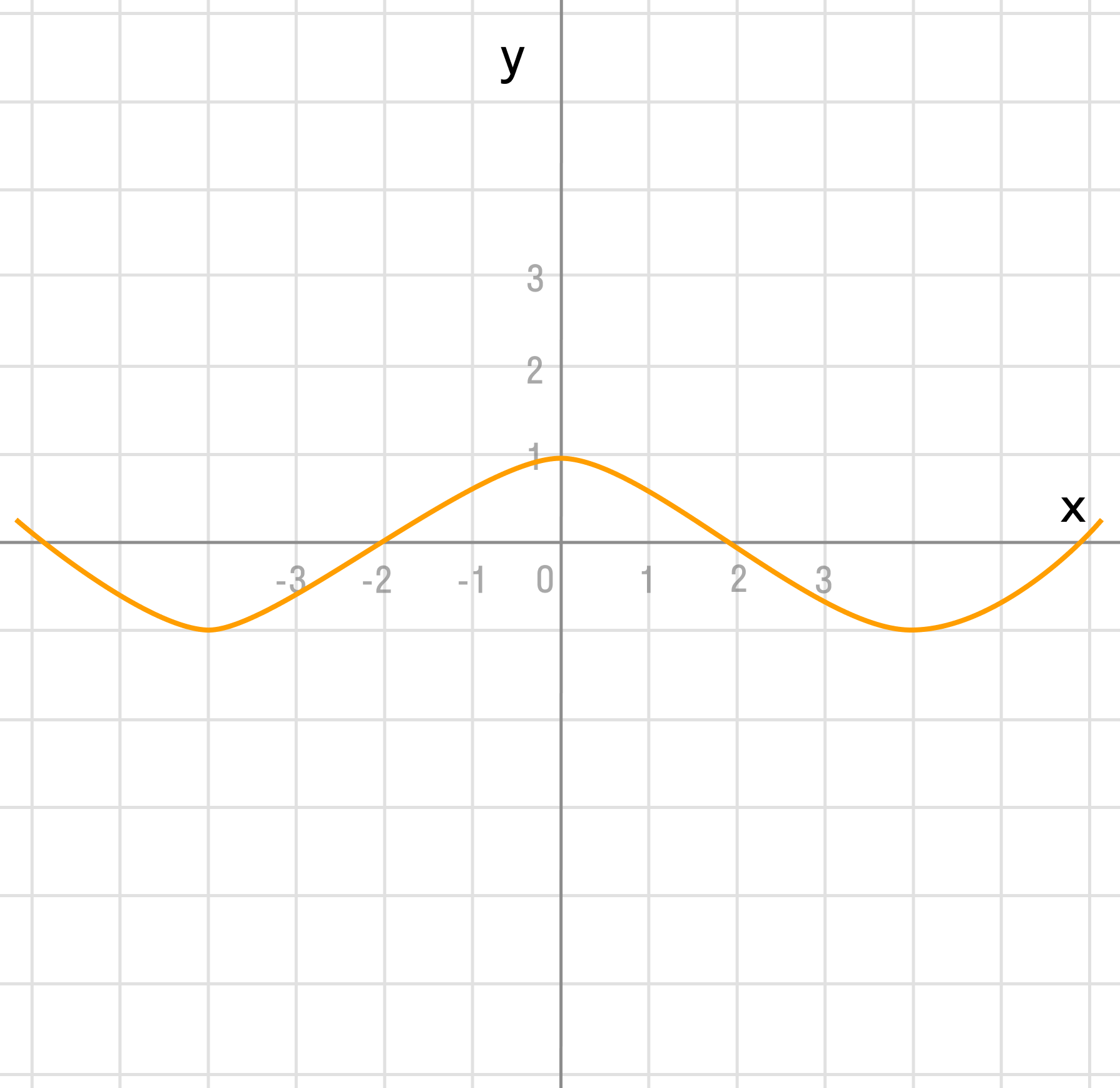
y = cos(x)
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
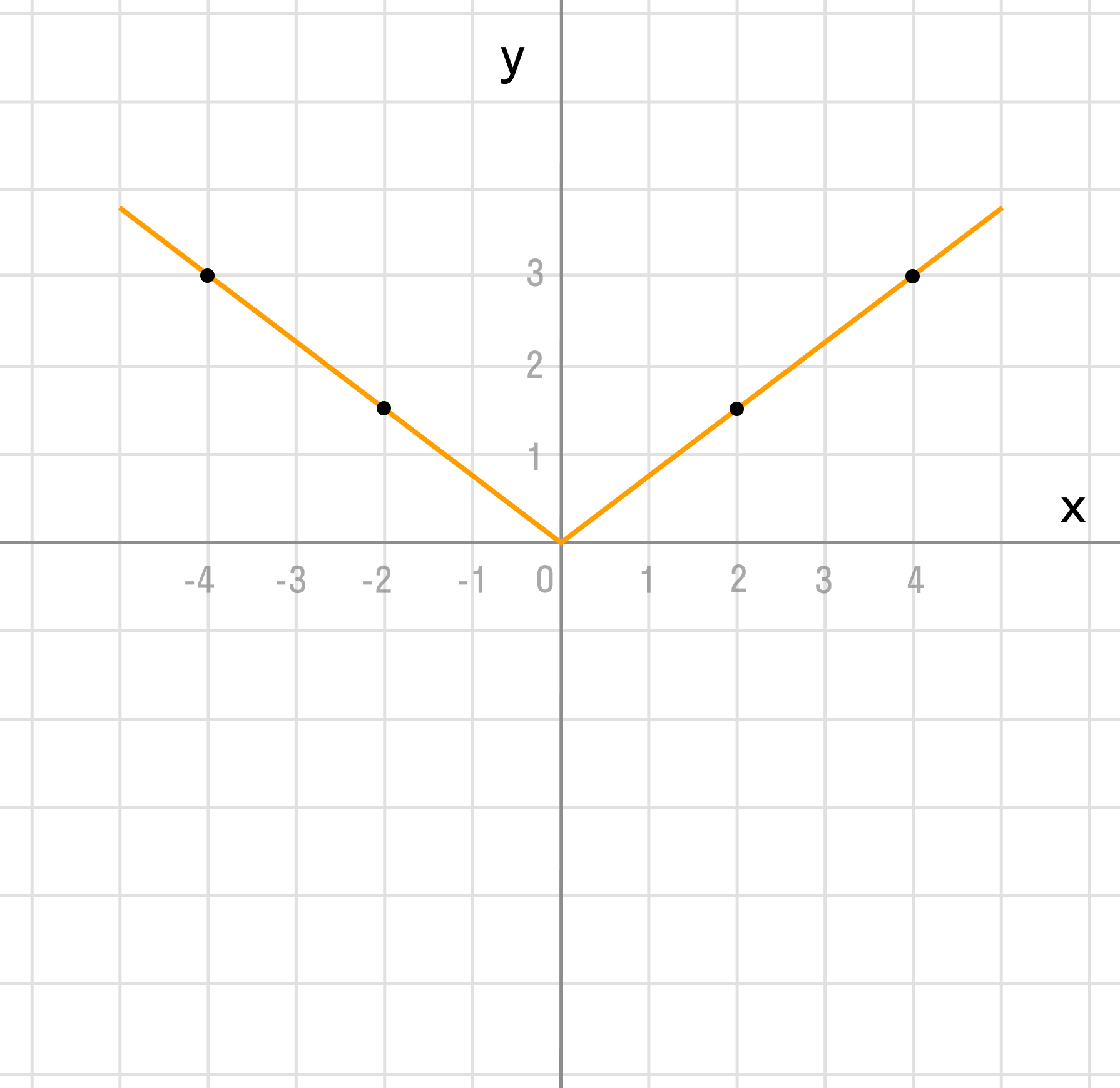
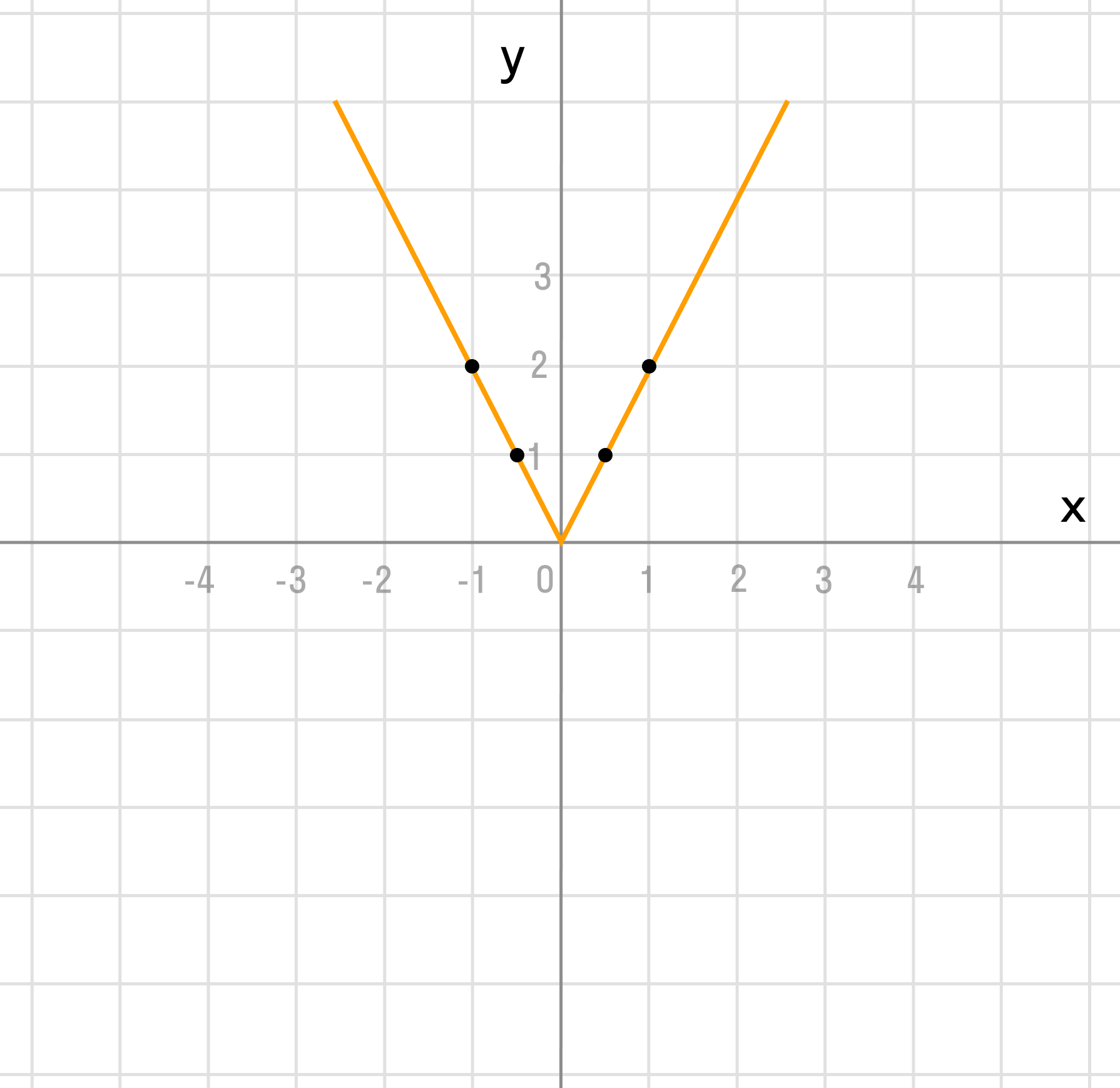
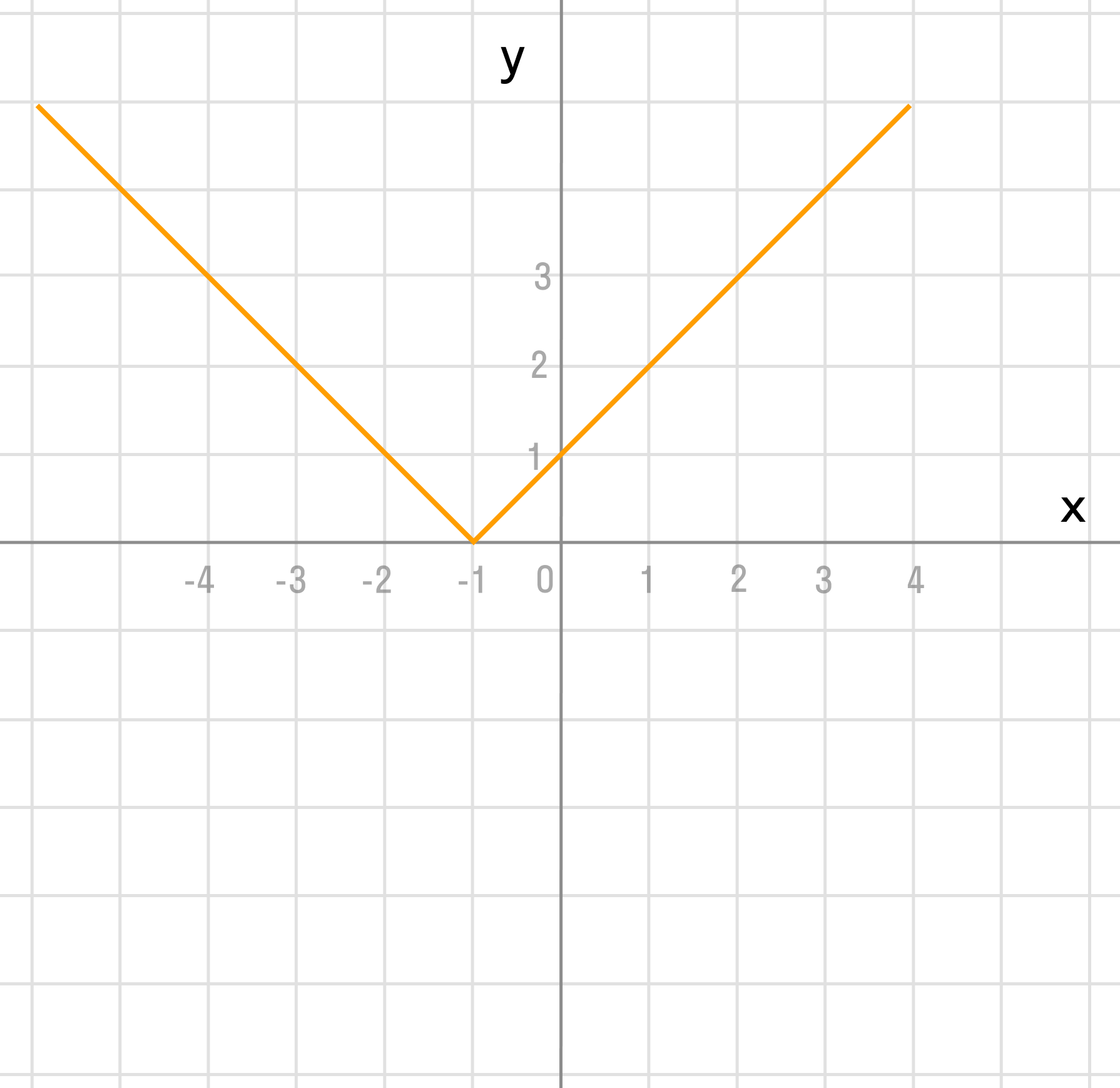
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
ПЛАН-КОНСПЕКТ УРОКА
учителя математики Салаховой М.Д.
«Функция 
Класс: 8
Тема и номер урока в теме: Функция 
Базовый учебник: Алгебра: учебник для 8 класса общеобразовательных учреждений/[Ю.Н.Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б.Суворова]; под ред. С.А.Теляковского.-М.:Просвещение,2008
Цель урока: сформулировать определение обратной пропорциональности, рассмотреть её свойства и график
Задачи:
- обучающие повторить понятие функции, их виды и графики, научить находить значение функции и аргумента по формуле у =
, строить график обратной пропорциональности, сформировать чёткое представление о различиях свойств и расположения графика функции при различных значениях k.
- развивающие продолжить развитие познавательного интереса к изучению алгебры; развивать умение анализировать, наблюдать, сопоставлять, логически мыслить; продолжить развитие элементов творческой деятельности учащихся, через вовлечение их в работу частично поискового характера, развитие навыков взаимоконтроля и самоконтроля.
- воспитательные воспитание навыков умения слушать и слышать другого, уважения к мнению товарища; воспитание у учащихся таких нравственных качеств, как настойчивость, аккуратность, инициативность, точность, привычка к систематичному труду, самостоятельность, активность; воспитание культуры общения.
Тип урока: изучение нового материала
Формы работы учащихся: фронтальная, индивидуальная, групповая
Необходимое техническое оборудование: компьютер, доска, экран, раздаточный материал
СТРУКТУРА И ХОД УРОКА
Деятельность учителя
Деятельность ученика
Время
(в мин.)
1
2
3
4
5
1
Организационный момент
Приветствие, проверка подготовленности к учебному занятию, организация внимания детей
– Девизом занятия я взяла слова:
- «Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью» Л.Н.Толстого
– Как вы понимаете это высказывание?
На доске написано высказывание.
Слушают учителя
Учащиеся выступают, как они понимают данное высказывание
1
2
Актуализация знаний учащихся
(индивидуальная, фронтальная работа)
- Какую общую тему мы изучаем?
(Сложение, вычитание, умножение и деление рац. дробей)
– Мы проверим, как вы усвоили эту тему.
– Запишите классная работа, дату на полях.
Индивидуальная, фронтальная работа:
- Несколько человек выполняют задания на карточках.
- Индивидуально один ученик за компьютером выполняет задание в электронном учебнике.
- Остальные выполняют задания, записанные на доске:
1.Выполнить действия:
а) 
2. Как называется данная функция, указать ООФ и что представляет собой их график?
y = 2x + 3, (Линейная функция, ООФ: х- л.ч., График: прямая)
y = x2, (Квадратичная функция, ООФ: х- л.ч., График: парабола)
y = x3. (Кубическая функция, ООФ: х- л.ч., График: кубическая парабола)
y = 2x, (Прямая пропорциональность, ООФ: х-л.ч., График: прямая, проходящая через начало координат)
y=8/x
– Все ли функции, приведённые в этом задании, вам знакомы?
– Сегодня мы будем изучать новую тему «Функция
Проверка выполнения заданий на компьютере.
Учащиеся сдают индивидуальные карточки.
Оценивание.
– Подведем итоги: вы повторили действия с рациональными дробями, вспомнили виды функций и их графики.
Выполняют на карточках задание 4 человека;
один ученик выполняет тесты за компьютером и вводит ответ.
Учащиеся по одному выходят к доске и записывают решение, отвечают на вопросы учителя.
Функция вида м y=8/x новая для нас, мы будем ее изучать
5
3
Постановка цели и задач урока
Объяснение нового материала
(работа в парах, фронтальная работа)
– Сегодня мы изучаем новую тему «Функция
– Какие цели и задачи поставим на занятии?
(Научиться строить график функции, узнать свойства, узнать, где используется)
Каждая функция описывает какие-то процессы, происходящие в окружающем нас мире.
1)
– Закончите предложения:
а) С увеличением цены за единицу товара количество товара, которое можно закупить на данную сумму денег … (уменьшится)
б) С уменьшением скорости движения на данном отрезке пути время движения …(увеличится)
в) С увеличением производительности труда при выполнении данного объёма работы количество рабочих … (уменьшится)
– Какую общую особенность вы заметили: как по отношению друг к другу ведут себя данные величины – количество товара и цена, скорость и время движения.
2) Рассмотрим задачу:
– Площадь прямоугольника со сторонами x и y равна S. Выразите у через S и х.
– Как найти площадь данного прямоугольника? (S=хy).
- Как называется данная зависимость? (Функция), где х – независимая переменная, а S – зависимая переменная.
Вывод: при увеличении одной переменной в несколько раз вторая переменная уменьшается во столько же раз. И, наоборот, при уменьшении одной переменной в несколько раз вторая переменная увеличивается во столько же раз.
Как можно назвать такую зависимость переменных? (обратная пропорциональность)
3)
– Самостоятельно найдите в учебнике ответ как называется функция вида 
Обратной пропорциональностью называется функция вида 
4)
–Задание – кластер: определить функции, относящиеся к обратной пропорциональности (выполнение на слайде)
5) Исследуем (работа в парах)
Построение графика функции (по рядам)
1 ряд : 

– Назовите основные этапы построения графика функции
1) Составим таблицу значений для х и у
2) Начертим координатную плоскость
3) Отметим точки в координатной плоскости
4) Соединим точки плавной линией
Учитель выясняет какие значения независимой переменной записывают в таблицу для данных функций
– Проверьте правильность заполнения таблицы.
Учитель рассматривает вопрос о зависимости расположения графика обратной пропорциональности в зависимости от знака k
Графиком обратной пропорциональности при различных значениях k (k≠0) является линия, состоящая из двух ветвей, и называемая гиперболой. Если k>0, то график функции расположен в I и III координатных четвертях, если k<0, то график функции расположен во II и IV координатных четвертях.
– Пересекает ли график функции оси координат? Обоснуйте свой ответ.
6) Сравнение графиков функций 

Вывод: при увеличении коэффициента k расстояние между ветвями гиперболы увеличивается.
7) Свойства функций (работа с учебником)
1. 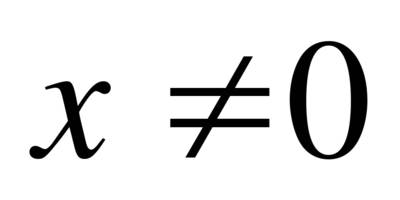
2. 

3.
Выведем свойство функции:
Даны две функции 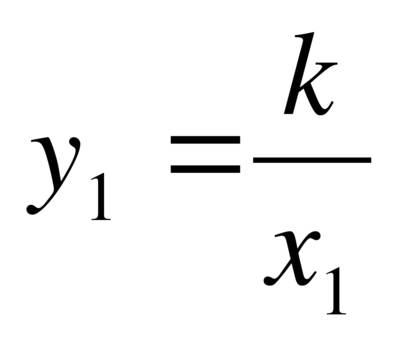




⇒ в чем смысл свойства, прочитайте (отношение двух значений аргумента равно обратному отношению соответствующих значение функции)
Учитель объясняет новый материал, выполняя необходимые записи на школьной доске: тему на доске и в тетрадях учащиеся
Учащиеся называют цели и задачи
Отвечают на вопросы учителя.
Учащиеся отвечают и записывают S=хy ⇒ y=S/x
Учащиеся самостоятельно делают вывод, учитель систематизирует
Анализируют данные в учебнике, отвечают на вопросы
Устно выполняют задание
Изучают правила построения графика функции и строят график в тетради по рядам
Один ученик у доски изменяет значение коэффициента k; учащиеся анализируют полученные результаты и делают выводы.
Отвечают на вопрос учителя:
График функции не пересекает оси координат, так как x не принимает значения x=0 (на 0 делить нельзя)
Учащиеся самостоятельно сравнивают графики функций, делают вывод
Учащиеся самостоятельно выводят и записывают свойства функции, используя учебник и данные на слайде
2+3+2+1+
+8+2+4
5
Первичное усвоение новых знаний
– Проверим первичное усвоение знаний
Выполнить задания на слайде
1)Укажите, какую из функций можно назвать обратной пропорциональностью
2) Укажите среди графиков гиперболу
3) Задайте функцию обратной пропорциональности, если ее график проходит через точку – если успеем
Выполняют задания
4
6
Первичное закрепление учебного материала
(фронтальная работа – по цепочке)
Работа с учебником №184
Выполняют задания у компьютера и в тетради.
5
7
Рефлексия (Итоги урока)
Задает вопросы ученикам:
1)Что нового вы узнали на уроке?
С какими понятиями мы сегодня познакомились?
2)Что такое обратная пропорциональность?
3)Чем отличается эта функция от всех ранее изученных?
4)Что является графиком функции 
5)В каких координатных четвертях расположен график функции?
Как называется график обратной пропорциональности?
Отвечают на вопросы учителя.
Информация о домашнем задании
Задает домашнее задание: п.8, №№ 180, 185, 195.
Записывают домашнее задание
1
Деятельность учителя
3
Приветствие, проверка подготовленности к учебному занятию, организация внимания детей
– Девизом занятия я взяла слова:
Через математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда и открытий.
А.И. Маркушевич
– Как вы понимаете это высказывание?
На доске написано высказывание.
- Какую общую тему мы изучаем?
(Сложение, вычитание, умножение и деление рац. дробей)
– Мы проверим, как вы усвоили эту тему.
– Запишите классная работа, дату на полях.
Индивидуальная, фронтальная работа:
- Несколько человек выполняют задания на карточках.
- Индивидуально один ученик за компьютером выполняет задание в электронном учебнике.
- Остальные выполняют задания, записанные на доске:
1.Выполнить действия:
а) 
2. Как называется данная функция, указать ООФ и что представляет собой их график?
y = 2x + 3, (Линейная функция, ООФ: х- л.ч., График: прямая)
y = x2, (Квадратичная функция, ООФ: х- л.ч., График: парабола)
y = x3. (Кубическая функция, ООФ: х- л.ч., График: кубическая парабола)
y = 2x, (Прямая пропорциональность, ООФ: х-л.ч., График: прямая, проходящая через начало координат)
y=8/x
– Все ли функции, приведённые в этом задании, вам знакомы?
– Сегодня мы будем изучать новую тему «Функция
Проверка выполнения заданий на компьютере.
Учащиеся сдают индивидуальные карточки.
Оценивание.
– Подведем итоги: вы повторили действия с рациональными дробями, вспомнили виды функций и их графики.
– Сегодня мы изучаем новую тему «Функция
– Какие цели и задачи поставим на занятии?
(Научиться строить график функции, узнать свойства, узнать, где используется)
Каждая функция описывает какие-то процессы, происходящие в окружающем нас мире.
1)
– Закончите предложения:
а) С увеличением цены за единицу товара количество товара, которое можно закупить на данную сумму денег … (уменьшится)
б) С уменьшением скорости движения на данном отрезке пути время движения …(увеличится)
в) С увеличением производительности труда при выполнении данного объёма работы количество рабочих … (уменьшится)
– Какую общую особенность вы заметили: как по отношению друг к другу ведут себя данные величины – количество товара и цена, скорость и время движения.
2) Рассмотрим задачу:
– Площадь прямоугольника со сторонами x и y равна S. Выразите у через S и х.
– Как найти площадь данного прямоугольника? (S=хy).
- Как называется данная зависимость? (Функция), где х – независимая переменная, а S – зависимая переменная.
Вывод: при увеличении одной переменной в несколько раз вторая переменная уменьшается во столько же раз. И, наоборот, при уменьшении одной переменной в несколько раз вторая переменная увеличивается во столько же раз.
Как можно назвать такую зависимость переменных? (обратная пропорциональность)
3)
– Самостоятельно найдите в учебнике ответ как называется функция вида 
Обратной пропорциональностью называется функция вида 
4)
–Задание – кластер: определить функции, относящиеся к обратной пропорциональности (выполнение на слайде)
5) Исследуем (работа в парах)
Построение графика функции (по рядам)
1 ряд : 

– Назовите основные этапы построения графика функции
1) Составим таблицу значений для х и у
2) Начертим координатную плоскость
3) Отметим точки в координатной плоскости
4) Соединим точки плавной линией
Учитель выясняет какие значения независимой переменной записывают в таблицу для данных функций
– Проверьте правильность заполнения таблицы.
Учитель рассматривает вопрос о зависимости расположения графика обратной пропорциональности в зависимости от знака k
Графиком обратной пропорциональности при различных значениях k (k≠0) является линия, состоящая из двух ветвей, и называемая гиперболой. Если k>0, то график функции расположен в I и III координатных четвертях, если k<0, то график функции расположен во II и IV координатных четвертях.
– Пересекает ли график функции оси координат? Обоснуйте свой ответ.
6) Сравнение графиков функций 

Вывод: при увеличении коэффициента k расстояние между ветвями гиперболы увеличивается.
7) Свойства функций (работа с учебником)
1. 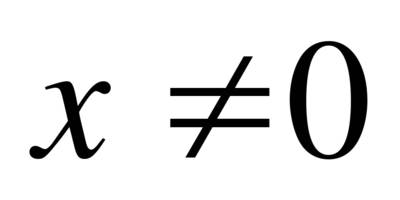
2. 

3.
Выведем свойство функции:
Даны две функции 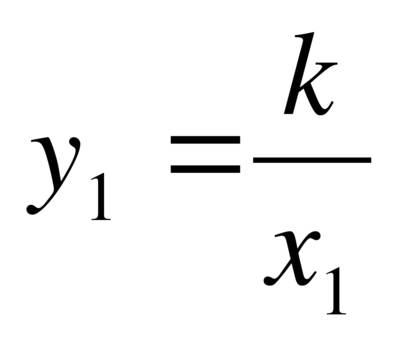




⇒ в чем смысл свойства, прочитайте (отношение двух значений аргумента равно обратному отношению соответствующих значение функции)
– Проверим первичное усвоение знаний
Выполнить задания на слайде
1)Укажите, какую из функций можно назвать обратной пропорциональностью
2) Укажите среди графиков гиперболу
3) Задайте функцию обратной пропорциональности, если ее график проходит через точку – если успеем
Работа с учебником №184
Задает вопросы ученикам:
1)Что нового вы узнали на уроке?
С какими понятиями мы сегодня познакомились?
2)Что такое обратная пропорциональность?
3)Чем отличается эта функция от всех ранее изученных?
4)Что является графиком функции 
5)В каких координатных четвертях расположен график функции?
Как называется график обратной пропорциональности?
Задает домашнее задание: п.8, №№ 180, 185, 195.






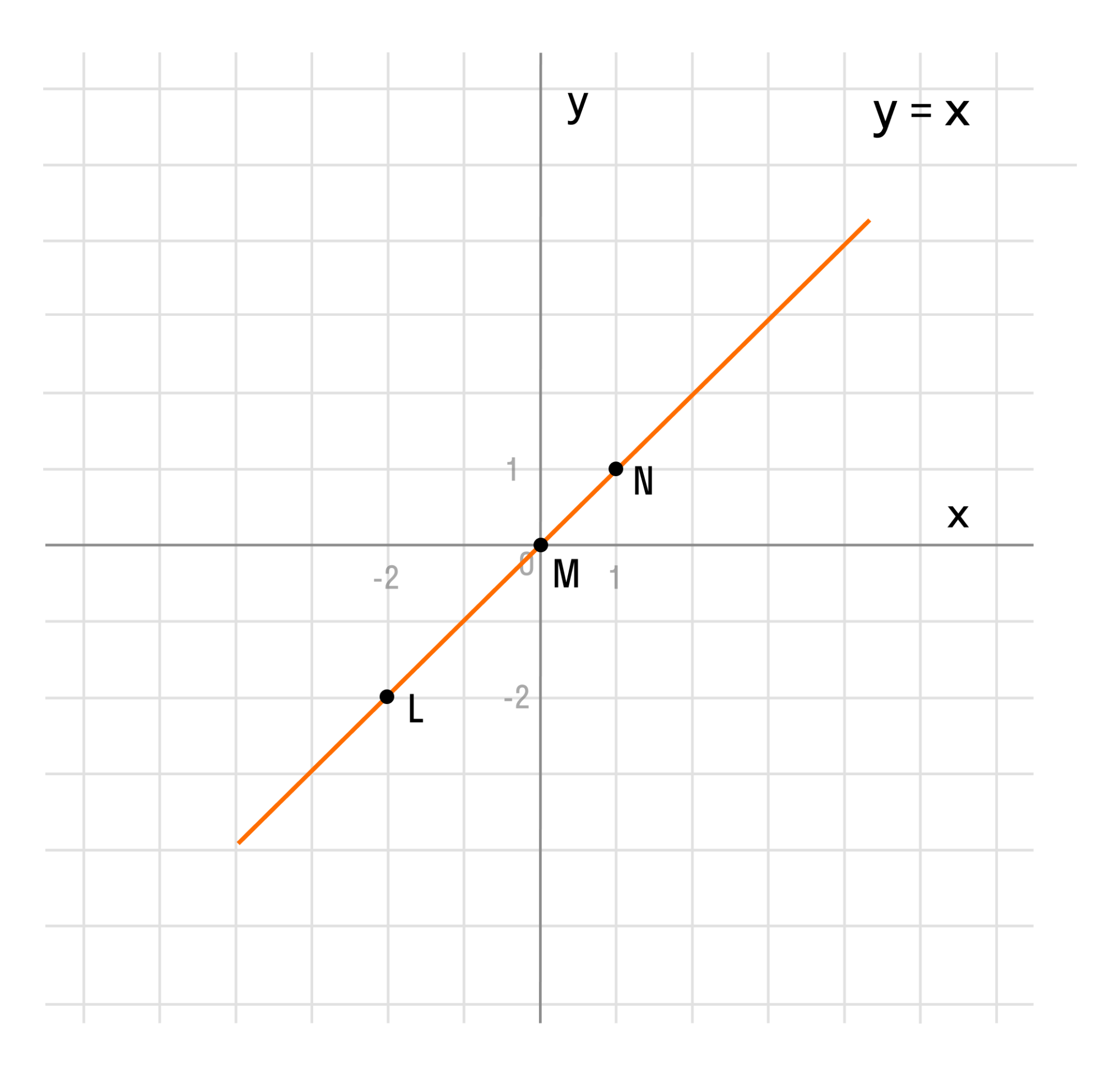
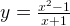
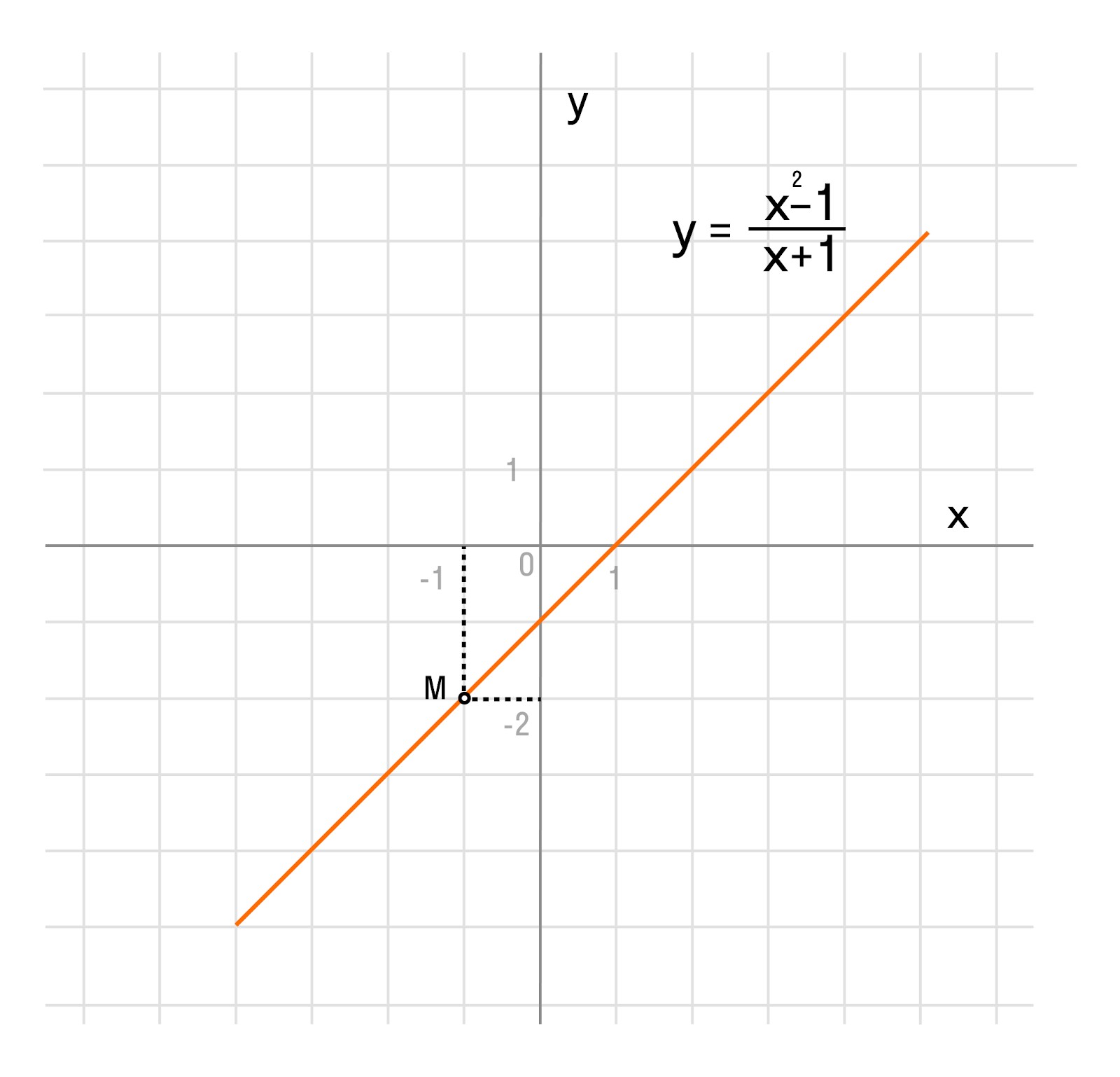
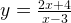
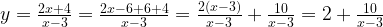
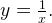
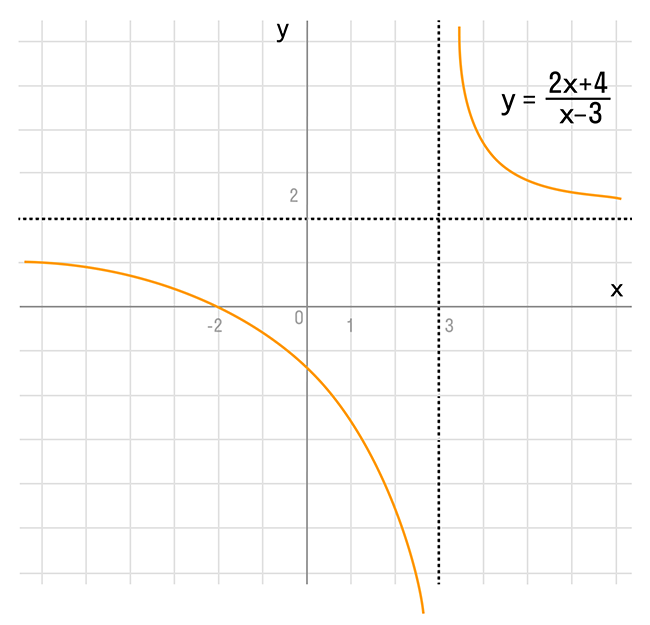
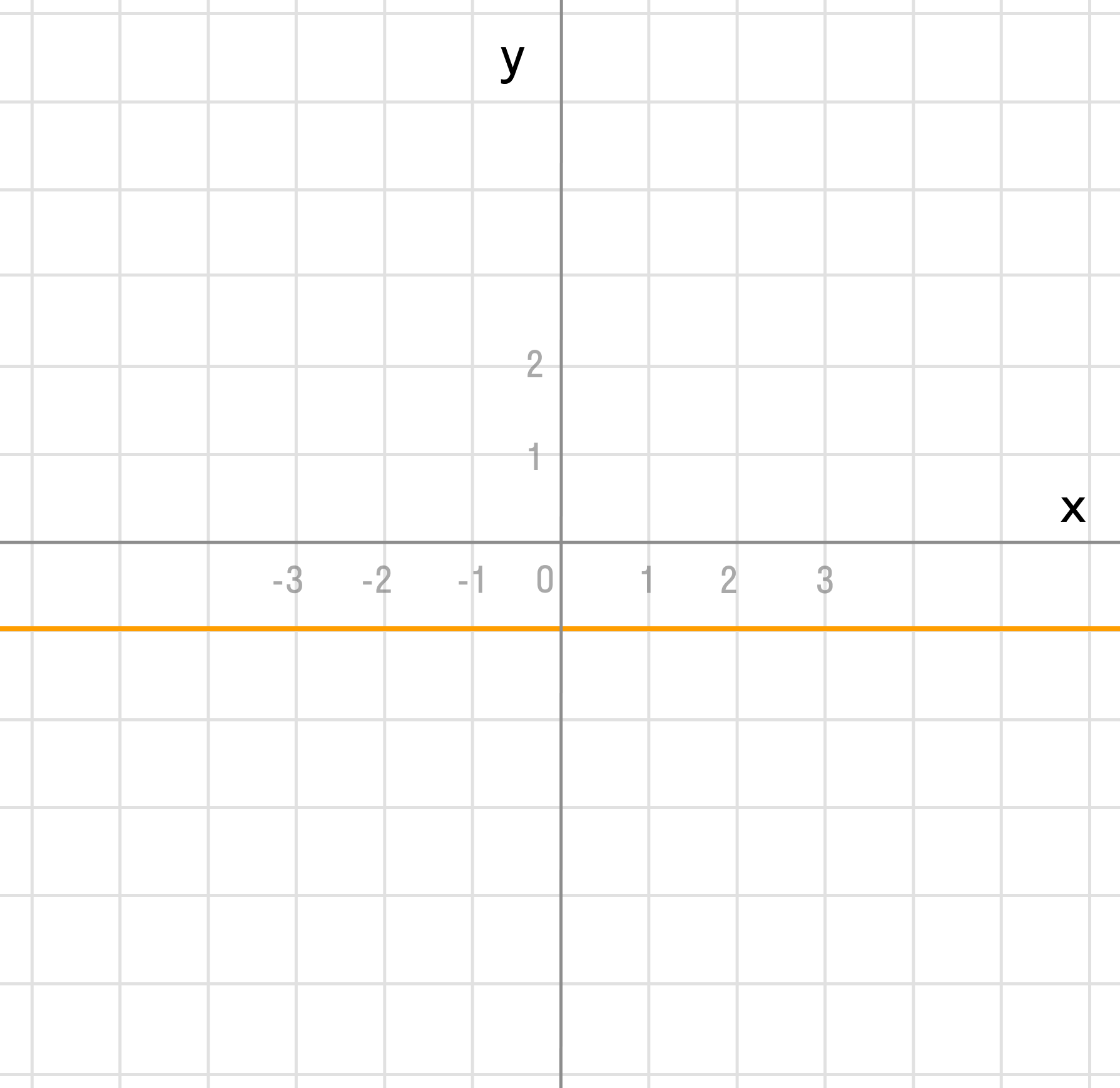
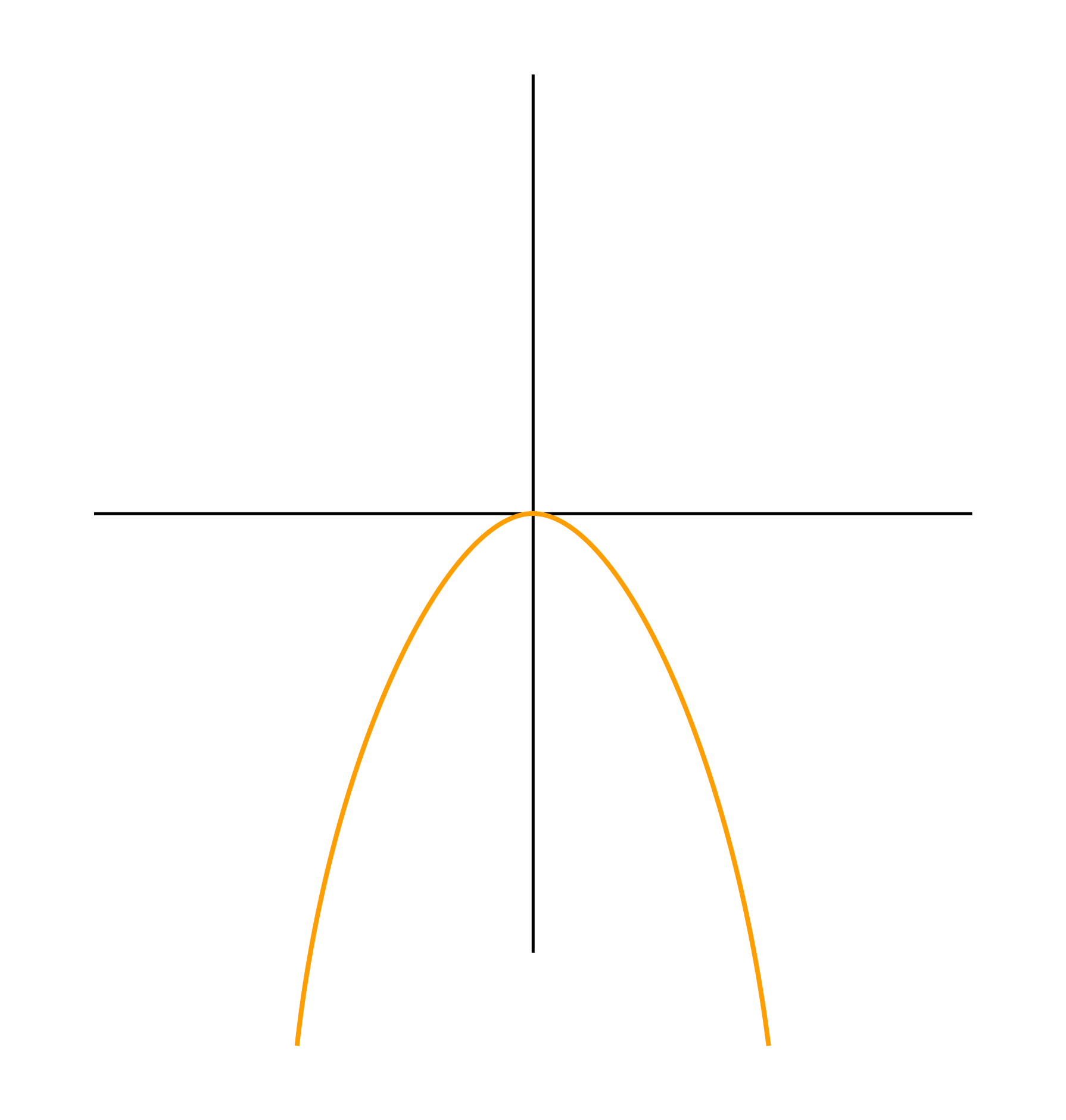
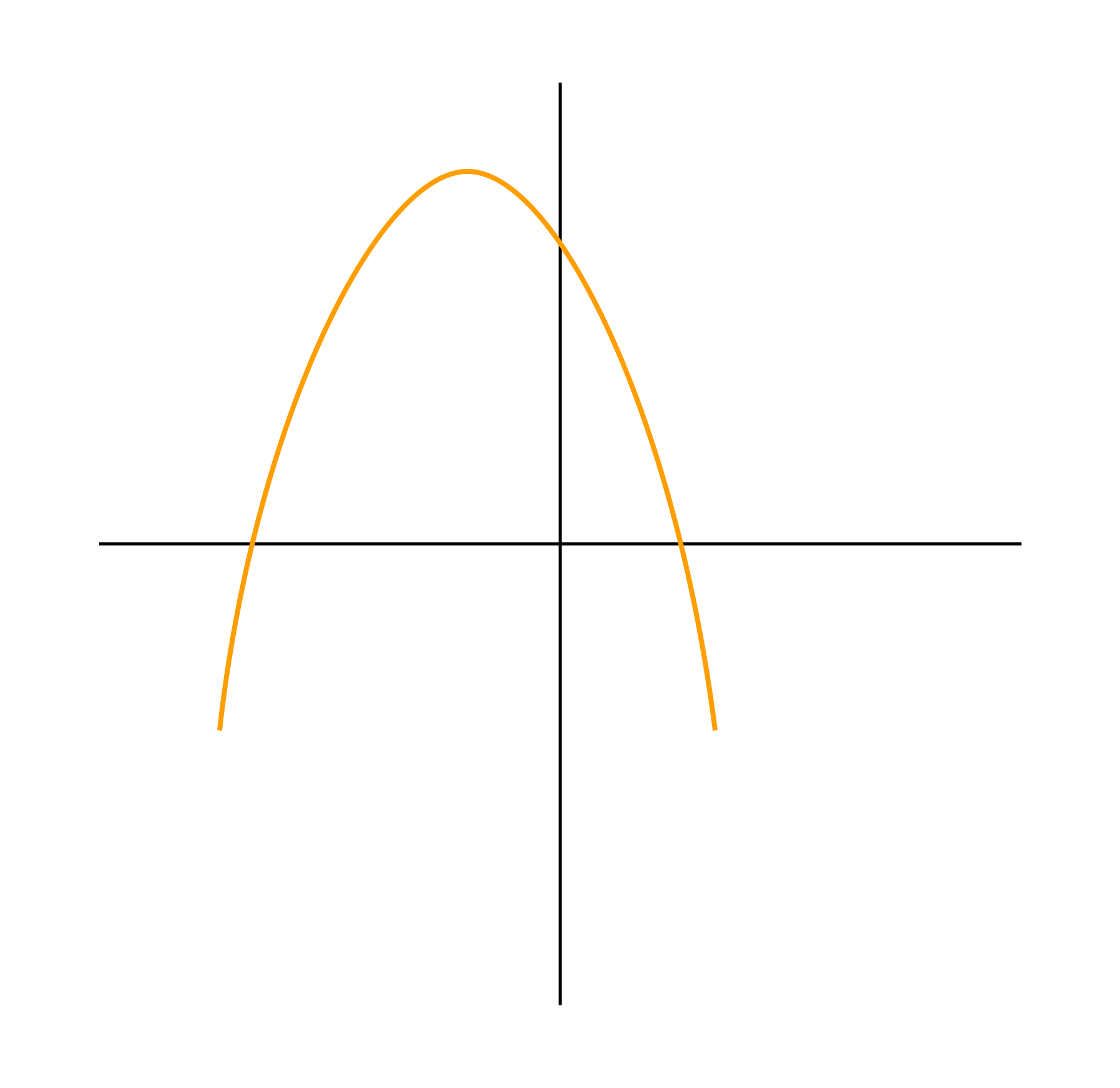
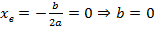
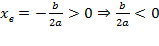 , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.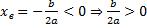 , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.