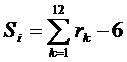Имитационное моделирование бизнес-процессов компании
Курсовая
работа на тему
«Имитационное
моделирование бизнес-процессов компании»
Самара, 2011
Введение
Имитационное моделирование — это метод исследования, при котором
изучаемая система заменяется моделью, с достаточной точностью описывающей
реальную систему и с ней проводятся эксперименты с целью получения информации
об этой системе. Экспериментирование с моделью называют имитацией (имитация —
это постижение сути явления, не прибегая к экспериментам на реальном объекте).
К имитационному моделированию прибегают, когда:
· дорого или невозможно экспериментировать на реальном объекте;
· невозможно построить аналитическую модель: в системе есть
время, причинные связи, последствие, нелинейности, стохастические (случайные)
переменные;
· необходимо сымитировать поведение системы во времени.
Цель
имитационного моделирования состоит в воспроизведении поведения исследуемой
системы на основе результатов анализа наиболее существенных взаимосвязей между
ее элементами или другими словами — разработке симулятора (англ.
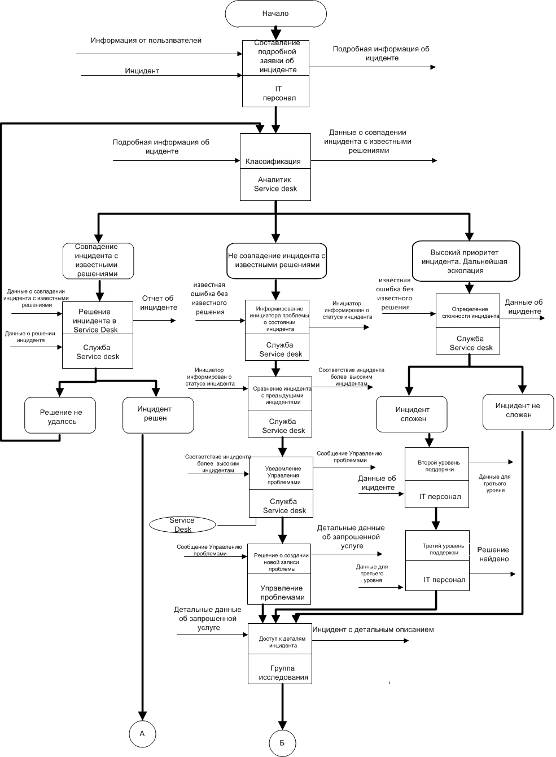
<#»560125.files/image001.gif»>
Рис. 1 — Обобщенная схема бизнес-процессов компании
3. Выбор, обоснование и детализированная схема моделируемого
бизнес-процесса
Рис. 2 — Детализированная схема бизнес-процесса — управление инцидентами
4. Определение состава исходных данных для моделирования
Таблица 1
|
Наименование параметра |
Значение |
|
Затраты от простоя |
550 |
|
Затраты от простоя ИС |
750 |
|
Затраты от простоя ПО, |
850 |
|
Затраты от простоя |
950 |
|
Затраты от простоя БД, |
600 |
|
Затраты от простоя Сервера, |
1150 |
|
Штат ИТ-службы компании |
10 |
|
Средняя заработная плата |
21 000 |
|
Количество пользовательских |
1500 |
|
Среднее количество заявок |
300 |
|
стоимость обслуживания 1 |
420 |
|
Час работы специалиста |
120 |
|
Затраты на ПО в месяц |
1000 |
|
Затраты на аппаратное |
5000 |
5. Статистическое исследование бизнес-процесса
Таблица 2 — время между инцидентами.
|
3,52 |
9,27 |
3,52 |
0,11 |
1,44 |
5,59 |
6,51 |
3,40 |
10,59 |
0,04 |
|
10,06 |
6,66 |
1,80 |
0,50 |
2,92 |
10,76 |
10,24 |
8,40 |
2,04 |
3,66 |
|
7,03 |
1,02 |
5,53 |
10,15 |
1,35 |
0,78 |
2,81 |
7,67 |
2,81 |
2,09 |
|
5,91 |
5,92 |
3,87 |
9,18 |
7,84 |
8,26 |
2,93 |
5,05 |
10,06 |
4,25 |
|
0,09 |
9,96 |
10,48 |
7,47 |
8,59 |
2,95 |
0,11 |
8,75 |
3,22 |
3,33 |
|
9,52 |
5,88 |
3,51 |
6,92 |
2,89 |
1,69 |
8,43 |
10,29 |
2,19 |
6,36 |
|
6,70 |
8,59 |
10,88 |
6,41 |
1,31 |
2,20 |
7,37 |
10,46 |
2,47 |
2,71 |
|
8,14 |
9,42 |
4,70 |
7,51 |
3,90 |
9,40 |
2,92 |
9,26 |
2,19 |
8,94 |
|
9,52 |
9,32 |
1,28 |
4,01 |
7,12 |
3,67 |
7,38 |
7,13 |
1,39 |
2,62 |
|
2,62 |
10,89 |
10,60 |
7,35 |
7,12 |
0,88 |
9,89 |
6,18 |
2,11 |
5,70 |
Таблица 3 — материальные затраты
|
178,98 |
467,83 |
248,13 |
228,54 |
501,80 |
122,63 |
264,61 |
279,30 |
133,78 |
230,70 |
|
577,69 |
681,99 |
357,86 |
83,00 |
459,22 |
58,07 |
102,30 |
574,81 |
186,60 |
594,14 |
|
229,19 |
460,82 |
649,48 |
150,68 |
440,24 |
190,09 |
150,14 |
47,12 |
110,13 |
668,13 |
|
645,89 |
290,07 |
480,06 |
531,46 |
453,05 |
354,00 |
48,07 |
584,10 |
34,68 |
605,83 |
|
238,31 |
625,40 |
542,63 |
473,13 |
389,72 |
26,19 |
137,11 |
11,82 |
103,93 |
167,42 |
|
70,72 |
567,89 |
486,92 |
77,70 |
578,89 |
26,64 |
198,67 |
668,09 |
670,87 |
545,66 |
|
116,20 |
599,10 |
210,29 |
117,46 |
617,72 |
196,71 |
216,42 |
452,75 |
553,84 |
91,92 |
|
23,40 |
230,24 |
354,62 |
315,46 |
333,96 |
341,13 |
454,22 |
433,06 |
136,05 |
613,18 |
|
307,08 |
218,06 |
206,60 |
152,26 |
489,28 |
442,76 |
88,68 |
661,68 |
224,70 |
563,15 |
|
581,52 |
383,67 |
568,66 |
405,23 |
123,95 |
560,72 |
290,64 |
158,62 |
42,04 |
552,73 |
Таблица 4 — количество инцидентов с сервером
|
2 |
0 |
1 |
4 |
1 |
2 |
1 |
4 |
3 |
2 |
|
3 |
0 |
4 |
3 |
2 |
3 |
1 |
1 |
0 |
1 |
|
3 |
1 |
0 |
4 |
3 |
2 |
1 |
5 |
2 |
1 |
|
5 |
1 |
2 |
1 |
2 |
1 |
1 |
1 |
1 |
4 |
|
1 |
2 |
0 |
2 |
0 |
0 |
0 |
1 |
2 |
1 |
|
2 |
3 |
2 |
0 |
0 |
1 |
0 |
3 |
0 |
1 |
|
1 |
2 |
1 |
3 |
1 |
0 |
2 |
0 |
0 |
4 |
|
2 |
1 |
4 |
3 |
2 |
1 |
3 |
1 |
1 |
4 |
|
0 |
2 |
1 |
1 |
1 |
3 |
2 |
3 |
3 |
3 |
|
3 |
2 |
5 |
3 |
2 |
4 |
4 |
2 |
3 |
0 |
6. Идентификация законов распределения случайных величин
6.1 Проверка гипотезы о распределении случайной величины по
показательному закону
Количество интервалов — 8
Уровень значимости — 0,05
Число степеней свободы — 6
Таблица 5 — Эмпирическое распределение время между инцидентами
|
начало интервала |
конец интервала |
частота |
частость |
середина интервала |
отклонение от среднего |
|
|
№ |
Xi |
Xi+1 |
Mi |
Wi |
Xi¯ |
Xi-Xв |
|
1 |
0,05 |
1,41 |
52 |
0,52 |
0,73 |
-1,98 |
|
2 |
1,41 |
2,78 |
26 |
0,26 |
2,10 |
-0,61 |
|
3 |
2,78 |
4,14 |
10 |
0,1 |
3,46 |
0,75 |
|
4 |
4,14 |
5,51 |
7 |
0,07 |
4,83 |
2,12 |
|
5 |
5,51 |
6,87 |
0 |
0 |
6,19 |
3,48 |
|
6 |
6,87 |
8,24 |
3 |
0,03 |
7,56 |
4,85 |
|
7 |
8,24 |
9,60 |
1 |
0,01 |
8,92 |
6,21 |
|
8 |
9,60 |
10,97 |
1 |
0,01 |
10,29 |
7,58 |
|
Итого: |
— |
— |
100 |
1 |
— |
— |
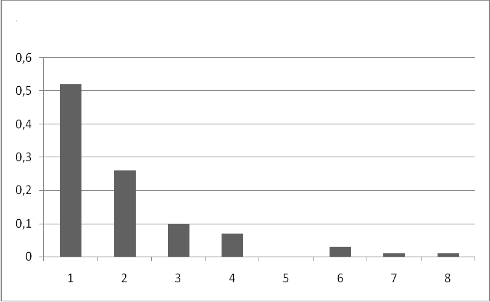
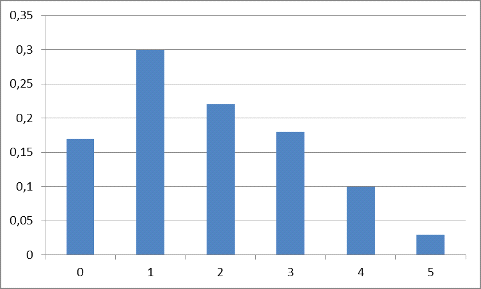
Построим гистограмму эмпирического распределения время между инцидентами
(рис. 3):
Рис. 3
Вычисление теоретических вероятностейпопадания в заданный интервал
экспоненциально распределенной случайной величины (таблица 5):
Таблица 5
|
вероятность |
теоретические частоты |
||||||
|
-л*Xi |
-л*Xi+1 |
e^(-л*Xi) |
e^(-л*Xi+1) |
Pi |
Mi’ |
(Mi-Mi’)² |
(Mi-Mi’)²/Mi’ |
|
-0,025 |
-0,697 |
0,976 |
0,498 |
0,478 |
47,784 |
17,777 |
0,372 |
|
-0,697 |
-1,370 |
0,498 |
0,254 |
0,244 |
24,384 |
2,611 |
0,107 |
|
-1,370 |
-2,043 |
0,254 |
0,130 |
0,124 |
12,443 |
5,970 |
0,480 |
|
-2,043 |
-2,716 |
0,130 |
0,066 |
0,063 |
6,350 |
0,423 |
0,067 |
|
-2,716 |
-3,388 |
0,066 |
0,034 |
0,032 |
3,240 |
10,500 |
3,240 |
|
-3,388 |
-4,061 |
0,034 |
0,017 |
0,017 |
1,654 |
1,813 |
1,096 |
|
-4,061 |
-4,734 |
0,017 |
0,009 |
0,008 |
0,844 |
0,024 |
0,029 |
|
-4,734 |
-5,407 |
0,009 |
0,004 |
0,004 |
0,431 |
0,324 |
0,753 |
|
— |
— |
— |
— |
1 |
— |
— |
6,14 |
Примем в качестве оценки параметра α показательного распределения
величину, обратную средней выборочной:
.
λ = 0,49
Выборочная
средняя = 2,03
Среднее
квадратическое отклонение σ = 2,04
Сравним
и
.
Вывод:
так как <
, то по
данным наблюдений генеральная совокупность имеет экспоненциальный закон
распределения.
6.2 Проверка гипотезы о распределении случайной величины по нормальному
закону
Количество интервалов — 8
Количество параметров распределения — 2
Уровень значимости — 0,05
Число степеней свободы — 5
Таблица 6 — Эмпирическое распределение материальные затраты
|
начало интервала |
конец интервала |
эмпирические частоты |
частость |
середина интервала |
отклонение от среднего |
|
|
№ |
Xi |
Xi+1 |
Mi |
Wi |
Xi¯ |
Xi-Xв |
|
1 |
6,52 |
91,27 |
7 |
0,07 |
48,90 |
342,29 |
|
2 |
91,27 |
176,02 |
9 |
0,09 |
133,65 |
1202,84 |
|
3 |
176,02 |
260,78 |
16 |
0,16 |
218,40 |
3494,40 |
|
4 |
260,78 |
345,53 |
19 |
0,19 |
303,15 |
5759,86 |
|
5 |
345,53 |
430,28 |
21 |
0,21 |
387,90 |
8145,92 |
|
6 |
430,28 |
515,03 |
13 |
0,13 |
472,65 |
6144,47 |
|
7 |
515,03 |
599,78 |
12 |
0,12 |
557,40 |
6688,83 |
|
8 |
599,78 |
684,53 |
3 |
0,03 |
642,15 |
1926,46 |
|
Итого: |
— |
— |
100 |
1 |
— |
— |
Продолжение Таблицы 6 — Проверка статистической гипотезы о нормальном
распределении СВ
|
Zi |
Zi+1 |
функция Лапласа |
вероятности |
теоретические частоты |
(Mi-Mi’)²/Mi’ |
|
|
Ф(Zi) |
Ф(Zi+1) |
Pi |
Mi’=n*Pi |
|||
|
-2,07576 |
-1,54351 |
0,0189581 |
0,061353026 |
0,042 |
4,239497 |
7,6203744 |
|
-1,54351 |
-1,01127 |
0,061353 |
0,155944098 |
0,095 |
9,459107 |
0,2107795 |
|
-1,01127 |
-0,47902 |
0,1559441 |
0,315961608 |
0,160 |
16,00175 |
3,066E-06 |
|
-0,47902 |
0,053225 |
0,3159616 |
0,521223534 |
0,205 |
20,52619 |
2,3292639 |
|
0,053225 |
0,585471 |
0,5212235 |
0,720884444 |
0,200 |
19,96609 |
1,0689677 |
|
0,585471 |
1,117717 |
0,7208844 |
0,868156107 |
0,147 |
14,72717 |
2,9831033 |
|
1,117717 |
1,649964 |
0,8681561 |
0,950524801 |
0,082 |
8,236869 |
14,161152 |
|
1,649964 |
2,18221 |
0,9505248 |
0,985452974 |
0,035 |
3,492817 |
0,2428689 |
|
— |
— |
— |
— |
1 |
— |
3,98 |
Выборочная
средняя = 337,05
Среднее
квадратическое отклонение σ = 159,23
Сравним
и
.
Вывод:
так как <
, то по
данным наблюдений генеральная совокупность имеет нормальный закон
распределения.
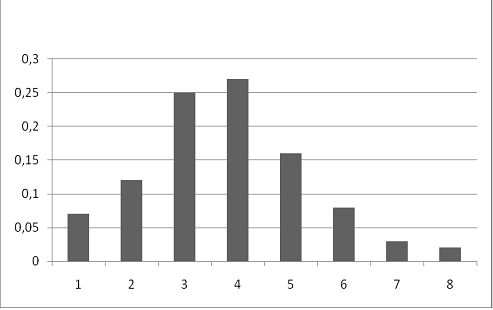
Построим
гистограмму эмпирического распределения материальные затраты (рис. 4):
Рис.
4
6.3 Проверка гипотезы о распределении случайной величины по закону
Пуассона
Количество параметров распределения — 1
Уровень значимости — 0,05
Число степеней свободы — 4
Таблица 7 — Эмпирическое распределение количества потерянных клиентов
|
№ |
Интервал |
Частота |
Частность |
Центр интервала |
Среднее выборочное |
Отклонение от среднего |
Квадрат отклонения |
|
|
1 |
0—0 |
17 |
0,17 |
0 |
0 |
-1,83 |
3,35 |
0,57 |
|
2 |
1—1 |
30 |
0,3 |
1 |
30 |
-0,83 |
0,69 |
0,21 |
|
3 |
2—2 |
22 |
0,22 |
2 |
44 |
0,17 |
0,03 |
0,01 |
|
4 |
3—3 |
18 |
0,18 |
3 |
54 |
1,17 |
1,37 |
0,25 |
|
5 |
4—4 |
10 |
0,1 |
4 |
40 |
2,17 |
4,71 |
0,47 |
|
6 |
5—5 |
3 |
0,03 |
5 |
15 |
3,17 |
10,05 |
0,30 |
|
Итого |
100 |
183 |
1,8011 |
Среднеквадратическое отклонение — 1,34
Выборочное среднее — 1,83
Дисперсия — 1,8
Построим полигон эмпирического распределения количества потерянных
клиентов (рис. 5):
Рис. 5
Вычисление вероятностей попадания в заданный интервал случайной величины,
распределенной по закону Пуассона:
Таблица 8
|
№ |
Частота |
Pi |
Мi’=N*Pi |
Мi-Мi’ |
(Мi-М’i)^2 |
(Мi-М’i)^2/Мi’ |
|
1 |
17 |
0,1604136 |
16,04136 |
0,958643 |
0,918997 |
0,057289 |
|
2 |
30 |
0,2935568 |
29,35568 |
0,644317 |
0,415145 |
0,014142 |
|
3 |
22 |
0,2686045 |
26,86045 |
-4,86045 |
23,62397 |
0,879508 |
|
4 |
18 |
0,1638487 |
16,38487 |
1,615126 |
2,608631 |
0,15921 |
|
5 |
10 |
0,0749608 |
7,49608 |
2,50392 |
6,269615 |
0,836386 |
|
6 |
3 |
0,0274357 |
2,743565 |
0,256435 |
0,065759 |
0,023968 |
|
100,00 |
0,98 |
хи-кв. набл. |
1,970503 |
кр
Гипотеза принимается, поскольку 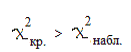
6.4 Проверка гипотезы о распределении случайной величины по закону
Бернулли
Таблица 9 — Статистические данные для случайной величины проведение дополнительной
диагностики (распределение Бернулли)
|
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
0 |
P[1] =
26/100 = 0,26
P[0] =
(100-26)/100 = 0,74
Вероятность того, что дополнительная диагностика будет проведена, равна
0,26, не будет — 0,74.
6.5 Результаты идентификации законов распределения случайных
величин
Таблица 10
|
№ |
СВ |
Закон распределения |
Параметр распределения |
|
1 |
количество инцидентов с |
Нормальный |
а = 103,07 σ =13,03 |
|
2 |
количество инцидентов с ИС |
Нормальный |
а = 203,82 σ = |
|
3 |
количество инцидентов с ПО |
Нормальный |
а = 168,86 σ = 39,40 |
|
4 |
количество инцидентов с |
Нормальный |
а = 67,86 σ = 9,67 |
|
5 |
количество инцидентов с БД |
Нормальный |
а = 34,86 σ = |
|
6 |
количество инцидентов с |
Пуассона |
a=1,83 |
|
7 |
время устранения инцидента |
Показательный |
λ = 0,53 |
|
8 |
время между инцидентами |
Показательный |
0,49 |
|
9 |
затраты на аутсорсинг |
Нормальный |
а = 3567,12 σ = 275,59 |
|
10 |
провести доп. Диагностику |
Бернулли |
P=0,26 |
|
11 |
затраты на диагностику |
Нормальный |
а = 700,07 |
|
12 |
материальные затраты |
Нормальный |
а = 337,05 |
|
13 |
затраты на модификацию ПО |
Показательный |
λ = 3,371 |
7. Разработка и описание математических моделей фрагментов
процесса
Целью имитационного моделирования является определение совокупная
стоимость ИТ сервиса отдела «Управление инцидентами».
Общая формула определения совокупной стоимости ИТ-сервиса выглядит
следующим образом:
=Premzat+Koszat (1);
где StoimIT -это затраты связанные компьютерное, телекоммуникационное
оборудование, оборудование АСУТП;прямые затраты;косвенные затраты.
Прямые и косвенные затраты также имеют свою градацию, и рассчитываются
следующим образом:
=Oborzat+POzat+Obslzat+Zarbzat (2);
где Oborzat -это затраты на оборудование,
включающие затраты на материальные активы (компьютерное, телекоммуникационное
оборудование, оборудование АСУТП).
POzat
— затраты на нематериальные активы, включающие в себя собственное программное
обеспечение, лицензии;
Obslzat
-затраты на устранение инцидента;
Zarbzat-
затраты на ИТ-персонал.
Koszat=Sboizat+Obychzat+NexPrzat+ Zarbzat (3)
где Sboizat -потери от сбоев и простоев;
Obychzat- затраты связанные с нехваткой знаний у сотрудников для решения
инцидента (затраты на обучение);
NexPrzat — затраты связанные с нехваткой персонала.
Zarbzat-
затраты на ИТ-персонал.
Расчет суммарных потерь от простоев.
Для каждой Учетной единице суммируются простои по категориям воздействия
на бизнес. Полученные суммы перемножаются на цену часа простоя каждой
категории, которая определена заранее и согласована с бизнесом. Полученные
произведения складываются по всем категориям для каждой ИТ-услуги.
При расчете стоимости сервиса также необходимо рассчитывать стоимость 1
рабочего места.
Учет стоимости ИТ-сервиса дает:
1) значительно более разнообразную информацию для управления
затратами, нежели модель прямых затрат. Во-первых, становится известной
загрузка ресурсов ИТ-службы. Для сотрудников учитываются человеко-часы работ,
для ресурсов инфраструктуры ИТ — процент загрузки мощностей, исходя из принципа
«узкого места». Эти показатели можно представить не только суммарно, но и в
расчете на единицу измерения ИТ-услуги. Тем самым упрощается прогнозирование
момента, когда даже простое сохранение качества существующих ИТ-услуг потребует
наращивания ресурсов ИТ-службы. Более того, можно с большой степенью
уверенности указать, какие именно дополнительные ресурсы потребуются.
2) исходные данные для расчета влияния повышения качества ИТ-услуги
на требования к ресурсам для ее сопровождения и, соответственно, на затраты
ИТ-службы. В частности, при расширении согласованного времени обслуживания
услуги электронной почты с 8*5 до 24*7, дополнительные требования к ресурсам
рассчитываются следующим образом. В ресурсы включается дополнительная смена
Help Desk. Далее, по таблице видов деятельности и привязке ресурсов к видам
деятельности выясняется, какие специалисты необходимы для сопровождения
электронной почты. Уточняется, какие виды деятельности могут осуществляться
удаленно, для остальных устанавливается посменное дежурство инженеров. Сумма
затрат на посменное дежурство операторов и инженеров составит дополнительные
затраты.
) становится возможным распределение затрат на ИТ-услуги по
подразделениям и пользователям, потребляющим эти услуги. Для каждого
подразделения оценивается число единиц потребления ИТ-услуги, что позволяет
определить долю затрат на услугу, которую должно компенсировать данное
подразделение. Это особенно важно для аутсорсинга или внутреннего хозрасчета
ИТ-службы, поскольку становится базой для экономически оправданной тарификации
услуг. Мало того, поскольку по стандартам модели ITSM в записи инцидента
обязательно указывается пользователь, у которого был прерван сервис, при
необходимости можно рассчитывать затраты на отдельных пользователей.
имитационный
модель бизнес инцидент
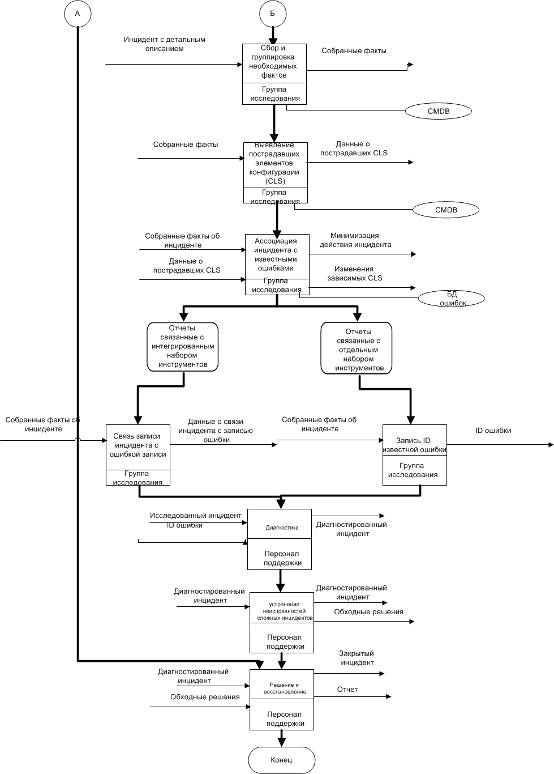
8. Разработка и описание моделирующих алгоритмов для
реализации программ имитационной модели
.1 Разработка моделирующих алгоритмов
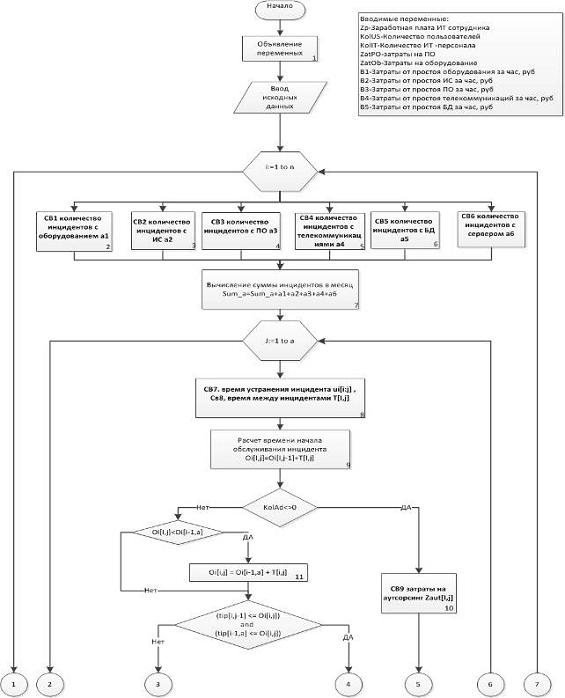
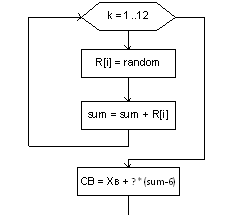
Рисунок 6 — Моделирующий алгоритм
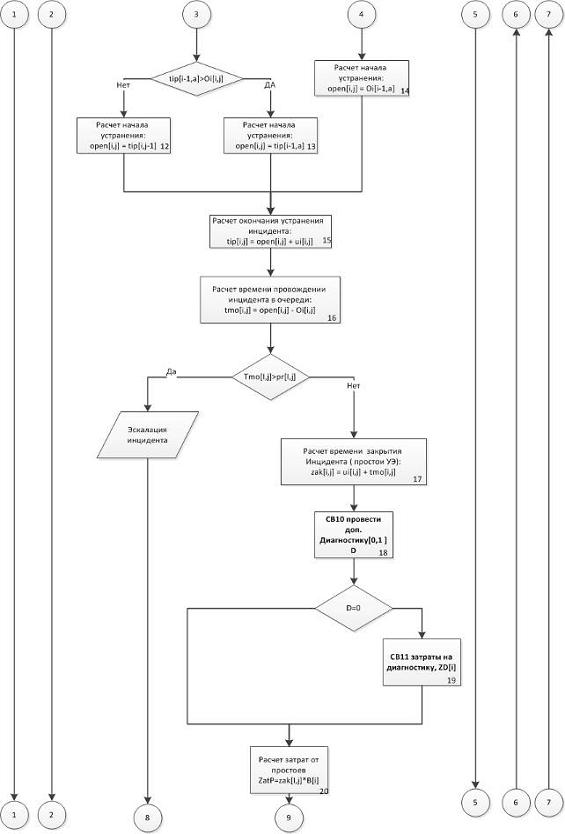
Рисунок 6 — Моделирующий алгоритм (продолжение)
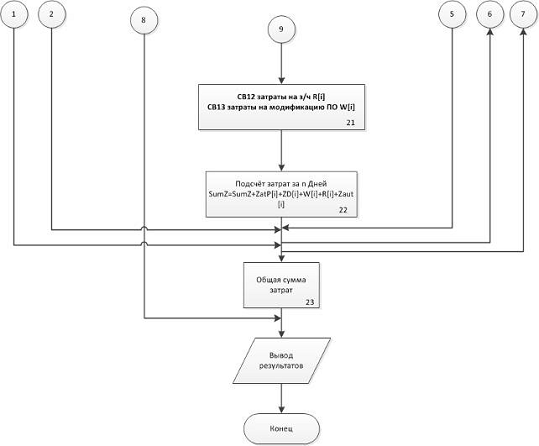
Рисунок 6 — Моделирующий алгоритм (окончание)
Рисунок 7 — моделирующий
алгоритм генерации случайной величины, распределенной по показательному закону
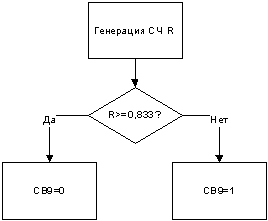
Рисунок 8 — Моделирующий
алгоритм генерации случайной величины, распределенной по закону Пуассона
Рисунок
9 — Моделирующий алгоритм генерации
случайной величины, распределенной по нормальному закону
8.2 Описание моделирующего алгоритма
1. Объявление переменных.
2-6. Генерируется случайные величины наступления инцидентов по
различным Учетным Элементам каждый день. n — количество дней в месяце,
a —
количество инцидентов в день.
. Рассчитываем общее количество инцидентов по УЭ за n дней
. В цикле от 1 до a генерируются случайные числа время между
поступления инцидентами и время устранения каждого инцидента, которые
распределены по показательному закону. С помощью параметров:
среднеквадратическое отклонение и математическое ожидание, смоделируем эти
величины.
. Производится расчет времени начала обслуживания инцидента.
. Если количество сотрудников равно 10, то инцидент
рассматривается сторонней фирмой. Генерируется случайная величина затрат на
аутсорсинг по устранения инцидента.
. Если поступления инцидента меньше времени поступления
последнего инцидента в предыдущий день, то поступление равно увеличению времени
последнего инцидента в предыдущий день на величину T, сгенерированную раннее.
. Если время окончания предыдущего инцидента больше времени
поступления нового, тогда новый инцидент начинает выполняться после того, как
выполниться предыдущий.
. Если в предыдущий день остался невыполненный инцидент, то новый
начинает выполняться после его окончания.
. Если время окончания последнего инцидента меньше или равно
времени поступления нового, тогда новый инцидент начинает выполняться сразу,
как только поступил.
. Производится расчет окончание устранения инцидентов. Оно равно
сумме времени начала выполнения и времени устранения инцидента.
. Рассчитывается время провождения инцидента в очереди.
. Если время провождения заявки в очереди больше установленного
лимита, то инцидент посылается на следующий уровень поддержки, иначе
рассчитывается время закрытия инцидента с учетом устранения инцидента и
ожидания инцидента в очереди.
. Генерируется случайная величина на проведению дополнительной
диагностики, которая имеет значение вероятности наступления того или иного
события, моделируется значение 0 или 1.
. Если получено значение 1, то генерируется случайная величина
затрат на дополнительную диагностику.
. Рассчитывается затраты от простоев.
. Генерируются случайные величины затрат на запасные части
аппаратного обеспечения и затрат на модификацию ПО.
. Рассчитывается сумма затрат по устранению инцидентов за n дней.
. Рассчитывается общая сумма затрат
. Вывод результатов моделирования.
На рисунке 7 представлена генерация случайной величины, распределенной по
показательному закону.
. Генерируется равномерно-распределенная случайная величина на отрезке
[0,1].
2. Вычисляется
значение по формуле
На рисунке 8 представлена генерация случайной величины, распределенной по
закону Пуассона.
. Вычисляется вероятность p = а/n,
где а — параметр распределения,
. Генерируется равномерно-распределенная случайная величина на
отрезке [0,1].
. Если СВ меньше p,
тогда она увеличивается на 1.
На рисунке 9 представлена генерация случайной величины, распределенной по
нормальному закону.
. Генерируется равномерно-распределенная случайная величина на
отрезке [0,1].
2. Вычисляется
. — нормально-распределенные
числа.
. Нормально-распределенные
числа с нужными параметрами
9. Разработка компьютерных программ моделирования
бизнес-процесса
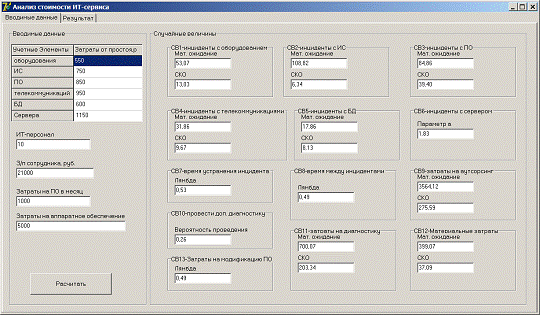
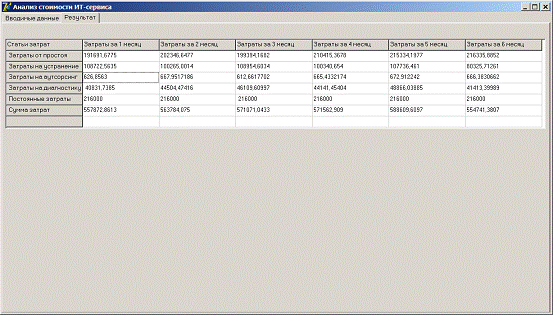
После запуска программы Анализ стоимости ИТ-сервиса необходимо ввести
исходные данные и случайные величины с параметрами распределения, по которым
будут производиться расчет показателей:
· Затраты от простоя;
· Затраты на устранение;
· Затраты на аутсорсинг;
· Затраты на диагностику;
· Постоянные затраты.
Рисунок 9 — Ввод исходных данных в таблицу
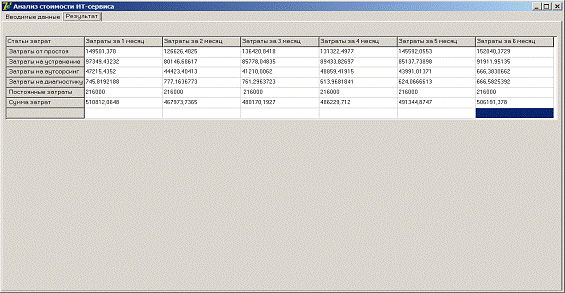
Рисунок 10 — Вывод результатов
На основе полученных данных можно выявить, общую стоимость затрат по
обслуживанию инцидентов за каждый месяц. С помощью параметров можно
регулировать затраты на персонал и рабочие материалы, количество времени
необходимое для решения инцидента, количество инцидентов, затраты от простоя по
Учетным Элементам. Производя несколько экспериментов, можно выявить, сколько
требуется времени, средств и людей для обслуживания инцидентов.
Листинг части программы генерации случайных величин.
Генерация случайной величины распределенной по нормальному закону:
sum,mat,sko:real;
a1:real;
R:array [1..12] of real;:= StrToFloat(LabeledEdit5.Text);:=
StrToFloat(LabeledEdit6.Text);:=0;j:=1 to 12
do[j]:=random;:=sum+L[j];;:=mat1+sko1*abs(sum-6);
Генерация случайной величины распределенной по показательному закону:
,ui:real;:=
StrToFloat(LabeledEdit16.Text);:=random;:=-ln(f)/lmb;;
Генерация случайной величины распределенной по закону Пуассона:
:= StrToFloat(LabeledEdit15.Text);:=100;:=mat/n;:=0;i:=1 to
100 do[i]:=random;R[i]<P then a6:=a6+1
end;
Генерация случайной величины распределенной по закону Бернулли:
begin:=StrToFloat(LabeledEdit17.Text);:=random;(N < P) or
(N = P) then D:=1 D:=0;;
10. Постановка и разработка оптимизационных задач
функционирования моделируемого бизнес-процесса
Основной задачей оптимизации является снижение затрат ИТ-сервиса
(сопровождение инцидентов) при сохранении должного уровня качества.
=Premzat+Koszat min
Для этого требуется оптимизировать ИТ-ресурсы. Под этим понимают:
§ упрощение инфраструктуры- формирование динамичной
инфраструктуры, более простой в управлении и модернизации, менее дорогой в
эксплуатации;
§ сокращение затрат — максимально эффективно использовать
ИТ-ресурсы и повысить общую производительность;
§ облегчение управления.
Около 60% ИТ-расходов отдела направляются на поддержку эксплуатации,
управление системами, их техническое сопровождение и текущие улучшения.
Мониторинг и контроль современных многоуровневых приложений сложная задача.
Огромное количество времени тратится непродуктивно, на процедуры отслеживания и
решения проблем вручную.
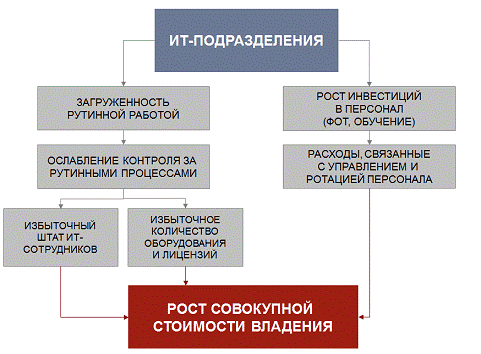
Основной причиной роста ИТ-затрат является: загруженность рутинной
работой, избыточный штат ИТ-сотрудников, избыточное количество оборудования и
лицензий, рост инвестиций в персонал, расходы, связанные с управлением и
ротацией персонала и т.д.
Рис.11
SVT (Sickness, Vacation, Training) — коэффициент отсутствия сотрудника на
месте, обычно колеблется от 15% до 25%. Для поддержания сервиса своими силами
необходимо привлечение SVT (%) дополнительных инженеров
Для понижения затрат на обслуживания инцидентов предлагается:
) удаленное разрешение инцидентов силами Service Desk.
Большинство инцидентов (45%) требует от специалиста выхода на место инцидента.
Внедрение ИС Service Desk позволяет удаленно разрешать инциденты методом
консультаций конечных пользователей и методами удаленного администрирования.
Это позволит сократить затраты на устранение инцидентов, сократить время
решения одного инцидента (25%) и следовательно сократить затраты от простоев.
Предположим, что
o Штат ИТ-службы компании 30 человек
o Средняя заработная плата ИТ-специалиста 21 000 рублей
o Количество пользовательских рабочих мест в компании 1500
o Среднее количество заявок по инцидентам 300
o Среднее время, затрачиваемое инженером на закрытие одного
инцидента 2 часа тогда
o стоимость обслуживания 1 рабочего места в месяц составляет:
(30х21 000)/1500=420 рублей
o Количество заявок, требующих выхода на место инцидента
составляет: 300х0,45=135
o Экономия времени при внедрении SD на решение одного инцидента составляет 2х0,25=0,5 часа
o Экономия времени по всем инцидентам за месяц составляет
135х0,5=67,5 часа
o Час работы специалиста стоит: 21000/22/8=120 рублей
o Экономия времени за месяц стоит 120*67,5= 8100 рублей
o С другой стороны, сокращается время простоев.
,5 *800=54100 рублей.
11. Решение поставленных оптимизационных задач. Получение
результатов моделирования
Рис.12 Эксперимент
По данным зарубежных ИТ-аналитиков 45% происходящих на рабочих местах
пользователей инцидентов требуют выхода инженера на место инцидента для сбора
информации об имуществе, его конфигурации, подключениях к сети, установленном
ПО и т.п. Если эта информация будет доступна инженеру со своего рабочего места,
то общие затраты от простоев инцидента сокращаются. Это достигается путем
автоматизация деятельности, внедрения системы Service Desk.
После проведения эксперимента по оптимизации затрат от простоев за счет
уменьшения времени на устранение инцидентов, общие затраты ИТ-сервиса
уменьшились в среднем на 12%, что в абсолютном значении составило 63100руб.
Разрабатывается план экспериментов с моделью для достижения поставленной
цели. При необходимости используют отсеивающий или оптимизирующий эксперименты.
12. Технико-экономическая интерпретация результатов
моделирования
Как построить оптимизированную инфраструктуру?
Целью оптимизации является превращение ИТ-инфраструктуры в полностью
оптимизированную, тесно интегрированную среду. Процесс оптимизации любой
конкретной инфраструктуры следует рассматривать как непрерывный ряд изменений
на пути статичной и негибкой инфраструктуры к полностью виртуализированной и
интегрированной. Никаких начальных или конечных точек оптимизации не
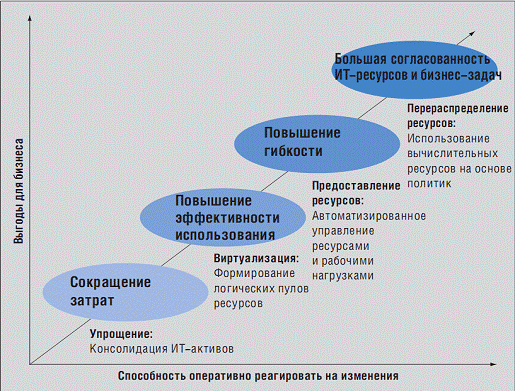
существует, однако можно выделить четыре ее отдельных этапа:
• Упрощение -консолидация и сокращение количества серверов, систем
хранения и других ИТ-ресурсов, позволяющие уменьшить сложность
ИТ-инфраструктуры и затраты на ее обслуживание и поддержку. Добиться этого
можно только путем внедрения технологий виртуализации ресурсов и их выделения
различным задачам.
• Виртуализация — объединение ИТ-активов в логические пулы ресурсов,
которые могут выделяться различным задачам, таким как обработка, хранение и
ввод/вывод. Организация логических разделов и/или кластеризация серверов
обеспечивают как максимальную гибкость, так и превосходные уровни надежности и
готовности. В конечном итоге виртуализация повышает и оптимизирует степень
использования ИТ-активов.
• Предоставление ресурсов -автоматизированное, гибкое и динамичное
выделение ИТ-активов конкретным задачам с использованием технологий управления
ресурсами и рабочей нагрузкой. Это позволяет повысить общую гибкость и
сократить расходы на внедрение, упрощая и ускоряя процедуры включения в
инфраструктуру новых ИТ-ресурсов.
Кроме того, автоматизированное выделение ресурсов повышает уровень
готовности и позволяет сократить время отклика. Этот этап также предусматривает
автоматизацию задач конфигурирования и технического сопровождения.
Кроме того, может быть внедрена технология автоматизированного
обнаружения и локализации «узких мест», снижающих производительность, чтобы
быстрее устранять подобные проблемы.
• Перераспределение ресурсов- обеспечение соответствия ИТ-инфра структуры
приоритетам бизнеса и реализация модели вычислений на базе политик. ИТ-ресурсы
могут распределяться автоматически, в соответствии с правилами, определяемыми
потребностями бизнеса. Таким образом, можно добиться того, чтобы ИТ-ресурсы
всегда распределялись с учетом приоритетов организации.
Рис.13 Оптимизация инфраструктуры
Преимущества оптимизированной ИТ-среды.
Оптимизированные ИТ-инфраструктуры отделяют приложения от ресурсов,
необходимых для выполнения этих приложений. Больше нет необходимости выделять
весь сервер или все устройство хранения одному приложению. В рамках динамичной
инфраструктуры множество приложений могут совместно использовать общий пул
ИТ-ресурсов. Функциональность приложения выражается в виде простых в
управлении, тесно интегрированных, модульных сервисных компонентов, которые
взаимодействуют через четко определенные открытые интерфейсы. Барьеры между
приложениями исчезают, размываются информационные островки, и обеспечивается
максимально гибкое использование ресурсов.
Имея возможность использовать прежде простаивавшие вычислительные мощности,
компании могут быстрее расширять свой бизнес и предлагать дополнительные
сервисы, которые прежде были невозможны. Например, учреждения сферы финансовых
услуг могут осуществлять углубленный технический анализ различных финансовых
инструментов, чтобы определять самые прибыльные варианты инвестиций. Благодаря
гибкости, которую дает самоуправляемая и саморегулируемая инфраструктура,
предприятия могут более оперативно развертывать новые функциональные
возможности, обеспечивая ускоренное получение экономического эффекта от
введения новых сервисов.
Кроме того, гибкие, оптимизированные ИТ-инфраструктуры позволяют
организациям внедрять модели вычислений на основе политик, с автоматическим
распределением ресурсов в соответствии с бизнес приоритетами на основе четко
определенных правил и политик. Это позволяет использовать ИТ-ресурсы с учетом
приоритетов бизнеса, а также более оперативно и экономически эффективно
реализовать инициативы, способствующие успешной реализации бизнес-стратегий.
Заключение
В результате построения имитационной модели бизнес-процесса «Управление
инцидентами» была спрогнозирована общая сумма затрат по обслуживанию инцидентов
за 6 месяцев. При оптимизации бизнес процесса затраты были уменьшены примерно
на 12%, снижено средне-месячное время простоя работы каждого из сотрудников на
22 минуты
Удаленное разрешение части инцидентов при первом обращении силами Service
Desk дает снижение среднемесячного времени простоя каждого из сотрудников на
~1,25 часа.
В случае оптимизации числового критерия формулируют гипотезы о выборе
наилучших вариантов структур моделируемой системы или режимов ее
функционирования, определяют диапазон значений параметров (режимов
функционирования) модели, в границах которых осуществляется поиск оптимального
решения.
Список используемой литературы
1. Курс
лекций «Имитационное моделирование экономических процессов»
2. Курс
лекций «Теория вероятностей и математическая статистика»
. Димов
Э.М., Богданова Е.А. Методическое пособие к курсовой работе на тему
«Имитационное моделирование бизнес-процессов компании» для студентов
специальности 080801 (прикладная информатика в экономике) — Самара: ПГАТИ,
2007. — 31 с., ил.
. Гмурман
В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов.
Изд.7-е, стер. — М.:Высш.шк., 2000. — 479 с.
. Димов
Э.М., Маслов О.Н., Пчеляков С.Н., Скворцов А.Б. Новые информационные
технологии: подготовка кадров и обучение персонала. Часть 2. Имитационное
моделирование и управление бизнес-процессами в инфокоммуникациях. Научное
издание. — Самара: «Издательство СамНЦ РАН», 2008. — 350 с.: ил.
КУРСОВАЯ РАБОТА
по дисциплине Перспективные информационные системы в экономике
на тему «Имитационное моделирование бизнес-процессов организации»
Содержание
Введение
. Цели и задачи имитационного моделирования
2. Выбор, обоснование, схема и описание бизнес-процесса организации
3. Определение состава исходных данных для моделирования
. Статистическое исследование бизнес-процесса
. Идентификация законов распределения случайных величин
6. Разработка и описание моделирующего алгоритма для реализации программы имитационной модели
. Разработка компьютерной программы моделирования бизнес-процесса
8. Технико-экономическая интерпретация полученных результатов
Заключение
Список используемых источников
Введение
В исследовании операций широко применяются как аналитические, так и статистические модели. Каждый из этих типов имеет свои преимущества и недостатки. Аналитические модели более грубы, учитывают меньшее число факторов, всегда требуют каких-то допущений и упрощений. Зато результаты расчета по ним легче обозримы, отчетливее отражают присущие явлению основные закономерности. А, главное, аналитические модели больше приспособлены для поиска оптимальных решений. Статистические модели, по сравнению, с аналитическими, более точны и подробны, не требуют столь грубых допущений, позволяют учесть большое (в теории — неограниченно большое) число факторов. Но и у них — свои недостатки: громоздкость, плохая обозримость, большой расход машинного времени, а главное, крайняя трудность поиска оптимальных решений, которые приходятся искать «на ощупь», путем догадок и проб.
Наилучшие работы в области исследования операций основаны на совместном применении аналитических и статистических моделей. Аналитическая модель дает возможность в общих чертах разобраться в явлении, наметить как бы контур основных закономерностей. Любые уточнения могут быть получены с помощью статистических моделей.
Имитационное моделирование — метод, позволяющий строить модели <#»justify»>Предметом исследования данной работы являются процессы, проходящие в ГБУ «Центр социального обслуживания граждан пожилого возраста и инвалидов городского округа Чапаевск». Более подробно рассматривается бизнес-процесс «Предоставление клиенту социального обслуживания на дому», производится его имитационное моделирование.
1. Цели и задачи имитационного моделирования
Свою практическую деятельность ГБУ «Центр социального обслуживания граждан пожилого возраста и инвалидов городского округа Чапаевск» начало с 01.02.1991 г.
Целью деятельности Центра является: осуществление на закрепленной территории организационной, практической и методической деятельности по социальному обслуживанию и оказанию социальных услуг гражданам (семьям), оказавшимся в трудной жизненной ситуации.
Главные принципы в работе: доброжелательность, гуманность, адресность, универсальность, максимизация социальных ресурсов, конфиденциальность и толерантность.
Задачами деятельности Центра являются:
¾организация и предоставление гарантированных и дополнительных социальных услуг гражданам пожилого возраста, инвалидам, попавшим в сложную жизненную ситуацию;
¾выявление граждан, проживающих на обслуживаемой Учреждением территории и нуждающихся в гарантированных социальных услугах;
¾оказание социальных услуг постоянного, временного или разового характера лицам, нуждающимся в социальном обслуживании;
¾осуществление трудовой реабилитации клиентов учреждения в цехах, мастерских, и иных структурных подразделения Учреждения, осуществляющих трудотерапию;
¾организация срочной социальной помощи;
¾содействие лицам с ограничением жизнедеятельности (в том числе инвалидам) в получении медико-социального освидетельствования, реабилитационных мероприятий, технических средств реабилитации и протезно-ортопедических изделий.
Основными функциями Центра являются:
¾предоставление социальной поддержки;
¾оказание социально-бытовых, социально-медицинских, психолого-педагогических, социально-правовых услуг и оказание материальной помощи;
¾проведение социальной адаптации граждан, находящихся в трудной жизненной ситуации.
Центр социального обслуживания предоставляет следующие социальные услуги:
¾Отделение социального обслуживания на дому предназначается для временного (до 6 месяцев) или постоянного оказания гражданам, частично утратившим способность к самообслуживанию и нуждающимся в посторонней поддержке, социально — бытовой помощи в надомных условиях. Обслуживание на дому граждан осуществляется путем предоставления им, в зависимости от степени и характера нуждаемости, социально — бытовых, консультативных и иных услуг, входящих в федеральный и территориальный перечни гарантированных государством социальных услуг, оказываемых государственными и муниципальными учреждениями социального обслуживания, а также оказания, по их желанию, дополнительных социальных услуг, не входящих в эти перечни.
¾Специализированное отделение социально — медицинского обслуживания на дому предназначается для временного (до 6 месяцев) или постоянного социально — бытового обслуживания и оказания доврачебной медицинской помощи в надомных условиях гражданам, частично или полностью утратившими способность к самообслуживанию и страдающими тяжелыми заболеваниями, в том числе онкологическими в поздних стадиях течения, психическими расстройствами в стадии ремиссии, туберкулезом за исключением активной формы, являющимися противопоказанием к принятию в отделение социального обслуживания на дому.
¾Отделение срочного социального обслуживания предназначается для оказания гражданам, остро нуждающимся в социальной поддержке, неотложной помощи разового характера, направленной на поддержание их жизнедеятельности.
¾Оказание психологической помощи включает в себя социально-психологическое консультирование, психологическую диагностику и обследование личности, психологическое консультирование, психологическую коррекция, психологическую помощь (в том числе по телефону);
¾Оказание юридической помощи включает в себя консультирование по вопросам, связанным с правом граждан на социальное обслуживание в государственной и негосударственной системах социальных служб и защиты своих интересов, оказание помощи в оформлении документов, содействие в осуществлении по отношению к гражданам пожилого возраста инвалидам мер социальной поддержки и получении преимуществ, установленных действующим федеральным и региональным законодательством, содействие в получении юридической помощи, консультаций по социально-правовым вопросам и иных правовых услуг, содействие в получении бесплатной помощи адвоката в порядке, установленном действующим законодательством, оказание других форм срочного социального обслуживания, обусловленных региональными особенностями и предусмотренных территориальным перечнем гарантированных государством социальных услуг.
¾Социально-реабилитационное отделение является полустационарным структурным подразделением Центра и предназначается для социально — бытового, культурного, медицинского обслуживания граждан, сохранивших способность к самообслуживанию и активному передвижению, организации их отдыха, привлечения к посильной трудовой деятельности и поддержания активного образа жизни.
В связи с этим, целью имитационного моделирования является анализ состояния и перспектив совершенствования предоставляемых социальных услуг ГБУ «Центр социального обслуживания граждан пожилого возраста и инвалидов городского округа Чапаевск».
Задачами являются:
¾анализ делопроизводственной и специальной документации социального учреждения;
¾сбор и анализ информации о лицах, обращающихся в Центр и об оказании им социальных услуг;
¾сбор и анализ информации о социальном учреждении и обслуживающем персонале;
¾определение порядка работы с документами;
¾предложения направлений и методов совершенствования социальных услуг.
. Выбор, обоснование, схема и описание бизнес-процесса организации
В рамках курсового проекта выбран один из основных бизнес-процессов организации «Предоставление клиенту социального обслуживания на дому». Выбранный бизнес-процесс позволяет систематизировать работу всех процессов организации, проанализировать работу этих процессов и сделать соответствующие выводы о моделировании и исследовании данного процесса.
Рассмотрим подробно выбранный бизнес-процесс «Предоставление клиенту социального обслуживания на дому» (рис.1).
Бизнес-процесс начинается с обращение потенциального клиента или его законного представителя в учреждение, регистрацию обращения, оформление заявления потенциального клиента на имя руководителя учреждения о рассмотрении возможности предоставления социального обслуживания на дому, которое является основанием для проведения акта обследования материально-бытового положения, ознакомление с нормами и правилами предоставления социального обслуживания на дому, консультирование потенциального клиента, клиента или его законного представителя по вопросам предоставления социального обслуживания на дому.
Учреждение обеспечивает потенциальному клиенту условия для заключения Договора, в соответствии с действующим законодательством, потребностями и особенностями его жизненной ситуации.
Неотъемлемым приложением к Договору является «Перечень согласованных социальных услуг» с указанием наименований социальных услуг, периодичности предоставления, кратности оказания социальных услуг на дому, согласованных с клиентом.
Предоставление социального обслуживания на дому осуществляется только при выполнении клиентом норм и правил предоставления социального обслуживания на дому.
Рис.1. Бизнес-процесс «Предоставление клиенту социального обслуживания на дому»
3. Определение состава исходных данных для моделирования
бизнес процесс моделирование алгоритм
Для разработки имитационной модели процесса «Предоставление клиенту социального обслуживания на дому» определим состав исходных данных.
К исходным данным относятся детерминированные и случайные величины, оказывающие основное влияние на рассматриваемый бизнес-процесс.
Исходя из бизнес-процесса, определим состав исходных данных для моделирования. Процесс начинается с поступления от клиента обращения и документов на предоставления социального обслуживания на дому. Время между поступлением обращений носит случайный характер. После получения обращения отдел социального обслуживания на дому начинает проверку документов на соответствие критериям. Время для проведения оценки индивидуальной нуждаемости неодинаково для различных обращений. В том случае, если принято решение о предоставлении социальных услуг, отдел социального обслуживания на дому начинает рассматривать заявление клиента. Время составления заявления о предоставлении социального обслуживания на дому носит случайный характер. Исходя из информации, содержащейся в заявлении от клиента, юридический отдел составляет договор. Приложением к Договору идет Перечень согласованных социальных услуг с клиентом. Время согласования Перечня социальных услуг носит случайный характер. После этого отдел бухгалтерии предъявляет расчетный счет оказанных услуг. Время между подписанием Договора и получением квитанции об оплате социальных услуг клиентом различно.
К детерминированным данным относятся следующие: число каналов , доход от обслуживания одного обращения, издержки обслуживания одного обращения, период работы системы .
К случайным величинам относятся следующие:
¾среднее время между соседними обращениями ;
¾среднее время проведения оценки индивидуальной нуждаемости ;
¾среднее время составления заявления клиентом ;
¾среднее время заключения Договора;
¾среднее время формирования Перечня социальных услуг ;
¾среднее время оплаты социальных услуг .
. Статистическое исследование бизнес-процесса
С целью выявления законов распределения случайных факторов, влияющих на работу подразделения, и оценки параметров законов распределения были проведены статистические наблюдения случайных величин, число которых составило 100.
Исходя из описанного выше бизнес-процесса целесообразно выделить следующие случайные величины, оказывающие влияние на эффективность работы сотрудников Центра социального обслуживания:
¾время между поступлением обращений (СВ1);
¾продолжительность проведения оценки индивидуальной нуждаемости (СВ2);
¾продолжительность составления заявления клиентом (СВ3);
¾продолжительность заключения Договора (СВ4);
¾продолжительность формирования Перечня социальных услуг (СВ5);
¾время между подписанием Договора и получением квитанции об оплате социальных услуг клиентом (СВ6).
Для построения модели необходимо найти законы распределения этих случайных величин. Статистические данные по двум, рассматриваемым в данной работе случайным величинам, приведены в следующем разделе.
. Идентификация законов распределения случайных величин
В рамках курсового проекта проведем идентификацию законов распределения случайных величин выбранного бизнес-процесса «Предоставление клиенту социального обслуживания на дому».
Рассмотрим случайную величину — время между поступлением обращений (СВ1). На основе полученной репрезентативной выборки необходимо сделать предположение о законе распределения исследуемой случайной величины, рассчитать его основные параметры и проверить выдвинутую гипотезу о виде закона распределения.
Проверка статистической гипотезы осуществляется с использованием электронной таблицы Microsoft Excel. Обрабатываемая дискретная выборка случайных чисел преобразуется в интервальный ряд, рассчитываются частоты попадания данной случайной величины в полученные интервалы и определяются числовые характеристики эмпирического распределения.
В табл.1 приведены статистические данные случайной величины времени между поступлением обращений (час).
В качестве первого приближения разбиения имеющейся выборки на интервалы используется так называемая формула Стерджесса:
,
где — число интервалов;
— число единиц совокупности.
Для нашего случая в соответствии с данной формулой получаем число интервалов, равное 8.
Таблица 1
601037324816253449656338459121430917122449105523132324814191740293563243239254133423523362047951161034101015253781159141616191572310275110817111419481657122551173618391716289105616161327151322
Рассчитанные значения частот попадания случайной величины в каждый из интервалов ; , а также найденные значения дисперсии и выборочной средней представлены в табл.2.
Таблица 2
Частоты, выборочные средние и дисперсия случайной величины времени между поступлением обращений
№Частота Частость, Центральный интервал, Среднее выборочное, Отклонение от среднего, Квадрат отклонения, Дисперсия, 1714,25280,2810,63297,5-15,73247,516930,32214,2521,5210,2117,88375,38-8,4871,951511,01321,528,75150,1525,13376,88-1,231,5222,79428,7536110,1132,38356,136,0236,21398,3153643,2580,0839,63317,013,27176,031408,21643,2550,560,0646,88281,2520,52420,972525,81750,557,7560,0654,13324,7527,77771,034626,2857,756550,0561,38306,8835,021226,236131,13Итого1002635,75235,54
Выборочная средняя .
Дисперсия .
СКО =15,354.
Параметр .
Полученное распределение наглядно иллюстрирует гистограмма частости интервального ряда, показанная на рис.2.
Рис.2. Гистограмма распределения частости случайной величины , времени между поступлением обращений
Вид гистограммы на рис.2 позволяет предположить, что исследуемая случайная величина подчиняется экспоненциальному закону распределения с параметром .
Для проверки данной гипотезы воспользуемся критерием согласия (критерий Пирсона). При этом необходимо оценить значение суммы вида
,
где — частота эмпирического распределения в интервале ;
— частоты теоретического распределения в интервале ;
— число наблюдений;
— теоретическая вероятность попаданий значений случайной величины в заданный интервал;
— число интервалов наблюдения.
Значения эмпирической вероятности определяются отношением частоты попадания значений случайной величины в заданный интервал к общему числу наблюдений.
Чем меньше различаются между собой значения теоретической и эмпирической вероятностей, тем меньше значение критерия .
Вычисленные теоретические вероятности попадания значений исследуемой случайной величины в заданные интервалы приведены в табл.2; а соответствующие данным таблиц 2 и 3 значения критерия — в табл.4.
Таблица 3
Теоретические вероятности для случайной величины
№1714,25-0,27-0,540,76680,58240,1844214,2521,5-0,54-0,820,58240,44230,14321,528,75-0,82-1,090,44230,33600,1064428,7536-1,09-1,370,33600,25520,080853643,25-1,37-1,640,25520,19380,0614643,2550,5-1,64-1,920,19380,14720,0466750,557,75-1,92-2,190,14720,11180,0354857,7565-2,19-2,470,11180,08490,0269
Сумма значений .
Приведенное в табл.4 значение необходимо сравнить с критическим значением . Найденным по таблицам распределения Стьюдента.
Таблица 4
Результаты расчета значений
№1280,184418,43889,5691,422210,1414,00477,048,933150,106410,63694,3619,044110,08088,07902,928,53580,06146,13621,863,47660,04664,66061,341,79760,03543,53982,466,05850,02692,68862,315,34
Значение параметра .
Выбрав уровень значимости и учитывая, что в данном случае число степеней свободы , находим значение . Поскольку , был сделан вывод о том, что его значение попадает в область принятия данной статистической гипотезы. Следовательно, полученные данные о законе распределения рассматриваемой случайной величины (времени между поступлением обращений) не противоречат предположению о ее экспоненциальном распределении с параметром .
Проведем идентификацию законов распределения для следующей случайной величины — продолжительность проведения оценки индивидуальной нуждаемости (СВ2).
Значения случайной величины приведены в табл. 5 (час).
Таблица 5
1617209162221829121059311527703545151111191616335412810727293831113241251017171892559127115342231123011529923148711535811719422520773321177172344383866670402
Таблица 6
Частоты, выборочные средние и дисперсия
№Частота Частость, Центральный интервал, Среднее выборочное, Отклонение от среднего, Квадрат отклонения, Дисперсия, 11,012,3550,556,63364,38-12,26150,378270,29212,323,5160,1617,88286,0-1,011,0316,4323,534,8130,1329,13378,6310,24104,811362,48434,84660,0640,38242,2521,49461,712770,2854657,350,0551,63258,1332,741071,745358,72657,368,520,0262,88125,7543,991934,93869,8768,579,820,0274,13148,2555,243051,186102,36879,891,010,0185,3885,3866,494420,594420,59Итого1001888,75321,71
Выборочная средняя .
Дисперсия .
СКО =17,94.
Параметр .
Рис.3. Гистограмма распределения частости случайной величины
Таблица 7
Теоретические вероятности для случайной величины
№11,012,3-0,05-0,650,94840,52280,4256212,323,5-0,65-1,240,52280,28820,2346323,534,8-1,24-1,840,28820,15880,1293434,846-1,84-2,440,15880,08760,071354657,3-2,44-3,030,08760,04830,0393657,368,5-3,03-3,630,04830,02660,0217768,579,8-3,63-4,220,02660,01470,0119879,891,0-4,22-4,820,01470,00810,0066
Сумма значений .
Таблица 8
Результаты расчета значений
№1550,425642,564312,443,632160,234623,4620-7,462,373130,129312,93260,070,00460,07137,1286-1,130,18550,03933,92941,070,29620,02172,1659-0,170,01720,01191,19390,810,54810,00660,65810,340,18
Значение параметра .
Приведенное в табл.8 значение необходимо сравнить с критическим значением . Найденным по таблицам распределения Стьюдента. Выбрав уровень значимости и учитывая, что в данном случае число степеней свободы , находим значение . Поскольку , был сделан вывод о том, что его значение попадает в область принятия данной статистической гипотезы. Следовательно, полученные данные о законе распределения рассматриваемой случайной величины не противоречат предположению о ее экспоненциальном распределении с параметром.
Аналогично была проведена идентификация законов распределения для других случайных величин, в ходе которой получены следующие результаты:
¾продолжительность составления заявления клиентом (СВ3) — экспоненциальный закон распределения с параметром ;
¾продолжительность заключения Договора (СВ4) — экспоненциальный закон распределения с параметром ;
¾продолжительность формирования Перечня социальных услуг (СВ5) — экспоненциальный закон распределения с параметром ;
¾время между подписанием Договора и получением квитанции об оплате социальных услуг клиентом (СВ6) — экспоненциальный закон распределения с параметром .
6. Разработка и описание моделирующего алгоритма для реализации программы имитационной модели
Для проектирования модели используются данные о деятельности Центра социального обслуживания граждан пожилого возраста и инвалидов городского округа Чапаевск, а также информация об изменениях этих данных и максимально подробное описание всех операций, осуществляемых с ними сотрудниками организации. Недостаток такого рода сведений может привлечь за собой необходимость пересмотра самого способа построения модели.
Для описания работы Центра подходит математическая схема СМО. Для таких клиентов характерны три отличительные особенности:
¾имеется поток клиентов, желающих быть обслуженными;
¾имеются каналы обслуживания, которые обеспечивают удовлетворение обращений клиентов (в данном случае сотрудники Центра);
¾имеется определенный набор правил обслуживания клиентов.
Поскольку неизвестно, сколько целесообразно всего иметь сотрудников в Центре для обработки обращений, то число каналов обслуживания в модели должно быть переменным. Оно будет зависеть от соотношения между средним временем между поступлениями обращений и средним временем рассмотрения этих обращений, — поэтому необходимо учитывать эти случайные величины.
Следует помнить, что реальные процессы, протекающие в организации, все же слишком сложны, чтобы полностью и исчерпывающе их понять и описать. Возникшие проблемные ситуации связаны с практическим бесконечным числом элементов, переменных, параметров, ограничений и т.д., поэтому при моделировании необходимо поступить разумно и отбросить достаточно большую часть их характеристик, выделив лишь те особенности, которые позволяют воссоздать идеализированный вариант каждой проблемной ситуации. Следовательно, модель работы организации дает всегда упрощенное представление о фрагменте реального бизнеса; от того, насколько корректно сконструировано это представление, зависит степень адекватности модели и действительности.
Для имитационной модели вполне достаточно изложения общих принципов с указанием условных характеристик объекта исследования.
Так же необходимо знать, как будут вести себя клиенты, если им придется стоять в очереди.
При описании нашей СМО наиболее подходящим является режим ожидания «с неограниченным ожиданием».
Правило обслуживания состоит в том, что очередное обращение поступает в тот канал, который раньше других освободился. Так как в нашем случае режим неограниченного ожидания, то обращение может покинуть систему необслуженной в том случае, если время ожидания начала обслуживания превышает величину Ткон (период функционирования СМО).
Входными характеристиками модели являются:
¾число каналов ;
¾среднее время между соседними обращениями ;
¾среднее время проведения оценки индивидуальной нуждаемости ;
¾период работы системы ;
¾число случайных реализаций процесса ;
¾среднее время составления заявления клиентом ;
¾среднее время заключения Договора;
¾среднее время формирования Перечня социальных услуг ;
¾среднее время оплаты социальных услуг .
Выходной характеристикой модели является среднее число обслуженных обращений
В качестве показателя эффективности работы системы выберем среднюю прибыль:
,
где — чистая прибыль, полученная в результате обслуживания одного обращения;
— издержки обслуживания всех обращений, зависящих от числа каналов.
Если разделить обе части равенства на , получим формулу для нахождения показателя эффективности:
,
где — средняя относительная прибыль,
— функция числа каналов.
Основным вариантом функциональной зависимости является возрастающая зависимость с положительной второй производной. Отсюда следует:
.
Для расчета показателя эффективности будем использовать формулу:
.
В качестве критерия выбора неивыгоднейшей структуры СМО принимается оптимальное число каналов обслуживания, обеспечивающее максимум средней относительной прибыли:
,
где — наивыгоднейшее число каналов.
Количество клиентов за один рабочий день будет определяться в зависимости от времени прихода клиентов и времени обслуживания этих клиентов, но эта величина не может превышать максимальное количество клиентов. Клиент обслуживается в том случае, если он появился до окончания рабочего времени, и если время его обслуживания не будет превышать рамки рабочего времени.
В результате моделирования будет получено оптимальное количество сотрудников Центра, то есть такое, при котором прибыль данного отдела, следовательно, и организации в целом, станет максимальной при наименьших затратах на содержание данного отдела.
Представим моделирующий алгоритм в графической форме (рис.4). Графической формой представления моделирующих алгоритмов являются структурные схемы.
Рис.4. Обобщенная схема моделирующего алгоритма
Рассмотрим каждый из блоков моделирующего алгоритма в отдельности. В блоке 1 осуществляется ввод исходных данных. Блок 1а служит для проверки данных на соответствие какому-либо закону распределения. В блоке 2 осуществляется установка начальных значений параметров модели, то есть обнуление счетчиков и переменных. В блоке 3 производится моделирование системы, в которой возможны очереди клиентов, но нет отказа технических подсистем. В блоке 4 производится расчет критерия эффективности — средней относительной прибыли, являющейся основным результатом моделирования системы. Блок 5 позволяет по полученным результатам моделирования построить диаграммы распределения процесса предоставления социальных услуг в зависимости от числа сотрудников Центра, обслуживающих обращения.
Рассмотрим более подробно блок 3, в котором производится непосредственное моделирование системы. Обобщенная блок-схема представлена на рис. 5.
Моделирование начинается с обнуления значений времени поступления обращений — блок 1. Во 2 блоке счетчику цикла i присваивается значение 1. В блоке 3 проверяется условие . В данном случае цикл состоит из 100 итераций. Если условие блока 3 выполняется, в 4 блоке происходит моделирование по показательному закону случайной величины времени поступления обращений и увеличение значения данной переменной. В блоке 5 счетчик цикла увеличивается на 1, и осуществляется переход к блоку 3. Если условие блока 3 не выполняется, цикл завершается и в блоке 6 определяется среднее значение данной переменной. На этом заканчивается моделирование времени поступления клиентов, и начинается моделирование времени проведения оценки индивидуальной нуждаемости.
В блоке 7 происходит обнуление значений времени проведения оценки индивидуальной нуждаемости. Далее аналогично предыдущей переменной осуществляется моделирование среднего значения данной переменной, т.к. закон распределения такой же, как и в предыдущем случае. Значение параметра закона распределения берется из соответствующей ячейки параметров законов распределения. Моделирование проведения оценки индивидуальной нуждаемости в блоках 7-12. Далее моделирование времени составления заявления клиентом — блоки 13-18. Затем моделирование времени заключения Договора — блоки 19-24, времени формирования Перечня социальных услуг — блоки 25-30, времени оплаты социальных услуг — блоки 31-36. В блоке 37 проверяется окончание времени моделирования. Если условие блока выполняется, то происходит переход к блоку 3 и моделирование продолжается, если же нет, то полученные результаты фиксируются и моделирование завершается.
Рис.5. Обобщенная блок-схема алгоритма блока 3 «Моделирование системы»
. Разработка компьютерной программы моделирования бизнес-процесса
Имитационная модель, рассматриваемая в рамках курсового проекта, написана на языке программирования Delphi 7.- одна из самых мощных систем, позволяющих на самом современном уровне создавать как отдельные прикладные программы Windows, так и разветвленные комплексы, предназначенные для работы в корпоративных сетях и в Интернет. Это продукт, уникальным образом сочетающий высокопроизводительный компилятор, объектно-ориентированные средства визуального программирования и универсальный механизм доступа к базам данных.- это система визуального объектно-ориентированного программирования, позволяющая решать множество задач, в частности:
1.Создавать законченные приложения для Windows самой различной направленности, от чисто вычислительных и логических, до графических и мультимедиа.
2.Быстро создавать профессионально выглядящий оконный интерфейс для любых приложений, написанных на любом языке; интерфейс удовлетворяет всем требованиям Windows и автоматически настраивается на ту систему, которая установлена на компьютере пользователя, поскольку использует многие функции, процедуры, библиотеки Windows.
.Создавать мощные системы работы с локальными и удаленными базами данных любых типов; при этом имеются средства автономной отладки приложения с последующим выходом в сеть.
.Создавать многозвенные распределенные приложения, основанные на различных технологиях.
.Создавать приложения различных классов для работы в Интернет.
.И многое другое, включая создания отчетов, справочных систем, библиотек DLL, компонентов ActiveX.
Рассмотрим подробно процесс работы системы.
Работа пользователя с программой начинается с экранной формой «Ввод исходных данных» (рис. 6). В данной форме необходимо ввести исходные данные и задать необходимые параметры моделирования.
Рис.6. Форма «Ввод исходных данных»
Исходные данные вводятся в специальные поля. Нажатие на кнопки «Введите исходные данные» и «Параметры законов распределения» обнуляет значения специальных полей.
После ввода исходных данных с помощью кнопки «Моделировать» осуществляется непосредственное моделирование и получение выходных данных и открывается новая форма «Результаты моделирования» (рис. 7).
Рис.7. Форма «Результаты моделирования»
Из данной формы можно перейти в форму «Вывод результатов», нажав на кнопку «Рассчитать среднюю относительную прибыль» (рис. 8).
Возврат к форме «Ввод исходных данных» осуществляется с помощью нажатия на кнопку «Исходные данные».
Рис.8. Форма «Вывод результатов»
В результате работы имитационной модели получили следующие результаты — наибольшее значение средней относительной прибыли достигается, если обслуживанием обращений занимается 4 сотрудника Центра социального обслуживания.
. Технико-экономическая интерпретация полученных результатов
Программа, написанная в среде Borland Delphi 7, для моделирования бизнес-процесса «Предоставление клиенту социального обслуживания на дому» позволяет прослеживать интерпретацию полученного результата.
В основе интерпретации лежит процедура объяснения полученных результатов на основе принятой в исследовании концепции.
В задачи интерпретации входят: выявление объективного значения полученных результатов для оптимизации работы организации, а также смысла, т. е. значения для самого исследователя или заинтересованного в результатах исследования круга лиц.
В результате нескольких прогонов модели было выявлено, что с учетом всех исходных данных: максимальное количество клиентов, среднее время между поступлением обращений, среднее время обслуживания клиентов, продолжительность рабочего дня — был получен результат, который наглядно демонстрирует, каким должно быть оптимальное количество сотрудников Центра социального обслуживания, при котором прибыль отдела социального обслуживания на дому, следовательно, и организации в целом, станет максимальной при наименьших затратах на содержание данного отдела. И в результате проведенных исследований было выявлено, что оптимальное количество специалистов, работающих с клиентами должно быть равным 4.
Работу данной модели можно использовать для прогнозирования работы управления в будущем и на основании полученных приблизительных результатов делать выводы о результатах работы и принимать необходимые меры по улучшению показателей работы организации.
Заключение
В рамках данного курсового проекта разработана имитационная модель для применения в ГБУ «Центр социального обслуживания граждан пожилого возраста и инвалидов городского округа Чапаевск». Имитационная модель предназначена для моделирования бизнес-процесса «Предоставление клиенту социального обслуживания на дому».
При разработке имитационной модели были определены и обоснованы параметры имитационной модели, идентифицированы законы распределения случайных величин, разработан моделирующий алгоритм.
В результате выполнения данного курсового проекта были получены практические знания в области имитационного моделирования экономических процессов.
Был решен следующий круг задач: структуризация конкретного бизнес-процесса с позиции решения задач принятия управленческих решений в рамках современной экономической информационной системы; применение технологии компьютерного моделирования для решения конкретной задачи повышения эффективности управления бизнес-процессом.
Имитационное моделирование является одним из самых мощных, перспективных и эффективных инструментов моделирования бизнес-процессов, особенно в ситуациях, когда необходимо принимать обоснованные и целенаправленные решения в условиях неопределенности. Этот подход базируется на возможность моделирования проблемных ситуаций организаций в условиях экономической нестабильности и рисков. При этом руководству организации предлагается следовать принципу комплексного применения рационального и интуитивного анализа возникающих проблем, их раннему диагностированию и предупреждению.
Список используемых источников
1.Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. Изд.7-е, стер. — М.: Высшая школа, 2010. — 479 с.
2.Димов Э.М., Богданова Е.А. Методическое пособие к курсовой работе на тему «Имитационное моделирование бизнес-процессов компании» для студентов специальности 080801 (Прикладная информатика в экономике). — Самара: ПГАТИ, 2007. — 31 с.
.Димов Э.М., Маслов О.Н., Скворцов А.Б. Новые информационные технологии: Подготовка кадров и обучение персонала. Часть 1. Реинжиниринг и управление бизнес-процессами в инфокоммуникациях. Научное издание. — М.: ИРИАС, 2009. — 386 с.
.Кобелев Н. Б. Основы имитационного моделирования сложных экономических систем: Учеб. пособие. — М.: Дело, 2003. — 336с.
.Скворцов А.Б. Имитационное моделирование и технология экспертных систем в управлении инфокоммуникационной компанией. — М.: Радио и связь, 2002. — 232 с.
Теги:
Имитационное моделирование бизнес-процессов организации
Курсовая работа (теория)
Менеджмент
- 1
- 2
- 3
- . . .
- последняя »


Функция «чтения» служит для ознакомления с работой. Разметка, таблицы и картинки документа могут отображаться неверно или не в полном объёме!
КУРСОВАЯ РАБОТА
по дисциплине Перспективные информационные системы в экономике
на тему «Имитационное моделирование бизнес-процессов организации»
Содержание Введение
. Цели и задачи имитационного моделирования
2. Выбор, обоснование, схема и описание бизнес-процесса организации
3. Определение состава исходных данных для моделирования
. Статистическое исследование бизнес-процесса
. Идентификация законов распределения случайных величин
6. Разработка и описание моделирующего алгоритма для реализации программы имитационной модели
. Разработка компьютерной программы моделирования бизнес-процесса
8. Технико-экономическая интерпретация полученных результатов
Заключение
Список используемых источников Введение В исследовании операций широко применяются как аналитические, так и статистические модели. Каждый из этих типов имеет свои преимущества и недостатки. Аналитические модели более грубы, учитывают меньшее число факторов, всегда требуют каких-то допущений и упрощений. Зато результаты расчета по ним легче обозримы, отчетливее отражают присущие явлению основные закономерности. А, главное, аналитические модели больше приспособлены для поиска оптимальных решений. Статистические модели, по сравнению, с аналитическими, более точны и подробны, не требуют столь грубых допущений, позволяют учесть большое (в теории — неограниченно большое) число факторов. Но и у них — свои недостатки: громоздкость, плохая обозримость, большой расход машинного времени, а главное, крайняя трудность поиска оптимальных решений, которые приходятся искать «на ощупь», путем догадок и проб.
Наилучшие работы в области исследования операций основаны на совместном применении аналитических и статистических моделей. Аналитическая модель дает возможность в общих чертах разобраться в явлении, наметить как бы контур основных закономерностей. Любые уточнения могут быть получены с помощью статистических моделей.
Имитационное моделирование — метод, позволяющий строить модели , описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику .
Имитационное моделирование применяется к процессам, в ход которых может время от времени вмешиваться человеческая воля. Человек, руководящий операцией, может в зависимости от сложившейся обстановки, принимать те или другие решения, подобно тому, как шахматист, глядя на доску, выбирает свой очередной ход. Затем приводится в действие математическая модель, которая показывает, какое ожидается изменение обстановки в ответ на это решение и к каким последствиям оно приведет спустя некоторое время. Следующее «текущее решение» принимается уже с учетом реальной новой обстановки и т.д. В результате многократного повторения такой процедуры руководитель как бы «набирает опыт», учится на своих и чужих ошибках и постепенно выучивается принимать правильные решения — если не оптимальные, то почти оптимальные.
Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе
- 1
- 2
- 3
- . . .
- последняя »
Интересная статья: Основы написания курсовой работы
< Экономико-математическое моделирование
Поиск на сайте math-solution.ru рефератов, курсовых, дипломных и контрольных работ, презентаций и т.д.
курсовая работа на тему:
Имитационное моделирование бизнес-процессов организации
Обоснование, схема и описание бизнес-процесса организации. Идентификация законов распределения случайных величин. Разработка и описание моделирующего алгоритма для реализации программы имитационной модели. Разработка компьютерной программы моделирования.
Категория: Экономико-математическое моделирование
Предмет: Перспективные информационные системы в экономике
Вид: курсовая работа
< Экономико-математическое моделирование
- Выдержка
- Другие работы
- Помощь в написании
Имитационное моделирование бизнес-процессов организации (реферат, курсовая, диплом, контрольная)
КУРСОВАЯ РАБОТА по дисциплине Перспективные информационные системы в экономике на тему «Имитационное моделирование бизнес-процессов организации»
Содержание Введение
1. Цели и задачи имитационного моделирования
2. Выбор, обоснование, схема и описание бизнес-процесса организации
3. Определение состава исходных данных для моделирования
4. Статистическое исследование бизнес-процесса
5. Идентификация законов распределения случайных величин
6. Разработка и описание моделирующего алгоритма для реализации программы имитационной модели
7. Разработка компьютерной программы моделирования бизнес-процесса
8. Технико-экономическая интерпретация полученных результатов Заключение Список используемых источников
Введение
В исследовании операций широко применяются как аналитические, так и статистические модели. Каждый из этих типов имеет свои преимущества и недостатки. Аналитические модели более грубы, учитывают меньшее число факторов, всегда требуют каких-то допущений и упрощений. Зато результаты расчета по ним легче обозримы, отчетливее отражают присущие явлению основные закономерности. А, главное, аналитические модели больше приспособлены для поиска оптимальных решений. Статистические модели, по сравнению, с аналитическими, более точны и подробны, не требуют столь грубых допущений, позволяют учесть большое (в теории — неограниченно большое) число факторов. Но и у них — свои недостатки: громоздкость, плохая обозримость, большой расход машинного времени, а главное, крайняя трудность поиска оптимальных решений, которые приходятся искать «на ощупь», путем догадок и проб.
Наилучшие работы в области исследования операций основаны на совместном применении аналитических и статистических моделей. Аналитическая модель дает возможность в общих чертах разобраться в явлении, наметить как бы контур основных закономерностей. Любые уточнения могут быть получены с помощью статистических моделей.
Имитационное моделирование — метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику.
Имитационное моделирование применяется к процессам, в ход которых может время от времени вмешиваться человеческая воля. Человек, руководящий операцией, может в зависимости от сложившейся обстановки, принимать те или другие решения, подобно тому, как шахматист, глядя на доску, выбирает свой очередной ход. Затем приводится в действие математическая модель, которая показывает, какое ожидается изменение обстановки в ответ на это решение и к каким последствиям оно приведет спустя некоторое время. Следующее «текущее решение» принимается уже с учетом реальной новой обстановки и т. д. В результате многократного повторения такой процедуры руководитель как бы «набирает опыт», учится на своих и чужих ошибках и постепенно выучивается принимать правильные решения — если не оптимальные, то почти оптимальные.
Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между ее элементами или другими словами — разработке симулятора исследуемой предметной области для проведения различных экспериментов.
Имитационное моделирование позволяет имитировать поведение системы во времени. Причём плюсом является то, что временем в модели можно управлять: замедлять в случае с быстропротекающими процессами и ускорять для моделирования систем с медленной изменчивостью. Можно имитировать поведение тех объектов, реальные эксперименты с которыми дороги, невозможны или опасны. С наступлением эпохи персональных компьютеров производство сложных и уникальных изделий, как правило, сопровождается компьютерным трёхмерным имитационным моделированием. Эта точная и относительно быстрая технология позволяет накопить все необходимые знания, оборудование и полуфабрикаты для будущего изделия до начала производства. Компьютерное 3D моделирование теперь не редкость даже для небольших компании.
Предметом исследования данной работы являются процессы, проходящие в ГБУ «Центр социального обслуживания граждан пожилого возраста и инвалидов городского округа Чапаевск». Более подробно рассматривается бизнес-процесс «Предоставление клиенту социального обслуживания на дому», производится его имитационное моделирование.
1. Цели и задачи имитационного моделирования Свою практическую деятельность ГБУ «Центр социального обслуживания граждан пожилого возраста и инвалидов городского округа Чапаевск» начало с 01.02.1991 г.
Целью деятельности Центра является: осуществление на закрепленной территории организационной, практической и методической деятельности по социальному обслуживанию и оказанию социальных услуг гражданам (семьям), оказавшимся в трудной жизненной ситуации.
Главные принципы в работе: доброжелательность, гуманность, адресность, универсальность, максимизация социальных ресурсов, конфиденциальность и толерантность.
Задачами деятельности Центра являются:
ѕ организация и предоставление гарантированных и дополнительных социальных услуг гражданам пожилого возраста, инвалидам, попавшим в сложную жизненную ситуацию;
ѕ выявление граждан, проживающих на обслуживаемой Учреждением территории и нуждающихся в гарантированных социальных услугах;
ѕ оказание социальных услуг постоянного, временного или разового характера лицам, нуждающимся в социальном обслуживании;
ѕ осуществление трудовой реабилитации клиентов учреждения в цехах, мастерских, и иных структурных подразделения Учреждения, осуществляющих трудотерапию;
ѕ организация срочной социальной помощи;
ѕ содействие лицам с ограничением жизнедеятельности (в том числе инвалидам) в получении медико-социального освидетельствования, реабилитационных мероприятий, технических средств реабилитации и протезно-ортопедических изделий.
Основными функциями Центра являются:
ѕ предоставление социальной поддержки;
ѕ оказание социально-бытовых, социально-медицинских, психолого-педагогических, социально-правовых услуг и оказание материальной помощи;
ѕ проведение социальной адаптации граждан, находящихся в трудной жизненной ситуации.
Центр социального обслуживания предоставляет следующие социальные услуги:
ѕ Отделение социального обслуживания на дому предназначается для временного (до 6 месяцев) или постоянного оказания гражданам, частично утратившим способность к самообслуживанию и нуждающимся в посторонней поддержке, социально — бытовой помощи в надомных условиях. Обслуживание на дому граждан осуществляется путем предоставления им, в зависимости от степени и характера нуждаемости, социально — бытовых, консультативных и иных услуг, входящих в федеральный и территориальный перечни гарантированных государством социальных услуг, оказываемых государственными и муниципальными учреждениями социального обслуживания, а также оказания, по их желанию, дополнительных социальных услуг, не входящих в эти перечни.
ѕ Специализированное отделение социально — медицинского обслуживания на дому предназначается для временного (до 6 месяцев) или постоянного социально — бытового обслуживания и оказания доврачебной медицинской помощи в надомных условиях гражданам, частично или полностью утратившими способность к самообслуживанию и страдающими тяжелыми заболеваниями, в том числе онкологическими в поздних стадиях течения, психическими расстройствами в стадии ремиссии, туберкулезом за исключением активной формы, являющимися противопоказанием к принятию в отделение социального обслуживания на дому.
ѕ Отделение срочного социального обслуживания предназначается для оказания гражданам, остро нуждающимся в социальной поддержке, неотложной помощи разового характера, направленной на поддержание их жизнедеятельности.
ѕ Оказание психологической помощи включает в себя социально-психологическое консультирование, психологическую диагностику и обследование личности, психологическое консультирование, психологическую коррекция, психологическую помощь (в том числе по телефону);
ѕ Оказание юридической помощи включает в себя консультирование по вопросам, связанным с правом граждан на социальное обслуживание в государственной и негосударственной системах социальных служб и защиты своих интересов, оказание помощи в оформлении документов, содействие в осуществлении по отношению к гражданам пожилого возраста инвалидам мер социальной поддержки и получении преимуществ, установленных действующим федеральным и региональным законодательством, содействие в получении юридической помощи, консультаций по социально-правовым вопросам и иных правовых услуг, содействие в получении бесплатной помощи адвоката в порядке, установленном действующим законодательством, оказание других форм срочного социального обслуживания, обусловленных региональными особенностями и предусмотренных территориальным перечнем гарантированных государством социальных услуг.
ѕ Социально-реабилитационное отделение является полустационарным структурным подразделением Центра и предназначается для социально — бытового, культурного, медицинского обслуживания граждан, сохранивших способность к самообслуживанию и активному передвижению, организации их отдыха, привлечения к посильной трудовой деятельности и поддержания активного образа жизни.
В связи с этим, целью имитационного моделирования является анализ состояния и перспектив совершенствования предоставляемых социальных услуг ГБУ «Центр социального обслуживания граждан пожилого возраста и инвалидов городского округа Чапаевск».
Задачами являются:
ѕ анализ делопроизводственной и специальной документации социального учреждения;
ѕ сбор и анализ информации о лицах, обращающихся в Центр и об оказании им социальных услуг;
ѕ сбор и анализ информации о социальном учреждении и обслуживающем персонале;
ѕ определение порядка работы с документами;
ѕ предложения направлений и методов совершенствования социальных услуг.
2. Выбор, обоснование, схема и описание бизнес-процесса организации В рамках курсового проекта выбран один из основных бизнес-процессов организации «Предоставление клиенту социального обслуживания на дому». Выбранный бизнес-процесс позволяет систематизировать работу всех процессов организации, проанализировать работу этих процессов и сделать соответствующие выводы о моделировании и исследовании данного процесса.
Рассмотрим подробно выбранный бизнес-процесс «Предоставление клиенту социального обслуживания на дому» (рис.1).
Бизнес-процесс начинается с обращение потенциального клиента или его законного представителя в учреждение, регистрацию обращения, оформление заявления потенциального клиента на имя руководителя учреждения о рассмотрении возможности предоставления социального обслуживания на дому, которое является основанием для проведения акта обследования материально-бытового положения, ознакомление с нормами и правилами предоставления социального обслуживания на дому, консультирование потенциального клиента, клиента или его законного представителя по вопросам предоставления социального обслуживания на дому.
Учреждение обеспечивает потенциальному клиенту условия для заключения Договора, в соответствии с действующим законодательством, потребностями и особенностями его жизненной ситуации.
Неотъемлемым приложением к Договору является «Перечень согласованных социальных услуг» с указанием наименований социальных услуг, периодичности предоставления, кратности оказания социальных услуг на дому, согласованных с клиентом.
Предоставление социального обслуживания на дому осуществляется только при выполнении клиентом норм и правил предоставления социального обслуживания на дому.
Рис. 1. Бизнес-процесс «Предоставление клиенту социального обслуживания на дому»
3. Определение состава исходных данных для моделирования бизнес процесс моделирование алгоритм Для разработки имитационной модели процесса «Предоставление клиенту социального обслуживания на дому» определим состав исходных данных.
К исходным данным относятся детерминированные и случайные величины, оказывающие основное влияние на рассматриваемый бизнес-процесс.
Исходя из бизнес-процесса, определим состав исходных данных для моделирования. Процесс начинается с поступления от клиента обращения и документов на предоставления социального обслуживания на дому. Время между поступлением обращений носит случайный характер. После получения обращения отдел социального обслуживания на дому начинает проверку документов на соответствие критериям. Время для проведения оценки индивидуальной нуждаемости неодинаково для различных обращений. В том случае, если принято решение о предоставлении социальных услуг, отдел социального обслуживания на дому начинает рассматривать заявление клиента. Время составления заявления о предоставлении социального обслуживания на дому носит случайный характер. Исходя из информации, содержащейся в заявлении от клиента, юридический отдел составляет договор. Приложением к Договору идет Перечень согласованных социальных услуг с клиентом. Время согласования Перечня социальных услуг носит случайный характер. После этого отдел бухгалтерии предъявляет расчетный счет оказанных услуг. Время между подписанием Договора и получением квитанции об оплате социальных услуг клиентом различно.
К детерминированным данным относятся следующие: число каналов, доход от обслуживания одного обращения, издержки обслуживания одного обращения, период работы системы .
К случайным величинам относятся следующие:
ѕ среднее время между соседними обращениями ;
ѕ среднее время проведения оценки индивидуальной нуждаемости ;
ѕ среднее время составления заявления клиентом ;
ѕ среднее время заключения Договора;
ѕ среднее время формирования Перечня социальных услуг ;
ѕ среднее время оплаты социальных услуг .
4. Статистическое исследование бизнес-процесса С целью выявления законов распределения случайных факторов, влияющих на работу подразделения, и оценки параметров законов распределения были проведены статистические наблюдения случайных величин, число которых составило 100.
Исходя из описанного выше бизнес-процесса целесообразно выделить следующие случайные величины, оказывающие влияние на эффективность работы сотрудников Центра социального обслуживания:
ѕ время между поступлением обращений (СВ1);
ѕ продолжительность проведения оценки индивидуальной нуждаемости (СВ2);
ѕ продолжительность составления заявления клиентом (СВ3);
ѕ продолжительность заключения Договора (СВ4);
ѕ продолжительность формирования Перечня социальных услуг (СВ5);
ѕ время между подписанием Договора и получением квитанции об оплате социальных услуг клиентом (СВ6).
Для построения модели необходимо найти законы распределения этих случайных величин. Статистические данные по двум, рассматриваемым в данной работе случайным величинам, приведены в следующем разделе.
5. Идентификация законов распределения случайных величин В рамках курсового проекта проведем идентификацию законов распределения случайных величин выбранного бизнес-процесса «Предоставление клиенту социального обслуживания на дому».
Рассмотрим случайную величину — время между поступлением обращений (СВ1). На основе полученной репрезентативной выборки необходимо сделать предположение о законе распределения исследуемой случайной величины, рассчитать его основные параметры и проверить выдвинутую гипотезу о виде закона распределения.
Проверка статистической гипотезы осуществляется с использованием электронной таблицы Microsoft Excel. Обрабатываемая дискретная выборка случайных чисел преобразуется в интервальный ряд, рассчитываются частоты попадания данной случайной величины в полученные интервалы и определяются числовые характеристики эмпирического распределения.
В табл.1 приведены статистические данные случайной величины времени между поступлением обращений (час).
В качестве первого приближения разбиения имеющейся выборки на интервалы используется так называемая формула Стерджесса:
где — число интервалов;
— число единиц совокупности.
Для нашего случая в соответствии с данной формулой получаем число интервалов, равное 8.
Таблица 1
Рассчитанные значения частот попадания случайной величины в каждый из интервалов; , а также найденные значения дисперсии и выборочной средней представлены в табл.2.
Таблица 2
Частоты, выборочные средние и дисперсия случайной величины времени между поступлением обращений
|
№ |
Частота |
Частость, |
Центральный интервал, |
Среднее выборочное, |
Отклонение от среднего, |
Квадрат отклонения, |
Дисперсия, |
|||
|
14,25 |
0,28 |
10,63 |
297,5 |
— 15,73 |
247,51 |
6930,32 |
||||
|
14,25 |
21,5 |
0,21 |
17,88 |
375,38 |
— 8,48 |
71,95 |
1511,01 |
|||
|
21,5 |
28,75 |
0,15 |
25,13 |
376,88 |
— 1,23 |
1,52 |
22,79 |
|||
|
28,75 |
0,11 |
32,38 |
356,13 |
6,02 |
36,21 |
398,31 |
||||
|
43,25 |
0,08 |
39,63 |
317,0 |
13,27 |
176,03 |
1408,21 |
||||
|
43,25 |
50,5 |
0,06 |
46,88 |
281,25 |
20,52 |
420,97 |
2525,81 |
|||
|
50,5 |
57,75 |
0,06 |
54,13 |
324,75 |
27,77 |
771,03 |
4626,2 |
|||
|
57,75 |
0,05 |
61,38 |
306,88 |
35,02 |
1226,23 |
6131,13 |
||||
|
Итого |
2635,75 |
235,54 |
||||||||
Выборочная средняя .
Дисперсия .
СКО =15,354.
Параметр .
Полученное распределение наглядно иллюстрирует гистограмма частости интервального ряда, показанная на рис. 2.
Рис. 2. Гистограмма распределения частости случайной величины, времени между поступлением обращений Вид гистограммы на рис. 2 позволяет предположить, что исследуемая случайная величина подчиняется экспоненциальному закону распределения с параметром .
Для проверки данной гипотезы воспользуемся критерием согласия (критерий Пирсона). При этом необходимо оценить значение суммы вида
где — частота эмпирического распределения в интервале ;
— частоты теоретического распределения в интервале ;
— число наблюдений;
— теоретическая вероятность попаданий значений случайной величины в заданный интервал;
— число интервалов наблюдения.
Значения эмпирической вероятности определяются отношением частоты попадания значений случайной величины в заданный интервал к общему числу наблюдений.
Чем меньше различаются между собой значения теоретической и эмпирической вероятностей, тем меньше значение критерия .
Вычисленные теоретические вероятности попадания значений исследуемой случайной величины в заданные интервалы приведены в табл.2; а соответствующие данным таблиц 2 и 3 значения критерия — в табл.4.
Таблица 3
Теоретические вероятности для случайной величины
|
№ |
||||||||
|
14,25 |
— 0,27 |
— 0,54 |
0,7668 |
0,5824 |
0,1844 |
|||
|
14,25 |
21,5 |
— 0,54 |
— 0,82 |
0,5824 |
0,4423 |
0,14 |
||
|
21,5 |
28,75 |
— 0,82 |
— 1,09 |
0,4423 |
0,3360 |
0,1064 |
||
|
28,75 |
— 1,09 |
— 1,37 |
0,3360 |
0,2552 |
0,0808 |
|||
|
43,25 |
— 1,37 |
— 1,64 |
0,2552 |
0,1938 |
0,0614 |
|||
|
43,25 |
50,5 |
— 1,64 |
— 1,92 |
0,1938 |
0,1472 |
0,0466 |
||
|
50,5 |
57,75 |
— 1,92 |
— 2,19 |
0,1472 |
0,1118 |
0,0354 |
||
|
57,75 |
— 2,19 |
— 2,47 |
0,1118 |
0,0849 |
0,0269 |
|||
Сумма значений .
Приведенное в табл.4 значение необходимо сравнить с критическим значением. Найденным по таблицам распределения Стьюдента.
Таблица 4
Результаты расчета значений
|
№ |
||||||
|
0,1844 |
18,4388 |
9,56 |
91,42 |
|||
|
0,14 |
14,0047 |
7,0 |
48,93 |
|||
|
0,1064 |
10,6369 |
4,36 |
19,04 |
|||
|
0,0808 |
8,0790 |
2,92 |
8,53 |
|||
|
0,0614 |
6,1362 |
1,86 |
3,47 |
|||
|
0,0466 |
4,6606 |
1,34 |
1,79 |
|||
|
0,0354 |
3,5398 |
2,46 |
6,05 |
|||
|
0,0269 |
2,6886 |
2,31 |
5,34 |
|||
Значение параметра .
Выбрав уровень значимости и учитывая, что в данном случае число степеней свободы, находим значение. Поскольку, был сделан вывод о том, что его значение попадает в область принятия данной статистической гипотезы. Следовательно, полученные данные о законе распределения рассматриваемой случайной величины (времени между поступлением обращений) не противоречат предположению о ее экспоненциальном распределении с параметром .
Проведем идентификацию законов распределения для следующей случайной величины — продолжительность проведения оценки индивидуальной нуждаемости (СВ2).
Значения случайной величины приведены в табл. 5 (час).
Таблица 5
Таблица 6
Частоты, выборочные средние и дисперсия
|
№ |
Частота |
Частость, |
Центральный интервал, |
Среднее выборочное, |
Отклонение от среднего, |
Квадрат отклонения, |
Дисперсия, |
|||
|
1,0 |
12,3 |
0,55 |
6,63 |
364,38 |
— 12,26 |
150,37 |
8270,29 |
|||
|
12,3 |
23,5 |
0,16 |
17,88 |
286,0 |
— 1,01 |
1,03 |
16,4 |
|||
|
23,5 |
34,8 |
0,13 |
29,13 |
378,63 |
10,24 |
104,81 |
1362,48 |
|||
|
34,8 |
0,06 |
40,38 |
242,25 |
21,49 |
461,71 |
2770,28 |
||||
|
57,3 |
0,05 |
51,63 |
258,13 |
32,74 |
1071,74 |
5358,72 |
||||
|
57,3 |
68,5 |
0,02 |
62,88 |
125,75 |
43,99 |
1934,9 |
3869,8 |
|||
|
68,5 |
79,8 |
0,02 |
74,13 |
148,25 |
55,24 |
3051,18 |
6102,36 |
|||
|
79,8 |
91,0 |
0,01 |
85,38 |
85,38 |
66,49 |
4420,59 |
4420,59 |
|||
|
Итого |
1888,75 |
321,71 |
||||||||
Выборочная средняя .
Дисперсия .
СКО =17,94.
Параметр .
Рис. 3. Гистограмма распределения частости случайной величины
Таблица 7
Теоретические вероятности для случайной величины
|
№ |
||||||||
|
1,0 |
12,3 |
— 0,05 |
— 0,65 |
0,9484 |
0,5228 |
0,4256 |
||
|
12,3 |
23,5 |
— 0,65 |
— 1,24 |
0,5228 |
0,2882 |
0,2346 |
||
|
23,5 |
34,8 |
— 1,24 |
— 1,84 |
0,2882 |
0,1588 |
0,1293 |
||
|
34,8 |
— 1,84 |
— 2,44 |
0,1588 |
0,0876 |
0,0713 |
|||
|
57,3 |
— 2,44 |
— 3,03 |
0,0876 |
0,0483 |
0,0393 |
|||
|
57,3 |
68,5 |
— 3,03 |
— 3,63 |
0,0483 |
0,0266 |
0,0217 |
||
|
68,5 |
79,8 |
— 3,63 |
— 4,22 |
0,0266 |
0,0147 |
0,0119 |
||
|
79,8 |
91,0 |
— 4,22 |
— 4,82 |
0,0147 |
0,0081 |
0,0066 |
||
Сумма значений .
Таблица 8
Результаты расчета значений
|
№ |
||||||
|
0,4256 |
42,5643 |
12,44 |
3,63 |
|||
|
0,2346 |
23,4620 |
— 7,46 |
2,37 |
|||
|
0,1293 |
12,9326 |
0,07 |
0,00 |
|||
|
0,0713 |
7,1286 |
— 1,13 |
0,18 |
|||
|
0,0393 |
3,9294 |
1,07 |
0,29 |
|||
|
0,0217 |
2,1659 |
— 0,17 |
0,01 |
|||
|
0,0119 |
1,1939 |
0,81 |
0,54 |
|||
|
0,0066 |
0,6581 |
0,34 |
0,18 |
|||
Значение параметра .
Приведенное в табл.8 значение необходимо сравнить с критическим значением. Найденным по таблицам распределения Стьюдента. Выбрав уровень значимости и учитывая, что в данном случае число степеней свободы, находим значение. Поскольку, был сделан вывод о том, что его значение попадает в область принятия данной статистической гипотезы. Следовательно, полученные данные о законе распределения рассматриваемой случайной величины не противоречат предположению о ее экспоненциальном распределении с параметром.
Аналогично была проведена идентификация законов распределения для других случайных величин, в ходе которой получены следующие результаты:
ѕ продолжительность составления заявления клиентом (СВ3) — экспоненциальный закон распределения с параметром ;
ѕ продолжительность заключения Договора (СВ4) — экспоненциальный закон распределения с параметром ;
ѕ продолжительность формирования Перечня социальных услуг (СВ5) — экспоненциальный закон распределения с параметром ;
ѕ время между подписанием Договора и получением квитанции об оплате социальных услуг клиентом (СВ6) — экспоненциальный закон распределения с параметром .
6. Разработка и описание моделирующего алгоритма для реализации программы имитационной модели Для проектирования модели используются данные о деятельности Центра социального обслуживания граждан пожилого возраста и инвалидов городского округа Чапаевск, а также информация об изменениях этих данных и максимально подробное описание всех операций, осуществляемых с ними сотрудниками организации. Недостаток такого рода сведений может привлечь за собой необходимость пересмотра самого способа построения модели.
Для описания работы Центра подходит математическая схема СМО. Для таких клиентов характерны три отличительные особенности:
ѕ имеется поток клиентов, желающих быть обслуженными;
ѕ имеются каналы обслуживания, которые обеспечивают удовлетворение обращений клиентов (в данном случае сотрудники Центра);
ѕ имеется определенный набор правил обслуживания клиентов.
Поскольку неизвестно, сколько целесообразно всего иметь сотрудников в Центре для обработки обращений, то число каналов обслуживания в модели должно быть переменным. Оно будет зависеть от соотношения между средним временем между поступлениями обращений и средним временем рассмотрения этих обращений, — поэтому необходимо учитывать эти случайные величины.
Следует помнить, что реальные процессы, протекающие в организации, все же слишком сложны, чтобы полностью и исчерпывающе их понять и описать. Возникшие проблемные ситуации связаны с практическим бесконечным числом элементов, переменных, параметров, ограничений и т. д., поэтому при моделировании необходимо поступить разумно и отбросить достаточно большую часть их характеристик, выделив лишь те особенности, которые позволяют воссоздать идеализированный вариант каждой проблемной ситуации. Следовательно, модель работы организации дает всегда упрощенное представление о фрагменте реального бизнеса; от того, насколько корректно сконструировано это представление, зависит степень адекватности модели и действительности.
Для имитационной модели вполне достаточно изложения общих принципов с указанием условных характеристик объекта исследования.
Так же необходимо знать, как будут вести себя клиенты, если им придется стоять в очереди.
При описании нашей СМО наиболее подходящим является режим ожидания «с неограниченным ожиданием».
Правило обслуживания состоит в том, что очередное обращение поступает в тот канал, который раньше других освободился. Так как в нашем случае режим неограниченного ожидания, то обращение может покинуть систему необслуженной в том случае, если время ожидания начала обслуживания превышает величину Ткон (период функционирования СМО).
Входными характеристиками модели являются:
ѕ число каналов ;
ѕ среднее время между соседними обращениями ;
ѕ среднее время проведения оценки индивидуальной нуждаемости ;
ѕ период работы системы ;
ѕ число случайных реализаций процесса ;
ѕ среднее время составления заявления клиентом ;
ѕ среднее время заключения Договора;
ѕ среднее время формирования Перечня социальных услуг ;
ѕ среднее время оплаты социальных услуг .
Выходной характеристикой модели является среднее число обслуженных обращений
В качестве показателя эффективности работы системы выберем среднюю прибыль:
где — чистая прибыль, полученная в результате обслуживания одного обращения;
— издержки обслуживания всех обращений, зависящих от числа каналов.
Если разделить обе части равенства на, получим формулу для нахождения показателя эффективности:
где — средняя относительная прибыль,
— функция числа каналов.
Основным вариантом функциональной зависимости является возрастающая зависимость с положительной второй производной. Отсюда следует:
.
Для расчета показателя эффективности будем использовать формулу:
.
В качестве критерия выбора неивыгоднейшей структуры СМО принимается оптимальное число каналов обслуживания, обеспечивающее максимум средней относительной прибыли:
где — наивыгоднейшее число каналов.
Количество клиентов за один рабочий день будет определяться в зависимости от времени прихода клиентов и времени обслуживания этих клиентов, но эта величина не может превышать максимальное количество клиентов. Клиент обслуживается в том случае, если он появился до окончания рабочего времени, и если время его обслуживания не будет превышать рамки рабочего времени.
В результате моделирования будет получено оптимальное количество сотрудников Центра, то есть такое, при котором прибыль данного отдела, следовательно, и организации в целом, станет максимальной при наименьших затратах на содержание данного отдела.
Представим моделирующий алгоритм в графической форме (рис.4). Графической формой представления моделирующих алгоритмов являются структурные схемы.
Рис. 4. Обобщенная схема моделирующего алгоритма Рассмотрим каждый из блоков моделирующего алгоритма в отдельности. В блоке 1 осуществляется ввод исходных данных. Блок 1а служит для проверки данных на соответствие какому-либо закону распределения. В блоке 2 осуществляется установка начальных значений параметров модели, то есть обнуление счетчиков и переменных. В блоке 3 производится моделирование системы, в которой возможны очереди клиентов, но нет отказа технических подсистем. В блоке 4 производится расчет критерия эффективности — средней относительной прибыли, являющейся основным результатом моделирования системы. Блок 5 позволяет по полученным результатам моделирования построить диаграммы распределения процесса предоставления социальных услуг в зависимости от числа сотрудников Центра, обслуживающих обращения.
Рассмотрим более подробно блок 3, в котором производится непосредственное моделирование системы. Обобщенная блок-схема представлена на рис. 5.
Моделирование начинается с обнуления значений времени поступления обращений — блок 1. Во 2 блоке счетчику цикла i присваивается значение 1. В блоке 3 проверяется условие. В данном случае цикл состоит из 100 итераций. Если условие блока 3 выполняется, в 4 блоке происходит моделирование по показательному закону случайной величины времени поступления обращений и увеличение значения данной переменной. В блоке 5 счетчик цикла увеличивается на 1, и осуществляется переход к блоку 3. Если условие блока 3 не выполняется, цикл завершается и в блоке 6 определяется среднее значение данной переменной. На этом заканчивается моделирование времени поступления клиентов, и начинается моделирование времени проведения оценки индивидуальной нуждаемости.
В блоке 7 происходит обнуление значений времени проведения оценки индивидуальной нуждаемости. Далее аналогично предыдущей переменной осуществляется моделирование среднего значения данной переменной, т.к. закон распределения такой же, как и в предыдущем случае. Значение параметра закона распределения берется из соответствующей ячейки параметров законов распределения. Моделирование проведения оценки индивидуальной нуждаемости в блоках 7−12. Далее моделирование времени составления заявления клиентом — блоки 13−18. Затем моделирование времени заключения Договора — блоки 19−24, времени формирования Перечня социальных услуг — блоки 25−30, времени оплаты социальных услуг — блоки 31−36. В блоке 37 проверяется окончание времени моделирования. Если условие блока выполняется, то происходит переход к блоку 3 и моделирование продолжается, если же нет, то полученные результаты фиксируются и моделирование завершается.
Рис. 5. Обобщенная блок-схема алгоритма блока 3 «Моделирование системы»
7. Разработка компьютерной программы моделирования бизнес-процесса Имитационная модель, рассматриваемая в рамках курсового проекта, написана на языке программирования Delphi 7.
Delphi — одна из самых мощных систем, позволяющих на самом современном уровне создавать как отдельные прикладные программы Windows, так и разветвленные комплексы, предназначенные для работы в корпоративных сетях и в Интернет. Это продукт, уникальным образом сочетающий высокопроизводительный компилятор, объектно-ориентированные средства визуального программирования и универсальный механизм доступа к базам данных.
Delphi — это система визуального объектно-ориентированного программирования, позволяющая решать множество задач, в частности:
1. Создавать законченные приложения для Windows самой различной направленности, от чисто вычислительных и логических, до графических и мультимедиа.
2. Быстро создавать профессионально выглядящий оконный интерфейс для любых приложений, написанных на любом языке; интерфейс удовлетворяет всем требованиям Windows и автоматически настраивается на ту систему, которая установлена на компьютере пользователя, поскольку использует многие функции, процедуры, библиотеки Windows.
3. Создавать мощные системы работы с локальными и удаленными базами данных любых типов; при этом имеются средства автономной отладки приложения с последующим выходом в сеть.
4. Создавать многозвенные распределенные приложения, основанные на различных технологиях.
5. Создавать приложения различных классов для работы в Интернет.
6. И многое другое, включая создания отчетов, справочных систем, библиотек DLL, компонентов ActiveX.
Рассмотрим подробно процесс работы системы.
Работа пользователя с программой начинается с экранной формой «Ввод исходных данных» (рис. 6). В данной форме необходимо ввести исходные данные и задать необходимые параметры моделирования.
Рис. 6. Форма «Ввод исходных данных»
Исходные данные вводятся в специальные поля. Нажатие на кнопки «Введите исходные данные» и «Параметры законов распределения» обнуляет значения специальных полей.
После ввода исходных данных с помощью кнопки «Моделировать» осуществляется непосредственное моделирование и получение выходных данных и открывается новая форма «Результаты моделирования» (рис. 7).
Рис. 7. Форма «Результаты моделирования»
Из данной формы можно перейти в форму «Вывод результатов», нажав на кнопку «Рассчитать среднюю относительную прибыль» (рис. 8).
Возврат к форме «Ввод исходных данных» осуществляется с помощью нажатия на кнопку «Исходные данные».
Рис. 8. Форма «Вывод результатов»
В результате работы имитационной модели получили следующие результаты — наибольшее значение средней относительной прибыли достигается, если обслуживанием обращений занимается 4 сотрудника Центра социального обслуживания.
8. Технико-экономическая интерпретация полученных результатов Программа, написанная в среде Borland Delphi 7, для моделирования бизнес-процесса «Предоставление клиенту социального обслуживания на дому» позволяет прослеживать интерпретацию полученного результата.
В основе интерпретации лежит процедура объяснения полученных результатов на основе принятой в исследовании концепции.
В задачи интерпретации входят: выявление объективного значения полученных результатов для оптимизации работы организации, а также смысла, т. е. значения для самого исследователя или заинтересованного в результатах исследования круга лиц.
В результате нескольких прогонов модели было выявлено, что с учетом всех исходных данных: максимальное количество клиентов, среднее время между поступлением обращений, среднее время обслуживания клиентов, продолжительность рабочего дня — был получен результат, который наглядно демонстрирует, каким должно быть оптимальное количество сотрудников Центра социального обслуживания, при котором прибыль отдела социального обслуживания на дому, следовательно, и организации в целом, станет максимальной при наименьших затратах на содержание данного отдела. И в результате проведенных исследований было выявлено, что оптимальное количество специалистов, работающих с клиентами должно быть равным 4.
Работу данной модели можно использовать для прогнозирования работы управления в будущем и на основании полученных приблизительных результатов делать выводы о результатах работы и принимать необходимые меры по улучшению показателей работы организации.
Заключение
В рамках данного курсового проекта разработана имитационная модель для применения в ГБУ «Центр социального обслуживания граждан пожилого возраста и инвалидов городского округа Чапаевск». Имитационная модель предназначена для моделирования бизнес-процесса «Предоставление клиенту социального обслуживания на дому».
При разработке имитационной модели были определены и обоснованы параметры имитационной модели, идентифицированы законы распределения случайных величин, разработан моделирующий алгоритм.
В результате выполнения данного курсового проекта были получены практические знания в области имитационного моделирования экономических процессов.
Был решен следующий круг задач: структуризация конкретного бизнес-процесса с позиции решения задач принятия управленческих решений в рамках современной экономической информационной системы; применение технологии компьютерного моделирования для решения конкретной задачи повышения эффективности управления бизнес-процессом.
Имитационное моделирование является одним из самых мощных, перспективных и эффективных инструментов моделирования бизнес-процессов, особенно в ситуациях, когда необходимо принимать обоснованные и целенаправленные решения в условиях неопределенности. Этот подход базируется на возможность моделирования проблемных ситуаций организаций в условиях экономической нестабильности и рисков. При этом руководству организации предлагается следовать принципу комплексного применения рационального и интуитивного анализа возникающих проблем, их раннему диагностированию и предупреждению.
Список используемых источников
1. Гмурман В. Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. Изд.7-е, стер. — М.: Высшая школа, 2010. — 479 с.
2. Димов Э. М., Богданова Е. А. Методическое пособие к курсовой работе на тему «Имитационное моделирование бизнес-процессов компании» для студентов специальности 80 801 (Прикладная информатика в экономике). — Самара: ПГАТИ, 2007. — 31 с.
3. Димов Э. М., Маслов О. Н., Скворцов А. Б. Новые информационные технологии: Подготовка кадров и обучение персонала. Часть 1. Реинжиниринг и управление бизнес-процессами в инфокоммуникациях. Научное издание. — М.: ИРИАС, 2009. — 386 с.
4. Кобелев Н. Б. Основы имитационного моделирования сложных экономических систем: Учеб. пособие. — М.: Дело, 2003. — 336с.
5. Скворцов А. Б. Имитационное моделирование и технология экспертных систем в управлении инфокоммуникационной компанией. — М.: Радио и связь, 2002. — 232 с.
Показать весь текст
Заполнить форму текущей работой