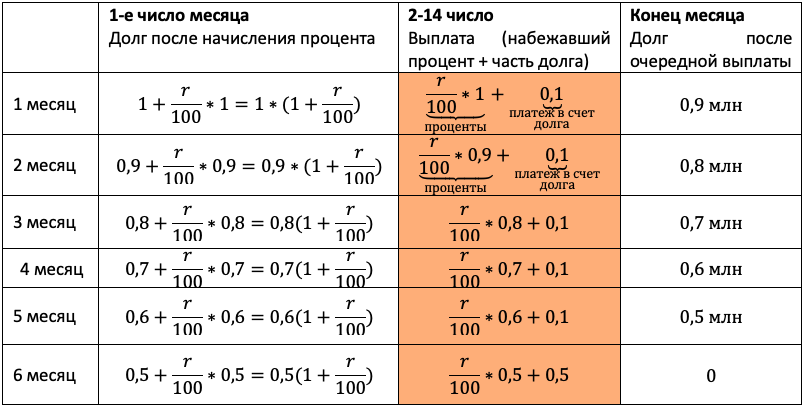
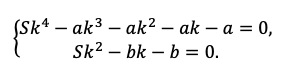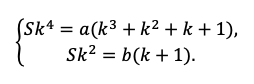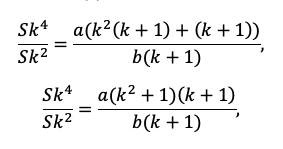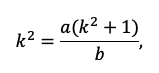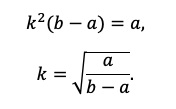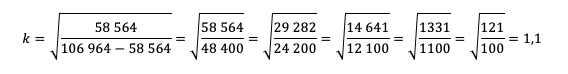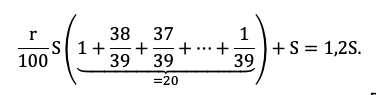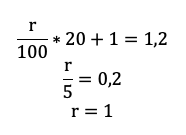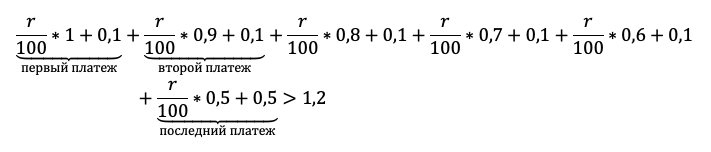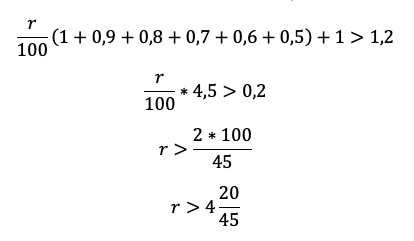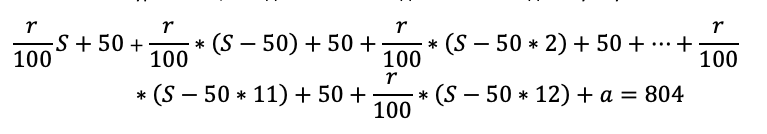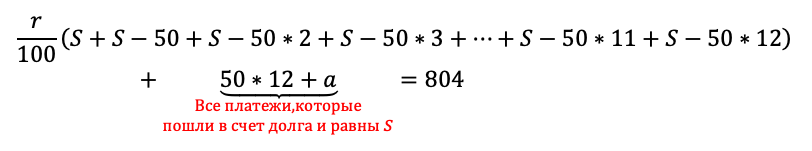|
Единственный в мире Музей Смайликов |
|


Подборка по базе: Текстовые задачи 10-11 кл..pdf, функции и задачи таможенных органов.pptx, алгоритм решения задачи.odt, ФОС задачи (1).docx, Ситуационные задачиNew.pdf, Лекция Цифровые инструменты.pdf, Решение задачи.odt, Практические (ситуационные ) задачи.doc, Ситуационные задачи с решением по уголовному процессуальному пра, 30. Задачи на построение.docx
Задача 22
Компания получила кредит на три года в размере 234000 руб. с условием возврата 456000 руб. Определить процентную ставку для случаев простого и сложного процента.
Решение. Для простого процента имеем соотношение 456000 = 234000∙(1 + 3i). Откуда ; или 32,75%.
Для сложного процента ;
или 24,91%.
Задача 23
Вклад открыт под 14% простых годовых. На него начислен процентный платеж в сумме 1500 руб. Найдите величину вклада, если он был открыт на: а) 10 лет, б) 1 год, в) 6 месяцев, г) 10 дней. Временная база K = 365 дней.
Решение. Воспользуемся формулой для вычисления процентного платежа .
а) ; ;
Решение задачи 23. Задача 24
б) 1500 = ; ;
в) ; .
Задача 24. Вексель стоимостью 100000 руб. учитывается за 4 года до погашения по сложной учетной ставке 15% годовых. Найдите сумму, получаемую векселедержателем, и величину дисконта.
Решение. Искомая сумма равна
.
Задача 25.
Клиент имеет вексель на 16000 у.е., который он хочет учесть 10.01.2009 г. в банке по сложной учетной ставке 8%. Какую сумму он получит, если срок до погашения 10.07.2009 г.?
Решение. Найдём время t до погашения векселя. 10,01 – день №10; 10,07 – день №191; число дней равно 191 – 10 = 181; . Сумма, полученная векселедержателем равна .
Задача 26
Предприятие получило кредит на один год в размере 7 млн. руб. с условием возврата 7,77 млн. руб. Рассчитайте процентную и учетную ставку.
Решение. Процентная ставка вычисляется по формуле . Откуда ;
; или 11%.
Учётная ставка вычисляется по формуле
. Откуда 7000000 = 7770000 ;
Решение задачи 26. Задача 27
; или 9,9%.
Задача 27. Банк учитывает вексель по номинальной учетной ставке 10% с ежемесячным начислением процентов. Найти сложную учетную ставку, при которой доход банка не изменился.
Решение. Искомая учётная ставка является эффективной учётной ставкой и вычисляется по формуле .
или 9,55%.
Задача 28. Задача 29
Задача 28. Вексель стоимостью 550 тыс. руб. учитывается за три года до погашения по сложной учетной ставке 12% годовых. Найти сумму, которую получит векселедержатель, и величину дисконта.
Решение. Искомая сумма равна
.
Задача 29. Клиент имеет вексель на 20000 руб., который он хочет учесть 24.04.2011 г. в банке по сложной учетной ставке 10%.
Задачи 29, 30
Какую сумму он получит, если срок погашения 12.09.2011 г.?
Решение. Найдём время t с момента учёта до момента погашения векселя. 24.04 – день №114; 12.09 –день № 255; число дней 255 – 114 = 141; . Сумма, полученная клиентом равна
Задача 30. Номинальная учетная ставка равна 10%. При этом проценты начисляются ежеквартально. Найти эффективную учетную ставку.
Решение задачи 30. Задача31
Эффективная учётная ставка равна или 9,63%.
Задача 31. Что выгоднее, положить 1000 у.е. в банк на год под 8% годовых или купить за 1000 у.е. вексель с номиналом 1100 у.е. и погашением через год? Чему равна доходность покупки векселя, измеренная в виде годовой ставки процентов?
Решение задачи 31. Задача 32
Наращенная сумма при вкладе в банк равна . Покупка векселя с номиналом 1100 выгоднее. Доходность покупки векселя вычисляется по формуле ; 1100 = 1000∙(1 +i); 1 + i = 1,1; i =0,1 или 10%.
Задача 32. Вексель куплен за 200 дней до его погашения. На момент покупки рыночная простая учетная ставка составляла 7% годовых.
Задача 32
Через 5 дней вексель продали по учетной ставке 6% годовых. Оцените эффективность данной финансовой операции в виде ставки простых процентов. Временная база K = 365 дней.
Решение. Вексель куплен за сумму
. Вексель продан за сумму . Эффективность операции выражается по формуле . Откуда
; ; или 47,83% .
Задачи 33, 34
Задача 33. Найти сложную процентную ставку , эквивалентную непрерывной ставке 8%. Ответ привести с точностью до 0,01%.
Решение. Искомая ставка процентов равна или 8,33%.
Задача 34. Найти сложную процентную ставку , эквивалентную простой ставке 10%.
Решение. Используя формулу эквивалентности сложной и простой
Основы финансовой математики
Примеры решений задач по финансовой математике
В этом разделе вы найдете примеры Решенных задач по финансовой математике (финансовым вычислениям) на основные темы, решаемые студентами: начисление процентов (простой, сложный, непрерывный), учетная ставка, инфляция, ренты и потоки платежей, эквивалентные процентные ставки, денежный поток и т. п.
Если вам нужна помощь с подобными заданиями, обращайтесь. Выполним ответственно, недорого, подробно, от 100 рублей за задачу, сроки от 1 дня, гарантия месяц.
Основы финансовых вычислений онлайн
Задача 1. Вексель на сумму 10 000 рублей с погашением 30 ноября предъявлен в банк для оплаты 20 сентября по учётной ставке 20% годовых. Определить сумму, выплаченную владельцу векселя и сумму дисконта при германской практике расчётов.
Задача 2. На сколько изменится срок удвоения вклада, если от простых процентов i = 18% перейти к начислению сложных процентов?
Задача 3. Определить современную стоимость годовой ренты при начислении процентов ежеквартально, если номинальная ставка 18%, размер отдельного платежа 10 000 рублей, длительность ренты 3 года.
Примеры решений: проценты и начисления
Задача 5. Вклад в размере 300 р. помещен в банк 6 февраля и востребован 20 декабря. Ставка 80% годовых. Определить сумму начисленных процентов при различных методах определения срока начисления.
Задача 9. Компания получила кредит на три года в размере 234000 руб. с условием возврата 456000 руб. Определить процентную ставку для случаев простого и сложного процента.
Задача 10. Номинальная учетная ставка равна 10%. При этом проценты начисляются ежеквартально. Найти эффективную учетную ставку.
Задача 11. 1. Темп инфляции $alpha$ за период $t = t_1 + t_2$ равен 0,37. Темп инфляции за второй период на 55% выше, чем за первый. Найти темп инфляции за каждый период.
2. Найти сложную процентную ставку, эквивалентную непрерывной ставке 8% $i_c$.
Задача 12. На счет в банке помещено 160000 рублей. За первые 5 лет и 6 месяцев процентная ставка равнялась 10%, а в следующие 7 лет и 4 месяца – 8%, капитализация полугодовая. Чему будет равна наращенная величина вклада через 12 лет 10 месяцев.
Примеры решений: кредиты, ссуды, ренты
Задача 4. Рассчитать размер ежегодной выплаты для погашения ссуды размером 220000 р., взятую на 7 лет под 9% годовых, а также основные платежи, плату по процентам и остаток долга после очередной выплаты.
Задача 6. Оцените ренту пренумерандо с ежегодными платежами в конце каждого года в сумме 150 тыс. руб., сложные проценты по учетной ставке 15% годовых, срок ренты — 10 лет. Сравните полученные результаты с оценкой ренты, на платежи которой начисляются сложные ссудные проценты по ставке 15% годовых.
Задача 8. Ссуда 150000 руб. выдана на 4 года под 20% годовых (простые проценты). Во сколько раз увеличится наращенная сумма?
Примеры решений: финансовый поток
Задача 7. Вы имеете на счете 40 000 долл. и прогнозируете свой доход в течение следующих 2 лет в сумме 60 000 долл. и 70 000 долл. соответственно. Ожидаемая процентная ставка в эти годы будет 8 и 14%. Ваши минимальные расходы составят: в текущем году — 20 000 долл.; в следующие годы ожидается их прирост с темпом 10% в год. Рассчитайте потенциально доступную сумму к потреблению в каждом из следующих 2-х лет.
Задача 13. Приведите поток $CF = <(0, 600), (1, 250), (2, 350), (3, 600)>$ к моменту времени $t = 2$ при ставке 8%.
Задача 14. Дайте определение внутренней нормы доходности потока и найдите ее для потока $СF= <(0, –2500), (1,2000), (2, 3500)>$.
Определить сумму начисленных процентов при различных методах определения срока начисления.
Www. matburo. ru
22.11.2018 21:57:44
2018-11-22 21:57:44
Источники:
Https://www. matburo. ru/ex_emm. php? p1=emmfm
Основы стохастической финансовой математики. В двух томах. Том 1. Факты. Модели. Том 2. Теория | Ширяев А. Н. | Магазин «Математическая книга» » /> » /> .keyword { color: red; } Основы финансовой математики
Основы стохастической финансовой математики. В двух томах. Том 1. Факты. Модели. Том 2. Теория
Основы стохастической финансовой математики. В двух томах. Том 1. Факты. Модели. Том 2. Теория
Настоящая книга призвана дать весьма широкое представление о предмете финансовой математики, ее истории, основных этапах становления ее теорий, теории арбитража и расчетов в стохастических финансовых моделях.
В книге уделяется значительное внимание не только моделям с дискретным временем, но и моделям в непрерывном времени, включая нужные в финансовой математике темы: теорема Гирсанова, преобразование Эшера, формулы Башелье и Блэка––Шоулса для расчетов опционов европейского типа и др.
Настоящая книга призвана дать весьма широкое представление о предмете финансовой математики, ее истории, основных этапах становления ее теорий, теории арбитража и расчетов в стохастических финансовых моделях.
Biblio. mccme. ru
06.04.2017 0:15:37
2017-04-06 00:15:37
Источники:
Https://biblio. mccme. ru/node/5515/shop
Основы стохастической финансовой математики. Том 1. Факты. Модели (комплект из 2 книг) (А. Н. Ширяев) — купить книгу с доставкой в интернет-магазине «Читай-город». ISBN: 978-5-4439-0395-8 » /> » /> .keyword { color: red; } Основы финансовой математики
Основы стохастической финансовой математики. Том 1. Факты. Модели (комплект из 2 книг)
Основы стохастической финансовой математики. Том 1. Факты. Модели (комплект из 2 книг)
Настоящая книга призвана дать весьма широкое представление о предмете финансовой математики, ее истории, основных этапах становления ее теорий, теории арбитража и расчетов в стохастических финансовых моделях. В книге уделяется значительное внимание не только моделям с дискретным временем, но и моделям в непрерывном времени, включая нужные в финансовой математике темы: теорема Гирсанова, преобразование Эшера, формулы Башелье и Блэка–Шоулса для расчетов опционов европейского типа и др.
Новинки раздела
Издание предназначено для подготовки учащихся 11-х классов к ЕГЭ по биологии. Теория по предмету приведена в полном объеме и соответствует кодификатору элементов содержания и требований к уровню подготовки выпускников общеобразовательных учреждений для. Издание предназначено для подготовки учащихся 11-х классов к ЕГЭ по биологии. Теория по предмету приведена в полном объеме и соответствует кодификатору элементов содержания и требований к уровню подготовки выпускников общеобразовательных учреждений для проведения единого государственного экзамена. Материал изложен в той последовательности, в которой он будет представлен на реальном экзамене, соответствует темам, проверяемым на ЕГЭ, и четко распределен по заданиям (от 1 до 28). Перед каждым теоретическим блоком приводится разбор экзаменационных заданий с подробными рекомендациями по решению. Для проверки знаний в конце книги дано 5 тренировочных вариантов с ответами. Издание может быть использовано учащимися для подготовки к экзамену, учителями и репетиторами для организации учебного процесса и выявления реального уровня подготовки выпускников. Скрыть Показать весь текст
В сборник вошли основополагающие труды всемирно известного философа, психолога и психиатра Рэймонда Моуди: «Жизнь после жизни» — первое исследование так называемого околосмертного опыта, или околосмертных переживаний. Автор проанализировал более ста отчетов. В сборник вошли основополагающие труды всемирно известного философа, психолога и психиатра Рэймонда Моуди:
«Жизнь после жизни» — первое исследование так называемого околосмертного опыта, или околосмертных переживаний. Автор проанализировал более ста отчетов пациентов, переживших клиническую смерть, и выделил общие мотивы, повторяющиеся в их рассказах. Этот мировой бестселлер, впервые опубликованный в 1975 году, произвел настоящую революцию в мировом сознании, радикально изменив отношение общества, в том числе врачей и ученых, к смерти и умиранию.
«Свет вдали» — продолжение многолетних исследований жизни после жизни: ответы на вопросы читателей, наблюдения медицинских работников, задокументированные случаи околосмертного опыта и, конечно, новые научные изыскания. Как последние открытия в медицине, психиатрии и социологии приближают нас к разгадке тайны жизни и смерти?
«Жизнь после утраты» — всеобъемлющее руководство, адресованное тем, кто столкнулся со смертью родных и близких людей. Скрыть Показать весь текст
Все любят мемы. Если вы не скроллите ленту новостей в соцсетях в поиске свежих мемов, то точно получаете их от друзей и родственников в мессенджерах или узнаете о них от коллег. Вы думаете, что мемы появились недавно, с внедрением в нашу жизнь. Все любят мемы. Если вы не скроллите ленту новостей в соцсетях в поиске свежих мемов, то точно получаете их от друзей и родственников в мессенджерах или узнаете о них от коллег. Вы думаете, что мемы появились недавно, с внедрением в нашу жизнь интернет-технологий? А что вы скажете, если узнаете, что мемы существовали и раньше и есть область научных знаний, специалисты в которой занимаются изучением мемов и их влиянием на нашу жизнь — меметика? Автор этой книги, журналист, популяризатор меметики и крупнейший в России исследователь мемов, Иван Кузнецов знает об этом, казалось бы, несерьезном предмете всё. Узнайте из этой книги, как информация становится мемом, почему мемы имеют такую власть над нашим разумом и почему среди ученых-меметиков так много атеистов. Прочитайте, как мемы используют в самых разных областях — от политических гонок до мошеннических схем. Узнайте историю происхождения самых странных и необычных мемов последних десятилетий. И обязательно поделитесь этой книгой с. Скрыть Показать весь текст
Исторические корни волшебной сказки» — фундаментальный труд В. Я.Проппа, переведенный на множество языков (от английского до японского), неоднократно переиздававшийся. В. Я. Пропп исследует волшебную сказку на материале русского и зарубежного фольклора. Вы. Исторические корни волшебной сказки» — фундаментальный труд В. Я.Проппа, переведенный на множество языков (от английского до японского), неоднократно переиздававшийся. В. Я. Пропп исследует волшебную сказку на материале русского и зарубежного фольклора. Вы узнаете, какие прототипы у всех сказочных героев: от Иванушки-дурочка и Василисы Прекрасной до Бабы-яги, лешего и Кощея Бессмертного. Как действия героев связаны с древними обрядами и верованиями? Какие тайны и исторические параллели скрываются в структуре любимых нами с детства сказок (от русских народных до братьев Гримм) Скрыть Показать весь текст
«Разговорная грамматика с English Spot» расскажет вам об особенностях грамматики устной речи, поможет научиться правильно выстраивать свои мысли на английском, а также овладеть приемами беглой речи и тем самым приблизиться к уровню носителей. Рекомендуется. «Разговорная грамматика с English Spot» расскажет вам об особенностях грамматики устной речи, поможет научиться правильно выстраивать свои мысли на английском, а также овладеть приемами беглой речи и тем самым приблизиться к уровню носителей. Рекомендуется использовать данное издание в качестве дополнения к основной программе обучения и применять полученные знания по назначению – для живого общения на английском вне стен учебных заведений. Скрыть Показать весь текст
Анализ характерных студенческих ошибок при разборе предложений на классическом китайском языке на уровне словосочетаний от малого к большому. Монография
Настоящая монография посвящена анализу характерных студенческих ошибок, возникающих при разборе предложений на вэньяне на уровне словосочетаний от малого к большому. Показано, что основные ошибки можно поделить на три группы: 1) неверное вычленение отдельных. Настоящая монография посвящена анализу характерных студенческих ошибок, возникающих при разборе предложений на вэньяне на уровне словосочетаний от малого к большому. Показано, что основные ошибки можно поделить на три группы: 1) неверное вычленение отдельных лексем; 2) ошибочное определение типов словосочетаний; 3) неверное вычленение словосочетаний. Исследуется взаимосвязь между переводом предложения на вэньяне и построением его структурной схемы. Анализ ошибок на схеме используется для исправления неверного перевода.
Монография рекомендуется аспирантам и докторантам, занятым исследованиями в области синтаксиса классического китайского языка, преподавателям таких дисциплин, как «Практический курс китайского языка», «История китайского языка» и «Методы и принципы лингвистического анализа текстов на китайском языке», а также их студентам. Скрыть Показать весь текст
Персонажи Достоевского — бунтари, блудницы, юродивые, донкихоты и фарисеи. Они бьются над вопросами о добре, зле, источнике страданий, о Боге, вере и отрицании. Но они не вопрошают о смерти. В произведениях она существует как физический факт, а не как. Персонажи Достоевского — бунтари, блудницы, юродивые, донкихоты и фарисеи. Они бьются над вопросами о добре, зле, источнике страданий, о Боге, вере и отрицании. Но они не вопрошают о смерти. В произведениях она существует как физический факт, а не как философская загадка. Вселенная Достоевского сама по себе является ответом на вопрос о природе бессмертия, к которому стремится человек, и ключи к нему вручаются каждому. Автор предлагает взглянуть на творчество Достоевского глазами современного читателя, знакомит с писателями и произведениями, повлиявшими на его мировоззрение, с типами и ролями персонажей, рассматривает занимающие их вопросы, прослеживает, как мысли и тексты Достоевского трансформировались и вошли в современную культуру. Скрыть Показать весь текст
Авторы на основании личного опыта и данных литературы впервые в одном издании представили обобщенные данные об особенностях течения редких форм эктопической беременности, методах диагностики и способах лечения с учетом по возможности сохранения репродуктивной. Авторы на основании личного опыта и данных литературы впервые в одном издании представили обобщенные данные об особенностях течения редких форм эктопической беременности, методах диагностики и способах лечения с учетом по возможности сохранения репродуктивной функции.
В настоящей монографии представлены такие варианты эктопической беременности, как трубная, шеечная, истмическая, интер-стициальная, яичниковая, в рудиментарном роге матки, брюшная, гетеротопическая, в рубце на матке после кесарева сечения, в культе маточной трубы, старая внематочная беременность, сочетание внематочной беременности с апоплексией яичника.
Книга рассчитана на врачей акушеров-гинекологов, специалистов ультразвуковой диагностики и студентов медицинских вузов. Скрыть Показать весь текст
В книге представлена информация о дополнительных исследованиях в педиатрии — наиболее часто используемых общеклинических, биохимических, иммунологических и других методах, изменениях при патологии. Указаны особенности функций органов и систем в детском. В книге представлена информация о дополнительных исследованиях в педиатрии — наиболее часто используемых общеклинических, биохимических, иммунологических и других методах, изменениях при патологии. Указаны особенности функций органов и систем в детском возрасте, диагностические
Лабораторно-функциональные критерии заболеваний. Материал приведен в виде таблиц, схем и иллюстраций. В пятом издании дополнены и уточнены справочные значения ряда показателей, в том числе при COVID-19; пересмотрены разделы, посвященные иммунному статусу с диагностикой аутоиммунных заболеваний, исследованиям дыхательной и пищеварительной систем.
Издание предназначено для самостоятельной работы студентов медицинских высших и средних учебных заведений, а также для клинических интернов и ординаторов, врачей-педиатров, врачей общей практики, врачей и лаборантов клинической лабораторной диагностики. Скрыть Показать весь текст

В историях Пу Сунлина, составивших эту книгу, решительно сметены границы между миром действительным и миром волшебной феерии. Это изысканные, по-настоящему странные истории, тончайшие и мудрые восточные сказки, где пороки будут наказаны, а чистые помыслы и. В историях Пу Сунлина, составивших эту книгу, решительно сметены границы между миром действительным и миром волшебной феерии. Это изысканные, по-настоящему странные истории, тончайшие и мудрые восточные сказки, где пороки будут наказаны, а чистые помыслы и деяния вознаграждены. Скрыть Показать весь текст
Перед вами настоящее полевое руководство по изучению современного города. Почти каждый элемент городской среды предстает с необычного, нового ракурса. С каждым из них связана история, которая удивит, развеселит или заставит задуматься. Роман Марс, популярный. Перед вами настоящее полевое руководство по изучению современного города. Почти каждый элемент городской среды предстает с необычного, нового ракурса. С каждым из них связана история, которая удивит, развеселит или заставит задуматься. Роман Марс, популярный подкастер, наводит свою уникальную оптику на все: от заброшенных строений и линий электропередач до деловых кварталов и исторической застройки. Привычная прогулка по городу с этой книгой превратится в настоящий аттракцион. Скрыть Показать весь текст
Каково быть птицей: о полетах и гнездовании, кормлении и пении. Как и чем живут самые известные птицы на земле
Это настоящая «птичья» книга для всех, кто увлекается жизнью пернатых, представляет новое и более глубокое понимание того, что делают обычные птицы, которых мы часто видим в своем саду, — и почему. Книга охватывает более двухсот видов и включает более 330. Это настоящая «птичья» книга для всех, кто увлекается жизнью пернатых, представляет новое и более глубокое понимание того, что делают обычные птицы, которых мы часто видим в своем саду, — и почему. Книга охватывает более двухсот видов и включает более 330 новых иллюстраций автора. Хотя в центре внимания находятся наиболее популярные птицы — голубые сойки, поползни, синицы, также исследуются некоторые редко встречающиеся виды. Увлекательные новые научные исследования бесчисленных способов адаптации птиц к изменениям окружающей среды будут интересны не только взрослым. Маленькие дети будут в восторге от больших полноцветных иллюстраций птиц. Скрыть Показать весь текст
Лучшие продажи раздела
Как говорит знаменитый приматолог и нейробиолог Роберт Сапольски, если вы хотите понять поведение человека и природу хорошего или плохого поступка, вам придется разобраться буквально во всем — и в том, что происходило за секунду до него, и в том, что было. Как говорит знаменитый приматолог и нейробиолог Роберт Сапольски, если вы хотите понять поведение человека и природу хорошего или плохого поступка, вам придется разобраться буквально во всем — и в том, что происходило за секунду до него, и в том, что было миллионы лет назад. В книге автор поэтапно — можно сказать, в хронологическом разрезе — и очень подробно рассматривает огромное количество факторов, влияющих на наше поведение. Как работает наш мозг? За что отвечает миндалина, а за что нам стоит благодарить лобную кору? Что «ненавидит» островок? Почему у лондонских таксистов увеличен гиппокамп? Как связаны длины указательного и безымянного пальцев и количество внутриутробного тестостерона? Чем с точки зрения нейробиологии подростки отличаются от детей и взрослых? Бывают ли «чистые» альтруисты? В чем разница между прощением и примирением? Существует ли свобода воли? Как сложные социальные связи влияют на наше поведение и принятие решений? И это лишь малая часть вопросов. Скрыть Показать весь текст
Если вы хотите научиться разбираться в искусстве — эта книга для вас. Она поможет вам понять, как искусство развивается, как оно устроено, и заговорить на языке искусства. С ней вы сможете разобраться в истории европейского искусства, научиться различать. Если вы хотите научиться разбираться в искусстве — эта книга для вас. Она поможет вам понять, как искусство развивается, как оно устроено, и заговорить на языке искусства. С ней вы сможете разобраться в истории европейского искусства, научиться различать стили, направления и течения, а также понимать причины появления в искусстве тех или иных явлений. .Книга написана вместе с Level One — крупнейшим лекторием Москвы, который помогает разобраться в сложных темах, от искусства и астрономии до развития памяти и практикумов по стилю. Автор книги — Алина Аксенова, лектор Level One, искусствовед, филолог и преподаватель истории искусств. Скрыть Показать весь текст
Оливер Сакс — всемирно известный британский невролог, автор десятка популярных книг, переведенных на множество языков и ставших международными бестселлерами. .«Человек, который принял жену за шляпу» — книга-сенса-ция, написанная Оливером Саксом еще в 1971 году. Оливер Сакс — всемирно известный британский невролог, автор десятка популярных книг, переведенных на множество языков и ставших международными бестселлерами. .«Человек, который принял жену за шляпу» — книга-сенса-ция, написанная Оливером Саксом еще в 1971 году и выдержавшая с тех пор десятки переизданий только на английском языке, не говоря уже о многочисленных переводах. Это истории современных людей, пытающихся побороть серьезные и необычные нарушения психики и борющихся за выживание в условиях, невообразимых для здоровых людей, и о мистиках прошлого, одержимых видениями, которые современная наука диагностирует как проявление тяжелых неврозов. Странные, труднопостижимые отношения между мозгом и сознанием Сакс объясняет доступно, живо и интересно. . Скрыть Показать весь текст
Соединив естественнонаучный подход с историческим, доктор Юваль Харари ставит под сомнение многие общепринятые идеи, обнаруживает связи между событиями прошлого и нашими сегодняшними опасениями и рассматривает отдельные события в едином глобальном контексте. Соединив естественнонаучный подход с историческим, доктор Юваль Харари ставит под сомнение многие общепринятые идеи, обнаруживает связи между событиями прошлого и нашими сегодняшними опасениями и рассматривает отдельные события в едином глобальном контексте. Прослеживая, как развивающееся человечество влияло на глобальную экосистему и анализируя судьбы империй, доктор Харари заглядывает в будущее. За последние несколько десятилетий мы научились изменять закон естественного отбора, управлявший жизнью на протяжении 4 миллиардов лет, и у нас впервые появляется способность пересоздавать не только окружающий мир, но и самих себя. Кем же мы хотим стать, и куда это нас приведет? Скрыть Показать весь текст
Сто тысяч лет назад Homo sapiens был одним из как минимум шести видов человека, живших на этой планете, — ничем не примечательным животным, которое играло в экосистеме роль не большую, чем гориллы, светлячки или медузы. Но около семидесяти тысяч лет назад. Сто тысяч лет назад Homo sapiens был одним из как минимум шести видов человека, живших на этой планете, — ничем не примечательным животным, которое играло в экосистеме роль не большую, чем гориллы, светлячки или медузы. Но около семидесяти тысяч лет назад загадочное изменение когнитивных способностей Homo sapiens превратило его в хозяина планеты и кошмар экосистемы. Как человек разумный сумел покорить мир? Что стало с другими видами человека? Когда и почему появились деньги, государства и религия? Как возникали и рушились империи? Почему почти все общества ставили женщин ниже мужчин? Как наука и капитализм стали господствующими вероучениями современной эры? Становились ли люди с течением времени счастливее? Какое будущее нас ожидает?
Юваль Харари показывает, как ход истории формировал человеческое общество и действительность вокруг него. Его книга прослеживает связь между событиями прошлого и проблемами современности и заставляет читателя пересмотреть все устоявшиеся представления об. Скрыть Показать весь текст
Более 10 лет первое издание этой книги считалось одним из лучших практических руководств по программированию. Сейчас эта книга полностью обновлена с учетом современных тенденций и технологий и дополнена сотнями новых примеров, иллюстрирующих искусство и науку. Более 10 лет первое издание этой книги считалось одним из лучших практических руководств по программированию. Сейчас эта книга полностью обновлена с учетом современных тенденций и технологий и дополнена сотнями новых примеров, иллюстрирующих искусство и науку программирования. Опираясь на академические исследования, с одной стороны, и практический опыт коммерческих разработок ПО — с другой, автор синтезировал из самых эффективных методик и наиболее эффективных принципов ясное прагматичное руководство. Каков бы ни был ваш профессиональный уровень, с какими бы средствами разработками вы ни работали, какова бы ни была сложность вашего проекта, в этой книге вы найдете нужную информацию, она заставит вас размышлять и поможет создать совершенный код. Изложенные в книге методики и стратегии помогут вам:проектировать с минимальной сложностью и максимальной продуктивностью извлекать выгоду из групповой разработки применять методики защитного программирования, позволяющие избежать ошибок. Скрыть Показать весь текст
Даже плохой программный код может работать. Однако если код не является «чистым», это всегда будет мешать развитию проекта и компании-разработчика, отнимая значительные ресурсы на его поддержку и «укрощение». Эта книга посвящена хорошему программированию. Даже плохой программный код может работать. Однако если код не является «чистым», это всегда будет мешать развитию проекта и компании-разработчика, отнимая значительные ресурсы на его поддержку и «укрощение».
Эта книга посвящена хорошему программированию. Она полна реальных примеров кода. Мы будем рассматривать код с различных направлений: сверху вниз, снизу вверх и даже изнутри. Прочитав книгу, вы узнаете много нового о коде. Более того, вы научитесь отличать хороший код от плохого. Вы узнаете, как писать хороший код и как преобразовать плохой код в хороший.
Книга состоит из трех частей. В первой части излагаются принципы, паттерны и приемы написания чистого кода; приводится большой объем примеров кода. Вторая часть состоит из практических сценариев нарастающей сложности. Каждый сценарий представляет собой упражнение по чистке кода или преобразованию проблемного кода в код с меньшим количеством проблем. Третья часть книги — концентрированное выражение ее сути. Она состоит из одной. Скрыть Показать весь текст
Мы созданы нашими генами. Мы, животные, существуем, чтобы сохранить их, и служим лишь машинами, обеспечивающими их выживание. Мир эгоистичного гена — это мир жестокой конкуренции, безжалостной эксплуатации и обмана. Ну а как же акты альтруизма, наблюдаемые в. Мы созданы нашими генами. Мы, животные, существуем, чтобы сохранить их, и служим лишь машинами, обеспечивающими их выживание. Мир эгоистичного гена — это мир жестокой конкуренции, безжалостной эксплуатации и обмана. Ну а как же акты альтруизма, наблюдаемые в природе: пчелы, совершающие самоубийство, когда они жалят врага, чтобы защитить улей, или птицы, рискующие жизнью, чтобы предупредить стаю о приближении ястреба? Противоречит ли это фундаментальному закону об эгоистичности гена? Ни в коем случае! Докинз показывает, что эгоистичный ген — это еще и хитрый ген. И он лелеет надежду, что вид Homo sapiens — единственный на всем земном шаре — в силах взбунтоваться против намерений эгоистичного гена.
Перевод сверен по юбилейному английскому изданию 2006 года. Скрыть Показать весь текст
Книга молодого научного журналиста Аси Казанцевой — об «основных биологических ловушках, которые мешают нам жить счастливо и вести себя хорошо». Опираясь по большей части на авторитетные научные труды и лишь иногда — на личный опыт, автор увлекательно и. Книга молодого научного журналиста Аси Казанцевой — об «основных биологических ловушках, которые мешают нам жить счастливо и вести себя хорошо». Опираясь по большей части на авторитетные научные труды и лишь иногда — на личный опыт, автор увлекательно и доступно рассказывает, откуда берутся вредные привычки, почему в ноябре так трудно работать и какие вещества лежат в основе «химии любви». Скрыть Показать весь текст
Основы стохастической финансовой математики. Том 1. Факты. Модели (комплект из 2 книг)
Настоящая книга призвана дать весьма широкое представление о предмете финансовой математики, ее истории, основных этапах становления ее теорий, теории арбитража и расчетов в стохастических финансовых моделях. В книге уделяется значительное внимание не только моделям с дискретным временем, но и моделям в непрерывном времени, включая нужные в финансовой математике темы: теорема Гирсанова, преобразование Эшера, формулы Башелье и Блэка–Шоулса для расчетов опционов европейского типа и др.
Издание предназначено для подготовки учащихся 11-х классов к ЕГЭ по биологии. Теория по предмету приведена в полном объеме и соответствует кодификатору элементов содержания и требований к уровню подготовки выпускников общеобразовательных учреждений для. Издание предназначено для подготовки учащихся 11-х классов к ЕГЭ по биологии. Теория по предмету приведена в полном объеме и соответствует кодификатору элементов содержания и требований к уровню подготовки выпускников общеобразовательных учреждений для проведения единого государственного экзамена. Материал изложен в той последовательности, в которой он будет представлен на реальном экзамене, соответствует темам, проверяемым на ЕГЭ, и четко распределен по заданиям (от 1 до 28). Перед каждым теоретическим блоком приводится разбор экзаменационных заданий с подробными рекомендациями по решению. Для проверки знаний в конце книги дано 5 тренировочных вариантов с ответами. Издание может быть использовано учащимися для подготовки к экзамену, учителями и репетиторами для организации учебного процесса и выявления реального уровня подготовки выпускников. Скрыть Показать весь текст
В сборник вошли основополагающие труды всемирно известного философа, психолога и психиатра Рэймонда Моуди: «Жизнь после жизни» — первое исследование так называемого околосмертного опыта, или околосмертных переживаний. Автор проанализировал более ста отчетов. В сборник вошли основополагающие труды всемирно известного философа, психолога и психиатра Рэймонда Моуди:
«Жизнь после жизни» — первое исследование так называемого околосмертного опыта, или околосмертных переживаний. Автор проанализировал более ста отчетов пациентов, переживших клиническую смерть, и выделил общие мотивы, повторяющиеся в их рассказах. Этот мировой бестселлер, впервые опубликованный в 1975 году, произвел настоящую революцию в мировом сознании, радикально изменив отношение общества, в том числе врачей и ученых, к смерти и умиранию.
«Свет вдали» — продолжение многолетних исследований жизни после жизни: ответы на вопросы читателей, наблюдения медицинских работников, задокументированные случаи околосмертного опыта и, конечно, новые научные изыскания. Как последние открытия в медицине, психиатрии и социологии приближают нас к разгадке тайны жизни и смерти?
«Жизнь после утраты» — всеобъемлющее руководство, адресованное тем, кто столкнулся со смертью родных и близких людей. Скрыть Показать весь текст
Все любят мемы. Если вы не скроллите ленту новостей в соцсетях в поиске свежих мемов, то точно получаете их от друзей и родственников в мессенджерах или узнаете о них от коллег. Вы думаете, что мемы появились недавно, с внедрением в нашу жизнь. Все любят мемы. Если вы не скроллите ленту новостей в соцсетях в поиске свежих мемов, то точно получаете их от друзей и родственников в мессенджерах или узнаете о них от коллег. Вы думаете, что мемы появились недавно, с внедрением в нашу жизнь интернет-технологий? А что вы скажете, если узнаете, что мемы существовали и раньше и есть область научных знаний, специалисты в которой занимаются изучением мемов и их влиянием на нашу жизнь — меметика? Автор этой книги, журналист, популяризатор меметики и крупнейший в России исследователь мемов, Иван Кузнецов знает об этом, казалось бы, несерьезном предмете всё. Узнайте из этой книги, как информация становится мемом, почему мемы имеют такую власть над нашим разумом и почему среди ученых-меметиков так много атеистов. Прочитайте, как мемы используют в самых разных областях — от политических гонок до мошеннических схем. Узнайте историю происхождения самых странных и необычных мемов последних десятилетий. И обязательно поделитесь этой книгой с. Скрыть Показать весь текст
Исторические корни волшебной сказки» — фундаментальный труд В. Я.Проппа, переведенный на множество языков (от английского до японского), неоднократно переиздававшийся. В. Я. Пропп исследует волшебную сказку на материале русского и зарубежного фольклора. Вы. Исторические корни волшебной сказки» — фундаментальный труд В. Я.Проппа, переведенный на множество языков (от английского до японского), неоднократно переиздававшийся. В. Я. Пропп исследует волшебную сказку на материале русского и зарубежного фольклора. Вы узнаете, какие прототипы у всех сказочных героев: от Иванушки-дурочка и Василисы Прекрасной до Бабы-яги, лешего и Кощея Бессмертного. Как действия героев связаны с древними обрядами и верованиями? Какие тайны и исторические параллели скрываются в структуре любимых нами с детства сказок (от русских народных до братьев Гримм) Скрыть Показать весь текст
«Разговорная грамматика с English Spot» расскажет вам об особенностях грамматики устной речи, поможет научиться правильно выстраивать свои мысли на английском, а также овладеть приемами беглой речи и тем самым приблизиться к уровню носителей. Рекомендуется. «Разговорная грамматика с English Spot» расскажет вам об особенностях грамматики устной речи, поможет научиться правильно выстраивать свои мысли на английском, а также овладеть приемами беглой речи и тем самым приблизиться к уровню носителей. Рекомендуется использовать данное издание в качестве дополнения к основной программе обучения и применять полученные знания по назначению – для живого общения на английском вне стен учебных заведений. Скрыть Показать весь текст
Анализ характерных студенческих ошибок при разборе предложений на классическом китайском языке на уровне словосочетаний от малого к большому. Монография
Настоящая монография посвящена анализу характерных студенческих ошибок, возникающих при разборе предложений на вэньяне на уровне словосочетаний от малого к большому. Показано, что основные ошибки можно поделить на три группы: 1) неверное вычленение отдельных. Настоящая монография посвящена анализу характерных студенческих ошибок, возникающих при разборе предложений на вэньяне на уровне словосочетаний от малого к большому. Показано, что основные ошибки можно поделить на три группы: 1) неверное вычленение отдельных лексем; 2) ошибочное определение типов словосочетаний; 3) неверное вычленение словосочетаний. Исследуется взаимосвязь между переводом предложения на вэньяне и построением его структурной схемы. Анализ ошибок на схеме используется для исправления неверного перевода.
Монография рекомендуется аспирантам и докторантам, занятым исследованиями в области синтаксиса классического китайского языка, преподавателям таких дисциплин, как «Практический курс китайского языка», «История китайского языка» и «Методы и принципы лингвистического анализа текстов на китайском языке», а также их студентам. Скрыть Показать весь текст
Персонажи Достоевского — бунтари, блудницы, юродивые, донкихоты и фарисеи. Они бьются над вопросами о добре, зле, источнике страданий, о Боге, вере и отрицании. Но они не вопрошают о смерти. В произведениях она существует как физический факт, а не как. Персонажи Достоевского — бунтари, блудницы, юродивые, донкихоты и фарисеи. Они бьются над вопросами о добре, зле, источнике страданий, о Боге, вере и отрицании. Но они не вопрошают о смерти. В произведениях она существует как физический факт, а не как философская загадка. Вселенная Достоевского сама по себе является ответом на вопрос о природе бессмертия, к которому стремится человек, и ключи к нему вручаются каждому. Автор предлагает взглянуть на творчество Достоевского глазами современного читателя, знакомит с писателями и произведениями, повлиявшими на его мировоззрение, с типами и ролями персонажей, рассматривает занимающие их вопросы, прослеживает, как мысли и тексты Достоевского трансформировались и вошли в современную культуру. Скрыть Показать весь текст
Авторы на основании личного опыта и данных литературы впервые в одном издании представили обобщенные данные об особенностях течения редких форм эктопической беременности, методах диагностики и способах лечения с учетом по возможности сохранения репродуктивной. Авторы на основании личного опыта и данных литературы впервые в одном издании представили обобщенные данные об особенностях течения редких форм эктопической беременности, методах диагностики и способах лечения с учетом по возможности сохранения репродуктивной функции.
В настоящей монографии представлены такие варианты эктопической беременности, как трубная, шеечная, истмическая, интер-стициальная, яичниковая, в рудиментарном роге матки, брюшная, гетеротопическая, в рубце на матке после кесарева сечения, в культе маточной трубы, старая внематочная беременность, сочетание внематочной беременности с апоплексией яичника.
Книга рассчитана на врачей акушеров-гинекологов, специалистов ультразвуковой диагностики и студентов медицинских вузов. Скрыть Показать весь текст
В книге представлена информация о дополнительных исследованиях в педиатрии — наиболее часто используемых общеклинических, биохимических, иммунологических и других методах, изменениях при патологии. Указаны особенности функций органов и систем в детском. В книге представлена информация о дополнительных исследованиях в педиатрии — наиболее часто используемых общеклинических, биохимических, иммунологических и других методах, изменениях при патологии. Указаны особенности функций органов и систем в детском возрасте, диагностические
Лабораторно-функциональные критерии заболеваний. Материал приведен в виде таблиц, схем и иллюстраций. В пятом издании дополнены и уточнены справочные значения ряда показателей, в том числе при COVID-19; пересмотрены разделы, посвященные иммунному статусу с диагностикой аутоиммунных заболеваний, исследованиям дыхательной и пищеварительной систем.
Издание предназначено для самостоятельной работы студентов медицинских высших и средних учебных заведений, а также для клинических интернов и ординаторов, врачей-педиатров, врачей общей практики, врачей и лаборантов клинической лабораторной диагностики. Скрыть Показать весь текст
В историях Пу Сунлина, составивших эту книгу, решительно сметены границы между миром действительным и миром волшебной феерии. Это изысканные, по-настоящему странные истории, тончайшие и мудрые восточные сказки, где пороки будут наказаны, а чистые помыслы и. В историях Пу Сунлина, составивших эту книгу, решительно сметены границы между миром действительным и миром волшебной феерии. Это изысканные, по-настоящему странные истории, тончайшие и мудрые восточные сказки, где пороки будут наказаны, а чистые помыслы и деяния вознаграждены. Скрыть Показать весь текст
Перед вами настоящее полевое руководство по изучению современного города. Почти каждый элемент городской среды предстает с необычного, нового ракурса. С каждым из них связана история, которая удивит, развеселит или заставит задуматься. Роман Марс, популярный. Перед вами настоящее полевое руководство по изучению современного города. Почти каждый элемент городской среды предстает с необычного, нового ракурса. С каждым из них связана история, которая удивит, развеселит или заставит задуматься. Роман Марс, популярный подкастер, наводит свою уникальную оптику на все: от заброшенных строений и линий электропередач до деловых кварталов и исторической застройки. Привычная прогулка по городу с этой книгой превратится в настоящий аттракцион. Скрыть Показать весь текст
Каково быть птицей: о полетах и гнездовании, кормлении и пении. Как и чем живут самые известные птицы на земле
Это настоящая «птичья» книга для всех, кто увлекается жизнью пернатых, представляет новое и более глубокое понимание того, что делают обычные птицы, которых мы часто видим в своем саду, — и почему. Книга охватывает более двухсот видов и включает более 330. Это настоящая «птичья» книга для всех, кто увлекается жизнью пернатых, представляет новое и более глубокое понимание того, что делают обычные птицы, которых мы часто видим в своем саду, — и почему. Книга охватывает более двухсот видов и включает более 330 новых иллюстраций автора. Хотя в центре внимания находятся наиболее популярные птицы — голубые сойки, поползни, синицы, также исследуются некоторые редко встречающиеся виды. Увлекательные новые научные исследования бесчисленных способов адаптации птиц к изменениям окружающей среды будут интересны не только взрослым. Маленькие дети будут в восторге от больших полноцветных иллюстраций птиц. Скрыть Показать весь текст
Как работает наш мозг.
Www. chitai-gorod. ru
16.11.2019 13:41:37
2019-03-25 15:07:22
Источники:
Https://www. chitai-gorod. ru/catalog/book/2835116/
Слайд 1
Описание слайда:
Основы финансовых вычислений. Задачи
Различные способы вычисления процентов
Дисконтирование
Учёт инфляции
Потоки платежей
Ренты
Слайд 2
Описание слайда:
Задача 1
Какова простая ставка процентов, при которой первоначальный капитал в размере 130000 руб., достигнет через 100 дней 155000 руб.? Число дней году считается приближённо и равно 360. Ответ привести с точностью до 0,01%.
Решение. Воспользуемся формулой
. Подставив данные задачи
; , получим
Слайд 3
Описание слайда:
Решение задачи 1. Задача 2.
; ; ;
; i = 69,23%.
Задача 2. Ссуда 700000 руб. выдана на квартал по простой ставке процентов 15% годовых. Определить наращенную сумму.
Решение. Используя формулу простых процентов для вычисления наращенной суммы, получим = 726250.
Слайд 4
Описание слайда:
Задача 3
Найти сумму накопленного долга и проценты, если ссуда 180000 руб. выдана на три года под простые 18% годовых. Во сколько раз увеличится наращенная сумма при увеличении ставки на 2%?
Решение. Вычислим сумму накопленного долга S как наращенную сумму по формуле простых процентов .
S
Слайд 5
Описание слайда:
Решение задачи 3. Задача 4
Проценты равны . При ставке 18% + 2% = 20% наращенная сумма равна = 180000∙(1 + 3∙0,2) = 288000. Наращенная сумма увеличивается в
= 1,03896 раза.
Задача 4. Определить простую ставку процентов, при которой первоначальный капитал в размере 122000 руб., достигнет через 120 дней величины 170000 руб. Временная база К=360.
Слайд 6
Описание слайда:
Решение задачи 4. Задача 5
. Воспользуемся формулой наращения по простой процентной ставке . Найдём . Подставив условия задачи, получим ; ;
или 118,03%.
Задача 5. Определить период, за который начальный капитал в размере 46000 руб. вырастет до 75000 руб., если ставка простых процентов равна 15% годовых.
5
Слайд 7
Описание слайда:
Решение задачи 5. Задача 6
Воспользуемся формулой наращения по простой процентной ставке . Подставив условия задачи, получим
Задача 6. Ссуда 150000 руб. выдана на 4 года под 20% годовых (простые проценты). Во сколько раз больше наращенная сумма по сравнению со ссудой?
Слайд 8
Описание слайда:
Решение задачи 6. Задача 7
Найдём наращенную сумму по формуле простых процентов
Эта сумма раз больше ссуды, что как раз равно множителю наращения.
Задача 7. В банк 7 февраля на депозит положили сумму 20000 у.е. под 11% годовых по схеме сложных процентов. Какую сумму вкладчик снимет 1 октября?
Слайд 9
Описание слайда:
Решение задачи 7. Задача 8
Найдём время t. 7 февраля день №38, 1октября день №274, число дней равно 274 – 38 = 236, время (в годах) равно . Найдём искомую сумму как наращенную величину по формуле сложных процентов .
Задача 8. Вклад на 80000 руб., открытый в банке на 10 месяцев, принес вкладчику 7000 руб. Под какой простой (сложный) процент годовых был открыт вклад?
Слайд 10
Описание слайда:
Решение задачи 8.
Для вычисления сложного процента применим формулу . Подставив данные задачи, получим уравнение 80000 + 7000 =
= Откуда ; ;
или 10,59%. Для вычисления простого процента применим формулу Подставив данные задачи, получим уравнение 80000+7000 = 80000∙(1+10/12∙i). Откуда ; или 10,5%.
Слайд 11
Описание слайда:
Задачи 9, 10
Задача 9. Чему равен процентный платеж, если кредит 170000 руб. взят на 7 месяцев под сложных 17% годовых?
Решение. Процентный платеж равен разности между наращенной суммой и величиной кредита
Задача 10. Ставка по годовому депозиту равна 8%. Какую ставку годовых процентов нужно назначить на полугодовой депозит,
Слайд 12
Описание слайда:
Задачи 10, 11
чтобы последовательное переоформление полугодового депозита привело бы к такому же результату, что и при использовании годового депозита? (К=360)
Решение. . Следовательно
или 7,85%.
Задача 11. Заемщик должен уплатить 80000 руб. через 65 дней. Кредит выдан под 19% годовых (простые проценты).
Слайд 13
Описание слайда:
Задачи 11, 12
Какова первоначальная сумма долга и дисконт (К=360)?
Решение. . Следовательно
=77346,58. Дисконт равен D = 80000 – 77346,58 = 2653,42.
Задача 12. На счет в банке кладется сумма в размере 20000 руб. на 4 года под 11% годовых по схеме простых процентов с дальнейшей пролонгацией на последующие 2 года под 6% годовых по той
Слайд 14
Описание слайда:
Задача 12
же схеме. Найти размер вклада через 6 лет. Определить наращенную сумму, если вклад изымается через 4 года и кладется на новый счет на 2 года по той же схеме.
Решение. а) 20000∙(1 + 4∙0,11 + 2∙0,06) = 31200
б) 20000∙(1 + 4∙0,11)∙(1 + 2∙0,06) = 32256
Слайд 15
Описание слайда:
Задача 13
В банк положен депозит в размере 2400 руб. под 7% годовых по схеме сложных процентов. Найти величину депозита через три года при начислении процентов 1, 4, 6, 12 раз в году и в случае непрерывного начисления процентов.
Решение. а) = 2940,1;
б) ; в)
г) ; д)
Слайд 16
Описание слайда:
Задача 14
Клиент поместил в банк вклад в сумме 18000 руб. под 8,5% годовых с ежемесячной выплатой процентов. Какую сумму клиент будет получать каждый месяц, если начисление производится по формуле простых процентов?
Решение. Искомая сумма равна величине 18000∙0, 085:12 = 127,5.
Слайд 17
Описание слайда:
Задача 15
На годовом депозите можно получить 12% годовых, а на полугодовом — 11,5% годовых. Что выгоднее — положить средства на годовой депозит, или на полугодовой депозит с пролонгацией на тех же условиях? Чему будут равны проценты в обоих случаях при сумме депозита 25000 руб.?
Решение. Наращенная сумма на годовом депозите .Наращенная сумма на полугодовом депозите .
Слайд 18
Описание слайда:
Задача 16
В банк положена сумма 40000 у.е. сроком на 2 года по ставке 10% годовых. Найти наращенную сумму, величину полученного процента и эффективную процентную ставку для следующих вариантов начисления процентов: а) ежеквартального; б) ежемесячного.
Решение. а) наращенная сумма
; процентные деньги I = 8736,12;
Слайд 19
Описание слайда:
Решение задачи 16. Задача 17
эффективная процентная ставка
или 10,38 %;
б) ; I = 8815,64;
или 10,47%.
Задача 17. За какой период первоначальный капитал в размере 40000 руб. вырастет до 75000 руб. при простой ставке 15% годовых?
Слайд 20
Описание слайда:
Решение задачи 17. Задача 18
Для простых процентов выполняется соотношение 75000 = 40000∙(1 + 0,15n). Следовательно 0,15n = ; n =
Для сложных процентов выполняется соотношение 75000 .
Следовательно ;
Задача 18 . В банк положена сумма 150000 руб. сроком на 6 лет по ставке 14% годовых. Найти наращенную сумму, величину полученного процента и эффективную
Слайд 21
Описание слайда:
Задача 18
процентную ставку для следующих вариантов начисления процентов: а) полугодового; б) ежеквартального; в) ежемесячного; г) непрерывного при силе роста 14%.
Решение. а) наращенная сумма равна
; величина полученного процента равна I = 187828,74; эффективная процентная ставка равна
.
Слайд 22
Описание слайда:
Решение задачи 18
б) наращенная сумма равна ; величина полученного процента равна I = 192499,27; эффективная процентная ставка равна .
в) наращенная сумма равна
; величина полученного процента равна I = 195769,74; эффективная процентная ставка равна
.
Слайд 23
Описание слайда:
Решение задачи 18. Задача 19
г) наращенная сумма равна
; величина полученного процента равна I = 197455,05; эффективная процентная ставка равна
Задача 19. На сумму долга в течение 8 лет начисляются проценты по ставке 11% годовых. Во сколько раз возрастет наращенная сумма, если проценты будут капитализироваться ежемесячно? Ежеквартально? Непрерывно?
.
Слайд 24
Описание слайда:
Решение задачи 19
Наращенная сумма при ежегодной капитализации равна .
Наращенная сумма при ежемесячной капитализации равна , что в
раза больше, чем при годовой капитализации.
Наращенная сумма при ежеквартальной капитализации равна , что в раза больше, чем при годовой капитализации.
Слайд 25
Описание слайда:
Решение задачи 19. Задача 20
Наращенная сумма при непрерывной капитализации равна , что в
раза больше, чем при годовой капитализации.
Задача 20. На какой срок необходимо положить в банк 12000 руб., чтобы накопить 15000 руб., если банк принимает вклады под простые (сложные) 8% годовых?
Решение. Простые проценты. Воспользуемся формулой ;
Слайд 26
Описание слайда:
Решение задачи 20.Задача 21
1200(1 + 0,08n) = 1500; = 3,125.
Сложные проценты. Воспользуемся формулой ; ; ;
.
Задача 21. Банк принимает депозиты на сумму 500000 руб. на следующих условиях: а) под 10% годовых с ежеквартальным начислением процентов;
Слайд 27
Описание слайда:
Задача 21
б) под 10% годовых с полугодовым начислением процентов; в) под 11,5% годовых (во всех трех случаях проценты капитализируются). Выберите оптимальную схему вложения денежных средств.
Решение. Воспользуемся формулой
а) ;
б) ;
в) . Самым выгодным депозитом является депозит в).
Слайд 28
Описание слайда:
Задача 22
Компания получила кредит на три года в размере 234000 руб. с условием возврата 456000 руб. Определить процентную ставку для случаев простого и сложного процента.
Решение. Для простого процента имеем соотношение 456000 = 234000∙(1 + 3i). Откуда ; или 32,75%.
Для сложного процента ;
или 24,91%.
Слайд 29
Описание слайда:
Задача 23
Вклад открыт под 14% простых годовых. На него начислен процентный платеж в сумме 1500 руб. Найдите величину вклада, если он был открыт на: а) 10 лет, б) 1 год, в) 6 месяцев, г) 10 дней. Временная база K — 365 дней.
Решение. Воспользуемся формулой для вычисления процентного платежа .
а) ; ;
Слайд 30
Описание слайда:
Решение задачи 23. Задача 24
б) 1500 = ; ;
в) ; .
Задача 24. Вексель стоимостью 100000 руб. учитывается за 4 года до погашения по сложной учетной ставке 15% годовых. Найдите сумму, получаемую векселедержателем, и величину дисконта.
Решение. Искомая сумма равна
.
Слайд 31
Описание слайда:
Задача 25.
Клиент имеет вексель на 16000 у.е., который он хочет учесть 10.01.2009 г. в банке по сложной учетной ставке 8%. Какую сумму он получит, если срок до погашения 10.07.2009 г.?
Решение. Найдём время t до погашения векселя. 10,01 – день №10; 10,07 – день №191; число дней равно 191 – 10 = 181; . Сумма, полученная векселедержателем равна .
Слайд 32
Описание слайда:
Задача 26
Предприятие получило кредит на один год в размере 7 млн. руб. с условием возврата 7,77 млн. руб. Рассчитайте процентную и учетную ставку.
Решение. Процентная ставка вычисляется по формуле . Откуда ;
; или 11%.
Учётная ставка вычисляется по формуле
. Откуда 7000000 = 7770000 ;
Слайд 33
Описание слайда:
Решение задачи 26. Задача 27
; или 9,9%.
Задача 27. Банк учитывает вексель по номинальной учетной ставке 10% с ежемесячным начислением процентов. Найти сложную учетную ставку, при которой доход банка не изменился.
Решение. Искомая учётная ставка является эффективной учётной ставкой и вычисляется по формуле .
или 9,55%.
Слайд 34
Описание слайда:
Задача 28. Задача 29
Задача 28. Вексель стоимостью 550 тыс. руб. учитывается за три года до погашения по сложной учетной ставке 12% годовых. Найти сумму, которую получит векселедержатель, и величину дисконта.
Решение. Искомая сумма равна
.
Задача 29. Клиент имеет вексель на 20000 руб., который он хочет учесть 24.04.2011 г. в банке по сложной учетной ставке 10%.
Слайд 35
Описание слайда:
Задачи 29, 30
Какую сумму он получит, если срок погашения 12.09.2011 г.?
Решение. Найдём время t с момента учёта до момента погашения векселя. 24.04 – день №144; 12.09 –день № 255; число дней 255 – 114 = 141; . Сумма, полученная клиентом равна
Задача 30. Номинальная учетная ставка равна 10%. При этом проценты начисляются ежеквартально. Найти эффективную учетную ставку.
Слайд 36
Описание слайда:
Решение задачи 30. Задача31
Эффективная учётная ставка равна
или 9,63%.
Задача 31. Что выгоднее, положить 1000 у.е. в банк на год под 8% годовых или купить за 1000 у.е. вексель с номиналом 1100 у.е. и погашением через год? Чему равна доходность покупки векселя, измеренная в виде годовой ставки процентов?
Слайд 37
Описание слайда:
Решение задачи 31. Задача 32
Наращенная сумма при вкладе в банк равна . Покупка векселя с номиналом 1100 выгоднее. Доходность покупки векселя вычисляется по формуле ; 1100 = 1000∙(1 +i); 1 + i = 1,1; i =0,1 или 10%.
Задача 32. Вексель куплен за 200 дней до его погашения. На момент покупки рыночная простая учетная ставка составляла 7% годовых.
Слайд 38
Описание слайда:
Задача 32
Через 5 дней вексель продали по учетной ставке 6% годовых. Оцените эффективность данной финансовой операции в виде ставки простых процентов. Временная база K = 365 дней.
Решение. Вексель куплен за сумму
. Вексель продан за сумму . Эффективность операции выражается по формуле . Откуда
; ; или 47,83% .
Слайд 39
Описание слайда:
Задачи 33, 34
Задача 33. Найти сложную процентную ставку , эквивалентную непрерывной ставке 8%. Ответ привести с точностью до 0,01%.
Решение. Искомая ставка процентов равна
или 8,33%.
Задача 34. Найти сложную процентную ставку , эквивалентную простой ставке 10%.
Решение. Используя формулу эквивалентности сложной и простой
Слайд 40
Описание слайда:
Решение задачи 34. Задача 35.
процентных ставок, получим
или 8,45%.
Задача 35. Найти простую процентную ставку , эквивалентную сложной ставке 11% для временного интервала 1,5 года.
Решение. Искомая простая ставка равна
или 11,3%.
Слайд 41
Описание слайда:
Задача 36
Найти непрерывную процентную ставку , эквивалентную простой ставке в 15% для временного интервала в 5 лет.
Решение. Используя равенство множителей наращения , найдём непрерывную ставку процентов (силу роста ) =
или 11,19%.
Слайд 42
Описание слайда:
Задача 37
Найти простую процентную ставку , эквивалентную сложной ставке в 15% для временного интервала в 5 лет при ежемесячном начислении процентов.
Решение. Используя равенство множителей наращения ,
найдём простую ставку процентов
или 22,14%.
Слайд 43
Описание слайда:
Задача 38
Номинальная процентная ставка составляет 12% годовых при годовом темпе инфляции 4%. Чему равна реальная ставка с учётом инфляции. Чему равна эффективная процентная ставка, если проценты начисляются ежемесячно? ежедневно? ежеквартально?
Решение. Реальная ставка с учётом инфляции равна или
3,7%. Эффективная процентная ставка вычисляется по формуле
Слайд 44
Описание слайда:
Решение задачи 38.Задача 39
При ежемесячном начислении процентов
.
При ежедневном начислении процентов
.
При ежеквартальном начислении процентов .
Задача 39. Номинальная процентная ставка составляет 15% годовых. Чему равна
Слайд 45
Описание слайда:
Задача 39
эффективная процентная ставка, если проценты начисляются ежемесячно? ежедневно? ежеквартально?
Решение. Воспользуемся формулой
При ежемесячном начислении процентов
.
При ежедневном начислении процентов
Слайд 46
Описание слайда:
Решение задачи 39. Задача 40
При ежеквартальном начислении процентов .
Задача 40. Ставка процентов составляет 10% годовых. Месячный темп инфляции в первом полугодии был постоянен и составил 2%, во втором полугодии — 3%. Во сколько раз реальная наращенная сумма превзойдёт сумму депозита за год?
Слайд 47
Описание слайда:
Решение задачи 40. Задача 41
Темп инфляции за год составляет величину
. Реальная процентная ставка равна . Реальная сумма депозита за год возрастёт в 1 + r = 1,047 раза.
Задача 41. Темп инфляции за период
равен 0,75. Темпы инфляции за периоды соответственно, составляют геометрическую прогрессию со
Слайд 48
Описание слайда:
Задача 41
знаменателем 0,9. Найти темп инфляции за каждый период.
Решение. Темпы инфляций равны , ,
. . Следовательно .
f(0,22) = -28; f(0,23) = 11,1. Следовательно с точностью до 0,005 или 22,5%.
Слайд 49
Описание слайда:
Задача 42
Темп инфляции за период равен 0,8. Темпы инфляции за периоды
соответственно, составляют арифметическую прогрессию с разностью 0,01. Найти темп инфляции за каждый период.
Решение. Воспользуемся формулой вычисления инфляции за несколько периодов .
Слайд 50
Описание слайда:
Решение задачи 42.Задача 43
.
, . Следовательно, с точностью до 0,005 или 20,5%.
Задача 43. Темп инфляции за первый период равен 0,37. Темп инфляции за второй период на 55% выше, чем за первый. Найти темп инфляции за каждый период.
Решение. Используя формулу вычисления инфляции за два периода,
Слайд 51
Описание слайда:
Решение задачи 43.Задача 44
получим ; ;
или 13,46%;
Задача 44. Темп инфляции за период равен 0,4. Темп инфляции за первый период в 1,173 раза меньше, чем за второй. Найти темп инфляции за каждый период.
Решение. Используя формулу вычисления инфляции за два периода, получим
; ;
= 0,0992 или 9,92%.
Слайд 52
Описание слайда:
Задача 45
Прогнозируется среднемесячный темп инфляции 3%. Найти квартальный, полугодовой и годовой темп инфляции.
Решение. а) квартальный темп инфляции
равен или 12,55%.
б) полугодовой темп инфляции равен
или 19,41%.
в) годовой темп инфляции равен
или 42,58%.
Слайд 53
Описание слайда:
Задача 46
Месячный темп инфляции составляет 3%. Найти индекс цен и темп инфляции за год, определить наращенную сумму за год, если на сумму 200000 руб. в течение года начислялась простая (сложная) процентная ставка 15% годовых (К=360) , и определить ставку, при которой наращение равно потерям из-за инфляции.
Решение. Темп инфляции за год равен
или 42,58%, индекс цен 1,42
Слайд 54
Описание слайда:
Решение задачи 46
Наращенная сумма равна 200000∙1,15 = 230000 .
В случае сложных процентов месячная ставка равна или 1,17%. Годовая ставка, при которой потери из-за инфляции равны наращению составит 42,58%.
Слайд 55
Описание слайда:
Задача 47
Темп инфляции за период равен 1,2. Темпы инфляции за периоды
соответственно, составляют арифметическую прогрессию с разностью 0,1. Найти темп инфляции за каждый период.
Решение. Используя формулу вычисления инфляции за три периода, получим
;
Слайд 56
Описание слайда:
Решение задачи 47.Задача 48
; f(0,2) = -0,016 < 0; f(0,21) = 0,03 > 0. Следовательно, с точностью до 0,05, ; ; .
Задача 48. Прогнозируется среднемесячный темп инфляции 1%. Годовая номинальная ставка 15%. Найти эффективную реальную ставку, если начисление происходит 6 раз в году.
Решение. Годовая ставка инфляции
;
Слайд 57
Описание слайда:
Решение задачи 48. Задача 49
реальная годовая процентная ставка
= = 0,0206; эффективная годовая ставка или 2,08%.
Задача 49. Пусть темп инфляции за месяц равен 2%. Найти темп инфляции за год при условии постоянства темпа инфляции в течение года.
Решение. Годовой темп инфляции равен
или 26,82%.
Слайд 58
Описание слайда:
Задачи 50, 51
Пусть темп инфляции за год равен . Найти темп инфляции за квартал при условии его постоянства.
Решение. Темп инфляции за квартал равен
или 4,6%.
Задача 51. Какую ставку должен установить банк, чтобы при инфляции 8% годовых он мог бы иметь 10% доходность?
Решение. Воспользуемся формулой Фишера
; ; ; или 18,8%.
Слайд 59
Описание слайда:
Задача 52
Найти реальный доход вкладчика, если на депозит положено 200000 у.е. на 4 года под 15% годовых с ежемесячным начислением процентов при квартальной инфляции, которая составляет в среднем за данный период 3%.
Решение. Найдём годовой темп инфляции
. Вычислим реальный
процент по формуле Фишера
Слайд 60
Описание слайда:
Решение задачи 52. Задача 53
Реальный доход равен
Задача 53. При какой годовой процентной ставке сумма увеличится в 3 раза за 10 лет, если проценты начисляются поквартально?
Решение. Найдём процентную ставку , исходя из уравнения
Слайд 61
Описание слайда:
Решение задачи 53. Задача 54
Откуда ; ; или 11,14%.
Задача 54. Найти период времени , за который сумма, положенная на депозит под 13% годовых по схеме сложных процентов, возрастет в 4 раза.
Решение. Используем формулу наращения
как уравнение относительно n.
; ; .
Слайд 62
Описание слайда:
Задача 55
Компания имеет на депозите в банке 100000 руб. Депозитная ставка банка составляет 18% годовых. Предлагается объединить оборотные средства в совместном предприятии, которое прогнозирует утроение капитала через 8 лет. Провести сравнение вариантов вложения капитала.
Решение Найдём наращенную сумму в банке
Слайд 63
Описание слайда:
Решение задачи 55. Задача 56
за 8 лет. . Следовательно, оставить деньги на депозите в банке выгоднее.
Задача 56. При какой годовой сложной процентной ставке сумма удвоится за 7 лет, если проценты начисляются ежеквартально?
Решение. Используем правило семидесяти
в качестве уравнения. ; = 10%.
Слайд 64
Описание слайда:
Задача 57.
При какой годовой сложной процентной ставке сумма утроится за 6 лет, если проценты начисляются ежемесячно? ежеквартально?
Решение. Используем формулу наращения
как уравнение относительно . При ежемесячном начислении процентов
; или 18,45%. При ежеквартальном –
или 18,73%.
Слайд 65
Описание слайда:
Задача 58
Задача 58. За сколько лет при ставке 10% годовых вклад вырастет в 4 раза в схеме простых процентов?
Решение. Используем формулу наращения
как уравнение относительно n.
; ; .
Задача 59. За сколько лет удвоится капитал в схеме простых процентов при ставке 18% годовых?
Слайд 66
Описание слайда:
Задачи 59, 60, 61
Воспользуемся правилом «ста» .
Задача 60. За сколько лет удвоится капитал в схеме сложных процентов при ставке 18% годовых?
Решение. Воспользуемся правилом семидесяти .
Задача 61. Три платежа: 15000, 26000 и 45000 руб., произведенные в начале третьего, начале четвертого периодов и в
Слайд 67
Описание слайда:
Задачи 61, 62
конце пятого, соответственно, заменить платежом 90000 руб. Годовая ставка 15%.
Решение. Найдем срок платежа n исходя из уравнения эквивалентности
; ;
Задача 62. Три платежа: 13000, 25000 и 35000 руб., произведенные в начале
Слайд 68
Описание слайда:
Задача 62
третьего, начале четвертого периодов и в конце пятого, соответственно, заменить двумя платежами в конце шестого и седьмого периодов. При этом первый платеж в три раза больше второго. Годовая ставка сложных процентов равна 11%.
Решение. Обозначим второй из искомых платежей через S, тогда первый будет равен 3S. Найдем S, исходя из уравнения эквивалентности ; ;
Слайд 69
Описание слайда:
Решение задачи 62. Задача 63
Первый платёж равен , второй – .
Задача 63. Два платежа: 13000 и 35000 руб. произведенные в начале четвертого и в конце пятого периодов, соответственно, заменить
Слайд 70
Описание слайда:
Задача 63
двумя платежами в конце шестого и восьмого периодов. При этом первый платеж на 20% больше второго. Годовая ставка сложных процентов равна 9%.
Решение. Обозначим второй из искомых платежей через S, тогда первый будет равен 1,2S. Найдем S, исходя из уравнения эквивалентности ;
;
Слайд 71
Описание слайда:
Решение задачи 63. Задача 64
Первый платёж равен , второй –
.
Задача 64. Один платеж 43000 руб. в начале третьего периода заменить тремя равными платежами, произведенными в начале первого и в конце четвертого и седьмого периодов, соответственно. Годовая ставка простых процентов равна 17%.
Слайд 72
Описание слайда:
Решение задачи 64. Задача 65
Обозначим искомый платёж через S. Найдем S, исходя из уравнения эквивалентности ;
Задача 65. Резервный фонд создается в течение 18 лет. На поступающие в него средства начисляются сложные проценты по ставке 4,5% годовых.
Слайд 73
Описание слайда:
Задача 65
В течение первых 6 лет в конце каждого года в фонд вносили по 15000 у.е., в течение последующих 4 лет — по 18000 у.е. в конце года, а в последние 8 лет — по 22000 у.е. в конце года. Чему будет равна сумма фонда через 18 лет? Ответ привести с точностью до 0,01.
Решение. Сумма фонда S складывается из трёх наращенных сумм, каждая из которых
Слайд 74
Описание слайда:
Решение задачи 65
вычисляется по формуле . Причём, первая сумма лежит на депозите и наращивается в течение 12 лет, вторая – в течение 8 лет.
Задача 66. Семья планирует через 5 лет купить квартиру за 1900000 руб. и с этой целью ежемесячно на банковский депозит
Слайд 75
Описание слайда:
Задача 66
вносится определенная сумма. Найти ее, если годовая банковская ставка составляет 11% с ежемесячным начислением процентов.
Решение. Используем формулу Подставляя данные задачи, получим уравнение относительно годового взноса R.
. Откуда . Годовой платёж равен. Месячный
Месячный – 23893,94
Слайд 76
Описание слайда:
Задача 67
Какую сумму нужно положить в банк под 12% годовых мужчине 37 лет, чтобы по достижении им пенсионного возраста 60 лет в течение 15 лет в начале каждого месяца снимать по 10000 рублей, если проценты капитализируются: в конце года; в конце каждого полугодия; в конце каждого квартала; в конце каждого месяца?
Решение. Обозначим через A искомую сумму. Тогда к пенсионному возрасту эта
Слайд 77
Описание слайда:
Решение задачи 67
сумма нарастится до величины . Эта величина является приведённой суммой ренты (пенсии) и вычисляется по формуле
;
Проценты начисляются раз в год, k = 1.
Проценты начисляются раз в полгода, k = 2.
Слайд 78
Описание слайда:
Решение задачи 67. Задача 68
Проценты начисляются раз в квартал, k = 4.
Проценты начисляются раз в месяц, k = 12.
Задача 68. Сколько лет должна выплачиваться рента с годовым платежом 5000 руб., чтобы ее текущая (наращенная) стоимость превзошла величину 75000 руб. при процентной ставке 9% годовых?
Слайд 79
Описание слайда:
Решение задачи 68. Задача 69
Найдём наращенную величину(текущую стоимость) ренты и решим неравенство ;
; . Наименьшее число лет равно 10.
Задача 69. Фонд создается в течение 7 лет, взносы поступают в конце каждого полугодия равными суммами. На поступившие средства в конце года
Слайд 80
Описание слайда:
Задача 69
начисляется 12% годовых. На сколько процентов возрастет сумма фонда в конце седьмого года при переходе к непрерывной капитализации процентов?
Решение. При годовой капитализации сумма фонда составит величину
. При непрерывной капитализации сумма фонда составит величину
Слайд 81
Описание слайда:
Решение задачи 69. Задача 70
что в раза, или на 2,46%, больше, чем при годовой капитализации.
Задача 70. Фонд создается в течение 10 лет. Средства поступают в фонд в конце года равными суммами. На собранные средства в конце года начисляется 10% годовых. На сколько процентов возрастет наращенная сумма фонда при переходе к: а) взносам в конце каждого квартала; б) ежемесячному начислению процентов? Ответ привести с точностью до 0,01%.
Слайд 82
Описание слайда:
Решение задачи 70
При ежегодных взносах наращенная сумма равна . При ежеквартальных взносах наращенная сумма равна
, что в 1,03676 раза, или на 3,676%, больше, чем при годовых взносах. При ежемесячном начислении процентов наращенная сумма равна что в
раза, или на 2,29%, больше, чем при годовой капитализации.
Слайд 83
Описание слайда:
Задача 71
Какую сумму нужно положить в банк женщине 55 лет, чтобы в течение 18 лет в конце каждого года снимать по 3000 у.е., если на остаток вклада меньше 10000 у.е. начисляется 3% годовых, больше или равно 10000 у.е. — 4% годовых?
Решение. Найдём срок, в течение которого приведённая величина ренты меньше 10000. Воспользуемся формулой вычисления приведённой величины и
Слайд 84
Описание слайда:
Решение задачи 71
решим неравенство.
; ; ; ;
. Следовательно 3% будут начисляться последние 3 года, а 4% первые 15 лет. Искомый вклад равен сумме приведённой величины 15-летней ренты и дисконтированной приведенной величины 3-летней ренты и равен
Слайд 85
Описание слайда:
Задача 72
Фонд создается в течение 5 лет. Средства поступают в фонд в конце года по 50000 руб., на них начисляется 13% годовых. В каком случае сумма фонда станет больше: а) при переходе к ежемесячным взносам в конце каждого месяца; б) при переходе к ежедневной капитализации процентов? (К=365 дней).
Решение. Величина фонда (наращенная
Слайд 86
Описание слайда:
Решение задачи 72
сумма) при ежемесячных взносах равна
; при ежедневной капитализации процентов сумма фонда равна
В случае ежедневной капитализации процентов сумма меньше, чем в случае ежемесячных взносов.
Слайд 87
Описание слайда:
Задача 73
Для создания премиального фонда один раз в год производятся взносы в размере 15000 руб. На вносимые средства начисляются проценты под 12% годовых. Определить размер фонда через 7 лет в следующих случаях: а) поступление средств в конце года, ежеквартальное начисление процентов; б) поступление средств в конце квартала, начисление процентов 6 раз в году; в) ежемесячное поступление средств и ежеквартальное начисление процентов.
Слайд 88
Описание слайда:
Решение задачи 73
Воспользуемся формулой
а)
б)
в) .
Слайд 89
Описание слайда:
Задачи 74, 75
Задача 74. Формируется фонд на основе ежегодных отчислений в сумме 8000 у.е. с начислением на них сложных процентов по ставке 11%. Определить величину фонда через 10 лет.
Решение.
Задача 75. Определить размер вклада, который обеспечивает ежегодное (в конце года) получение денежной суммы в размере 1700 у.е. в конце года в течение 19 лет, если процентная ставка равна 11%.
Слайд 90
Описание слайда:
Решение задачи 75. Задача 76
= 1700 = 13326,8.
Задача 76. Дайте определение внутренней нормы доходности потока и найдите ее для потока .
Решение. Внутренняя норма доходности – это такая процентная ставка , при которой приведённая сумма потока равна нулю;
; ;
; ; ;
или 64,9%.
Слайд 91
Описание слайда:
Задача 77
Дайте определение внутренней нормы доходности потока и найдите ее для потока
.
Решение. Внутренняя норма доходности – это такая процентная ставка , при которой приведённая сумма потока равна нулю;
; ; ;
; ;
или 34,58%.
Слайд 92
Описание слайда:
Задача 78
Определить доходность инвестиций, выраженную в виде годовой ставки процента, если известно, что на 25000 руб. вложений доход составит 3000 руб. ежегодно в течение 17 лет.
Решение. Найдём искомый процент , исходя из формулы,
рассматриваемой в качестве уравнения относительно . ;
i = 13%.
Слайд 93
Описание слайда:
Задача 79
Сравните два потока по среднему сроку:
Решение. ;
Задача 80. Даны два потока: и . Какой из этих потоков является предпочтительнее? Почему?
Слайд 94
Описание слайда:
Решение задачи 80. Задача 81
Найдём современные величины обоих потоков. ; .
, так как ;
. Следовательно . Т. о. первый поток предпочтительнее.
Задача 81. Пусть поток платежей и процентная ставка составляет 10%. Найти приведенную стоимость и наращенную величину этого потока.
Слайд 95
Описание слайда:
Решение задачи 81. Задача 82
Приведённая стоимость равна.
. Наращенная величина равна .
Задача 82. Приведите поток
к моменту времени при ставке 8%.
Решение. Приведённая величина потока равна
Слайд 96
Описание слайда:
Задачи 83, 84
Приведите поток
к моменту времени при ставке 9%.
Решение. Приведённая величина потока равна
Задача 84. Найдите средний срок потока
.
Решение. Средний срок равен
Слайд 97
Описание слайда:
Решение задачи 84. Задача 85
Задача 85. На счет в банке помещено 160000 руб. За первые 5 лет и 6 месяцев процентная ставка равнялась 10%, а в следующие 7 лет и 4 месяца — 8%, капитализация полугодовая. Чему будет равна наращенная величина вклада через 12 лет 10 месяцев.
Решение.
Слайд 98
Описание слайда:
Задача 86
На счет в банке помещено 25000 руб., а через 5 лет сняли 20000 руб. Чему будет равна наращенная величина вклада через 12 лет (со дня помещения), если процентная ставка равна 11%, а капитализация полугодовая.
Решение. Через 5 лет сумма на банковском счете оказалась равной . Ещё через 7 лет сумма нарастится до величины
Слайд 99
Описание слайда:
Задача 87
Банк предлагает вкладчикам на двухлетний срок два варианта начисления процентов: 1) в первый год 2,5% ежеквартально, во второй год по 2% ежеквартально; 2) в первое полугодие по 3,5% ежеквартально, а в каждом последующем полугодии ежеквартальная ставка убывает на 0,5%. Какой вклад выгоднее.
Решение. 1) Наращенная сумма равна
Слайд 100
Описание слайда:
Решение задачи 87. Задача 88
2) Наращенная сумма равна
.
Второй вариант выгоднее.
Задача 89. Контракт предусматривает следующий порядок начисления сложных процентов: первый год — 11%, в каждом последующем полугодии ставка повышается на 1%. Определить множитель наращения за 2,5 года.
Слайд 101
Описание слайда:
Решение задачи 88. Задача 89
Множитель наращения является произведением четырёх множителей и равен .
Задача 89. Банк объявил следующие условия выдачи ссуды на один год: за первый квартал ссудный процент 30%; за второй квартал — 35%; за третий — 37%; за четвертый квартал — 40%. Определить сумму к возврату в банк, если ссуда составляет 200000 руб.
Слайд 102
Описание слайда:
Решение задачи 89. Задача 90
Сумма к возврату равна S = 200000∙(1 + 0,3) ∙(1 + 0,35) ∙(1 + 0,37) ∙(1 + 0,4) =673218.
Задача 90. Банк объявил следующие условия выдачи ссуды на один год: за первый квартал ссудный процент 30%; за второй квартал — 35%; за третий — 37%; за четвертый квартал — 40%. Определить сумму к возврату в банк, если ссуда составляет 200000 руб.
Слайд 103
Описание слайда:
Решение задачи 90. Задача 91
Сумма к возврату равна S = 200000∙(1 + 0,3) ∙(1 + 0,35) ∙(1 + 0,37) ∙(1 + 0,4) =673218.
Задача 91. Найти простую процентную ставку , эквивалентную сложной ставке для временного интервала в 6 лет при ежеквартальном начислении процентов.
Решение. Приравняем множители наращения и выразим ставку простых процентов. ; ;
Слайд 104
Описание слайда:
Задача 92
Найти простую процентную ставку , эквивалентную сложной ставке в 8% для временного интервала в 10 лет при ежемесячном начислении процентов.
Решение. Найдём ставку , исходя из равенства множителей наращения
; или 12,2%.
Слайд 105
Описание слайда:
Задачи 93, 94
Найти простую процентную ставку , эквивалентную непрерывной ставке 9%.
Решение. Найдём ставку , исходя из равенства множителей наращения
;
Задача 94. Найти сложную процентную ставку , эквивалентную непрерывной ставке 9%.
Слайд 106
Описание слайда:
Решение задачи 94. Задача 95.
Найдём ставку , исходя из равенства множителей наращения ;
или 9,42%.
Задача 95. Найти непрерывную процентную ставку , эквивалентную сложной ставке 5%.
Решение. Найдём ставку , исходя из равенства множителей наращения
; или 4,88%.
Слайд 107
Описание слайда:
Задачи 96, 97
Инвестор намерен положить некоторую сумму под 14% годовых с целью накопления через три года 1500000 руб. Определить сумму вклада.
Решение. Найдём искомую сумму исходя из уравнения ; .
Задача 97. Рыночная цена 12-ти процентной облигации номиналом 1000 руб. за два года до погашения равна 1200 руб.
Слайд 108
Описание слайда:
Задача 97.
Найти текущую стоимость облигации при процентной ставке: а) 10%, б) 14%, в) 12% и её курс.
Решение. Найдём курс или 120%. Текущая стоимость P вычисляется по формуле и равна следующим величинам:
а) ;
б) ;
Слайд 109
Описание слайда:
Задачи 97, 98
в) текущая стоимость P равна номинальной стоимости N и равна 1000, так как купонная и номинальная ставки равны.
Задача 98. Найти текущую стоимость облигации номинальной стоимостью 1000 руб., сроком погашения 5 лет и ежегодными выплатами по купонной ставке 15%, если годовая процентная ставка составляет 20%.
Слайд 110
Описание слайда:
Решение задачи 98. Задача 99.
Текущая стоимость P вычисляется по формуле и равна
.
Задача 99. Одна из двух бумаг портфеля является безрисковой. Рисковая бумага имеет параметры (0,4; 0,7), доходность безрисковой бумаги равна 0,31. Найти портфель и его доходность, если его риск равен 0,55.
Слайд 111
Описание слайда:
Решение задачи 99
Обозначим через долю рисковой бумаги, а через долю безрисковой бумаги, через
и доходность и риск рисковой бумаги. Риск портфеля вычисляется по формуле
. Следовательно ;
; . Доходность портфеля равна
Задача 100. Найдите изменение текущей рыночной стоимости облигации со сроком
Слайд 112
Описание слайда:
Задача 100
обращения n = 7 лет, номинальной стоимостью N = 50000, купонной ставкой с = 8% и доходностью к погашению ρ =10% при увеличении и уменьшении доходности к погашению на 2%.
Решение. Текущая рыночная стоимость облигации вычисляется по формуле
. При ставке доходности к погашению ρ = 10% рыночная стоимость
Слайд 113
Описание слайда:
Задачи 100, 101
равна ; при ставке 12% стоимость
; при ставке 8% стоимость .
Задача 101. Рыночная цена 20-ти процентной облигации номиналом 3500 руб. за два года до погашения равна 4300 руб. найти текущую стоимость облигации при процентной ставке: а) 14%, б) 20%, в) 23% и её курс.
Слайд 114
Описание слайда:
Решение задачи 101
Курс облигации равен или 122,86%. Текущую стоимость найдём по формуле
Слайд 115
Описание слайда:
Задачи 102, 103
Найти срок ренты постнумерандо, если известны .
Решение. Найдём срок ренты n, исходя из формулы вычисления наращенной суммы
; ; ;
Задача 103. Найти рентный платеж ренты постнумерандо, если известны
4
; ; ;
Слайд 116
Описание слайда:
Решение задачи 103. Задача 104
Найдём рентный платёж R, исходя из формулы вычисления приведённой величины A. ;
.
Задача 104. Семья планирует через 5 лет купить машину за 50000 у.е. С этой целью ежемесячно на банковский депозит вносится определенная сумма в у.е. Найти этот ежемесячный платеж, если годовая
з
Слайд 117
Описание слайда:
Задачи 104, 105
банковская ставка составляет 13% с ежемесячным начислением процентов.
Решение. . .
Месячный взнос равен R/12 = 492,3.
Задача 105. Найти размер вклада, обеспечивающего получение в конце каждого года 2000 руб. бесконечно долго при сложной ставке 14% годовых.
Решение.
задача
Слайд 118
Описание слайда:
Задача 106
Во сколько раз больше будет наращенная сумма в конце n-ого периода при ежепериодном (в конце периода) платеже R, чем при разовом платеже в начальный момент времени?
Решение. ; ;
Задача 107. Для бессрочной (вечной) ренты определить, что больше увеличит приведенную стоимость этой ренты,
Слайд 119
Описание слайда:
Задачи 106, 107
увеличение рентного платежа на 3% или уменьшение процентной ставки на 3%?
Решение. ; ; Увеличение процентной ставки приведёт к большему увеличению приведенной стоимости ренты.
Задача 107. Фонд создается в течение 12 лет с ежегодными взносами 120000 у.е. в конце года. На поступившие средства
Слайд 120
Описание слайда:
Задача 107
начисляется 4% годовых, если сумма не превышает 250000 у.е. и 4,5% годовых, если сумма превышает 250000 у.е. Чему будет равна величина фонда через 12 лет?
Решение. ; ;
; ;
Слайд 121
Описание слайда:
Задача 108
Сколько нужно вносить ежегодно на счет в банке под 5,5% годовых, чтобы через 14 лет накопить 90000 у.е., если: а) взносы в конце каждого квартала; б) взносы в конце каждого месяца?
Решение. Воспользуемся формулой
. В случае а) p = 4, k = 1, i = 0,055, n = 14, S = 90000. Следовательно
Слайд 122
Описание слайда:
Задачи 108, 109
. В случае б) p = 12;
Задача 109. За сколько лет можно накопить 150000 у.е., если в конце каждого квартала на счет вносится 10000 у.е. и на данные средства начисляются проценты в конце каждого полугодия по ставке 6% годовых? На сколько нужно увеличить годовые выплаты, чтобы срок уменьшился на полгода?
Слайд 123
Описание слайда:
Решение задачи 109. Задача 110
Воспользуемся формулой
где S = 150000; p = 4; i= 0,06; k = 2; R/4 = 10000; R =40000; Найти n. Имеем
Задача 110. Фонд создается в течение 10 лет, взносы поступают в конце каждого квартала равными суммами. На поступившие средства в конце года начисляется 7% годовых.
Слайд 124
Описание слайда:
Решение задачи 109
На сколько процентов возрастет сумма фонда в конце 10-го года при переходе к непрерывной капитализации процентов?
Решение. Найдём наращенную сумму при ежегодной капитализации
. Найдём наращенную сумму при непрерывной капитализации
. Искомый процент равен .
Слайд 125
Описание слайда:
Задача 110
Вычислить приведенную и наращенную величины непрерывной 7-летней ренты с непрерывным начислением процентов с рентным платежом 300 при ставке 15% годовых.
Решение. Приведенная величина равна
. Наращенная сумма равна
Слайд 126
Описание слайда:
Задача 111
Приведенная величина 12-летней ренты пренумерандо с непрерывным начислением процентов, процентной ставкой 5% равна 27000 руб. Найти наращенную сумму.
Решение. Воспользуемся формулой, связывающей наращенную величину с приведённой суммой
Слайд 127
Описание слайда:
Задача 112
Приведенная величина 7-летней ренты пренумерандо с ежемесячным начислением процентов, процентной ставкой 7,5%, равна 100000 руб. Найти наращенную сумму.
Решение. Наращенная сумма равна .
Слайд 128
Описание слайда:
Задача 113
Наращенная сумма 5-летней ренты постнумерандо с ежеквартальным начислением процентов, процентной ставкой 4,25% равна 50000 руб. Найти приведенную величину.
Решение. Найдём приведённую величину по формуле
Слайд 129
Описание слайда:
Задача 114
Во сколько раз увеличится приведенная величина ренты постнумерандо, если платежи платить в начале периода? Ставка равна 20%.
Решение. В 1 + i =1,2 раза.
Задача 115. Во сколько раз увеличится приведенная величина квартальной ренты постнумерандо, если платежи платить в начале периода? Ставка равна 30%.
Слайд 130
Описание слайда:
Решение задачи 115.
Приведённая величина ренты пренумерандо равна приведённой величине ренты постнумерандо, умноженной на множитель наращения за один малый период (квартал), т. е. на
. Следовательно приведённая величина ренты пренумерандо в 1,0678 раза больше приведённой величины ренты постнумерандо.
Слайд 131
Описание слайда:
Задача 116
Какова процентная ставка, если наращенная величина месячной ренты постнумерандо увеличится в 1,0234 раза, если платежи платить в начале периода?
Решение. Величина ренты пренумерандо в
раза больше приведённой величины ренты постнумерандо. Поэтому ;
или 31,99%.
Слайд 132
Описание слайда:
Задача 117
Какова процентная ставка, если приведенная величина ежедневной ренты постнумерандо увеличится в 1, 000687 раз, если платежи платить в начале периода (К=360)?
Решение. Величина ренты пренумерандо в
раза больше приведённой величины ренты постнумерандо. Поэтому, ;
или 28,05%.
Слайд 133
Описание слайда:
Задача 118
Заменить ренту с параметрами
рентой с параметрами .
Решение. Используем уравнение эквивалентности (равенство приведённых величин двух рент) .
; ;
;
Слайд 134
Описание слайда:
Задача 119
Замените годовую ренту параметрами
, на p-срочную (месячную) ренту .
Решение. Используем уравнение эквивалентности (равенство приведённых величин двух рент). ;
.
Слайд 135
Описание слайда:
Задача 120
Замените две ренты постнумерандо с параметрами и
разовым платежом в момент времени ,
И процентной ставкой
Решение. Используем уравнение эквивалентности (равенство приведённых величин двух рент)
Слайд 136
Описание слайда:
Задача 121
Консолидируйте три ренты постнумерандо с параметрами
4-летней рентой постнумерандо с .
Решение. Воспользуемся равенством суммы приведённых величин трёх данных рент и приведённой величины искомой ренты
Слайд 137
Описание слайда:
Задачи 121, 122
Задача 122. Пусть доходность актива за месяц равна 2%. Найти доходность актива за год при условии постоянства месячной доходности в течение года.
Слайд 138
Описание слайда:
Решение задачи 122. Задача 123
Доходность актива за год равна
или 26,28%.
Задача 123. Замените единовременный платеж 345000 руб. в момент времени
-срочной рентой постнумерандо с параметрами
Решение. Приравняем современные величины данного платежа и искомой ренты
Слайд 139
Описание слайда:
Задачи 123, 124, 125
Задача 124. Доходность актива за год равна 24%. Найти доходность актива за квартал при условии ее постоянства.
Решение. Квартальная ставка равна
или 5,53%.
Задача 125. Замените единовременный платеж 600000 руб. в момент времени и процентной ставкой 8% -срочной рентой
Слайд 140
Описание слайда:
Задача 125
постнумерандо с параметрами
Решение. Приравняем современные величины данного платежа и искомой ренты
Слайд 141
Описание слайда:
Задачи 126, 127
Пусть доходности за два последовательных периода времени равны 20% и 30% соответственно. Найти доходность за период .
Решение. Годовая доходность равна
или 56%.
Задача 127. По вине пенсионного фонда семье в течение 3 лет не доплачивали 625 руб. ежемесячно. Какую сумму должен
Слайд 142
Описание слайда:
Задачи 127, 128
должен выплатить фонд вместе с процентами (10% годовых)?
Решение. Сумма выплаты равна
Задача 128. Доходность актива за период
равна 0,75. Доходности актива
за периоды соответственно составляют геометрическую прогрессию со знаменателем 1,2. Найти доходность актива за каждый период.
Слайд 143
Описание слайда:
Решение задачи 128
Доходности активов за периоды равны
. Тогда
Так как значения функции f имеют разные знаки в точках 0,168 и 0,17, то с точностью до 0,001 (0,1%) искомое значение доходности
Иногда в задачах сказано, что кредит гасится, например, тремя платежами, а это значит, что (_<3>=0).
Проведя аналогичные рассуждения для (N) лет, можно вывести следующие формулы:
Источник
Как научить школьника решать любую банковскую задачу
Антонина Белова
В части с развернутым ответом в ЕГЭ по профильной математике есть уникальный номер, к которому школьник почти готов сразу после освоения материала для первых 12-ти заданий. Речь об экономической задаче под номером 17 в ЕГЭ по математике. Конечно, поготовиться придется, но, если повезет с прототипом, баллы можно урвать почти даром!
Как научить школьника решать экономическую (банковскую) задачу в ЕГЭ по математике
Прототипы для 17-го номера делятся на три большие группы:
- банковские задачи,
- на ценные бумаги,
- задачи на оптимальный выбор.
В этой статье мы расскажем, как научить ученика структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение. Расскажем, на что обратить внимание ученика, чтобы школьник не потерял баллы из-за неверного оформления.
Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.
- Как работает процент по кредиту?
- На какую сумму начисляется?
- Из каких частей состоит платеж?
- Как уменьшается долг?
На все эти вопросы вам придется ответить. Это отличная возможность показать пользу уроков математики, ведь 17-ый номер — едва ли не самая прикладная задача за весь школьный курс!
Например, можно рассказать о том, какие бывают образовательные кредиты. Вы в курсе, что их дают с 14 лет, а платеж первые годы может быть ничтожным? Школьник об этом точно не знает.
С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике
Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность рассказать школьнику что-то из реальности! Если у вас есть опыт с кредитованием, самое время им поделиться. Если нет, то воспользуйтесь нашим:
- Например, расскажите, что клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Ваши ученики знают, как работает страховка?
- Расскажите о механизме аннуитетного платежа: как часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
- Например, по нашему опыту, в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг.
Хорошая новость в том, что в экзаменационных задачах подобной вакханалии не бывает. Долг и проценты или гасятся равномерно, или по заранее известному алгоритму, достаточно просто внимательно прочитать условие.
Еще одно частое упрощение в ЕГЭ — процент там обычно не годовой, а ежемесячный! То есть своим платежом заемщик гасит набежавший за этот месяц процент и уменьшает долг на заданную величину. Удобно.
Мы предлагаем научить школьника упорядочивать данные банковской задачи в ЕГЭ по математике с помощью таблицы. Табличка — не единственный способ решить 17-ый номер, кто-то использует последовательности, кто-то — считает прикладным методом как заправский бухгалтер. Однако наш метод универсален, а значит вы дадите школьнику один алгоритм на все типы банковских задач. Согласитесь, работать с одним алгоритмом проще, чем подбирать разные по ситуации.
Тип 1. Равные платежи
Особенность этого типа заданий в том, что заемщик всегда вносит одинаковые суммы.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.
Очевидно, что эта схема должна оказаться у школьника в тетради. Ведь вы же знаете: того, чего нет в тетради, и на уроке-то не было!
Заполняем всю табличку. Учитываем обе ситуации из условия. Для наглядности каждую выделим жирной рамкой.
Теперь остался еще один непростой шаг — перейти от структурированных данных к математической модели. Дайте ученику возможность увидеть, что уже почти составил ее.
Мы получили два уравнения, которые подсветили в табличке оранжевым. Объединим их в систему и решим!
Напомните выпускнику о культуре вычислений! Порой эти задачи составлены так, что неудачная последовательность действий сделает их нерешаемыми без калькулятора. Потому не надо спешить делать первое попавшееся действие, пусть школьник тренируется думать на пару ходов вперед.
Например, разделим одно уравнение на другое, ведь так мы избавимся от одной неизвестной S:
Наше решение не зависит от суммы кредита, S сокращается.
По сути, мы получили уравнение с одной неизвестной, ведь платежи a и b знаем из условия. Выразим k:
Пожалуй, все, проще уже некуда. Подставляем значения!
Тут можно обратить внимание ученика на то, как составители экзамена на самом деле заботятся о нем! Ведь будь задачка хоть чуть-чуть другой, посчитать без калькулятора было бы невозможно.
Вспоминаем, что k=1+r/100, а найти нам надо r.
Не забудьте после решения расставить акценты в задаче:
Чтобы решить задачу и получить 3 балла, мы:
— Воспользовались простым алгоритмом упорядочивания данных,
— Составили математическую модель,
— Нашли удобный способ решить ее, ВСЕ!
Это и есть алгоритм решения банковской задачи.
Тип 2. Равномерно убывающий долг
В прошлой задаче заемщик платил одинаковую сумму каждый месяц. Тут ему нужно уменьшать долг на одну и ту же величину. То есть за месяц пользования деньгами банк начислил на них процент, клиент теперь должен чуть больше. Своим платежом он оплатит банку проценты, чтобы заем стал таким, как ДО их начисления. А сверху внесет сумму, которая как раз и пойдет на то самое РАВНОМЕРНОЕ уменьшение долга.
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся.)
Тут главный элемент в задаче — равномерно убывающий долг. Если мы взяли сумму S на 39 месяцев, и каждый месяц долг должен быть меньше на одинаковую величину, то что это за величина? Пусть правильный ответ 1/39 S даст ученик.
Проиллюстрируйте школьнику, как здорово работает наш алгоритм. Пусть выпускник проговаривает пункты вслух, а вы их выполняйте. Следите, чтобы каждый шаг подопечный фиксировал в тетради:
Продолжаем заполнять табличку. Пусть дальше пробует выпускник, ведь пока сам не попробуешь, не научишься:
Осталось увязать добытую информацию в уравнение или неравенство. Обратите внимание подопечного на то, что ненужных подробностей в задачах ЕГЭ не бывает! Единственная информация в задаче, которую мы до сих пор не использовали — общая сумма выплат. По условию она на 20% больше суммы кредита, то есть равна 1,2S:
Приведем подобные, вынесем общий множитель за скобку:
Решение в итоге снова не зависит от того, какую сумму взяли в долг. Разделим обе части на S и упростим выражение:
И снова все по нашему алгоритму, ничего нового, кроме него, мы не используем! Не забудьте излучать восторг, иначе школьник не проникнется мощью вашего метода решения.
Тип 3. Долг, убывающий согласно табличке
Задача похожа на прошлую. Разница лишь в том, что кроме процентов нам каждый месяц придется гасить не равную долю долга, а долю согласно таблице.
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг(в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.
Протестируем нашу универсальную табличку в третий раз, доверьте это непростое занятие школьнику. Пусть процессом командует он! По ответам будет ясно, ловит ли он суть.
Отличие от прошлого типа будет лишь в том, что в третий столбец мы будем записывать не равномерно убывающий долг, а перенесем остаток долга из таблицы условия. Чтобы не таскать по решению нули, считать будем в миллионах:
Чтобы долг убывал согласно табличке, нам снова каждый раз придется гасить набежавшие проценты и первые 5 месяцев добавлять сверху 0,1 млн. После останется погасить весь остаток.
Акцентируйте внимание на механизме погашения, для школьника он не всегда очевиден.
«По условию нам снова дана общая сумма выплат, значит достаточно просуммировать оранжевый столбец, и уравнение готово», — вероятно, подумает школьник. Подловите его! Уравнение в этой задаче — прямой путь потерять балл! Сумма выплат должна быть БОЛЬШЕ 1,2 млн. Отразим это в модели с помощью неравенства:
Подопечный должен быть уверен в каждом символе в бланке ответа. Даже не пригодившиеся промежуточные вычисления с ошибкой приведут к катастрофе.
Приведем подобные и вынесем общие множители за скобку:
Последний шаг – не забыть, что по условию процент должен быть целым и округлить в верную сторону.
Правильная математическая модель — это суперважно! К ней проверяющие обязательно придерутся.
Тип 4. Погашение кредита в два этапа.
По сути, это та же прошлая задача, но месяцев больше
В 2017-2018 учебном году составителей экзамена посетило вдохновение, на свет родился вот этот тип банковских задач. Школьники были в шоке, и от страха завалили 17-ый номер. Хотя всего-то нужно было догадаться воспользоваться знаниями об арифметической прогрессии и достать из условия одно немного неочевидное дано!
15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?
И снова пусть по возможности командует школьник. По крайней мере он уже точно в курсе, что происходит первые 13 месяцев.
Последовательно начисляем процент на остаток долга – считаем выплату – фиксируем остаток долга после выплаты. Сумму кредита возьмем за S.
Научите школьника не спешить с вычислениями. Например, вместо того чтобы написать S-600, мы пишем S-50*12, потому что так удобнее: нам сразу ясно, что речь идет о двенадцатом месяце. Да и потом вычисления будут проще, если мы оставим маленькие числа.
Осталось составить уравнение, и модель готова. В задаче нам снова дали сумму всех выплат:
Как обычно, сгруппируем отдельно слагаемые с r/100, отдельно слагаемые без них:
Вот именно последняя группировка всех платежей в счет долга и оказалась неочевидной. Без нее в задаче остается одна лишняя неизвестная величина, которая рушит все решение.
Осталось привести уравнение к решаемому виду. Для этого надо просуммировать то, что получилось в скобках. Если внимательно приглядеться, то видно, что это сумма арифметической прогрессии:
Посчитаем эту сумму:
Подставляем выражение для суммы в уравнение, заметим, что по условию r=2:
Мы сокращали дробь, пока это было возможно, и в итоге довольно просто получили ответ даже без калькулятора. Ваш подопечный должен научиться также!
Ответ: 700 тысяч.
Зачем использовать формулу суммы прогрессии, если можно посчитать вручную? Все верно, можно. Но это только в данном случае кредит взяли всего на 13 месяцев. А бывают прототипы, когда срок – 21 и больше месяцев. В какой-то момент считать вручную станет совсем долго и неудобно, потому воспользоваться формулой суммы – более универсальный метод.
Чем закончить разбор экономической (банковской) задачи № 17 в ЕГЭ по математике
Чтобы у ученика окончательно сложилась картинка занятия, пробегитесь еще раз по основным выводам:
- Повторите алгоритм заполнения таблицы и решения задачи (да, пятый раз);
- Повторите типы задач и механизм распределения платежа на проценты и долг;
- Напомните, как важно считать культурно и быть уверенным в каждой циферке в бланке;
- Проговорите, что математическая модель должна точно отражать условие задачи.
Как показывает практика, чем больше повторяешь, тем больше шансов, что в голове выпускника останется хоть что-то.
За что дают баллы?
Знание критериев оценивания экономической (банковской) задачи № 17 в ЕГЭ по математике поможетученику чувствовать себя увереннее, ведь выставление баллов — это не какая-то магия и не вредность экспертов. Все правила игры прописаны в нормативных документах.
17-ый номер стоит 3 балла. Чтобы узнать, как их присуждают, мы залезли в методические рекомендации для членов предметных комиссий.
Согласно пояснениям из документа, для получения одного балла мало просто обоснованно составить математическую модель по задаче, надо предложить правильный метод ее анализа.
Два балла получит школьник, который ошибся в вычислениях или не обосновал появление математической модели в решении. Например, согласно методическим рекомендациям, решение на 2 балла выглядит так:
А вот отсутствие промежуточных вычислений хоть и усложняет проверку, но баллы не снимает.
Идеально выполненная первая часть ЕГЭ по профильной математике принесет школьнику всего 62 тестовых балла. Добавим сюда пару ошибок по невнимательности, и останутся совсем крохи — баллов 50, не больше. Для поступления на бюджет мало, а значит необходимо планировать делать вторую часть! Чем раньше школьник это осознает, тем проще будет с ним работать. А банковская задача поможет получить дополнительные баллы с минимальными усилиями.
Однако кредиты – не единственный прототип 17-го номера, и в следующий раз мы расскажем, как научить школьника решать задачи на оптимальный выбор и ценные бумаги.
Источник
Предлагая клиенту «рассчитать кредит», сотрудник банка, как правило, подразумевает расчет максимально доступной заемщику суммы займа, а также расчет размера ежемесячного платежа и переплаты при помощи кредитного калькулятора. Многие банки также предоставляют заемщикам возможность рассчитать максимальную сумму займа и график платежей самостоятельно, воспользовавшись этим инструментом.
Чтобы рассчитать доступную пользователю сумму, вводится размер ежемесячного дохода потенциального заемщика или его семьи, а в некоторых случаях — отдельное поле, где указывается сумма расходов на содержание иждивенцев, погашение других займов и тому подобное. Иногда эти сервисы не учитывают доход заемщика и позволяют узнать только размер ежемесячного платежа и сумму переплаты. Рассчитать указанные параметры онлайн можно также при помощи размещенных в Интернете универсальных инструментов для сравнения и анализа банковских продуктов.Варианты расчетов:
- с онлайн заявкой
- с рефинансированием
- с выдачей наличными
- с досрочным погашением
Вопросы и ответы
💡 Как использовать кредитный калькулятор от Банки.ру?
Самая выгодная ставка на кредит без отказа на 22.03.2023 составляет 2.73%.
🧮 В каких банках доступен расчет кредита с помощью калькулятора?
На Банки.ру можно рассчитать кредит для большинства российских банков. Например, Сбербанк, ВТБ, Совкомбанк, Почта банк, Альфа Банк, Тинькофф и многие другие.
Формула расчета процентов по кредиту
Чтобы рассчитать проценты по кредиту вручную, необходимо воспользоваться следующей формулой:
Процент по кредиту = Остаток задолженности * (ставка % / 12 месяцев)
| 🔷 Минимальная ставка по кредиту: | 1.4% |
| 🔷 Максимальный срок кредита: | 30 лет |
| 🔷 Максимальная сумма кредита: | 100 000 000 ₽ |
| 🔷 Количество предложений: | 247 |
Задача: рассчитать сумму ежемесячных процентов по кредиту и составить проводки
Здравствуйте! Помогите, пожалуйста, с решением следующей задачи:
В начале отчетного года организацией получен в банке кредит на сумму 1 млн. руб. сроком на 3 года под 20% годовых для строительства цеха.
Цех введен в эксплуатацию в декабре этого же года. Проценты по кредиту выплачиваются в конце каждого месяца.
Задание: Рассчитать сумму ежемесячных процентов и определить сумму процентов, включенных в себестоимость цеха. Составить проводки, отражающие получение и возврат кредита, начисление и уплату процентов.
Итак, я решала следующим образом:
1 000 000 * 20% = 200 000; 1 000 000 + 200 000 = 1 200 000 руб. — сумма кредита с процентом.
1 200 000 : 36 месяцев = 33 333 — сумма кредита к уплате за месяц.
Проводки:
1. Получен кредит — Дт 51 Кт 67. Сумма: 1 000 000
2. Начислены проценты — Дт 91.2 Кт 67. Сумма: 200 000
3. Уплачен процент за месяц — Дт 67 Кт 51. Сумма: 33 333
4. Возврат кредита — Дт 67 Кт 51. Сумма: 1 200 000
Буду очень благодарна, если кто-нибудь уделит мне время. Прошу прощение за ошибки, если таковые имеются. В свое оправдание скажу, что преподаватель тему не объяснил, но задачу дать не забыл(
Наида Холод, здравствуйте.
«1 000 000 * 20% = 200 000»
«Рассчитать сумму ежемесячных процентов»
Вам нужно считать проценты ежемесячно.
1 000 000 х 20% = 200000,00 /365 х 31 день (если это январь) = 16986,30 руб.
и так далее…
«1 200 000 : 36 месяцев = 33 333 — сумма кредита к уплате за месяц.»
Насколько я понимаю, что про суммы именно кредита возвращаемаю ежемесячно в задаче нет условия.
Получите образец учетной политики и ведите бухучет в веб‑сервисе для небольших ООО и ИП
Здравствуйте
Цитата (Наида Холод):1. Получен кредит — Дт 51 Кт 67. Сумма: 1 000 000
Эта проводка верная.
Цитата (Наида Холод):2. Начислены проценты — Дт 91.2 Кт 67. Сумма: 200 000
Эта проводка верная, но сумма неверная. Вы начислили 20% от 1 млн., но не умножили на 3 года.
Цитата (Наида Холод):я решала следующим образом:
1 000 000 * 20% = 200 000; 1 000 000 + 200 000 = 1 200 000 руб. — сумма кредита с процентом.
1 200 000 : 36 месяцев = 33 333 — сумма кредита к уплате за месяц.
Неверный расчет. Не умножили как минимум на 3 года. В жизни конечно проценты считаются от суммы задолженности либо аннуитетными платежами.
Если упростить ситуацию для задачи, то проценты будут 1 000 000 х 20% х 3 года = 600 000= это только проценты
Для проводки Д (08) 91 К 67 нужно 600 000 / 36 месяцев = 16 666,67 (ежемесячная уплата процентов).
До ввода цеха в эксплуатацию проценты включаются в его стоимость, т.е. проводка Д 08 К 67 сумма 16 666,67 (ежемесячно до даты ввода цеха в эксплуатацию).
Следующие месяцы проценты начисляете проводкой Д 91 К 67
Цитата (Наида Холод):4. Возврат кредита — Дт 67 Кт 51. Сумма: 1 200 000
проводка верная, сумма — нет.
Кредитный калькулятор
Выберите способ расчета
По сумме кредита
По стоимости покупки
Первоначальный взнос
(80 000 ₽ в кредит)
Вид платежей
Равные
Уменьшаемые
Платеж в месяц
4 500 ₽
Срок выплат
36 мес.
Сумма выплат
55 811 ₽
Переплата
5 811 ₽
График платежей
| №, Месяц |
Сумма платежа Платеж |
Проценты + долг | Остаток долга |
|---|---|---|---|
| 1. 10.04.2019 |
61 811.94 3 000.00 + 58 811.94 |
3 000.00 + 58 811.94 | 241 188.06 |
| 1. 10.04.2019 |
61 811.94 3 000.00 + 58 811.94 |
3 000.00 + 58 811.94 | 241 188.06 |
Лучшие предложения
Тинькофф Платинум
| Кред. лимит | 700 000Р |
| Проц. ставка | От 12% |
| Без процентов | До 12 мес. |
| Стоимость | От 0 руб./год |
| Кэшбек | До 30% |
| Решение | 2 мин. |
Карта Kviku
| Кред. лимит | 100 000Р |
| Проц. ставка | От 10% |
| Без процентов | 50 дней |
| Стоимость | 0 руб. |
| Кэшбек | До 30% |
| Решение | 1 мин. |
Газпромбанк 180 дней
| Кред. лимит | 1 000 000Р |
| Проц. ставка | От 11,9% |
| Без процентов | 180 дней |
| Стоимость | От 0 руб. |
| Кэшбек | До 50% |
| Решение | 5 минут |
Альфа-Банк 365 дней без %
| Кред. лимит | 500 000Р |
| Проц. ставка | От 11,99% |
| Без процентов | До 365 дней |
| Стоимость | 0 руб. |
| Кэшбек | До 33% |
| Решение | 2 мин. |
Газпромбанк кредит
| Макс. сумма | 7 000 000Р |
| Ставка | От 4,4% |
| Срок кредита | До 5 лет |
| Мин. сумма | 100 000 руб. |
| Возраст | 20-70 лет |
| Решение | От 10 минут |
Альфа-Банк кредит
| Макс. сумма | 7 500 000Р |
| Ставка | От 4,5% |
| Срок кредита | 1-5 лет |
| Мин. сумма | 50 000 руб. |
| Возраст | От 21 года |
| Решение | 2 мин. |
Почта Банк кредит
| Макс. сумма | 5 000 000Р |
| Ставка | От 4,5% |
| Срок кредита | До 7 лет |
| Мин. сумма | 10 000 руб. |
| Возраст | От 18 лет |
| Решение | 1 мин. |
Тинькофф Кредит
| Макс. сумма | 2 000 000Р |
| Ставка | От 7,9% |
| Срок кредита | До 5 лет |
| Мин. сумма | 50 000 руб. |
| Возраст | 18-70 лет |
| Решение | 2 минуты |
Все Кредиты
Тинькофф Блэк
| Стоимость от | 0 Р |
| Кэшбек | 1-30% |
| % на остаток | До 6% |
| Снятие без % | До 500 000 руб. |
| Овердрафт | Есть |
| Доставка | 1-2 дня |
Альфа-Карта
| Стоимость от | 0Р |
| Кэшбек | 1-100% |
| % на остаток | До 9% |
| Снятие без % | До 50 000 р. |
| Овердрафт | Нет |
| Доставка | Банк/курьер |
МТС CASHBACK
| Стоимость от | 0 Р |
| Кэшбек | 1-25% |
| % на остаток | До 7% |
| Снятие без % | 100 000 ₽/мес. |
| Овердрафт | Нет |
| Доставка | 1 день |
Росбанк #МожноВСЁ
| Стоимость от | 0Р |
| Кэшбек | 1-5% |
| % на остаток | До 8,5% |
| Снятие без % | 150000 ₽/сут. |
| Овердрафт | Нет |
| Доставка | На дом |
Веб-займ (0% первый займ)
| Сумма займа | 30 000Р |
| Проц. ставка | От 0% |
| Срок займа | До 30 дней |
| Кред. история | Любая |
| Возраст | 18-90 лет |
| Решение | 5 мин. |
До зарплаты (0% первый займ)
| Сумма займа | 100 000Р |
| Проц. ставка | От 0% |
| Срок займа | До 365 дней |
| Кред. история | Любая |
| Возраст | От 18 лет |
| Решение | 7 мин. |
Займер (0% первый займ)
| Сумма займа | 30 000Р |
| Проц. ставка | От 0% |
| Срок займа | До 30 дней |
| Кред. история | Любая |
| Возраст | 18-75 лет |
| Решение | 2 мин. |
Манимен (0% первый займ)
| Сумма займа | 80 000Р |
| Проц. ставка | От 0% |
| Срок займа | До 126 дней |
| Кред. история | Любая |
| Возраст | 18-70 лет |
| Решение | 1 мин. |
СберВклад в Сбербанке
| Сумма от | 100 000Р |
| Проц. ставка | До 6,2% |
| Срок | До 3 лет |
| Макс. сумма | Любая |
| Пополнение | Возможно |
| Снятие | Нет |
Кредит Клаб
| Сумма от | 100 000Р |
| Проц. ставка | До 15% |
| Срок | До 2 лет |
| Макс. сумма | 40 млн |
| Пополнение | Да |
| Снятие | Да |
Вклад в Альфа-Банке
| Сумма от | 10 000Р |
| Проц. ставка | До 9,5% |
| Срок | До 3 лет |
| Макс. сумма | Любая |
| Пополнение | Нет |
| Снятие | Нет |
Вклад в Тинькофф Банке
| Сумма от | 50 000Р |
| Проц. ставка | До 8% |
| Срок | До 2 лет |
| Макс. сумма | 30 млн руб. |
| Пополнение | Возможно |
| Снятие | Возможно |
ВТБ рефинансирование кредитов
| Макс. сумма | 7 000 000Р |
| Ставка | От 4,4% |
| Срок кредита | До 7 лет |
| Мин. сумма | 30 000 руб. |
| Возраст | 23-75 лет |
| Решение | 2 минуты |
Тинькофф автокредит
| Макс. сумма | 3 000 000Р |
| Ставка | От 14,9% |
| Срок кредита | До 5 лет |
| Мин. сумма | 100 000 руб. |
| Возраст | От 18 лет |
| Решение | За 1 мин. |
Альфа-Банк автокредит
| Макс. сумма | 7 500 000Р |
| Ставка | От 4% |
| Срок кредита | До 5 лет |
| Мин. сумма | 50 000 ₽ |
| Возраст | От 21 года |
| Решение | 2 мин. |
Газпромбанк автокредит
| Макс. сумма | 7 000 000Р |
| Ставка | От 2,4% |
| Срок кредита | До 5 лет |
| Мин. сумма | 500 000 руб. |
| Возраст | 20-70 лет |
| Решение | За 5 минут |
Газпромбанк кредит на мотоцикл
| Макс. сумма | 7 000 000Р |
| Ставка | От 2,4% |
| Срок кредита | До 5 лет |
| Мин. сумма | 500 000 руб. |
| Возраст | 20-70 лет |
| Решение | За 5 минут |
Тинькофф РКО
| Обслуживание | 490Р |
| % на остаток | 3% |
| Пополнение | 0 руб. |
| Платеж | От 19 руб. |
| Перевод | 0 руб. |
| Овердрафт | До 1 млн. р. |
РКО в Модульбанке
| Обслуживание | 690Р |
| % на остаток | 4 |
| Пополнение | 0 руб. |
| Платеж | От 0 руб. |
| Перевод | 0 руб. |
| Овердрафт | Нет |
Локо-Банк РКО
| Обслуживание | 0Р |
| % на остаток | 8,75% |
| Пополнение | 0 руб. |
| Платеж | От 19 руб. |
| Перевод | 0 руб. |
| Овердрафт | нет |
Уралсиб РКО
| Обслуживание | 0Р |
| % на остаток | 3% |
| Пополнение | 0,25% |
| Платеж | От 0 руб. |
| Перевод | До 150 000 ₽ |
| Овердрафт | Индивидуально |
Семейная ипотека Росбанк Дом
| Макс. сумма | 12 000 000Р |
| Ставка | От 3.95% |
| Срок кредита | 3-35 лет |
| Первонач. взнос | От 15% |
| Возраст | 21-65 лет |
| Решение | 10 минут |
Ипотека Альфа-Банк Новостройки
| Макс. сумма | 70 000 000Р |
| Ставка | От 8% |
| Срок кредита | До 30 лет |
| Первонач. взнос | От 15% |
| Возраст | 21-70 лет |
| Решение | От 1 минуты |
Кредиты в городах
Наш банковский калькулятор сделает расчет кредита в один клик. Просто укажите параметры интересующего вас потреб. кредита и программа сделает предварительный расчет в автоматизированном режиме. Помесячный график выплат будет сформирован под формой и будет содержать таблицу платежей с разделением на основную сумму задолженности и процентов.
Банковский калькулятор для расчета потребительского кредита наличными
Перед оформлением потребительского кредита многих граждан интересуют условия, по которым происходит кредитование. Сколько мне придется платить в месяц? Сколько я переплачу за весь срок? Сколько составит процент переплаты по будущему денежному кредиту? Это распространенные вопросы, ответы на которые люди ищут в Интернете в 2019 году и будут искать в 2020, 2021 и последующих годах. Наши специалисты разработали универсальный кредитный калькулятор, работающий полностью онлайн, который поможет ответить на них.
Опишем подробно как самостоятельно правильно работать с данной программой расчета.
Что может посчитать этот калькулятор?
Правильно рассчитать кредит не требует наличия особых знаний. Наша программа создана таким образом, что пользоваться ей будет просто как среднестатистическим физическим лицам, так и пенсионерам. Предварительно вы можете задать 4 параметра в форме:
- Сумму денежного кредита (200000, 500000, 800000 или любую другую). Двигая ползунком максимальная сумма составит 15 000 000 рублей, однако вы можете вписать любое произвольное число.
- Срок кредитования, который также может быть абсолютно любым — год, 2 года, 3 года, 4 года, 5 лет, 7 лет, но ползунком задан в пределах 6-180 месяцев.
- Процентная ставка ссуды. В качестве минимального значения мы поставил 8.9%, а максимальным — 49.9%. Но вы также можете поставить ту цифру, которая удобна для вас — 15 годовых, 18 годовых, 16 годовых или 20 годовых.
- И последнее — тип платежей. Если вы планируете платить кредит равномерными платежами (аннуитетными), то выбираете вкладку «Равные». Если же хотите чтобы сумма ежемесячного платежа со временем становилась меньше, то ставьте активной вкладку «Уменьшаемые» (дифференцированные).
Настроив данные условия, вам остается только нажать на кнопку «Рассчитать». Математические формулы в онлайн-режиме моментально предоставят вам данные по следующим параметрам:
- Размер ежемесячного платежа, в рублях.
- Сумма первоначального кредита.
- Полная стоимость (первоначальная + проценты).
- Общая переплата (процентны в рублях).
- Соотношение переплаты, в процентах.
Обычно после предварительного расчета посетители рассказывают о калькуляторе в социальных сетях, а также ставят рейтинг. По нему другие люди смотрят насколько наша программа удобна и полезна в использовании. А отзывы помогают сформировать единое мнение о функциональности и удобности калькулятора.
Составление графика платежей или как рассчитать выплаты по кредиту
Для решения данного вопроса также не нужно иметь специализированные умения. После после получения первоначальных данных, под формой откроется таблица, в которой будет отражен примерный график платежей по будущему краткосрочному или долгосрочному кредиту. В ней будут представлены помесячно следующие данные:
- номер месяца;
- точная дата совершения платежа;
- размер ежемесячного платежа (основной долг вместе с процентами);
- размер основного долга в платеже;
- размер процентов в платеже;
- остаток по кредиту после выплаты платежки.
Под таблицей выплат будет итоговая строка, в которой аккумулируются полная стоимость и переплата по кредиту. Вы поймете сколько платить за кредит по выбранным условиям заимствования денежных средств. Представленных данных также будет достаточно для оценки предварительного досрочного погашения.
Подбор выгодного кредита наличными
После того как вы сами рассчитаете сумму долга, вам будет доступен блок с самыми популярными кредитными предложениями. Команда сайт brobank.ru постаралась собрать в одном месте продукты многих банков России. Удобное расположение информации поможет вам оставить заявки в несколько банковских учреждений и после получения одобрения взять деньги в любом отделении банка.
Надеемся, наш банковский калькулятор оказался полезным для вас!


 Скачать 6.55 Mb.
Скачать 6.55 Mb.