Выбери правильные варианты ответов.
1. Работа силы является физической величиной.
2. Единица измерения работы (СИ):
- (1) ккал (килокалория)
- (1) кДж
- (1) Дж
- (1) Вт
- (1) лошадиная сила
3. Если тело совершает перемещение по горизонтальной шероховатой поверхности, то работа силы реакции опоры .
4. Механическая работа, совершаемая механизмом за конечный промежуток времени, характеризует его
.
|
5. Какая физическая величина вычисляется через площадь под графиком функции (F(t))? Ответ: . |
Рис. (1). Изображение графика |
Элементарным
импульсом силы
называют векторную величину, равную
произведению вектора силы на элементарный
промежуток времени,
.
(3.17)
Полным
импульсом силы
(импульсом силы за конечный промежуток
времени) называют векторную величину
.
(3.18)
Элементарной
работой силы
называют
скалярную величину dA,
равную произведению силы на элементарное
перемещение точки ее приложения или
произведению проекции силы на направление
движения точки на ее элементарное
перемещение:
,
или
,
(3.19)
где
–
угол между направлением силы и направлением
перемещения.
Косинус
угла
определяет знаки работ различных сил.
Алгебраическая
сумма всех элементарных работ будет
представлять полную работу силы на
конечном перемещении точки ее приложения.
Работа
силы тяжести:
,
(3.20)
где
h
– вертикальное
перемещение точки приложения силы
тяжести Р.
Знак
«плюс»
ставится, если точка приложения силы
тяжести опускается, знак «минус»
– в противном
случае
Работа
силы упругости:
(3.21)
где
x0
и xn
– начальная и конечная координата
точки; С
– коэффициент жесткости.
Работа
силы трения:
.
(3.22)
Работа
момента пары сил, приложенных к
вращающемуся телу,
вокруг
оси Oz
(3.23)
3.6. Общие теоремы динамики точки и системы
3.6.1.
Теорема
о движении центра масс. Закон сохранения
движения центра масс
Если
на k-ю
материальную точку, принадлежащую
механической системе, действуют внешние
и внутренние силы, то,
суммируя по всем точкам системы
(3.24)
получим
выражение для теоремы о движении центра
масс
(3.25)
Теорема:
«Центр
масс системы движется как материальная
точка, масса которой равна массе всей
системы и к которой приложены все внешние
силы, действующие на систему».
В
проекциях на оси декартовой системы
координат выражение
(3.25)
запишем следующим образом:
;
;
(3.26)
Закон
сохранения движения центра масс:
«Если
геометрическая сумма внешних сил,
действующих на систему, равна нулю
,
то– скорость центра масс есть величина
постоянная по модулю и направлению».
Если
при тех же условиях в начальный момент
времени
,
то положение центра масс есть величина
постоянная
Если алгебраическая сумма проекций на
какую-либо из координатных осей (например,
Ох)
внешних сил, действующих на систему,
равна нулю, то проекция скорости центра
масс на соответствующую ось –
величина постоянная
;
.
Если
при тех же условиях в начальный момент
времени
,
то положение центра масс, определяемое
радиус-вектором, есть величина постояннаяЕсли проекция начальной скорости на
какую-либо из координатных осей (например,Ох)
,
то
соответствующая координата центра масс
системы
.
3.6.2.
Теорема
об изменении количества движения
системы. Закон сохранения количества
движения
[1]
Теорема:
«Производная
по времени от вектора количества движения
системы равна геометрической сумме
внешних сил, действующих на систему».
Изменив
последовательность дифференцирования
и суммирования в (3.24), получим
,
(3.27)
а
учитывая (3.4),
запишем выражение для теоремы об
изменении количества движения в
дифференциальной форме:
(3.28)
В
проекциях на оси декартовой системы
координат оно выглядит следующим
образом:
;
;
(3.29)
Закон
сохранения количества движения:
«Если
геометрическая сумма всех внешних сил,
действующих на систему, равна нулю, то
вектор количества движения системы
будет постоянен по модулю и направлению»
=
0;
.
Если
алгебраическая сумма проекций на
какую-либо из координатных осей (например,
Oх)
внешних сил, действующих на систему,
равна нулю, то проекция количества
движения системы на соответствующую
ось –
величина постоянная
;
.
Интегрируя
(3.28) в пределах от начального значения
количества движения
до конечного
и учитывая (3.18), получим выражение для
рассматриваемой теоремы в интегральной
форме:
(3.30)
Теорема:
«Приращение
количества движения системы за конечный
промежуток времени равно векторной
сумме действующих
на
систему за это время
импульсов
внешних сил».
В
проекциях на координатные
оси
(например, Ох)
выражение (3.30)
запишем
следующим образом:
(3.31)
3.6.3.
Теорема
об изменении момента количества движения
(кинетического
момента) системы. Закон сохранения
момента
количества
движения (кинетического момента).
Дифференциальное уравнение вращательного
движения
Теорема:
«Производная
по времени от момента количества движения
системы относительно некоторого
неподвижного центра равна геометрической
сумме моментов всех внешних сил системы
относительно того же центра»
(3.32)
В
проекциях на оси декартовой системы
координат выражение (3.32) для рассматриваемой
теоремы имеет вид:
.
(3.33)
Закон
сохранения момента количества движения:
«Если
алгебраическая сумма проекций моментов
внешних сил, действующих на какую-либо
из осей, равна
нулю,
то проекция момента количества движения
на соответствующую ось постоянна»
.
В
проекциях на оси декартовой системы
координат (например, Oz)
вышестоящее
выражение для рассматриваемой теоремы
имеет вид:
;
.
Если
тело вращается вокруг оси Oz,
то, используя выражения
(3.11) и
(3.33), получим
дифференциальное уравнение вращательного
движения
.
(3.34)
3.6.4.
Теорема
об изменении кинетической энергии
системы
Теорема:
«Изменение
кинетической энергии системы при
некотором ее конечном перемещении равно
сумме работ всех приложенных к системе
внешних и внутренних сил на этом
перемещении»
.
(3.35)
Выражение
(3.35)
представляет математическую запись
теоремы
об изменении кинетической энергии в
интегральной форме.
Для
неизменяемой системы, где сумма работ
внутренних сил равна нулю, оно имеет
вид:
(3.36)
Пример.
Механическая
система под действием сил тяжести
приходит в движение из состояния покоя
(рис. 3.2).
Учитывая трение скольжения тела 1 о
наклонную плоскость и пренебрегая
другими силами сопротивления, определить
скорость тела 1 в тот момент, когда
пройденный путь будет равным s.
Дано:
m1
= m3
= 4m;
m2
= m;
R2
= R3
=
20 см; r2
= 0,75R2;
f
= 0,2; s = 1,2
м; радиус инерции блока 22
= 0,8R2.
Решение
Применим
теорему об изменении кинетической
энергии для неизменяемой системы:
гдеТ
и
Т0
– начальное и конечное значение
кинетической энергии. Так как система
в начальный момент времени находилась
в покое, то Т0
= 0, а
Т
= Т1
+
Т2
+Т3.
Тело
1 совершает поступательное движение,
его кинетическая энергия
Блок
2 совершает вращательное движение с
угловой скоростью
Определим момент инерции блока
относительно оси вращения
Кинетическая
энергия блока 2
Каток
3 совершает плоскопараллельное движение,
его кинетическая энергия
.
Мгновенный
центр скоростей катка находится в точке
Р,
поэтому его угловая скорость
Скорость точкиМ
блока 2
а
.
Скорость
центра катка 3
Момент инерции катка – сплошного,
однородного цилиндраЕго кинетическая энергия
Кинетическая
энергия всей системы
При
движении системы работу совершают
следующие силы:
–
сила тяжести тела 1
–
сила трения тела 1 о наклонную плоскость
–
сила тяжести катка 3
Сумма
работ всех внешних сил, приложенных к
системе:
.
Из
выражения
следует, что
.
Окончательно
получим
м/с.
Импульс. Работа. Энергия
Введение
Решение механических задач часто облегчается
применением законов изменения и сохранения импульса и энергии тела или системы
тел. Особенно эффективным является применение этих законов в случаях, когда
действующие на тела силы или ускорения тел переменны во времени и
непосредственное решение уравнений динамики с помощью методов «школьной»
математики затруднительно (или вовсе невозможно).
Напомним, что импульсом тела (материальной точки)
массы 
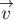
векторная физическая величина 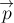
его скорость: 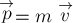
Приращение
импульса тела за малый промежуток времени 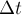
силы 
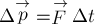
Если на тело действуют несколько сил, то под 
Если сила 
формуле можно определить приращение импульса тела за любой, уже необязательно
малый, промежуток времени 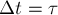
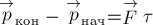
Напомним
также, что здесь и далее, если специально не оговорено обратное, под телом или
системой тел мы понимаем материальную точку или систему материальных точек
соответственно, а модуль векторной величины обозначаем той же буквой, что и
саму величину, но без стрелки над ней. Кроме того, все понятия, законы и
явления, рассматриваемые здесь, мы будем, как и прежде, излагать в инерциальных
системах отсчёта.
В начало
§1. Импульс системы тел и его изменение.
Определение 1.
Импульсом 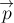
называется векторная сумма импульсов отдельных тел, составляющих
эту систему:
Рассмотрим
систему тел, взаимодействующих друг с другом и с внешними телами. Для простоты
ограничимся системой из трёх тел (рис. 2). Пусть 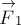
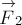
— внешние силы, действующие соответственно на первое, второе и
третье тела системы со стороны внешних тел (тел, не входящих в рассматриваемую
систему). Пусть далее 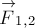
стороны второго, 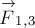
сила, действующая на первое тело со стороны третьего. Аналогично определим
силы 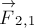
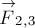
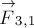
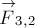
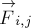
действующая на 
Применяя
закон изменения импульса (*) для каждого тела системы, запишем уравнения:
Складывая
эти уравнения почленно и частично группируя слагаемые, стоящие в правых частях
уравнений, получим
По
третьему закону Ньютона для сил взаимодействия тел системы имеем:
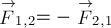
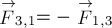
и, следовательно,
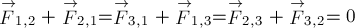
Тогда
имеем: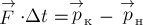
где 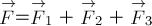
сил, действующих на систему,
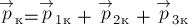
системы тел (по определению),
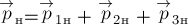
системы тел (по определению).
Обозначив разность
через 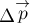
(1)
Аналогичные рассуждения можно
провести для систем, состоящих из произвольного количества тел, и убедиться в
справедливости (1) в каждом случае.
Таким образом, приращение
импульса системы тел равно импульсу суммы всех внешних сил, действующих на
систему.
Мы видим, что изменение импульса
системы тел обусловлено действием только внешних сил (т.е. сил,
действующих со стороны тел, не входящих в систему), а внутренние силы, какой
бы природы они ни были, импульс системы изменить не могут.
Кроме того, приращение импульса
системы тел сонаправлено с вектором суммарной внешней силы 
ПРИМЕР 2.
Два груза массами 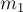
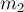
В некоторый момент нить аккуратно перерезают. Чему равно приращение импульса
системы тел «грузы + пружина» за время 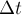
Сопротивлением воздуха пренебречь.

РЕШЕНИЕ. После
перерезания нити указанная система тел начинает свободно падать. Силы
взаимодействия грузов и пружины являются для рассматриваемой системы
внутренними силами и импульс системы изменить не могут. На грузы также действуют
силы тяжести со стороны Земли (рис. 3б), которые для системы являются внешними
(т.к. Земля в рассматриваемую систему не входит и, следовательно, является
внешним телом). Силой тяжести пружины пренебрегаем, т.к. по условию пружина
лёгкая (т.е. её массу можно считать равной нулю).
В соответствии с (1) для
приращения импульса системы тел можно записать
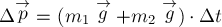
Таким образом
вектор 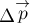
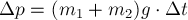
вертикально вниз (в сторону суммарной силы тяжести).
В начало
§2. Законы сохранения импульса тела и системы тел.
Сказанное позволяет
сформулировать законы сохранения импульса тела и системы тел. Действительно, в
случаях, когда правые части уравнений (*) и (1) можно считать равными нулю, то
и приращения импульса тела и импульса системы тел соответственно будут также
равны нулю. Это означает, что в таких случаях указанные импульсы будут
оставаться неизменными, то есть сохраняться.
Закон сохранения импульса тела:
импульс тела сохраняется, если импульс равнодействующей всех сил,
действующих на это тело, равен нулю. Это возможно в случаях, когда
- на тело не действуют силы вообще или
- равнодействующая всех сил, действующих на тело, равна нулю, или
- промежуток времени
, в течение которого мы наблюдаем за состоянием тела, очень
мал (стремится к нулю), а равнодействующая всех сил, действующих
на тело, ограничена по модулю (не бесконечно большая).
В первом пункте
сформулированного закона речь идёт о так называемом свободном теле,
которое будет покоиться или двигаться по инерции до тех пор, пока воздействия
со стороны других тел не выведут его из этого состояния (вспомните 1-й закон
Ньютона). Второй пункт представляется очевидным, а ограничение модуля
равнодействующей в третьем пункте необходимо для того, чтобы исключить случаи
возникновения математической неопределённости произведения бесконечно больших и
бесконечно малых величин (неопределённости типа 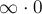
ПРИМЕР 3.
Снаряд, летящий
в воздухе, разрывается на несколько осколков. Сохраняется ли при взрыве импульс
снаряда?
ОТВЕТ. Да, сохраняется.
Действительно, на снаряд действуют сила тяжести со стороны Земли и сила
сопротивления воздуха. Модули обеих сил имеют конкретные значения, зависящие от
массы снаряда (для силы тяжести) и от скорости снаряда относительно воздуха
(для силы сопротивления). Эти значения ограничены по величине. Следовательно, и
равнодействующая этих сил ограничена по модулю. В свою очередь время взрыва
мало (взрыв происходит «мгновенно»). Таким образом импульс снаряда при взрыве
сохраняется.
Здесь полезно заметить, что в
соответствии с определением 1 под импульсом снаряда после взрыва следует понимать
суммарный импульс образовавшихся при взрыве осколков.
Закон сохранения импульса системы тел:
импульс системы тел сохраняется при любых взаимодействиях
тел системы, если импульс суммы всех внешних сил, действующих на
систему, равен нулю. Это возможно в случаях, когда
- внешние силы на систему не действуют (т.е. тела системы взаимодействуют только между собой) или
- внешние силы на систему действуют, но их сумма равна нулю (силы взаимно уравновешиваются), или
- промежуток времени
, в течение которого мы наблюдаем за состоянием системы,
очень мал (стремится к нулю), а суммарная внешняя сила
ограничена по модулю (не бесконечно большая).
Здесь в первом пункте речь идёт
о системах, не взаимодействующих с внешними телами. Такие системы называются замкнутыми
или изолированными. Конечно, это идеализация. В реальности у тел системы
всегда будет присутствовать взаимодействие с другими телами, не входящими в
систему. Однако если это взаимодействие не оказывает сколь-нибудь заметного
влияния на состояние системы, то такую систему тел в большинстве случаев можно
считать замкнутой.
Второй пункт представляется
очевидным, а в третьем пункте, как и ранее, ограничение на модуль суммы внешних
сил наложено с целью избежать неопределённости типа 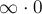
ПРИМЕР 4.
Человек массой 
поверхности озера. Человек совершил вдоль плота перемещение 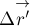
остановился. Сопротивление воды пренебрежимо мало. Чему при этом будет равно
соответствующее перемещение 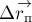
РЕШЕНИЕ. На плот
действуют сила тяжести, сила Архимеда и вес человека. На человека действует
сила тяжести и сила реакции плота. Рассматривая систему тел «человек + плот»,
видим, что вес человека и сила реакции плота являются внутренними силами, силы
тяжести человека и плота и сила Архимеда – внешними. Сумма внешних сил равна
нулю, следовательно импульс системы меняться не будет, оставаясь равным нулю в
процессе движения: 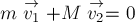
где 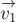
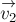
скорости человека и плота относительно берега. Скорость человека относительно
берега можно представить в виде 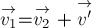
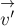
скорость человека относительно плота. Исключив 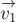
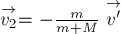
Умножив обе части на
время 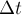
относительно берега: 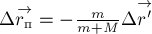
Знак «минус» показывает, что это
перемещение происходит в направлении, противоположном направлению перемещения
человека относительно плота.
У незамкнутой системы сам
импульс 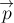
проекция 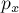
- внешние силы, действующие на систему, направлены перпендикулярно оси Ох или
- алгебраическая сумма проекций на ось Ох всех внешних сил, действующих на систему равна нулю, или
- промежуток времени
, в течение которого мы наблюдаем за состоянием системы,
очень мал (стремится к нулю), а алгебраическая сумма
проекций на ось ОX всех внешних сил, действующих на тело, ограничена по модулю
(не бесконечно большая).
ПРИМЕР 6.
Кузнечик
массой 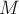
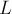
гладком горизонтальном полу. Кузнечик прыгает и попадает на другой конец
соломинки (рис. 4а). С какой минимальной начальной скоростью относительно пола
он должен прыгать, если масса соломинки 
пренебречь.

РЕШЕНИЕ. Направим ось 0Y
вертикально вверх, а ось 0X – горизонтально вдоль соломинки по
направлению прыжка кузнечика (рис. 4б). Обозначим начальную скорость кузнечика
относительно пола через 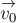
горизонтом через 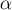
соответственно равны 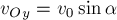
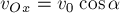
Рассмотрим систему «кузнечик +
соломинка». На тела системы внешние силы действуют лишь вдоль вертикального
направления, то есть направлены перпендикулярно оси 0X. Отсюда следует,
что проекция на ось 0X импульса системы сохраняется и остаётся равной
нулю. Тогда можно записать: 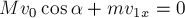
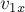
0х скорости 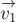
которую приобрела соломинка относительно пола сразу после прыжка
кузнечика. Отсюда видно, что 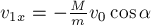
соломинка получает скорость, направленную противоположно оси 0х, а
модуль скорости равен 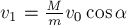
Заметим, что в направлении оси 0Y
проекция импульса системы не сохраняется, так как в момент отрыва кузнечика от
соломинки у него появляется проекция скорости 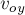
было. Следовательно, возникает проекция 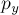
равная 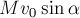
изменяется из-за действия силы тяжести.
Далее по
формулам кинематики время полёта кузнечика равно 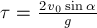
дальность прыжка кузнечика (вдоль оси 0х) 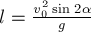
За время tau
соломинка переместится по полу на расстояние 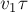
противоположную оси 0х (рис. 4б). Чтобы кузнечик «не промахнулся» и точно
попал на другой конец соломинки, очевидно должно выполняться условие: 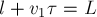
С учётом выражений для 
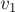
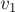
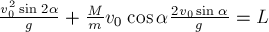
Откуда находим
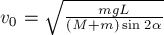
Видим, что модуль скорости
кузнечика относительно пола минимален, когда максимален знаменатель дроби
полученного выражения. Как известно, максимальное значение синуса равно 1. Итак
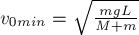
В начало
§3. Центр масс системы тел
Часто при решении задач бывает
удобно воспользоваться понятием центра масс системы тел.
Определение 2.
Центром
масс системы тел называется точка С, радиус-вектор которой
определяется по формуле
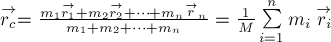
Здесь 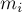
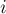
тела системы, 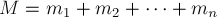
тел, 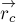
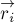
радиус-вектор 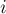

Аналогично определяется центр
масс тела в случаях, когда при решении задачи это тело нельзя считать
материальной точкой. Тогда обычно поступаю так. Мысленно «разбивают» тело на
множество сколь угодно малых частей, каждую из которых уже можно считать
материальной точкой, и рассматривают данное тело как систему из полученных
материальных точек. При этом в определении центра масс под величиной 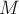
надо понимать массу всего тела, которая, естественно, равна сумме масс его
частей.
Можно показать, что
- положение точки С относительно тела не зависит от выбора начала отсчёта
системы координат, - центр масс однородного центральносимметричного тела совпадает с его
центром симметрии, - центр масс однородного осесимметричного тела лежит на оси симметрии
тела, - в однородном поле тяжести (например вблизи поверхности Земли) центр масс
тела совпадает с его центром тяжести, - иногда при решении задач можно мысленно сосредоточить в центре масс всю
массу тела и, считая тело материальной точкой, применять законы механики для
материальной точки.
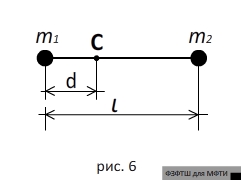
Полезно также знать, что центр
масс треугольной пластины постоянной пренебрежимо малой толщины лежит на
пересечении медиан соответствующего треугольника, а центр масс системы двух
материальных точек массами 
С, отстоящей от 
убедиться, напрямую воспользовавшись приведённым выше определением центра
масс.
Для нахождения центра масс
системы нескольких тел, которые нельзя считать материальными точками, можно,
следуя описанной выше процедуре, найти центры масс каждого из тел, а затем
заменить тела материальными точками, сосредоточив массы тел в их центрах масс,
и найти центр масс системы этих материальных точек.
ПРИМЕР 7.
На столе лежат
постоянной толщины плоский диск массой 
массой 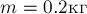
центром 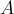
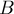
равно 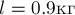
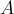
находится центр масс данной системы тел?
РЕШЕНИЕ. Центры масс
диска и треугольной пластины находятся в точках 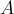
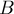
совпадает с центром масс системы материальных точек с массами 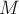

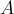
и 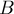
Пусть 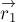
и 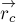
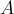
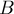
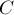
Тогда положения этих точкек относительно точки 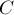
радиус-векторами
После подстановки в эти
равенства согласно (2) выражения
получим:
Отсюда следует, что векторы 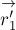
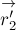
коллинеарны и противоположно направлены ( 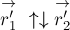
точка 
и 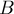
расстояния 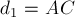
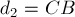
пропорциональны массам соответствующих материальных точек:
Отсюда, учитывая,
что 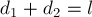
центра 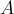

В начало
§4. Теорема о движении центра масс
По определению 2 радиус-вектор 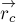
времени 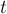
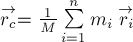
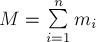
системы).
Через малый промежуток
времени 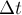
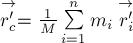
первое, получим
Если умножить обе части
уравнения на 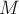
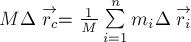
Разделим обе части на малую, но
всё же отличную от нуля, величину 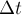
Учитывая,
что 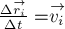
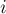
а 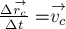
В правой части полученного
уравнения стоит импульс рассматриваемой системы тел (по определению). Таким
образом мы получили, что импульс системы тел равен произведению массы
системы на скорость её центра масс:
Рассуждая аналогичным образом,
получим, что приращение импульса системы тел за малый промежуток
времени 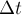
масс:
Учитывая уравнение (1), можно
записать 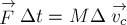

действующих на систему.
Разделив обе
части (3’) на 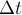
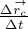
точки С, получим 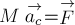
Таким образом можно
сформулировать теорему о движении центра масс:
в инерциальной системе
отсчёта центр масс системы тел (материальных точек) движется так, как двигалось
бы тело (материальная точка), масса которого равна массе системы, под действием
силы, равной сумме всех внешних сил, действующих на систему.
Иногда эту теорему называют
вторым законом Ньютона для системы тел.
Рассмотрим применение теоремы о
движении центра масс на практике. В частности покажем, как можно
иначе решить задачу с человеком на плоту (см. Пример 4), если воспользоваться
понятием центра масс и указанной теоремой.
ПРИМЕР 8.
Человек
массой 
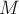
поверхности озера. Человек совершил вдоль плота перемещение 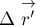
остановился. Сопротивление воды пренебрежимо мало. Чему при этом будет равно
соответствующее перемещение 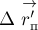
РЕШЕНИЕ. Так как
сопротивление воды пренебрежимо мало, то сумма всех внешних сил, действующих на
систему «человек + плот» равна нулю. По теореме о движении центра масс это
означает, что ускорение центра масс данной системы равно нулю, и,
следовательно, положение центра масс системы в процессе движения человека (и
плота) меняться не будет (т.к. в начальный момент по условию плот и человек
покоились). Тогда в соответствии с (2) имеем: 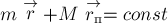
где 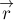
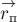
положения центров масс человека и плота относительно некоторой точки берега. Из
этого равенства найдём связь между приращениями векторов 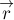
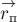
промежуток времени 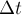
Имея в виду, что приращения 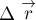
и 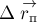
относительно берега, причём 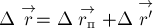
перемещение плота 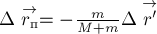
ПРИМЕР 9.
Однородный
стержень длины 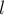
поверхности. Верхний конец стержня подвешен на нити так, что стержень образует
с горизонтальной плоскостью угол 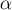
сторону и на сколько сместится нижний конец стержня, когда он упадёт?
РЕШЕНИЕ. Так как в
горизонтальном направлении на стержень никакие силы не действуют, то его центр
масс будет двигаться вертикально вниз, как материальная точка, масса которой
равна массе стержня, падающая без начальной скорости.
Центр масс однородного стержня
находится посередине стержня на расстоянии 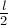
концов. С учётом этого в момент падения нижний конец стержня сместится влево на
расстояние 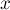

ПРИМЕР 10.
Человек
прыгает с вышки в воду с начальной скоростью, составляющей некоторый угол с
горизонталью. Движение прыгуна в общем случае имеет весьма сложный характер.
Однако если сопротивление воздуха пренебрежимо мало, то можно сразу утверждать,
что центр масс прыгуна движется по параболе, как материальная точка, на которую
действует постоянная сила тяжести 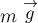

При доказательстве теоремы о
движении центра масс было получено важное утверждение, записанное в виде
уравнения (3). С его помощью, зная массу системы тел и скорость её центра масс,
можно установить, чему равен импульс системы, не складывая импульсы отдельных
тел системы.
ПРИМЕР 11.
Однородный
обруч массы 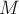
проходящей через его геометрический центр. Чему равен импульс обруча, если ось
вращения неподвижна?
ОТВЕТ. Центр масс
однородного обруча находится в его геометрическом центре. Эта точка по условию
неподвижна, т.е. скорость центра масс обруча равна нулю 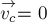
Таким образом импульс обруча равен нулю: 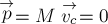

ПРИМЕР 12.
С
горизонтальной поверхности земли бросили под углом 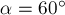
скоростью 
большей массы бросили с поверхности земли под углом 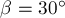
причём начальные скорости комков оказались лежащими в одной вертикальной
плоскости (рис. 9а). В результате столкновения комки слиплись. Найдите скорость
(по модулю) упавшего на землю слипшегося комка. (МФТИ, 1984 г.)
РЕШЕНИЕ. Направим оси
прямоугольной декартовой системы координат, как показано на рис. 9б. Начало
отсчёта поместим в току бросания первого комка. Пренебрегая сопротивлением
воздуха, для координат по оси 0у комков в произвольный момент времени
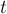
В момент 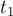
полёте их координаты сравниваются 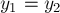
Отсюда получаем, что
Центр масс системы, состоящей из
двух рассматриваемых комков, по теореме о движении центра масс будет двигаться
аналогично телу, брошенному под углом к горизонту. Тогда скорость слипшегося
комка непосредственно перед ударом о землю (искомая скорость) равна по модулю
скорости центра масс системы комков в момент бросания. Обозначим эту скорость
через 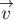
Определение 1, получим:
где 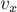
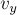
системы комков на соответствующие оси координат, 
комка. По условию масса второго комка равна 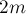
Далее, учитывая полученное выше выражение,
связывающее 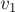
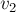
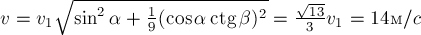
В начало
§5. Работа силы. Мощность силы.
Изменение импульса тела (или
системы тел) характеризует действие суммарной силы (или суммы внешних сил) в
течение конкретного промежутка времени. Для характеристики действия силы на
некотором перемещении служит физическая величина, называемая механической
работой.
Пусть на прямолинейно движущееся
тело действует постоянная сила 
совершило перемещение 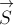
Определение 3.
Работой 
постоянной силы 
величина, равная скалярному произведению вектора силы 
перемещения 
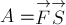
Согласно определению скалярного
произведения векторов 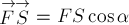
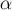
между векторами 
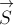
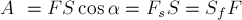
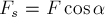

направление вектора 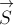
проекция вектора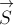

По определению работы, она
является скалярной величиной и понятие направления, следовательно к работе
неприменимо.
В системе единиц СИ единицей
измерения работы служит джоуль (Дж): ![[A] = H m = кг м/с^2 = Дж](http://mipt-bot.narod.ru/cache/tex/fba4b28e535979387df76e5c511cc54e.png)

Для работы можно дать наглядное
графическое представление. Если отложить по оси абсцисс текущее
положение 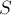
тело, а по оси ординат – значение проекции 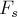
когда 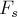
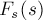
параллельной оси абсцисс (рис. 12). Если тело совершает перемещение 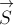
то работа силы 
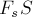
численно равна площади прямоугольника со сторонами 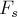
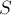
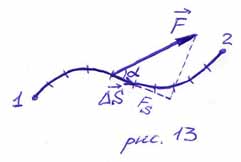
Пусть теперь тело движется по
некоторому, в общем случае криволинейному, участку траектории 1-2
(рис.13). Пусть также на тело действует сила 
случае в процессе движения может меняться как по модулю, так и по направлению.
Мысленно разобьём траекторию движения тела на множество малых элементарных участков,
в пределах каждого из которых проекцию силы на направление
перемещения 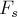
различной), а сами участки – прямолинейными. Рассмотрим малое
перемещение 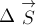
Определение 4.
Элементарной
работой 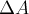

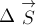
величина, равная скалярному произведению векторов 
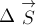
И вновь, как и прежде, можно
написать:
(5)
где 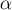

, 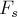

, 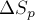
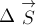

Определение 5.
Работой
силы 
алгебраической сумме элементарных работ (5), совершаемых этой силой на каждом
из элементарных участков.
Таким образом можно записать:
(6)
где 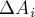

-м элементарном участке.
Выражению (6) можно придать
наглядный геометрический смысл. Рассматривая 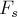
тела на траектории, т.е. функцию дуговой координаты 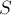
график 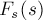
рис. 14. Элементарная работа 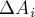
заштрихованного «столбика» (прямоугольника со сторонами 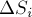
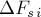
а работа на всём участке траектории от точки 1 до
точки 2 будет равна алгебраической сумме площадей таких «столбиков» для
всех элементарных участков, причём площади столбиков над осью 0S
берутся со знаком «плюс» (они соответствуют положительной работе), а площади под осью 0S
– со знаком «минус» (они соответствуют отрицательной
работе). Таким образом работа силы 
разности площадей фигуры 1АЕ над осью абсцисс и фигуры ЕВ2 под
осью абсцисс.
ПРИМЕР 15.
Пружина
жесткости 
лежащему на гладком горизонтальном столе, расположена горизонтально и сжата.
Деформация пружины равна 
упругости по перемещению груза в процессе перехода пружины в недеформированное
состояние (рис. 15а).

РЕШЕНИЕ. В
первоначальном положении, когда пружина сжата на величину 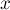
упругости, действующая на груз равна 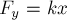
пружины груз переместился на расстояние 
уменьшилась на величину 
упругости 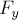
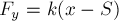
Построив график
зависимости 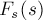
получим отрезок прямой, проходящей через точки с координатами (
) и (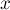
треугольника:
В дополнение к сказанному
следует особо отметить, что если та или иная сила совершает работу, это не
означает, что тело движется благодаря именно этой силе. В реальных ситуациях на
тело действуют несколько сил (порой, много), и движение тела обусловлено
совместным действием всех сил. При этом работа отдельных сил как правило
различна. Чтобы в этом убедиться, достаточно вернуться к Примеру 14. Однако
часто бывает нужно знать общую работу всех (либо части сил), действующих на
тело. Тогда в общем случае для 
сумме механических работ каждой из сил в отдельности:
И ещё. Если мы имеем дело не с
материальной точкой, а с твёрдым телом или системой тел, то данные выше
определения 3 и 4 остаются справедливыми, но в этом случае надо только иметь в
виду, что под 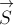
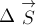
точки приложения силы. Игнорирование этого обстоятельства зачастую приводит
к ошибочным результатам.
Пусть за промежуток
времени 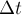

работу 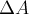
Определение 6.
Средней мощностью
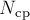

времени 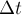
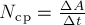
С учётом (5) можно записать
Устремляя в полученном равенстве
величину 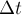
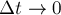
мгновенную скорость 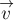
Определение 7.
Мгновенной
мощностью силы 
произведению вектора силы 
тела, к которому приложена эта сила.
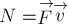
При этом характер зависимости
силы 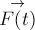
Единицей измерения мощности в
системе СИ служит ватт (Вт):
Развитие технического прогресса
привело к созданию огромного числа машин и механизмов, действие которых также
принято характеризовать мощностью. В этом случае мощность представляет собой
величину работы, которую совершает или может совершить та или иная машина в
единицу времени. Но с другой стороны в нашем рассмотрении работу совершают
конкретные силы, а не отвлечённые машины и механизмы. В связи с этим при
решении задач во избежание недопонимания надо прежде всего выяснить, какие силы
совершают работу в каждом конкретном случае и лишь затем применять понятие
мощности машины или механизма, понимая под ней суммарную мощность этих сил.
ПРИМЕР 18.
Машина в
течение получаса совершает над телом работу, равную 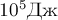
равна средняя мощность, развиваемая этой машиной?
РЕШЕНИЕ. Здесь под
мощностью машины понимается суммарная мощность всех сил, действующих на тело со
стороны машины. Эти силы совершают указанную в условию суммарную
работу 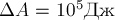
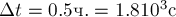
Средняя мощность машины по формуле
(7) равна
Часто при решении задач,
связанных с работой машин и механизмов, используется понятие полезной мощности,
которая равна 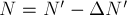
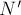
при отсутствии трения в её деталях (полная мощность), а 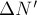
часть мощности, необходимая на преодоление сил трения в деталях машины во время
её работы.
Определение 8.
Отношение
полезной мощности 
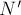
коэффициентом полезного действия
(сокращённо — КПД) машины или механизма:
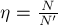
КПД принято выражать в процентах
(%), для чего следует домножить выражение (9) справа на 100%.
В начало
§6. Кинетическая энергия
Часто говорят о работе, которую
совершает или может совершить над телом какое-либо другое тело. Здесь, во
избежание недоразумений, надо понимать, что работу над телом совершает сила,
действующая на него со стороны рассматриваемого другого тела.
Способность тела совершать
работу характеризуют с помощью энергии.
Тело может обладать энергией
вследствие
- своего движения (кинетическая энергия),
- взаимодействия с
другими телами или (для системы тел и тела – не материальной точки)
взаимодействия отдельных частей тела между собой (потенциальная энергия - вследствие хаотического движения и взаимодействия молекул внутри тела (внутренняя
энергия).

Пусть на тело
массы 
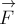
с постоянным ускорением 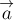
за промежуток времени 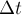
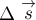
скорость изменилась от величины 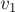
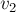
работа, совершённая силой 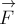
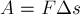
Или с учётом второго закона Ньютона 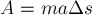
кинематики известно, что при равноускоренном движении
Тогда работа 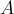
равна:
Определение 9.
Кинетической энергией
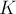
произведения массы 
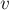
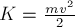
Таким образом можно записать,
что
Если на тело действуют несколько
сил, тогда в правой части полученного уравнения будет стоять суммарная работа
всех сил на указанном перемещении.
Обобщив сказанное выше, можно
сформулировать
теорему об изменении кинетической энергии тела: приращение
кинетической энергии тела на некотором перемещении равна алгебраической сумме
работ всех сил, действующих на тело на том же перемещении
Это утверждение остаётся
справедливым и в общем случае, когда переменные по величине и направлению силы
действуют на криволинейном участке траектории. Заметим, что кинетическая
энергия является скалярной величиной и в системе СИ измеряется (как и работа) в
джоулях (Дж).
ПРИМЕР 20.
По
горизонтальной поверхности движется небольшой брусок массой 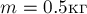
В некоторый момент времени его кинетическая энергия равна 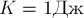
скорость бруска в этот момент?
РЕШЕНИЕ. По определению 9
кинетическая энергия тела равна 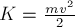
Отсюда
ПРИМЕР 21.
Пуля
массы 
массы 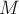
скорость пули уменьшается вдвое (рис. 18а). Чему равна начальная скорость пули,
если брусок продвинулся по столу на расстояние 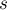
трения бруска о поверхность стола равен 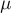
поступательное.
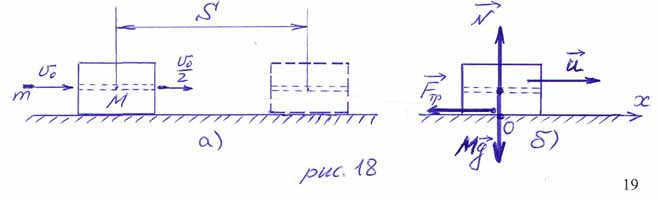
РЕШЕНИЕ.
Пусть 
сила трения скольжения со стороны поверхности стола, сила тяжести и сила
нормальной реакции опоры (рис. 18б). На пулю действует сила тяжести. При
пролёте пули через брусок на неё дополнительно действует сила сопротивления
движению со стороны бруска. Такая же по модулю сила действует и на брусок со
стороны пули.
Рассматривая систему тел «пуля +
брусок», видим, что силы взаимодействия пули с бруском являются внутренними.
Остальные силы внешние и ограничены по величине. Кроме того, время пролёта пули
через брусок мало. Таким образом импульс системы за этот промежуток времени
сохраняется. В проекциях на ось 0х имеем:
При дальнейшем движении бруска
по столу приращение кинетической энергии бруска равно 
Учитывая, что конечная кинетическая энергия 
остановился), а начальная 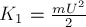
При движении бруска сила тяжести
и сила нормальной реакции опоры работы не совершают (направлены перпендикулярно
перемещению), а работа силы трения скольжения
равна 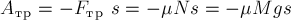
образом по теореме об изменении кинетической
энергии 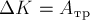
Отсюда получаем, что 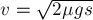
и после подстановки в уравнение закона сохранения импульса находим начальную
скорость пули:
Кинетическая энергия системы тел
равна алгебраической сумме кинетических энергий отдельных тел системы.
Для определения кинетической
энергии твёрдого тела (не материальной точки) его следует мысленно разбить на
множество маленьких частей, каждую из которых можно считать материальной
точкой. Тогда кинетическая энергия тела будет равна алгебраической сумме
кинетических энергий этих материальных точек:
(12)
В случае, когда тело (или
система) массы 
составляющих его (или систему) материальных точек в каждый конкретный момент
времени одинаковы и равны скорости 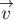
масс тела (или системы). Тогда кинетическая энергия тела (системы) в каждый
момент времени равна
Очевидно,
что 
(системы тел) массой 
скоростью 
Если движение тела (системы) не
поступательное, т.е. присутствует вращение, то для нахождения кинетической
энергии тела (системы) приведённая формула неприменима и следует пользоваться
общей формулой (12)!
Сказанное следует учитывать при
решении задач. При этом следует также иметь в виду, что теорема об изменении
кинетической энергии (11), сформулированная нами для тела, являющегося
материальной точкой, остаётся справедливой и для системы тел, и для тел, не
являющихся материальными точками. При этом под величиной 
правой части (11), по-прежнему надо понимать работу всех сил,
действующих на все тела системы. Именно всех сил, как внешних, так и внутренних!
ПРИМЕР 23.
С наклонной
плоскости одновременно без начальных скоростей начинают соскальзывать брусок и
скатываться без проскальзывания обруч. При каком коэффициенте трения скольжения
между бруском и наклонной плоскостью оба тела будут двигаться, не обгоняя друг
друга? Угол наклона плоскости к горизонту равен 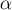
РЕШЕНИЕ. Из динамики
известно, что ускорение 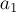
вниз, равно
Пусть обруч скатывается с наклонной
плоскости в течение времени 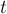
путь 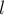
обруча в конце этого пути равна 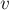
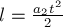
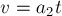
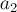
Приращение кинетической энергии
обруча за время 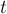
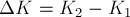
Поскольку 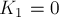
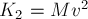
то 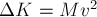
изменении кинетической энергии эта величина равна работе всех сил, действующих на
обруч в течение времени 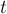
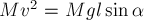
где 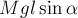
(покажите это самостоятельно). Сила нормальной реакции опоры работы не
совершает, так как направлена перпендикулярно перемещению центра масс обруча.
Работа силы трения также равна нулю, так как обруч катится без проскальзывания
и, следовательно, в каждый момент времени скорость точки касания обруча с
наклонной плоскостью (точки приложения силы трения) равна нулю. Учитывая
кинематические уравнения, найдём 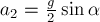
Тела не будут обгонять друг друга,
если 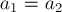
В начало
§7. Потенциальная энергия
Область пространства, в каждой
точке которой на помещённое туда тело действует некоторая определённая сила,
называется силовым полем.
В формулировке теоремы об
изменении кинетической энергии тела не содержится каких-либо ограничений на
характер действующих сил. Тело может находиться в поле любых сил.
Вместе с тем силы, действующие
на тело, могут различаться по своей природе и свойствам. В механике сложилось,
в частности, разделение сил на консервативные и неконсервативные.
Консервативными
(потенциальными) называются силы, работа которых не зависит о формы
траектории движения тела, а определяется лишь начальным и конечным его
положением.
Такими силами являются, например, сила тяжести и сила упругости пружины.
ПРИМЕР 24.
Небольшое тело
массы 
двум горкам различного профиля (рис. 20а). Чему равна работа силы тяжести тела
в обоих случаях? Точки 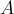
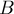
на высотах 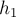
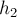

РЕШЕНИЕ.Рассмотрим
движение тела по траектории 
Сила тяжести направлена вертикально вниз и составляет некоторый (постоянный)
угол 
20б). Пусть длина отрезка АВ равна 
тяжести в этом случае будет равна: 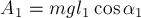
Но 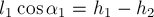
В случае движения тела по
траектории II мы имеем дело с двумя отрезками пути АС и СВ(рис.
20в). Пусть отрезок АС составляет угол 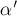
тяжести. Тогда, положив длину этого отрезка, равной 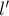
тяжести на этом участке траектории
имеем: 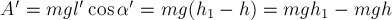
, где 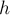
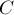
силы тяжести на участке ВС длиной 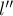
равна 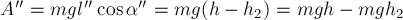
, где 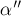
Работа 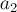
на каждом из участков траектории,
т.е. 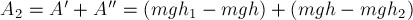
Видим, что работы силы тяжести в
обоих случаях равны и не зависят от формы траектории движения тела, а
определяются лишь начальным и конечным положениями тела, а именно – их
высотами 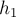
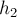
Неконсервативными (непотенциальными)
силами называются силы, работа которых зависит от формы траектории движения
тела (пройденного телом пути).
Неконсервативными являются, например, сила
трения скольжения, силы сопротивления воздуха или жидкости (силы, зависящие от
скорости тела) и т.п.
ПРИМЕР 25.
В условиях
предыдущего примера определите работу силы трения в обоих случаях, если
коэффициенты трения на участках АС и СВ траектории II одинаковы и
равны коэффициенту трения 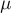
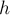
с горизонтом участки АВ, АС и СВ траекторий I и II
считать известными.

РЕШЕНИЕ. При движении
тела по траектории I (отрезок АВ) работа силы трения скольжения равна
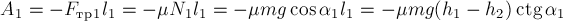
где 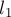
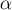
наклона поверхности горки к горизонту (рис. 21а) . Знак «минус» возник
из-за того, что направление силы трения составляет угол 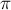
движения, а 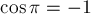
Аналогично при движении тела по
траектории II (отрезки АС и СВ) суммарная работа силы трения
будет равна (рис. 21б) 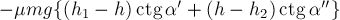
где 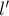
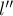
а 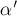
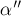
Видим, что 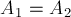
Работы силы трения определяются длинами путей, пройденных телом, а они в разных
случаях – разные.
В общем случае работа
консервативной силы может быть представлена как убыль некоторой
величины 
в поле этой консервативной силы: 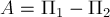
(Убыль величины отличается от приращения этой величины
знаком: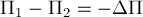
Так в случае с силой тяжести её
работа над телом равна убыли величины 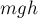
высоты, на которой оно находится (см. Пример 24):
Следовательно, потенциальная
энергия тела массы 
равна 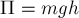
Можно показать, что работа силы
упругости пружины над телом определяется убылью величины 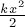
зависящей от коэффициента упругости 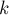
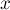
Значит, потенциальная энергия
тела в поле упругой силы деформированной пружины
равна 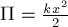
определяется только параметрами пружины (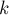
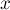
величину 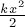
потенциальной энергией пружины (а не тела).
Для работы неконсервативных
сил (трения, сопротивления и др.) равенство (13) несправедливо и понятие
потенциальной энергии тела в поле неконсервативных сил не вводится!
Потенциальная энергия
тела уравнением (13) определяется неоднозначно. К ней можно добавить (или
вычесть) любую постоянную и от этого работа 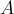
консервативной силы не изменится, так как не изменится разность значений
потенциальной энергии 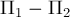
уровень, от которого «отсчитывается» потенциальная энергия. Например, в
случае с телом, поднятым с поверхности земли на некоторую высоту, нулевым
уровнем можно считать и поверхность земли, и дно расположенного вблизи оврага и
уровень высоты кустарника, растущего вдоль берега оврага и т.п. Следовательно,
при решении задач необходимо сначала выбрать нулевой уровень и затем, сохраняя
его неизменным в процессе решения, отсчитывать от него потенциальную энергию
тела, на которое действует соответствующая консервативная сила.
При определении потенциальной
энергии поднятого над землёй тела в поле силы тяжести за нулевой уровень обычно
принимается поверхность земли.
Для тела, находящегося в поле
силы упругости деформированной пружины, обычно считается, что его потенциальная
энергия равна нулю в положении, когда пружина не деформирована.
Исходя из сказанного,
потенциальную энергию тела, находящегося в поле консервативной силы, можно
определить следующим образом. Выберем положение тела, в котором будем считать
его потенциальную энергию равной нулю (т.е. выберем нулевой уровень). Тогда потенциальной
энергией тела в некоторой произвольной точке поля будем называть величину,
равную работе, которую может совершить консервативная сила над телом, если тело
переместится из этой точки в точку с нулевой потенциальной энергией.
В начало
§8. Закон сохранения механической энергии тела. Столкновения.
Пусть на тело действуют
несколько сил, например – две, как показано на рис. 22. Пусть, кроме того,
сила 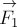
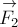
Тогда работа 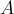
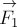
тела: 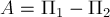
изменении кинетической энергии, приращение кинетической энергии тела равно
суммарной работе обеих сил:
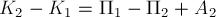
где 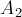
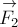
Перенесём слагаемые с
потенциальной энергией в левую часть уравнения и сгруппируем их с
соответствующими кинетическими энергиями:
Определение 10.
Физическую
величину, равную сумме кинетической и потенциальной энергий тела называют механической
энергией тела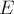
Учитывая это определение в
рассматриваемом случае, имеем: 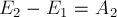
где 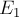
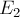
механической энергии тела соответственно.
В общем случае на тело могут
действовать несколько неконсервативных сил. Тогда в правой части полученного
уравнения будет стоять суммарная работа этих сил. С учётом этого можно
утверждать, что приращение механической энергии
тела равно суммарной работе 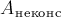
тело в процессе его движения: 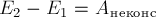
Если 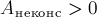
механическая энергия тела увеличивается, если 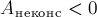
уменьшается.
ПРИМЕР 26.
Тело
массы 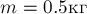
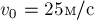
горизонту с обрыва высотой 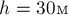
работу совершила сила сопротивления воздуха за время полёта тела, если непосредственно
перед падением в воду скорость тела была равна
РЕШЕНИЕ. В процессе
падения на тело действуют две силы: сила тяжести и сила сопротивления воздуха.
Первая сила консервативная, вторая – нет. Приращение механической энергии тела
за время полёта равно:
С другой стороны, согласно (14),
это приращение равно искомой работе неконсервативной силы сопротивления
воздуха:
Подставляя в полученное
уравнение численные значения величин, найдём:
Интересно, что полученная
величина в общем случае может оказаться не только отрицательной, но и
положительной. Это зависит, например, от наличия и характера ветра в процессе
падения тела.
Среди всевозможных
неконсервативных сил силы трения (сопротивления) совершают, как правило,
отрицательную работу (не всегда!). В этом случае механическая энергия тела в
процессе движения уменьшается. Одновременно, как известно, работа сил трения
производит нагревание трущихся тел. Часть механической энергии тела переходит в
тепловую (внутреннюю) энергию движения молекул, составляющих тела, то есть
выделяется некоторое количество теплоты 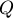
равно по модулю работе сил трения и, следовательно, убыли механической энергии
тела (при отсутствии иных неконсервативных сил).
Если же неконсервативные силы на
тело не действуют или действуют, но таковы, что их суммарная работа равна нулю,
то и приращение механической энергии равно нулю. Отсюда непосредственно
вытекает закон сохранения механической энергии тела:
Если неконсервативные силы на
тело не действуют или таковы, что не совершают работы в течение интересующего
нас времени, то механическая энергия тела остаётся постоянной за это время:
Заметим, что здесь речь идёт о
сохранении именно суммы кинетической и потенциальной энергии тела. Сами же эти
энергии могут изменяться по отдельности. Однако эти изменения происходят так,
что приращение одной из них в точности равно убыли другой. Иными словами имеют
место взаимные превращения кинетической и потенциальной энергий тела. Энергия
не исчезает и не возникает вновь, она переходит из одного вида в другой.
Потенциальная энергия может переходить в кинетическую (например, при свободном
падении тела), кинетическая – в потенциальную (прогибание батута при прыжках
гимнаста), потенциальная энергия одного вида – в потенциальную энергию другого
(взвешивание на пружинных весах, когда потенциальная энергия груза в поле
тяжести напрямую переходит в потенциальную энергию груза в поле упругих сил).
Во всех этих случаях механическая энергия тела остаётся постоянной.
ПРИМЕР 28.
Лёгкая
пружина жёсткости 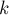
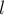
поверхности стола. С высоты 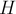
пружину падает шарик массой 
упругости пружины в процессе взаимодействия с шариком. Сопротивлением воздуха
пренебречь.

РЕШЕНИЕ. При свободном
падении шарика его потенциальная энергия в поле тяжести переходит в
кинетическую энергию движения (скорость шарика увеличивается по мере уменьшения
высоты шарика над столом) вплоть до момента касания шариком пружины. Далее по
мере сжатия пружины кинетическая энергия шарика и его потенциальная энергия в
поле тяжести переходят в потенциальную энергию шарика в поле силы упругости
пружины (сила упругости пружины возрастает за счёт уменьшения скорости шарика и
его высоты над столом). Когда скорость шарика обратится в ноль, сила упругости
достигнет своего максимального значения. Поскольку на шарик в течение всего
времени движения действуют только консервативные силы, то механическая энергия
шарика сохраняется: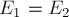
длина пружины равна 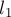
механической энергии

Выразив отсюда 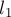
максимальной силы упругости пружины получаем:
Таким образом,
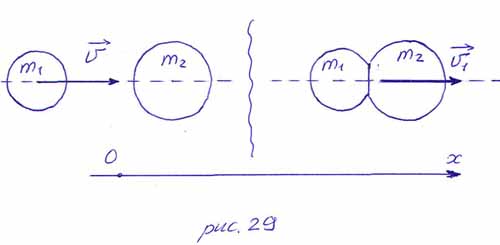
ПРИМЕР 29.
Два груза
массой 
пружина, сжатая на величину 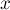
скоростью 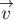
Нить пережигают и грузы разлетаются под углом 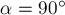
коэффициент упругости пружины. (МФТИ, 1992 г.)
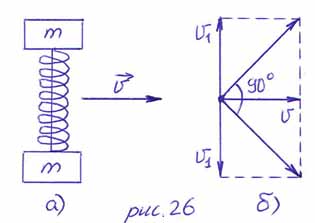
РЕШЕНИЕ. В системе
отсчёта, связанной с центром масс системы и движущейся в ту же сторону со
скоростью 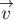
– разлетаются с одинаковыми скоростями 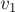
направлениях (по закону сохранения импульса системы тел). Таким образом
потенциальная энергия тел в поле упругих сил переходит в кинетическую энергию
тел. Так как в неподвижной системе отсчёта угол разлёта грузов равен 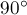
легко установить (рис. 26б), что 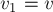
Пользуясь тем, что на систему
тел не действуют неконсервативные силы, запишем закон сохранения механической
энергии в системе отсчёта, связанной с центром масс:
Учитывая равенство модулей
скоростей 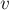
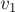
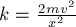
Взаимодействия тел, изучаемые в
механике, отличаются большим разнообразием. Одним из частных случаев таких
взаимодействий являются столкновения тел. Среди них выделяют так
называемые упругие и неупругие столкновения. Здесь мы будем называть
столкновения тел, при которых сохраняется суммарная механическая энергия тел, абсолютно
упругими (или просто упругими). Так, например, в большинстве случаев
можно считать абсолютно упругим центральное столкновение гладких стальных
шаров.
Столкновения, при которых
изменяется суммарная механическая энергия взаимодействующих тел, будем называть
неупругими. Изменение механической энергии при таких столкновениях
характеризуется, как правило, её убылью и сопровождается, например, выделением
теплоты. Причём количество выделившейся теплоты в точности равно убыли
суммарной механической энергии сталкивающихся тел. Если тела после столкновения
движутся как единое целое (с одинаковыми по модулю и направлению скоростями),
то такое столкновение будем называть абсолютно неупругим.
Кроме того, если на тела не
действуют внешние силы или они ограничены по модулю, то импульс системы тел при
столкновениях сохраняется, так как время столкновения, как правило, очень мало.
ПРИМЕР 31.
Гладкий шар,
движущийся со скоростью 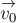
показано на рис. 28а. Определите скорости шаров после упругого столкновения.
РЕШЕНИЕ. Поскольку
скорость первого шара до соударения была направлена не по линии центров шаров,
то столкновение шаров – нецентральное. Направим ось 0х по линии центров
шаров в момент их столкновения. Ось 0у — перпендикулярно к ней (рис.
28б). Систему будем считать замкнутой.
Поскольку шары гладкие, то
покоящийся шар после столкновения полетит только в направлении оси 0х.
Пусть 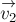
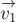
столкновения. Пусть проекции скорости 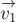
и 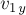
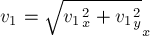
импульс системы шаров при столкновении сохраняется, то в проекциях на выбранные
оси координат имеем:
Поскольку столкновение упругое,
то суммарная механическая энергия шаров не изменяется:
Решая полученную систему
уравнений, находим: 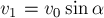
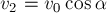
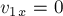
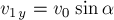
Из геометрии рисунка 28б
следует,
что
С учётом этого окончательно имеем: 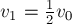

ПРИМЕР 32.
Шар
массой 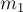
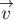
покоящийся шар массы 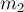
выделившейся теплоты после центрального абсолютно неупругого столкновения.
РЕШЕНИЕ. Поскольку
столкновение шаров абсолютно неупругое, то после него шары будут двигаться как
одно целое с некоторой скоростью 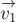
вдоль линии центров шаров в сторону движения.
Поскольку импульс системы шаров
сохраняется, то в проекциях на ось 0х имеем:
Убыль суммарной механической
энергии шаров равна количеству теплоты 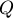
Решая полученную систему
уравнений, найдём:
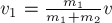
ПРИМЕР 33.
Лёгкий
пластилиновый шарик массы 
шарику со скоростью
Какое количество теплоты выделится при абсолютно неупругом
столкновении шарика с плитой? Массу плиты считать много большей массы шарика
( 
РЕШЕНИЕ. 1-й
способ решения.

Пусть 
плиты, 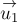
Направим ось 0х в сторону движения плиты, как показано на рис. 30.
Считая, что после столкновения плита с шариком движутся в том же направлении, в
котором двигалась плита до столкновения, по закону сохранения импульса можно
записать в проекциях на ось 0х уравнение:
Убыль суммарной механической
энергии плиты и шарика равна искомому количеству теплоты 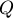
Решая полученную систему уравнений,
найдём 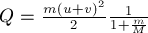
Учитывая, что по
условию 
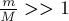
Пренебрегая столь малым
по сравнению с единицей отношением масс в знаменателе, получаем
окончательно 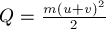
2-й способ решения.
Обратимся к записанному в
предыдущем способе решения уравнению закона сохранения импульса и выразим из
него скорость 
столкновения:
Преобразуем это выражение
следующим образом:
Учитывая, что по условию 
пренебрежём отношением 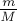
получим 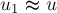
считать практически неизменной. И чем больше масса 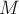
с 
скорость массивной плиты неизменной, перейдём в систему отсчёта, связанную с
плитой. В этой системе отсчёта плита покоится, а шарик до столкновения движется
навстречу плите со скоростью 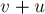
его кинетическая энергия равна
После столкновения в выбранной
системе отсчёта плита и шарик покоятся, их суммарная механическая энергия равна
нулю. Убыль механической энергии системы равна искомому количеству теплоты:
В начало
№15.
Работа силы. Работа потенциальных сил. Мощность. Энергия.

вводятся на основе понятия механической работы или работы силы.
Если на тело действует сила и тело под
действием этой силы перемещается, то говорят, что сила совершает работу.
Механическая работа – это скалярная величина, равная
произведению модуля силы, действующей на тело, на модуль перемещения и на
косинус угла между вектором силы и вектором перемещения (или скорости).
A = Fs cos α
Работа является скалярной величиной. Она
может быть как положительна (0° ≤ α < 90°), так и
отрицательна (90° < α ≤ 180°). При α = 90°
работа, совершаемая силой, равна нулю.
В системе СИ работа измеряется в джоулях
(Дж). Джоуль равен работе, совершаемой силой в 1 Н на перемещении
1 м в направлении действия силы.
[1 Дж=1 Н·м]
Работа силы, совершаемая в единицу
времени, называется мощностью. И характеризует быстроту выполнения
работы.
Мощность N – физическая величина,
равная отношению работы A к промежутку времени t, в течение которого совершена
эта работа:
N=A/t
В Международной системе (СИ) единица
мощности называется ватт (Вт). Ватт равен мощности силы,
совершающей работу в 1 Дж за время 1 с.
Внесистемная единица мощности 1 л.с.=735
Вт
Связь
между мощностью и скоростью при равномерном движении:
N=A/t так как A=FScosα
тогда N=(FScosα)/t, но S/t = v
следовательно
N=Fvcos α
В технике используются единицы работы и
мощности:
1 Вт·с = 1 Дж;
1Вт·ч = 3,6·103 Дж; 1кВт·ч =
3,6·106 Дж
Если тело способно совершить работу, то
говорят, что оно обладает энергией.
Механическая энергия тела – это скалярная величина, равная
максимальной работе, которая может быть совершена в данных условиях.
Обозначается Е Единица
энергии в СИ [1Дж = 1Н*м]
Механическая работа есть мера изменения
энергии в различных процессах А = ΔЕ.
Различают два вида механической энергии
– кинетическая Ек и потенциальная Еp энергия.
Полная механическая энергия тела равна
сумме его кинетической и потенциальной энергий
Е = Ек + Еp
Кинетическая энергия – это энергия тела, обусловленная
его движением.
Физическая величина, равная половине
произведения массы тела на квадрат его скорости, называется кинетической
энергией тела:
Кинетическая энергия – это энергия
движения. Кинетическая энергия тела массой m, движущегося со
скоростью равна работе,
которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить
ему эту скорость:
Если тело движется со скоростью , то для его полной
остановки необходимо совершить работу
Наряду с кинетической энергией или
энергией движения в физике важную роль играет понятие потенциальной энергии или энергии
взаимодействия тел.
Силы, работа которых не зависит от формы
траектории, а определяется начальным и конечным положением тела,
называются потенциальными.
Потенциальная энергия – энергия тела,
обусловленная взаимным расположением взаимодействующих между собой тел или
частей одного тела.
Понятие потенциальной энергии можно ввести
только для сил, работа которых не зависит от траектории движения тела и
определяется только начальным и конечным положениями. Такие силы
называются консервативными. Работа консервативных сил на
замкнутой траектории равна нулю.
Свойством консервативности обладают сила
тяжести и сила упругости. Для этих сил можно ввести
понятие потенциальной энергии.
Потенциальная энергия тела в поле силы
тяжести (потенциальная энергия тела, поднятого над землёй):
Ep = mgh
Она равна работе, которую совершает сила
тяжести при опускании тела на нулевой уровень.
Понятие потенциальной энергии можно ввести
и для упругой силы. Эта сила также обладает свойством
консервативности. Растягивая (или сжимая) пружину, мы можем делать это
различными способами.
Можно просто удлинить пружину на величину
x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и
т. д. Во всех этих случаях упругая сила совершает одну и ту же работу,
которая зависит только от удлинения пружины x в конечном состоянии, если
первоначально пружина была недеформирована. Эта работа равна работе внешней
силы A, взятой с противоположным знаком :
где k – жесткость пружины.
Растянутая (или сжатая) пружина способна
привести в движение прикрепленное к ней тело, то есть сообщить этому телу
кинетическую энергию. Следовательно, такая пружина обладает запасом энергии.
Потенциальной энергией пружины (или любого упруго деформированного тела)
называют величину
Потенциальная энергия упруго деформированного
тела равна
работе силы упругости при переходе из данного состояния в состояние с нулевой
деформацией.
Если в начальном состоянии пружина уже
была деформирована, а ее удлинение было равно x1, тогда при переходе в новое
состояние с удлинением x2 сила упругости совершит работу, равную изменению
потенциальной энергии, взятому с противоположным знаком:
Потенциальная энергия при упругой
деформации – это энергия взаимодействия отдельных частей тела между собой
силами упругости.
Если тела, составляющие замкнутую
механическую систему, взаимодействуют между собой только силами
тяготения и упругости, то работа этих сил равна изменению потенциальной энергии
тел, взятому с противоположным знаком:
A = –(Ep2 – Ep1).
По теореме о кинетической энергии эта работа
равна изменению кинетической энергии тел:
A = Ek2 – Ek1
Следовательно Ek2 – Ek1 = –(Ep2 – Ep1)
или Ek1 + Ep1 = Ek2 + Ep2.
Сумма кинетической и потенциальной
энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами
тяготения и силами упругости, остается неизменной.
Это утверждение выражает закон
сохранения энергии в механических процессах. Он является
следствием законов Ньютона.
Сумму E = Ek + Ep
называют полной механической энергией.
Полная механическая энергия замкнутой
системы тел, взаимодействующих между собой только консервативными силами, при
любых движениях этих тел не изменяется. Происходят лишь взаимные превращения
потенциальной энергии тел в их кинетическую энергию, и наоборот, или переход
энергии от одного тела к другому.
Е = Ек
+ Еp = const
Закон сохранения механической энергии
выполняется только тогда, когда тела в замкнутой системе взаимодействуют между
собой консервативными силами, то есть силами, для которых можно ввести понятие
потенциальной энергии.
В реальных условиях практически всегда на
движущиеся тела наряду с силами тяготения, силами упругости и другими
консервативными силами действуют силы трения или силы сопротивления среды.
Сила трения не является консервативной.
Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую
систему, действуют силы трения, то механическая энергия не сохраняется. Часть
механической энергии превращается во внутреннюю энергию тел (нагревание).
С развитием физики обнаруживались все
новые виды энергии: была обнаружена световая энергия, энергия
электромагнитных волн, химическая энергия, проявляющаяся при химических
реакциях (в качестве примера достаточно указать хотя бы на химическую энергию,
запасённую во взрывчатых веществах и превращающуюся в механическую и тепловую
энергию при взрыве), наконец, была открыта ядерная энергия.
Оказалось, что совершаемая над телом работа равна сумме всех видов
энергии тела; работа же, совершаемая некоторым телом над другими телами, равна убыли
суммарной энергии данного тела. Для всех видов энергии оказалось, что
возможен переход энергии из одного вида в другой, переход энергии от одного
тела к другому, но что при всех таких переходах общая энергия всех видов
остаётся все время строго постоянной. В этом заключается
всеобщность закона сохранения энергии.
Хотя общее количество энергии остается
постоянным, количество полезной для нас энергии может уменьшаться и в
действительности постоянно уменьшается. Переход энергии в другую форму может означать
переход ее в бесполезную для нас форму. В механике чаще всего это — нагревание
окружающей среды, трущихся поверхностей и т. п. Такие потери не только
невыгодны, но и вредно отзываются на самих механизмах; так, во избежание
перегревания приходится специально охлаждать трущиеся части механизмов.
Задачи
«Работа. Мощность. Энергия»
1. 
2 кг под действием силы F перемещается вверх по наклонной
плоскости на расстояние расстояние
тела от поверхности Земли при этом увеличивается на Вектор
силы направлен
параллельно наклонной плоскости, модуль силы F равен
30 Н. Какую работу при этом перемещении совершила сила F против
действия силы трения? Коэффициент трения
Решение. Работа силы
определяется как скалярное произведение вектора силы и вектора перемещения
тела. Сила трения связана с силой реакции опоры и коэффициентом трения
соотношением Согласно
второму закону Ньютона, где
—
угол наклона плоскости. Следовательно, сила трения при подъеме тела
вверх по наклонной плоскости совершила работу
2.Лебедка
равномерно поднимает груз массой 200 кг на высоту 3 м за 5 с.
Какова мощность двигателя лебедки?
Решение.
Поскольку
лебедка поднимает груз равномерно, по второму закону Ньютона, сила, с которой
тянет лебедка, в точности равна по модулю силе тяжести, действующей на груз.
Таким образом, лебедка совершает работу
Следовательно,
мощность двигателя лебедки равна
3.Под
действием силы тяги в 1 000 H автомобиль движется с постоянной
скоростью Какова
мощность двигателя? (Ответ дайте в кВт.)
Решение. Переведем
скорость в систему СИ: Мощность
двигателя связана со скоростью движения и силой тяги соотношением:
4.Какую
мощность развивает двигатель подъемного механизма крана, если он равномерно
поднимает плиту массой 600 кг на высоту 4 м за 3 с?
Решение.Кран работает
против силы тяжести. Поскольку груз поднимается равномерно, сила, с которой
тянет груз, равна по модулю силе тяжести, а значит груз совершает работу Таким
образом, мощность двигателя подъемного механизма крана равна :
5.
Кусок льда массой 2 кг упал без начальной скорости на землю с крыши высотой
5 м. Пренебрегая сопротивлением воздуха, определите среднюю мощность
силы тяжести, действовавшей на тело во время падения.
Решение. Работа силы
тяжести может быть вычислена по формуле:
Время падения тела
под действием ускорения свободного падения: Тогда
мощность:
6.Брусок
массой 5 кг равномерно перемещают по горизонтальной поверхности со скоростью 1
м/с, прикладывая к нему постоянную силу 4 Н, направленную под углом 60° к
горизонту. Чему равна мощность силы F?
Решение. Формула для
вычисления мощности силы:
7.Телу
массой 2 кг, находящемуся у основания шероховатой наклонной плоскости, сообщили
начальную скорость 3 м/с в направлении вверх вдоль наклонной плоскости.
Через некоторое время тело вернулось в исходную точку, имея втрое меньшую
кинетическую энергию. Какую работу совершила сила трения за время движения
тела?
Решение. По теореме о
кинетической энергии, изменение кинетической энергии равно работе внешних сил.
Единственной силой, совершающей работу, является сила трения.
Тогда:
8.Телу
массой 1 кг, находящемуся у основания шероховатой наклонной плоскости, сообщили
начальную скорость 2 м/с в направлении вверх вдоль наклонной плоскости.
Через некоторое время тело вернулось в исходную точку, имея вдвое меньшую
кинетическую энергию. Какую работу совершила сила трения за время движения
тела?
Решение. По теореме о
кинетической энергии, изменение кинетической энергии равно работе внешних сил.
Единственной силой, совершающей работу, является сила трения. Тогда:
9.Тело
массой 1 кг свободно падает на землю с высоты 20 м. Какую среднюю мощность
развивает сила тяжести за время падения тела?
Решение. Тело падает в
поле тяжести Земли, высота зависит от времени следующим образом

равна отношению работы, выполняемой за некоторый промежуток времени
10.Тело массой 0,5 кг
свободно падает на землю с высоты 80 м. Какую среднюю мощность развивает сила
тяжести за время падения тела?
Решение. Тело падает в
поле тяжести Земли, время падения связано с высотой следующим образом:

отношению работы, выполняемой за некоторый промежуток времени, к этому времени:
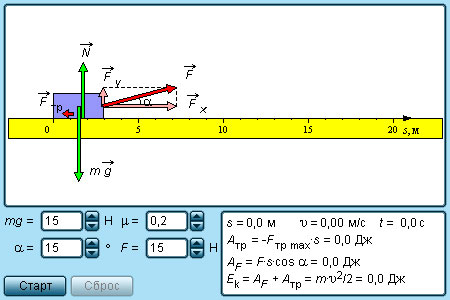
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Если действующая на тело сила вызывает его перемещение s, то действие этой силы характеризуется величиной, называемой механической работой (или, сокращенно, просто работой).
Механическая работа А — скалярная величина, равная произведению модуля силы F, действующей на тело, и модуля перемещения s, совершаемого телом в направлении действия этой силы.
Если направления перемещения тела и приложенный силы не совпадают, то работу можно вычислить как произведение модулей силы и перемещения, умноженному на косинус угла α между векторами силы и перемещения
(рис. 1.18.1):
Работа является скалярной величиной. Она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).
Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.
|
|
|
Рисунок 1.18.1. Работа силы |
Если проекция силы
на направление перемещения
не остается постоянной, работу следует вычислять для малых перемещений Δsi и суммировать результаты:
Это сумма в пределе (Δsi → 0) переходит в интеграл.
Графически работа определяется по площади криволинейной фигуры под графиком Fs(x) (рис. 1.18.2).
|
|
|
Рисунок 1.18.2. Графическое определение работы. ΔAi = FsiΔsi |
Примером силы, модуль которой зависит от координаты, может служить сила упругости пружины, подчиняющаяся закону Гука. Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу модуль которой пропорционален удлинению пружины (рис. 1.18.3).
|
|
|
Рисунок 1.18.3. Растянутая пружина. Направление внешней силы k – жесткость пружины. |
Зависимость модуля внешней силы от координаты x изображается на графике прямой линией (рис. 1.18.4).
|
|
|
Рисунок 1.18.4. Зависимость модуля внешней силы от координаты при растяжении пружины |
По площади треугольника на рис. 1.18.4 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:
Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы равна по модулю работе внешней силы
и противоположна ей по знаку.
Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами. При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил.
 |
|
Модель. Механическая работа. |
Мощность
Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.
В данной теме речь пойдёт о механической
работе и мощности.
Механическая работа — это скалярная физическая величина,
которая характеризует процесс перемещения тела под действием силы. Под
действием постоянной силы тело двигается прямолинейно и совершает перемещение в
направлении действия силы, то сила совершает работу, равную произведению модуля
этой силы и модуля перемещения.
Из определения следует единица
измерения работы в метрической системе единиц
Эта единица названа в честь
английского ученого Джеймса Прескотта Джоуля, впервые экспериментально
обосновавшего эквивалентность работы и теплоты.
Это самый простой случай,
когда перемещение тела и сила, действующая на него, совпадают по направлению.
Теперь рассмотрим, как
вычисляется работа, когда направление действия силы не совпадает с направлением
перемещения тела. Для этого рассмотрим следующий опыт. Через блок перекинута
нить на которой висит брусок некоторой массы. На брусок действуют две силы —
сила тяжести и сила натяжения нити.
Если равномерно тянуть за
нить, то тело будет равномерно двигаться, и, следовательно, результирующая
сила, действующая на тело, будет равна нулю.
Значит, при некотором
перемещении тела работа результирующей силы тоже будет равна нулю.
Однако сила натяжения нити совершает
работу.
Поскольку при равномерном
движении сила натяжения нити по модулю равна силе тяжести тела, то можно
предположить, что сила тяжести совершает такую же работу по величине, но
отрицательную.
Отсюда можно сделать вывод: работа
силы может быть положительной, отрицательной или равной нулю.
Заметим, что сила тяжести по
направлению противоположна перемещению тела. Это обстоятельство и другие
соображения позволяют предложить общую формулу для работы постоянной силы при
равномерном прямолинейном движении. Если вектор силы и перемещения составляют
между собой угол a, то работа этой силы равна
произведению модуля силы на модуль перемещения и на косинус угла между ними.
Это и есть общее выражение для
работы постоянной силы.
Из этой формулы видно, что в
случае, когда угол между направлением вектора силы и вектора перемещения
острый, то косинус этого угла будет больше нуля и, следовательно, больше
нуля будет работа силы.
Если вектор силы и вектор
перемещения составляют между собой тупой угол, то значение косинуса
этого угла меньше нуля. Значит и работа этой силы будет отрицательна.
И, наконец, если вектор
силы перпендикулярен вектору перемещения, то работа не
совершается (вернее, работа этой силы равна нулю).
Если к движущемуся телу
приложено несколько сил, то каждая из них совершает работу, а общая работа
равна алгебраической сумме работ, совершаемых отдельными силами.
Работу, совершенную силой, можно найти и графически.
Так, если действие силы на тело не меняется с течением времени и совпадает по
направлению с перемещением, то работа этой силы численно равна
площади заштрихованного прямоугольника.
Если же сила изменяется в
процессе движения, то работа этой силы тоже будет численно равна площади под
кривой. В частности, на рисунке представлен график силы, которая линейно
уменьшается с пройденным расстоянием до нуля. Очевидно, что работа этой силы
на пройденном пути, численно равна площади треугольника.
Ранее говорилось, что
основными силами в механике являются гравитационные силы (в частности сила
тяжести), силы упругости и силы трения.
Проанализируем более подробно работы,
совершаемые каждой из этих сил. Начнем с работы силы тяжести. Будем ее
рассматривать считая, что тело находится на небольших расстояниях от
поверхности Земли. В этом случае сила тяжести будет постоянной по модулю равной
Пусть тело массой m
падает с некоторой высоты h1 до
высоты h2. Тогда модуль
перемещения тела равен разности этих высот
Так как направления
перемещения и силы совпадают, то работа силы тяжести положительна и равна
произведению модуля силы тяжести и разности высот.
Следует помнить, что высоты,
на которых находится тело, можно отсчитывать от любого уровня. Это может быть
уровень поверхности Земли, пола или поверхности стола. Высоту выбранного уровня
принимают равной нулю. Поэтому этот уровень называют нулевым. Так, если тело
падает с высоты h до нулевого уровня, то работа силы тяжести равна
Теперь выясним, какую работу
совершает сила тяжести, если тело движется не по вертикали. Для этого
рассмотрим движение тела по наклонной плоскости.
Пусть тело некоторой массы m
совершило перемещение, равное по модулю длине наклонной плоскости. Работа силы
тяжести в этом случае равна
Из рисунка видно, что
Поэтому работа силы тяжести в
этом случае также равна
Таким образом, получили для
работы силы тяжести такое же выражение, как и в случае движения тела по
вертикали. Отсюда следует главный вывод о том, что работа силы тяжести не
зависит от того, по какой траектории движется тело и всегда равна произведению
модуля силы тяжести на разность высот в начальном и конечном положениях тела.
Тогда очевидно, что если
тело движется по замкнутой траектории, где начальное и конечное положения
тела совпадают, то работа силы тяжести равна нулю. Напомним, что такие
силы, работа которых не зависит от формы траектории, а определяется только
начальным и конечным положениями тела в пространстве, называются потенциальными
или консервативными. Следовательно, сила тяжести — это консервативная
сила.
Теперь проанализируем работу,
совершаемую силой упругости. Сила упругости — это сила, возникающая при
деформации тела внешними воздействиями.
Рассмотрим систему, состоящую
из пружины и тела некоторой массы, лежащего на достаточно гладкой
горизонтальной поверхности. Левый конец пружины прикреплен к стене, а правый —
к телу. Направим ось икс так, как показано на рисунке.
Если тело сместить на
некоторое расстояние от положения равновесия, то пружина будет действовать на
него с силой упругости, направленной вправо. Модуль проекции этой силы на ось Ox
будет определяться на основании закона Гука.
Теперь отпустим тело. Тогда
под действием силы упругости пружины тело будет смещаться вправо.
При этом сила упругости будет
совершать работу. Предположим, что тело переместилось так, что расстояние от
положения равновесия стало х2. Очевидно, что тогда модуль
перемещения тела равен разности между начальной и конечной координатой тела.
Для нахождения работы,
совершенной пружиной по перемещению тела, необходимо учесть, что сила упругости
меняется, так как ее величина зависит от удлинения пружины. Воспользуемся
графиком зависимости модуля силы упругости от удлинения пружины.
Известно, что работа силы
численно равна площади под графиком силы. В рассматриваемом
случае это площадь трапеции, основаниями которой являются силы упругости
пружины в положении один и два, а высота — это перемещение тела.
Из полученной формулы следует,
что работа силы упругости пружины зависит только от координат начального и
конечного положений. Из рисунка видно, что х1 и х2
— это и удлинение пружины, и координаты ее конца в выбранной системе координат.
Следовательно, работа силы упругости не зависит от формы траектории. А если
траектория замкнута, то работа равна нулю. Таким образом, сила упругости
является потенциальной силой.
И проанализируем работу,
совершаемую силой трения. Рассмотрим тело, находящееся на некоторой поверхности
(например, брусок на поверхности стола).
Если толкнуть брусок, то он
придет в движение, однако, через некоторое время, остановится. В процессе
движения бруска на него действуют: сила тяжести, сила нормальной реакции опоры
и сила трения скольжения. Под действием этих трех сил и движется брусок.
Поскольку сила тяжести компенсируется силой нормальной реакции стола, то
равнодействующая сила равна действующей на брусок силе трения. А так как сила
трения направлена противоположна перемещению, то работа этой силы будет
отрицательной (так как косинус ста восьмидесяти градусов равен минус единице).
Из формулы следует, что работа
силы трения зависит от модуля перемещения тела. И даже если тело
вернется в исходную точку, то работа силы трения не будет равна нулю.
Такие силы, работа которых зависит от формы траектории движения тела и на
замкнутой траектории отличны от нуля, называются непотенциальными или диссипативными
(от латинского — рассеяние).
Однако не надо думать, что
работа сил трения всегда отрицательна. Ведь именно благодаря силе трения покоя
человек и различные машины движутся по Земле. Действительно, при ходьбе человек
действует на поверхность Земли с некоторой силой F1 (кроме силы нормальной реакции), а по третьему закону
Ньютона Земля действует на ногу человека с силой трения покоя, равной по модулю
силе воздействия человека, но противоположно направленной. Благодаря этой силе
человек движется. Сила трения покоя направлена также, как и скорость человека,
и, следовательно, работа этой силы положительна.
Таки образом, были рассмотрены
работы основных трех сил, с которыми чаще всего мы сталкиваемся в механике.
Однако, одна и та же работа в разных случаях может быть выполнена за различные
промежутки времени, то есть она может совершаться неодинаково быстро. Очевидно,
что чем меньшее времени требуется для выполнения данной работы, тем эффективнее
работает машина, механизм и прочее.
Величина, характеризующая
быстроту совершения работы, и равная отношению работы, совершаемой силой, к
промежутку времени, в течение которого она совершается, называется мощностью.
Исходя из определения видим,
что единицей измерения мощности является
Эта единица получила название Ватт,
в честь английского ученого Джеймса Уатта — изобретателя универсального
парового двигателя.
При движении любого тела на
него в общем случае действует несколько сил, каждая из которых совершает работу
и, следовательно, для каждой силы можно вычислить мощность. Так, если тело
движется прямолинейно и на него действует постоянная сила, то она совершает
работу, равную
Тогда мощность силы равна
отношению работы этой силы к промежутку времени.
Мощность силы также равна
произведению модуля силы на модуль скорости и на косинус угла между
направлениями вектора силы и вектора скорости.
По записанной формуле можно
рассчитывать и среднюю, и мгновенную мощности, подставляя значение средней или
мгновенной скорости.
Из полученной формулы следует,
что при заданной мощности мотора сила тяги тем меньше, чем больше скорость
движения. Вот почему водители автомобилей при подъеме в гору, когда нужна
наибольшая сила тяги, переключают двигатель на пониженную передачу.
И так, любой двигатель
или механическое устройство предназначены для выполнения определенной механической работы.
Эта работа называется полезной работой. Для двигателя автомобиля
— это работа по его перемещению, для токарного станка — работа по вытачиванию
детали.
Однако в любой машине, в
любом двигателе полезная работа всегда меньше той энергии, которая
затрачивается для приведения их в действие, потому что всегда существуют
силы трения, работа которых приводит к нагреванию каких-либо частей устройства.
А нагревание нельзя считать полезным результатом действия машины. Поэтому
каждое устройство характеризуется особой величиной, которая показывает,
насколько эффективно используется подводимая к нему энергия. Эта величина
называется коэффициентом полезного действия и обычно обозначается
греческой буквой h.
И так, коэффициентом
полезного действия называется отношение полезной работы, совершенной
машиной за некоторый промежуток времени, ко всей затраченной работе (или
подведенной энергии) за тот же промежуток времени.
Коэффициент полезного действия
обычно выражается в процентах. Поскольку и полезную, и затраченную работы можно
представить, как произведение мощности на промежуток времени в течение которого
работала машина, то
Основные выводы:
Рассмотрели важную физическую величины
– работу. Рассмотрели работы наиболее
часто встречающихся сил — силы тяжести, упругости и силы трения. Повторили
понятие мощности, а также вспомнили, что называют коэффициентом полезного
действия механизма.
| Работа | |
 |
|
| Размерность |
L2MT−2 |
|---|---|
| Единицы измерения | |
| СИ |
Дж |
| СГС |
эрг |
| Примечания | |
|
скалярная величина |
| |
||||||
|
|
||||||
| Работа силы | ||||||
| Ключевые статьи | ||||||
|
||||||
| См. также: Портал:Физика |
Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы[1].
Содержание
- 1 Определение
- 1.1 Работа силы (сил) над одной точкой
- 1.2 Работа силы (сил) над системой или неточечным телом
- 2 Кинетическая энергия
- 3 Потенциальная энергия
- 4 Работа в термодинамике
- 5 Работа силы в теоретической механике
- 6 Размерность и единицы
- 7 Ссылки
- 8 Литература
- 9 См. также
Определение
В механике можно ввести понятие работы, исходя из довольно простых представлений[2]
Работа силы (сил) над одной точкой
- Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.
При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения[3]:
Здесь точкой обозначено скалярное произведение[4], 

Если сила не постоянна, то в этом случае она вычисляется как интеграл[5]:
(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений 
Если существует зависимость силы от координат[6], интеграл определяется[7] следующим образом:
,
где 

- Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.
Работа силы (сил) над системой или неточечным телом
Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой).
Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.
- Эти определения могут быть использованы как для какой-то конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.
Кинетическая энергия
Кинетическая энергия вводится в механике в прямой связи с понятием работы.
Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).
Если 
где 

Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.
Потенциальная энергия
Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая 
Если все силы, действующие на частицу консервативны, и 
 . . |
Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы
является постоянной относительно времени. Этот закон широко используется при решении задач классической механики.
Работа в термодинамике
В термодинамике работа, совершенная газом при расширении[8], рассчитывается как интеграл давления по объёму:
Работа, совершенная над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.
- Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объема, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
- В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).
Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет
Видно, что это и есть произведение давления на приращение объема вблизи данной элементарной площадкой. А просуммировав по всем dS получим конечный результат, где будет уже полное приращение объема, как и в главной формуле параграфа.
Работа силы в теоретической механике
Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.
Пусть материальная точка 











В соответствии с определением интеграла Римана, можем дать определение работе:
Предел, к которому стремится сумма 




Таким образом, если обозначить эту работу буквой 
,
следовательно,
(1).
Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра 


Размерность и единицы
Единицей измерения работы в СИ является Джоуль, в СГС — эрг
- 1 Дж = 1 кг·м²/с² = 1 Н·м
- 1 эрг = 1 г·см²/с² = 1 дин·см
- 1 эрг = 10−7 Дж
Ссылки
- ↑ Концепции современного естествознания
- ↑ Такие представления можно конкретизировать как систему постулатов, приводящую достаточно однозначно к определению, описанному в основной статье:
- работу совершает только компонента силы, совпадающая с направлением перемещения точки, к которой она приложена, или противоположная направлению перемещения точки (в последнем случае работа считается отрицательной),
- работа постоянной силы пропорциональна компоненте такой силы, описанной в пункте 1, и длине вектора перемещения,
- работа по перемещению точки за несколько последовательных промежутков времени суммируется (работа за всё это время равна сумме работ, совершенных за каждый промежуток),
- работа суммы (векторной суммы) сил, приложенных к точке равна сумме работ, совершенных каждой силой в отдельности,
- работа, совершенная над системой (телом) равна сумме работ, совершенных над каждой ее частью (в частности — равна сумме работ, совершенных над каждой точкой системы).
- ↑ Механическая работа. Мощность
- ↑ Можно считать, что механическая работа может служить в области физики одной из главных иллюстраций для скалярного произведения.
- ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения
, на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях
суммируется, что и дает в результате интеграл.
- ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
- ↑ По сути через предыдущий, поскольку здесь
; вектор же малого перемещения
совпадает с
.
- ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле
давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить ее к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).
Литература
- Кудрявцев Л. Д. Курс математического анализа. — 5-е, переработанное и дополненное. — М.: Дрофа, 2003. — Т. 1. — С. 640—641. — 703 с.
См. также
- Закон сохранения энергии
- Механические приложения криволинейных интегралов



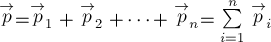
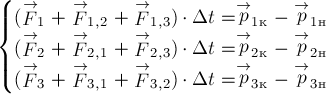
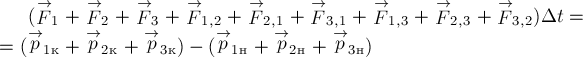
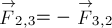
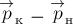
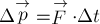
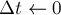 ), а равнодействующая всех сил, действующих
), а равнодействующая всех сил, действующих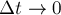 ), а алгебраическая сумма
), а алгебраическая сумма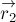
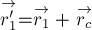
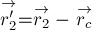
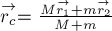
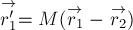
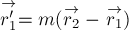
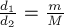
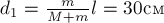
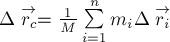
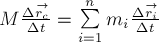
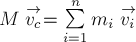
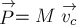
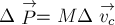
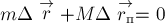
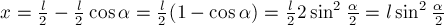
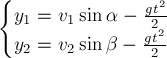
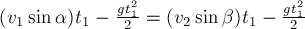
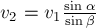
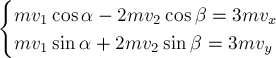
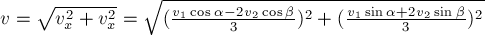
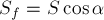
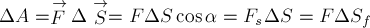
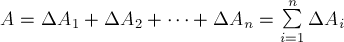
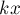
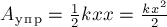
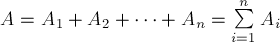
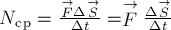
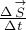
![[N] = frac {[A]}{[{Delta} t]} = [F] [v] = кг м^2/c^2](http://mipt-bot.narod.ru/cache/tex/18eacc97f673a4d0baa53f7665eb8335.png)
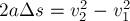
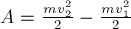
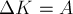
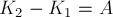
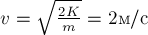
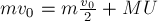
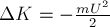
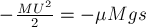
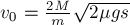
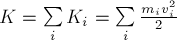
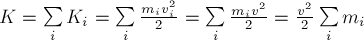
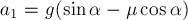
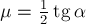
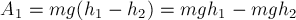
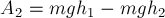
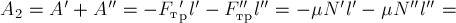
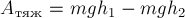
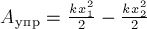
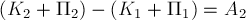
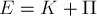
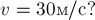
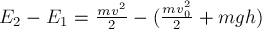
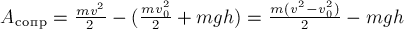
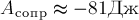
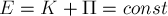
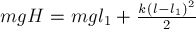
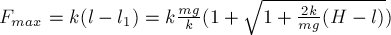
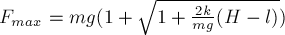
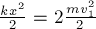
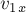
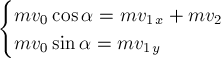
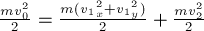
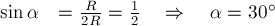
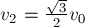
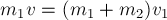
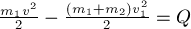
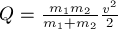
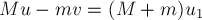
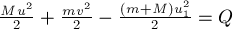
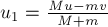
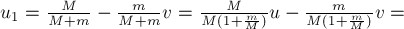
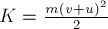
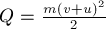





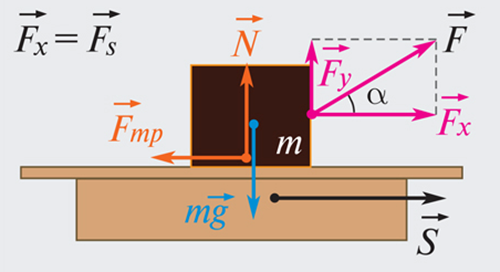
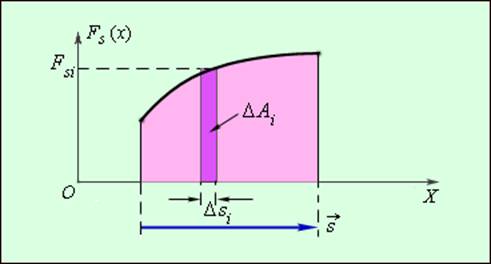
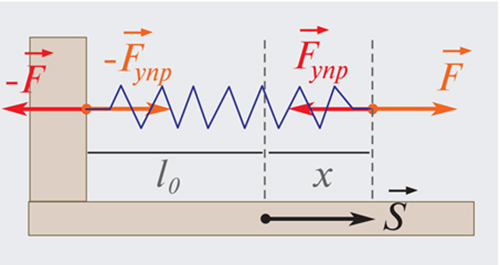
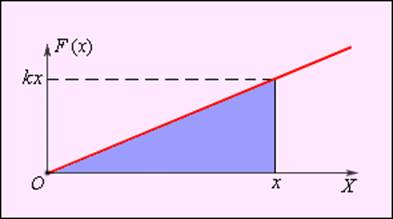
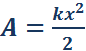

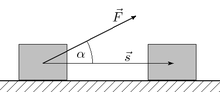


 ,
,





 ,
, (1).
(1).![W=intlimits_a ^b F[s(t)]s'(t)dt.](https://dic.academic.ru/dic.nsf/ruwiki/aac543b76b4a47af3ceecb90c8f18e3e.png)
 , на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях
, на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях  ; вектор же малого перемещения
; вектор же малого перемещения  .
. давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить ее к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).
давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить ее к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).


