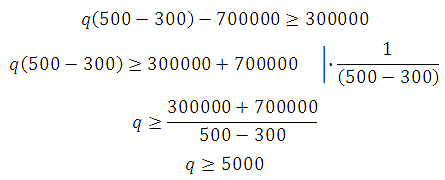Некоторая компания продает свою продукцию по цене p 700 руб за единицу 300 500000

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

4 января 2012

Линейные уравнения — простейшие конструкции, которые изучаются в школьном курсе математики. Многие задачи B12, которые встречаются в ЕГЭ и выглядят достаточно угрожающе, в итоге сводятся к этим самым линейным уравнениям.

Как правило, линейные уравнения возникают, если:

1. При подстановке переменных в исходную формулу задачи сводится к пропорции. В этом случае достаточно вспомнить основное свойство пропорции — умножение «крест-накрест» — и мы получим классическое линейное уравнение;
2. Формула изначально была линейной. Достаточно редкий случай. Думаю, тут все понятно: записываем уравнение, решаем, находим ответ.

В любом случае, помните основное правило, одинаково полезное для решения всех задач B12:

Избавляйтесь от дробей и отрицательных степеней в формулах. Если можно умножить — умножайте; можно сократить — сокращайте. Дроби (особенно десятичные) можно записывать только в ответе.

Многие, кто впервые слышит это правило, начинают возмущаться. Мол, к чему такие сложности? Ведь это дополнительные действия, в которых можно допустить еще больше ошибок!

Но статистика неумолима: число ошибок, связанных с преобразованием дробей, меркнет по сравнению с огромным множеством ошибок, которые возникают:

1. Из-за дробных коэффициентов в уравнениях;
2. При умножении степеней с отрицательными показателями;
3. Как ни странно, при сложении и вычитании обыкновенных дробей.

Отдельная проблема — переход от правильной дроби к неправильной и обратно. Подобные операции встречаются во многих задачах ЕГЭ по математике, поэтому настоятельно рекомендую изучить их (см. урок «Что такое числовая дробь»).

В общем, следуйте приведенному выше правилу и не допускайте глупых ошибок. А сейчас посмотрим, как это работает, на конкретных экзаменационных задачах.

Задача. Некоторая компания продает свою продукцию по цене p = 700 руб. за единицу, переменные затраты на производство одной единицы продукции составляют v = 400 руб., постоянные расходы предприятия f = 800 000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле:

π (q) = q(p − v) − f.

Определите наименьший месячный объем производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 1 000 000 руб.

Классическая задача на подстановку переменных в формулу. По условию, нам известно следующее:

π (q) = q(p − v) − f; p = 700; v = 400; f = 800 000.

Требуется, чтобы месячная операционная прибыль π (q) = 1 000 000. Подставляем значения переменных p, v и f в формулу и решаем уравнение:

1 000 000 = q(700 − 400) − 800 000;
1 000 000 + 800 000 = q · 300;
300q = 1 800 000;
q = 6000.

Итак, для получения требуемой месячной прибыли необходимо производить 6000 единиц продукции в месяц — это и есть ответ.

Задача. Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома:

где U — напряжение в вольтах, R — сопротивление электроприбора в Омах.

В электросеть включен предохранитель, который плавится, если сила тока превышает 11 А. Определите, какое минимальное сопротивление (в Омах) должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать.

Избавимся от дробей в формуле, переписав ее в виде I · R = U. Далее подставим в эту формулу известные величины: силу тока I = 11 и напряжение U = 220 (единицы измерения писать не надо). Имеем:

11 · R = 220 ⇒ R = 20.

Итак, сопротивление электроприбора должно быть не менее 20 Ом — это и есть ответ.

Задача. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой:

где T₁ — температура нагревателя (в градусах Кельвина), T₂ — температура холодильника (в градусах Кельвина).

При какой минимальной температуре нагревателя T₁ КПД этого двигателя будет не меньше 35%, если температура холодильника T₂ = 260 К? Ответ выразите в градусах Кельвина.

Снова избавляемся от дроби в формуле. Получим:

η · T₁ = (T₁ − T₂) · 100%

Теперь решаем задачу. Нам известны КПД двигателя η = 35 и температура холодильника T₂ = 260. Единицы измерения писать не надо, т.к. по условию все числа уже приведены в СИ. Имеем:

35 · T₁ = (T₁ − 260) · 100;
35T₁ = 100T₁ − 26 000 — раскрыли скобки;
26 000 = 100T₁ − 35T₁;
26 000 = 65T₁;
T₁ = 400 — это ответ.

Задача. При температуре 0 °C рельс имеет длину l₀ = 15 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону:

l(t°) = l₀(1 + α · t°)

где α = 1,2 · 10⁻⁵ (°C)⁻¹ — коэффициент теплового расширения, t° — температура (в градусах Цельсия). При какой температуре рельс удлинится на 6,3 мм? Ответ выразите в градусах Цельсия.

Довольно зверская задача, поскольку и формула, и числа в ней весьма сложные. Для начала выясним, что означает фраза «рельс удлинится на 6,3 мм». Итак, был рельс длиной 15 метров. Затем рельс удлинился на 6,3 мм = 6,3 · 10⁻³ метра (т.к. 1 мм — это 10⁻³ метра), и теперь общая длина равна 15 + 6,3 · 10⁻³ метра.

Теперь, когда мы разобрались, что значит «рельс удлинится», можно решить задачу. Имеем: l₀ = 15; l(t°) = 15 + 6,3 · 10⁻³; α = 1,2 · 10⁻⁵. Подставляем в исходную формулу — получаем:

15 + 6,3 · 10⁻³ = 15 · (1 + 1,2 · 10⁻⁵ · t);
15 + 6,3 · 10⁻³ = 15 + 15 · 1,2 · 10⁻⁵ · t — раскрыли скобки;
6,3 · 10⁻³ = 18 · 10⁻⁵ · t — убрали 15 с обеих сторон;
6,3 · 10⁻³ · 10⁵ = 18 · 10⁻⁵ · 10⁵ · t — умножили все на 10⁵;
6,3 · 10² = 18 · t — избавились от отрицательных степеней;
18t = 630 — получили нормальное уравнение;
t = 35 — решили уравнение.

Как видите, при аккуратном подходе даже самые сложные задачи (например, с рельсами) решаются быстро.

В заключение — небольшое замечание касательно единиц измерения. Вопрос: когда их надо преобразовывать, а когда на это можно забить? В ЕГЭ по математике существует лишь две потенциально «опасные» величины:

1. Скорость. Может измеряться в метрах в секунду, а может — в километрах в час;
2. Расстояние. В разных задачах измеряется в метрах, километрах и даже миллиметрах (как в случае с рельсами).

Остальные числа — время, температура и другие физические величины — всегда даются в СИ. Исключения существуют, но их единицы, и такие задачи сразу бросаются в глаза.

Смотрите также:

1. Решение задач B12: №440—447
2. Работа с формулами в задаче B12
3. Сложные выражения с дробями. Порядок действий
4. Сводный тест по задачам B15 (2 вариант)
5. Учимся расщеплять ответы в тригонометрических уравнениях
6. Задача B4: транзит нефти

Компания продает свою продукцию по цене…

Дата: 2014-09-15

5193

Категория: Физические задачи

Метка: ЕГЭ-№8

27954. Компания продает свою продукцию по цене p = 500 рублей. за единицу, переменные затраты на производство одной единицы продукции составляют      v = 300 рублей, постоянные расходы предприятия f = 700000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле п(q)=q(p–v)–f. Определите наименьший месячный объем производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300000 руб.  

Выражение «не меньше 300000 рублей» означает, что месячная операционная прибыль предприятия будет равна или больше 300000 рублей, то есть

п(q)= q≥ 300000.

Задача сводится к решению неравенства q(p–v)–f≥300000, где необходимо найти  q.

Подставим  известные величины:  

5000 единиц продукции это наименьший объем производства, при котором месячная операционная прибыль предприятия будет не меньше 300000 руб.

Данную задачу можно также решить, составив уравнение:

Так как понятно, что при наименьшем объёме производства будет наименьшая прибыль.  

Ответ: 5000

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Ok

На этой странице сайта, в категории Математика размещен ответ на вопрос
Некоторая компания продаёт свою продукцию по цене p = 500 руб?. По уровню сложности вопрос рассчитан на учащихся
5 — 9 классов. Чтобы получить дополнительную информацию по
интересующей теме, воспользуйтесь автоматическим поиском в этой же категории,
чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы
расположена кнопка, с помощью которой можно сформулировать новый вопрос,
который наиболее полно отвечает критериям поиска. Удобный интерфейс
позволяет обсудить интересующую тему с посетителями в комментариях.