Компания выбирает место для строительства торгово‐развлекательного комплекса: на месте квартала старых одноэтажных домов в центре города или на окраине города. Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется сдавать 4000 м2 площади комплекса. Стоимость земли, цена строительства комплекса с учётом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.
| Место | Цена земли (млн руб.) |
Цена строительства (млн руб.) |
Длина коммуникаций (м) |
Стоимость аренды за 1 м2 (руб./месяц) |
|---|---|---|---|---|
| Центр | 64,4 | 176 | 200 | 1200 |
| Окраина | 11,2 | 168 | 3500 | 900 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций? Ответ округлите до целых.
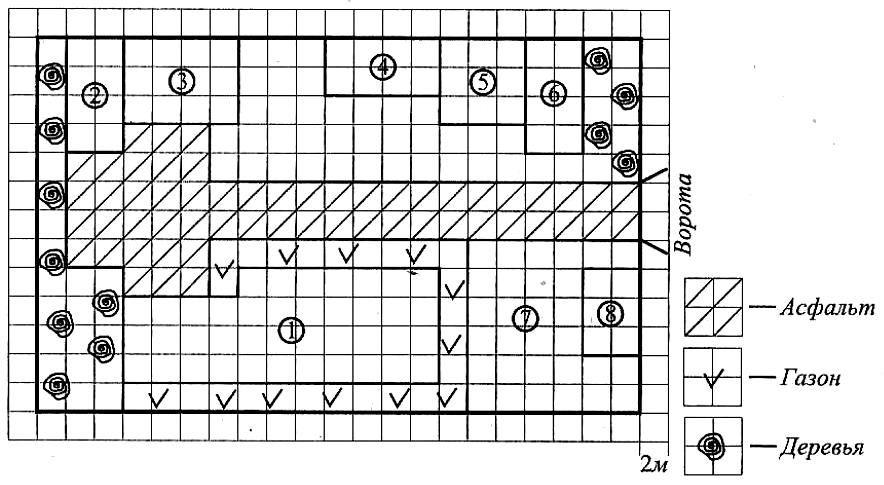
На плане (см. рис.) изображён район города, в котором живёт Петя. Сторона каждой клетки на плане равна 10 м.
Дом, в котором живёт Петя, обозначен цифрой 6. Прямо напротив дома, где живёт Петя, через дорогу находится дом в форме буквы «Г», где живёт его друг Вася. Рядом с домом, где живёт Петя, расположен дом, где живёт одноклассница Таня, а напротив него через дорогу имеется здание банка площадью 600 м2. А с другой стороны дома, где живёт Таня, расположен детский сад. Недалеко от детского сада и дома, где живёт Петя, находится магазин. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах от неё — квартал старых одноэтажных домов.
1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Банк | Магазин | Дом, где живёт Таня |
Квартал старых домов |
|---|---|---|---|---|
| Цифры |
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
2
Территорию стадиона необходимо засеять газонной травой. В одной упаковке газонной травы содержится 12 кг семян, при этом для засеивания 3 м2 земли необходимо 100 г семян. Какое минимальное количество упаковок газонной травы необходимо приобрести?
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
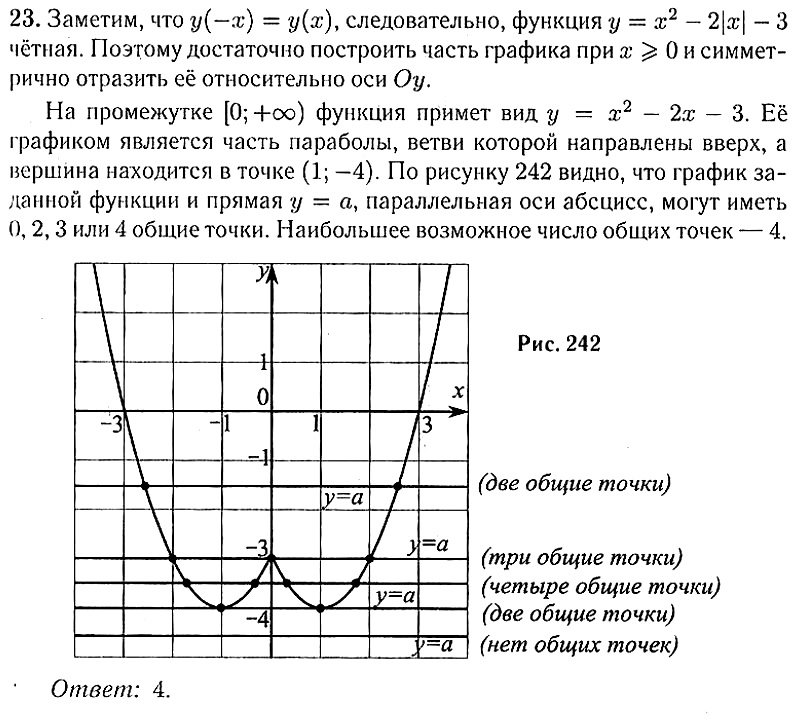
3
Найдите суммарную площадь, которую занимают дома, где проживают Таня, Петя и Вася. Ответ дайте в м2.
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
4
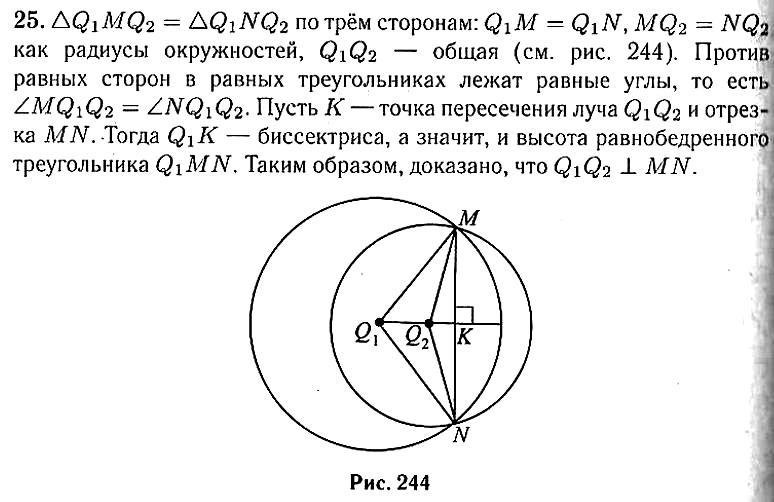
Найдите расстояние от дома, где живёт Петя, до автобусной остановки (расстояние между двумя ближайшими точками по прямой) в метрах.
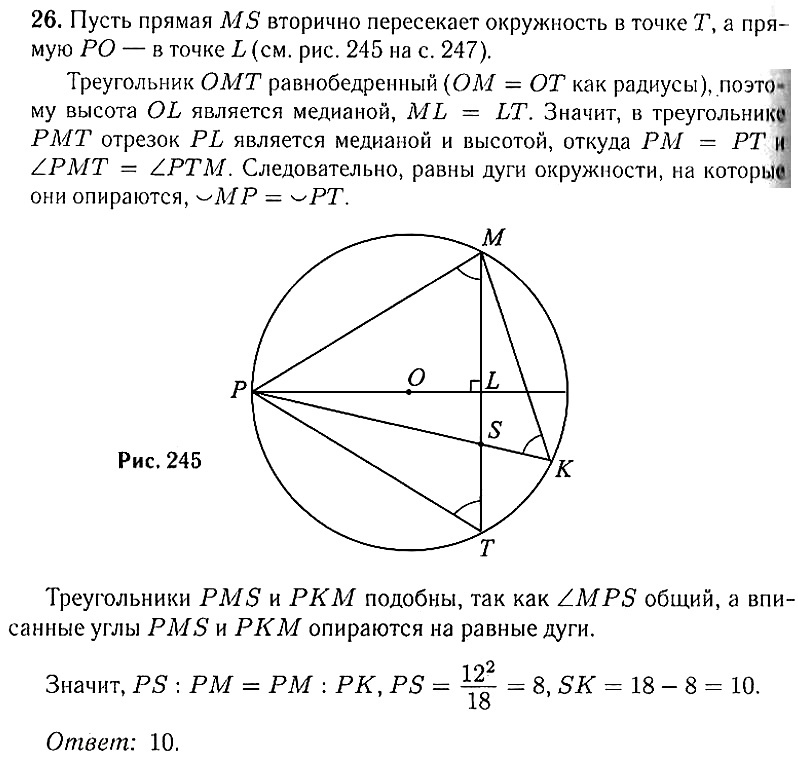
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
Спрятать решение
Решение.
Стоимость постройки ТРК в центре города равна
рублей.
Стоимость постройки ТРК на окраине города равна
рублей.
Разница в стоимости составляет
рублей.
Разница в стоимости аренды составляет
рублей.
Значит, более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций через месяцев. Округляя, получаем ответ — 35 месяцев.
Ответ: 35.
Источник: Тренировочный вариант № 231, усложнённая версия, Александр Ларин
ОГЭ математика
126 вариант
1. Для объектов, указанных в таблице, определите, какими цифрами они
обозначены на схеме. Заполните таблицу, в ответ запишите последовательность
четырёх цифр.
|
Объекты |
Магазин |
Фитнес‐центр |
Мастерская |
Дом, где |
|
Цифры |
На плане (см. рисунок) изображён район города, в котором проживает
Вика. Сторона каждой клетки на плане равна 15 м. Рядом с домом Вики,
обозначенным на плане цифрой 4, находится одноэтажный магазин площадью
900 м2 и фитнес‐центр. В 15 м от магазина расположен
дом, где живёт одноклассник Вики Артём. В 30 м от детской площадки
находится дом, где живёт Олег. Если выйти из фитнес‐центра, пройти
небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к
угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по
ремонту бытовой техники. Через дорогу от дома дедушки расположен рынок, а
недалеко от него – мебельный центр площадью 2025 м2.
2. Детскую площадку решили покрыть резиновой плиткой размером
1 м × 1 м каждая. Плитка продаётся упаковками по 16 штук. Какое минимальное
количество упаковок плитки необходимо приобрести?
3. Найдите суммарную площадь, которую занимают магазин и
фитнес-центр. Ответ дайте в м2.
4. По периметру детской площадки планируется поставить забор. Найдите
его длину (в метрах).
5. Фирма выбирает место для строительства гостиницы: в центре города
или на его окраине. Стоимость прокладки 1 метра коммуникаций равна 5500 рублей.
В гостинице планируется сдавать 500 номеров. Стоимость земли, цена
строительства гостиницы и средняя стоимость номера даны в таблице.
|
Место |
Цена земли |
Цена |
Длина |
Стоимость |
|
Центр |
58,2 |
136 |
200 |
3200 |
|
Окраина |
11,3 |
128 |
2800 |
2800 |
Обдумав оба варианта, компания выбрала местом для строительства
центр города. Через сколько суток после начала сдачи номеров (при условии
полной загрузки гостиницы) более высокая стоимость номеров компенсирует
разность в стоимости земли, строительства и прокладывания коммуникаций?
6. Найдите значение выражения
7. На координатной прямой отмечены числа r, q и p.
Какая из разностей q − p, q − r, r − p положительна?
В
ответе укажите номер правильного варианта.
1) q − p
2) q − r
3) r − p
4) ни одна из них
8. Найдите значение выражения при
9. Решите уравнение .
10. Девятиклассники Петя, Катя, Ваня, Даша и Наташа бросили жребий,
кому начинать игру. Найдите вероятность того, что начинать игру должен будет
мальчик.
11. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)
Б)
B)
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
12. Радиус описанной около треугольника окружности можно найти по
формуле , где
—
сторона треугольника, — противолежащий этой стороне
угол, а — радиус описанной около этого треугольника окружности. Пользуясь этой
формулой, найдите , если
, а
.
13. Укажите решение неравенства
1)
2)
3)
4)
14. При свободном падении тело прошло в первую секунду 5 м, а в каждую
следующую на 10 м больше. Найдите глубину шахты, если свободно падающее тело
достигло его дна через 5 с после начала падения.
15.
Найдите острый угол параллелограмма , если биссектриса
угла образует со стороной
угол, равный 41°. Ответ дайте в
градусах.
16. 
окружности равна 72, а расстояние от центра окружности до этой хорды равно 27.
Найдите диаметр окружности.
17. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
18.
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный
треугольник. Найдите длину его большего катета.
19. Какие из следующих утверждений верны?
1. Через точку, не лежащую на данной прямой, можно провести
прямую, параллельную этой прямой.
2. В тупоугольном треугольнике все углы тупые.
3. Любой квадрат является прямоугольником.
В
ответ запишите номера выбранных утверждений без пробелов, запятых и других
дополнительных символов.
20. Найдите значение выражения если
21. Из городов А и В навстречу друг другу одновременно выехали
мотоциклист и велосипедист. Мотоциклист приехал в В на 42 минуты раньше, чем
велосипедист приехал в А, а встретились они через 28 минут после выезда.
Сколько часов затратил на путь из В в А велосипедист?
22. Найдите все значения , при которых неравенство
не имеет
решений.
23.
Найдите угол АСО, если его сторона СА касается
окружности, О — центр окружности, а дуга AD окружности,
заключённая внутри этого угла, равна 100°
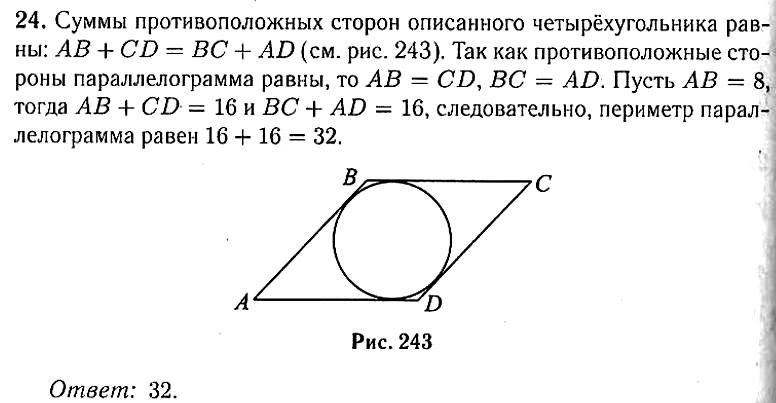
24. В параллелограмме ABCD диагонали AC и BD пересекаются
в точке K. Докажите, что площадь параллелограмма ABCD в
четыре раза больше площади треугольника AKB.
25. На стороне BC остроугольного треугольника ABC (AB≠AC)
как на диаметре построена полуокружность, пересекающая высоту AD в
точке M, AD = 15, MD = 3, H —
точка пересечения высот треугольника ABC. Найдите AH.
Решение
1. Для объектов, указанных в таблице, определите, какими цифрами они
обозначены на схеме. Заполните таблицу, в ответ запишите последовательность
четырёх цифр.
|
Объекты |
Магазин |
Фитнес‐центр |
Мастерская |
Дом, где |
|
Цифры |
На плане (см. рисунок) изображён район города, в котором проживает
Вика. Сторона каждой клетки на плане равна 15 м. Рядом с домом Вики,
обозначенным на плане цифрой 4, находится одноэтажный магазин площадью
900 м2 и фитнес‐центр. В 15 м от магазина расположен
дом, где живёт одноклассник Вики Артём. В 30 м от детской площадки
находится дом, где живёт Олег. Если выйти из фитнес‐центра, пройти
небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к
угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по
ремонту бытовой техники. Через дорогу от дома дедушки расположен рынок, а
недалеко от него – мебельный центр площадью 2025 м2.
Решение.
Рядом с домом Вики, обозначенным на плане цифрой 4, находится
одноэтажный магазин площадью 900 м2 и фитнес‐центр. Значит,
магазин отмечен цифрой 7, а фитнес-центр — цифрой 5. 30 м от детской площадки
находится дом, где живёт Олег. Следовательно, дом, где живёт Олег, обозначен
цифрой 1. Если выйти из фитнес‐центра, пройти небольшой ельник, обозначенный цифрой 6, и детскую
площадку, то приходишь к угловому дому, где живёт дедушка Вики. Рядом с ним
находится мастерская по ремонту бытовой техники. Значит, мастерская отмечена
цифрой 2.
Ответ: 7521.
2. Детскую площадку решили покрыть резиновой плиткой размером
1 м × 1 м каждая. Плитка продаётся упаковками по 16 штук. Какое минимальное
количество упаковок плитки необходимо приобрести?
Решение.
Найдём площадь детской площадки:
м2.
Одна плитка имеет площадь 1 м2. Значит,
потребуется упаковок плитки.
Таким образом, необходимо приобрести 352 упаковки плитки.
Ответ: 352.
3. Найдите суммарную площадь, которую занимают магазин и
фитнес-центр. Ответ дайте в м2.
Решение.
Площадь, которую занимают магазин и фитнес-центр, равна
м2.
Ответ: 2700.
4. По периметру детской площадки планируется поставить забор. Найдите
его длину (в метрах).
Решение.
Найдём периметр детской площадки — это сумма длин четырех сторон,
по 5 клеток каждая:
м.
Ответ: 300.
5. Фирма выбирает место для строительства гостиницы: в центре города
или на его окраине. Стоимость прокладки 1 метра коммуникаций равна 5500 рублей.
В гостинице планируется сдавать 500 номеров. Стоимость земли, цена
строительства гостиницы и средняя стоимость номера даны в таблице.
|
Место |
Цена земли |
Цена |
Длина |
Стоимость |
|
Центр |
58,2 |
136 |
200 |
3200 |
|
Окраина |
11,3 |
128 |
2800 |
2800 |
Обдумав оба варианта, компания выбрала местом для строительства
центр города. Через сколько суток после начала сдачи номеров (при условии
полной загрузки гостиницы) более высокая стоимость номеров компенсирует
разность в стоимости земли, строительства и прокладывания коммуникаций?
Решение.
Стоимость постройки гостиницы в центре города равна
рублей.
Стоимость постройки гостиницы на окраине города равна
рублей.
Разница в стоимости составляет
рублей.
Разница в стоимости номера составляет
рублей.
Значит, более высокая стоимость номеров компенсирует разность в
стоимости земли, строительства и прокладывания коммуникаций через дня.
Ответ: 203.
6. Найдите значение выражения
Решение.
Вычислим:
Ответ: 5,25.
7. На координатной прямой отмечены числа r, q и p.
Какая из разностей q − p, q − r, r − p положительна?
В
ответе укажите номер правильного варианта.
1) q − p
2) q − r
3) r − p
4) ни одна из них
Решение.
Заметим, что r < q < p. Разность
положительна только в том случае, когда вычитаемое меньше уменьшаемого. Это
верно только для разности q − r.
Правильный ответ указан под номером: 2.
8. Найдите значение выражения при
Решение.
Упростим выражение
Подставим значения :
Ответ: -60
9. Решите уравнение .
Решение.
Умножим уравнение на 7, получим:
10. Девятиклассники Петя, Катя, Ваня, Даша и Наташа бросили жребий,
кому начинать игру. Найдите вероятность того, что начинать игру должен будет
мальчик.
Решение.
Из пятерых детей — мальчиков двое. Поэтому вероятность равна
Ответ: 0,4.
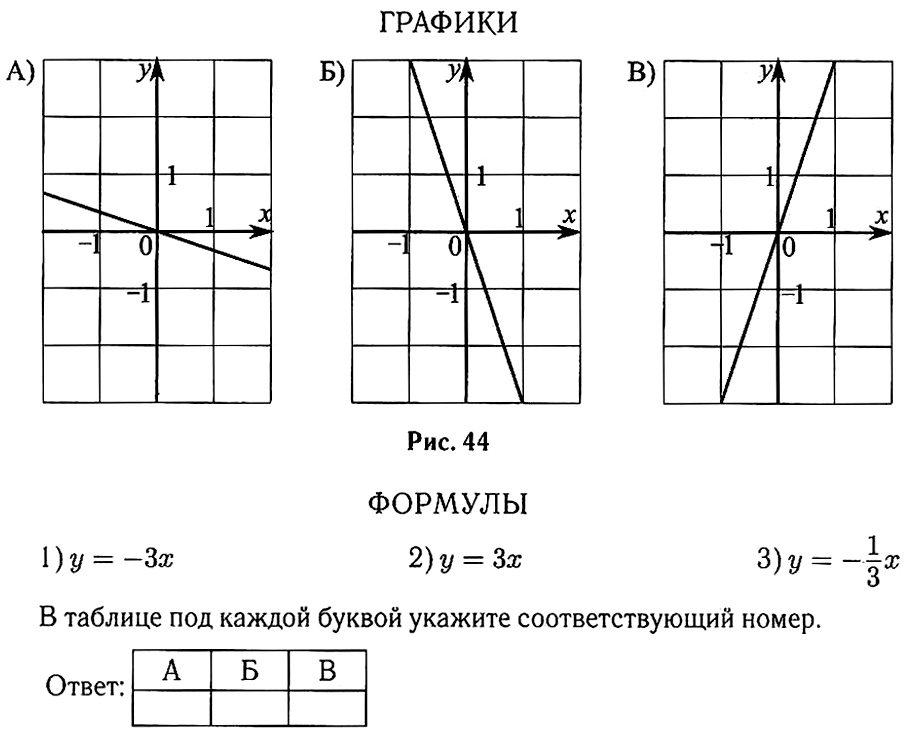
11. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)
Б)
B)
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
Решение.
Определим вид графика каждой из функций:
А) —
уравнение параболы, ветви которой направлены вниз
Б) — уравнение
гиперболы
B) — уравнение
прямой
Найдём для каждого графика функцию: A — 3, Б — 2, В — 1.
Ответ: 321.
12. Радиус описанной около треугольника окружности можно найти по
формуле , где
—
сторона треугольника, — противолежащий этой стороне
угол, а — радиус описанной около этого треугольника окружности. Пользуясь этой
формулой, найдите , если
, а
.
Решение.
Выразим из формулы :
Подставляя, получаем:
Ответ: 0,4.
13. Укажите решение неравенства
1)
2)
3)
4)
Решение.
Последовательно получаем:
Правильный ответ указан под номером: 1.
Ответ: 1
14. При свободном падении тело прошло в первую секунду 5 м, а в каждую
следующую на 10 м больше. Найдите глубину шахты, если свободно падающее тело
достигло его дна через 5 с после начала падения.
Решение.
Составим математическую модель задачи: в первую секунду — 5 м, во
вторую секунду — 15 м, в третью секунду — 25 м, в четвертую секунду — 35 м, в
пятую секунду — 45 м.
Всего
за пять секунд — 5 + 15 + 25 + 35 + 45 = 125 (м).
Ответ: глубина шахты 125 м.
Приведем
другое решение.
Пути, пройденные телом за каждую секунду, представляют собой
арифметическую прогрессию с первым членом a1 = 5 и
разностью d = 10. Путь, пройденный телом за 5 секунд, найдем по
формуле суммы арифметической прогрессии при n = 5:
15.
Найдите острый угол параллелограмма , если биссектриса
угла образует со стороной
угол, равный 41°. Ответ дайте в
градусах.
Решение.

обозначения, как показано на рисунке. Углы и
равны
как накрест лежащие углы при параллельных прямых и
Поскольку
—
биссектриса угла
Сумма смежных углов
параллелограмма равна поэтому угол
равен
Таким образом, острый угол параллелограмма равен
Ответ: 82.
16. 
окружности равна 72, а расстояние от центра окружности до этой хорды равно 27.
Найдите диаметр окружности.
Решение.

построение и введём обозначения, как показано на рисунке. Рассмотрим
треугольники и
они
прямоугольные, — общая,
и
равны
как радиусы окружности, следовательно, эти треугольники равны, откуда По
теореме Пифагора найдём радиус окружности:
Диаметр равен двум радиусам, следовательно,
Ответ: 90.
17. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
Решение.
Диагонали ромба пересекаются под углом 90° и точкой пересечения
делятся пополам. Из прямоугольного треугольника, катетами которого являются
половины диагоналей ромба, а гипотенузой — сторона ромба, по теореме Пифагора
найдем половину неизвестной диагонали: Тогда
вся неизвестная диагональ равна 8.
Площадь ромба равна половине произведения диагоналей:
Ответ: 24.
18.
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный
треугольник. Найдите длину его большего катета.
Решение.
Из рисунка видно, что длина катетов равна 5 и 6. Следовательно,
наибольший катет имеет длину 6.
Ответ: 6
19. Какие из следующих утверждений верны?
1. Через точку, не лежащую на данной прямой, можно провести
прямую, параллельную этой прямой.
2. В тупоугольном треугольнике все углы тупые.
3. Любой квадрат является прямоугольником.
В
ответ запишите номера выбранных утверждений без пробелов, запятых и других
дополнительных символов.
Решение.
Рассмотрим каждое из утверждений:
1. Через точку, не лежащую на данной прямой, можно провести
прямую, параллельную этой прямой — верно.
2. В тупоугольном треугольнике все углы тупые — неверно,
в тупоугольном треугольнике только один из углов тупой.
3. Любой квадрат является прямоугольником — верно,
квадрат есть частный случай прямоугольника.
Ответ: 13
20. Найдите значение выражения если
Решение.
Найдём значение выражения
Поэтому
Ответ: 1.
21. Из городов А и В навстречу друг другу одновременно выехали
мотоциклист и велосипедист. Мотоциклист приехал в В на 42 минуты раньше, чем
велосипедист приехал в А, а встретились они через 28 минут после выезда.
Сколько часов затратил на путь из В в А велосипедист?
Решение.
Пусть — скорость мотоциклиста,
—
скорость велосипедиста. Примем расстояние между городами за единицу.
Мотоциклист и велосипедист встретились через 28 минут, то есть через часа, после выезда,
поэтому Мотоциклист
прибыл в B на 42 минуты раньше, чем велосипедист в А, откуда Получаем
систему уравнений:
Скорость мотоциклиста не может быть отрицательной, поэтому
скорость велосипедиста равна , а
время, затраченное на весь путь равно 1,4 часа.
Ответ: 1,4.
22. Найдите все значения , при которых неравенство
не имеет
решений.
Решение.
График функции — парабола, ветви
которой направлены вверх. Значит, данное неравенство не имеет решений в том и
только том случае, когда эта парабола целиком расположена в верхней полуплоскости.
Отсюда следует, что дискриминант квадратного трёхчлена должен быть
отрицателен.
Найдем четверть дискриминанта: Полученный
квадратный трехчлен отрицателен при
Ответ:
23.
Найдите угол АСО, если его сторона СА касается
окружности, О — центр окружности, а дуга AD окружности,
заключённая внутри этого угла, равна 100°
Решение.
Проведём радиус в точку касания. Так как
—
радиус, а — касательная, то
Угол
— центральный, следовательно, он
равен величине дуги, на которую опирается, Угол
—
развёрнутый, следовательно,
Из треугольника
Ответ: 10°.
24. В параллелограмме ABCD диагонали AC и BD пересекаются
в точке K. Докажите, что площадь параллелограмма ABCD в
четыре раза больше площади треугольника AKB.
Решение.
Проведём высоту так, чтобы она проходила через
точку Углы
и
равны
друг другу как вертикальные. Вспомним также, что диагонали делятся точкой
пересечения пополам, следовательно, Рассмотрим
треугольники и
, они прямоугольные,
имеют равные углы и равные гипотенузы, следовательно, эти треугольники равны, а
значит равны отрезки и
. Таким образом,
Площадь параллелограмм равна а
площадь треугольника
25. На стороне BC остроугольного треугольника ABC (AB≠AC)
как на диаметре построена полуокружность, пересекающая высоту AD в
точке M, AD = 15, MD = 3, H —
точка пересечения высот треугольника ABC. Найдите AH.
Решение.

построения и введём обозначения как указано на рисунке. Угол —
вписанный, опирающийся на диаметр, поэтому он равен 90°. Значит, точка
пересечения прямых и
— точка пересечения
высот Продолжим высоту
до
пересечения с окружностью в точке Получаем, что
По
теореме о секущих получаем, что Треугольники
и
—
прямоугольные, угол — общий, следовательно, эти
треугольники подобны, откуда:
Ответ: 14,4.
6 декабря 2022 13:02
401
компания выбирает место для строительства торгово-развлекательного комплекса:на месте квартал старых одноэтажных домов в центре города или на окраине города.стоимость прокладки 1 метра коммуникации равна 6000 руб.в аренду планирует создавать 4000 кв.м.площади комплекса.стоимость земли цена строительства комплекса с учетом сноса старых зданий и предполагаемая стоимость сдачи в аренду в таблице.обдумав оба варианта компания выбрала место для строительства центр города.Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли,строительство и прокладывания коммуникаций,если компания платит налог 13% стоимости,полученных за сдачу в аренду?Ответ округлите до целых.
Посмотреть ответы
1 млн = 1 000 000
1)
6 000 · 200 = 1 200 000 (руб.) — стоимость прокладки коммуникаций в центре;
1 200 000 руб. = 1,2 млн руб.;
64,4 + 176 + 1,2 = 241,6 (млн руб.) —
затраты на постройку ТРК в центре
.
2)
6 000 · 3 500 = 21 000 000 (руб.) — стоимость прокладки коммуникаций на окраине;
21 000 000 руб. = 21 млн руб.;
11,2 + 168 + 21 = 200,2 (млн руб.) —
затраты на постройку ТРК на окраине
.
3)
241,6 — 200,2 = 41,4 (млн руб.) —
разность в стоимости земли, строительства и прокладывания коммуникаций
.
4)
1 200 — 900 = 300 (руб./месяц) — разность в стоимости аренды за 1 м².
После уплаты налога в 13% аренда принесёт 100%-13%=87% от прибыли без налогов.
1% от чего-то составляет 0,01 долю от того же.
300 · 0,87 = 261 (руб./месяц) — разность в стоимости аренды за 1 м², с учётом уплаты налогов.
261 · 4 000 = 1 044 000 (руб./месяц) —
разность в стоимости аренды за 4 000 м², с учётом уплаты налогов
.
1 044 000 руб./месяц = 1,044 млн руб./месяц
5) (мес.) — время за которое компенсируется разность.
Ответ
: 40.
Еще вопросы по категории Математика
1 млн = 1 000 000
1)
6 000 · 200 = 1 200 000 (руб.) — стоимость прокладки коммуникаций в центре;
1 200 000 руб. = 1,2 млн руб.;
64,4 + 176 + 1,2 = 241,6 (млн руб.) — затраты на постройку ТРК в центре.
2)
6 000 · 3 500 = 21 000 000 (руб.) — стоимость прокладки коммуникаций на окраине;
21 000 000 руб. = 21 млн руб.;
11,2 + 168 + 21 = 200,2 (млн руб.) — затраты на постройку ТРК на окраине.
3)
241,6 — 200,2 = 41,4 (млн руб.) — разность в стоимости земли, строительства и прокладывания коммуникаций.
4)
1 200 — 900 = 300 (руб./месяц) — разность в стоимости аренды за 1 м².
После уплаты налога в 13% аренда принесёт 100%-13%=87% от прибыли без налогов.
1% от чего-то составляет 0,01 долю от того же.
300 · 0,87 = 261 (руб./месяц) — разность в стоимости аренды за 1 м², с учётом уплаты налогов.
261 · 4 000 = 1 044 000 (руб./месяц) — разность в стоимости аренды за 4 000 м², с учётом уплаты налогов.
1 044 000 руб./месяц = 1,044 млн руб./месяц
5)
(мес.) — время за которое компенсируется разность.
Ответ: 40.
Приложения:

Для начала запишем последовательность цифр и определим, какими цифрами зашифрованы магазин, фитнес-центр, мастерская, дом Олега.
Дом Вики обозначен на плане цифрой 4. Магазин отмечен цифрой 7, а фитнес-центр – 5.
Дом Артема зашифрован под цифрой 9. В 30 метрах от детской площадки находится дом Олега под цифрой 1. Ельник обозначен цифрой 6. В угловом доме 8 живет Викин дедушка. Мастерская находится рядом с домом дедушки. Она обозначена цифрой 2. Мебельный центр 10, а рынок обозначен цифрой 3.
Правильная последовательность: 7521.
________________________________________
Детская площадка квадратная со сторонами 5*5 клеток.
Одна клетка равна 15 метров.
Найдем площадь детской площадки: 5*5*15*15= 5625 м2.
Одна плитка имеет параметры 1х1 метр. Площадь плитки равна 1 м2. В одной упаковке 16 плиток.
Получается
5625/16 = 351,5. Округляем в большую сторону. Необходимо приобрести 352 упаковки плитки.
________________________________________________
Здание магазина имеет форму квадрата со сторонами 2х2 клетки.
Площадь магазина равна: 2*2*15*15 = 900 м2.
Фитнес центр прямоугольный. 4х2 клетки.
Площадь фитнес-центра: 4*2*15*15 = 1800 м2.
Суммарная площадь: 900 + 1800 = 2700 м2.
_____________________________________________
Периметр детской площадки: 5*4*15= 300 метров.
_________________________________________________
Стоимость постройки в центре: 58 200 000 + 136 000 000 + 200*5500 = 195 300 000 рублей.
Стоимость постройки гостиницы на окраине города: 11 300 000 + 128 000 000 + 2800*5500 = 154 700 000 рублей.
Разница в стоимости равна 40 600 000 рублей.
Разница в стоимости номера (3200 – 2800)*500 = 200 000 рублей.
Компенсация произойдет через 40 600 000 / 200 000 = 203 дня.
ОГЭ 2020 Математика. Тренировочный вариант № 3 (оффлайн задания) с ответами и решениями. Составлен по проектам демоверсии и спецификации ОГЭ 2020 года (ФИПИ). Посмотреть все варианты тренировочных заданий по математике.
Математика.
Тренировочный вариант 3
Часть 1
Прочитайте внимательно текст и выполните задания 1—5.
На схеме (см. рис.) изображён план застройки участка по адресу: п. Овражки, ул. Солнечная, д. 8. Сторона клетки на плане равна 2 м. Въезд и выезд осуществляются через ворота.
При въезде на участок слева от ворот находится огород (отмеченный цифрой 7), на его территории находится подсобное помещение для сельскохозяйственного инвентаря. Справа от ворот находится сарай для кур и гусей, к которому примыкает выгульный вольер, обозначенный на плане цифрой 5. Рядом с вольером располагается водоём. От ворот до дальнего края участка проходит асфальтовый проезд, заканчивающийся площадкой, также покрытой асфальтом. Рядом с площадкой находится мастерская площадью 32 кв. м и гараж, отмеченный на плане цифрой 3. С другой стороны от площадки расположен жилой дом, окружённый газоном.
1Для объектов, указанных в таблице, определите, какими числами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.
Ответ: ___
2Найдите площадь, которую занимает огород (без учёта площади подсобного помещения для инвентаря). Ответ дайте в квадратных метрах.
Ответ: ___
3Согласно санитарным нормам, в помещении на одном квадратном метре может располагаться до 4 кур или не более 2 гусей. Какое наибольшее число гусей может поместиться в сарае для птиц, если там уже есть 20 кур?
Ответ: ___
4Найдите расстояние от жилого дома до сарая для птиц в метрах. Расстояние измеряйте между двумя ближайшими точками по прямой.
Ответ: ___
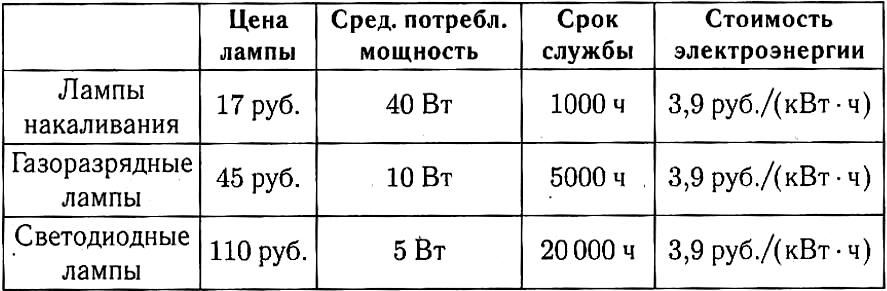
5Хозяин планирует заменить все лампочки накаливания, находящиеся в жилом доме и в хозяйственных постройках, на газоразрядные (их часто называют энергосберегающими) или светодиодные лампы. Характеристики ламп с одинаковым световым потоком и цены на них, а также данные о стоимости электроэнергии даны в таблице.
Сколько рублей экономии при потреблении электроэнергии и сокращении числа заменяемых ламп получит хозяин за 1 год (365 дней), если 20 лампочек накаливания в жилом доме и 10 лампочек накаливания в других помещениях он заменит на светодиодные лампы? Считайте, что в сутки каждая лампа горит 10 ч и лампы накаливания пришлось бы заменять за год 3 раза.
Ответ: ___
6 Найдите значение выражения
Ответ: ___
7О числах k, l, m, n известно, что k < m, l > k, n = m. Сравните m и l.
1) l = m 2) l > m 3) l < m 4) сравнить невозможно
Ответ: ___
8Найдите значение выражения (1,8 • 10–1) • (4 • 10–2).
Ответ: ___
9Решите уравнение 6х2 – 4х – 5 = х2 – 3х – 1. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Ответ: ___
10В каждой сороковой пачке печенья согласно условиям акции есть приз. Призы распределены по пачкам случайно. Андрей покупает пачку печенья в надежде выиграть приз. Найдите вероятность того, что Андрей не найдёт приз в своей пачке.
Ответ: ___
11Установите соответствие между графиками функций (см. рис. 44) и формулами, которые их задают.
12Дана арифметическая прогрессия (аn), разность которой равна –2,3, a1 = –7,1. Найдите а10.
Ответ: ___
13Найдите значение выражения
Ответ: ___
14Мощность постоянного тока (в ваттах) вычисляется по формуле Р = I2R, где I – сила тока (в амперах), R – сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 415 Вт, а сила тока равна 2,5 А.
Ответ: ___
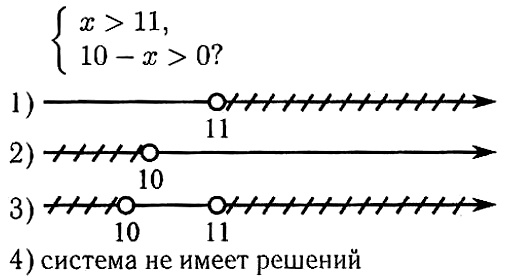
15На каком рисунке изображено множество решений системы неравенств
Ответ: ___
16Найдите площадь прямоугольного треугольника, если катет и гипотенуза равны соответственно 12 и 15.
Ответ: ___
17Найдите площадь квадрата, если его диагональ равна 2 (см. рис. 45).
Ответ: ___
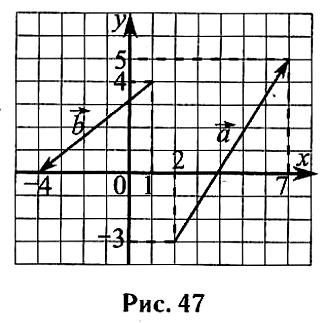
18На окружности с центром О отмечены точки А и В так, что ∠AOB = 82° (см. рис. 46). Длина меньшей дуги АВ равна 41. Найдите длину большей дуги.
Ответ: ___
19На рисунке 47 изображены векторы а и b. Найдите их скалярное произведение.
Ответ: ___
20Какие из следующих утверждений верны?
- Диагонали любого квадрата делят его на 4 равных треугольника.
- Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
- Средняя линия трапеции равна сумме её оснований.
В ответе запишите номера выбранных утверждений без пробелов, занятых и других дополнительных символов.
Ответ: ___
Смотреть ОТВЕТЫ на задания 1-20

Часть 2
21Решите уравнение 4х3 + bх2 = 4х + 5.
Смотреть решение и ответ
22Константин, Николай, Олег и Марина учредили компанию с уставным капиталом 800000 рублей. Константин внёс 23% уставного капитала, Марина – 248000 рублей, Олег – 9/10 уставного капитала, а оставшуюся часть капитала внёс Николай. Учредители договорились делить ежегодную прибыль пропорционально внесённому в уставной капитал вкладу. Какая сумма от прибыли 1200000 рублей причитается Николаю? Ответ дайте в рублях.
Смотреть решение и ответ
23Постройте график функции у = х2 – 2|х| – 3. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Смотреть решение и ответ
24В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 8.
Смотреть решение и ответ
25Окружности с центрами Q1 и Q2 пересекаются в точках М и N, причём точки Q1 и Q2 лежат по одну сторону от прямой MN. Докажите, что Q1Q2 ⊥ MN.
Смотреть решение и ответ
26В треугольнике РМК известно, что РМ = 12, РК = 18, точка О – центр окружности, описанной около треугольника РМК. Прямая MS, перпендикулярная прямой РО, пересекает сторону РК в точке S. Найдите SK.
Смотреть решение и ответ
ОГЭ 2020 Математика. Тренировочный вариант № 3 (оффлайн задания) с ответами и решениями. Составлен по проектам демоверсии и спецификации ОГЭ 2020 года (ФИПИ).
Посмотреть все варианты тренировочных заданий по математике.
Детскую площадку решили покрыть резиновой плиткой размером 1 м × 1 м каждая. Плитка продаётся упаковками по 16 штук. Какое минимальное количество упаковок плитки необходимо приобрести?
На плане (см. рисунок) изображён район города, в котором проживает Вика. Сторона каждой клетки на плане равна 15 м. Рядом с домом Вики, обозначенным на плане цифрой 4, находится одноэтажный магазин площадью 900 м2 и фитнес‐центр. В 15 м от магазина расположен дом, где живёт одноклассник Вики Артём. В 30 м от детской площадки находится дом, где живёт Олег. Если выйти из фитнес‐центра, пройти небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по ремонту бытовой техники. Через дорогу от дома дедушки расположен рынок, а недалеко от него – мебельный центр площадью 2025 м2.
1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Магазин | Фитнес‐центр | Мастерская | Дом, где живёт Олег |
|---|---|---|---|---|
| Цифры |
Источник: Тренировочный вариант № 232, усложнённый, Александр Ларин
2
Найдите суммарную площадь, которую занимают магазин и фитнес-центр. Ответ дайте в м2.
Источник: Тренировочный вариант № 232, усложнённый, Александр Ларин
3
По периметру детской площадки планируется поставить забор. Найдите его длину (в метрах).
Источник: Тренировочный вариант № 232, усложнённый, Александр Ларин
4
Фирма выбирает место для строительства гостиницы: в центре города или на его окраине. Стоимость прокладки 1 метра коммуникаций равна 5500 рублей. В гостинице планируется сдавать 500 номеров. Стоимость земли, цена строительства гостиницы и средняя стоимость номера даны в таблице.
| Место | Цена земли (млн руб.) |
Цена строительства (млн руб.) |
Длина коммуникаций (м) |
Стоимость номера (руб./сутки) |
|---|---|---|---|---|
| Центр | 58,2 | 136 | 200 | 3200 |
| Окраина | 11,3 | 128 | 2800 | 2800 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько суток после начала сдачи номеров (при условии полной загрузки гостиницы) более высокая стоимость номеров компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций?
Источник: Тренировочный вариант № 232, усложнённый, Александр Ларин
Решение.
Найдём площадь детской площадки:
м2.
Одна плитка имеет площадь 1 м2. Значит, потребуется упаковок плитки. Таким образом, необходимо приобрести 352 упаковки плитки.
Ответ: 352.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Магазин | Фитнес‐центр | Мастерская | Дом, где живёт Олег |
|---|---|---|---|---|
| Цифры |
Показать
Ответ:
2
Детскую площадку решили покрыть резиновой плиткой размером 1 м × 1 м каждая. Плитка продаётся упаковками по 16 штук. Какое минимальное количество упаковок плитки необходимо приобрести?
Показать
Ответ:
3
Найдите суммарную площадь, которую занимают магазин и фитнес-центр. Ответ дайте в м2.
Показать
Ответ:
4
По периметру детской площадки планируется поставить забор. Найдите его длину (в метрах).
Показать
Ответ:
5
Фирма выбирает место для строительства гостиницы: в центре города или на его окраине. Стоимость прокладки 1 метра коммуникаций равна 5500 рублей. В гостинице планируется сдавать 500 номеров. Стоимость земли, цена строительства гостиницы и средняя стоимость номера даны в таблице.
| Место | Цена земли (млн руб.) |
Цена строительства (млн руб.) |
Длина коммуникаций (м) |
Стоимость номера (руб./сутки) |
|---|---|---|---|---|
| Центр | 58,2 | 136 | 200 | 3200 |
| Окраина | 11,3 | 128 | 2800 | 2800 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько суток после начала сдачи номеров (при условии полной загрузки гостиницы) более высокая стоимость номеров компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций?
Показать
Ответ:
6
Укажите наибольшее из следующих чисел:
Ответ:
7
На координатной прямой отмечено число a.
Найдите наименьшее из чисел a2, a3, a4.
В ответе укажите номер правильного варианта.
1) a2
2) a3
3) a4
4) не хватает данных для ответа
Ответ:
8
Упростите выражение и найдите его значение при
. В ответе запишите полученное число.
Ответ:
9
Решите уравнение .
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Ответ:
10
Фирма «Вспышка» изготавливает фонарики. Вероятность того, что случайно выбранный фонарик из партии бракованный, равна 0,02. Какова вероятность того, что два случайно выбранных из одной партии фонарика окажутся небракованными?
Ответ:
11
Найдите значение k по графику функции изображенному на рисунке.
Ответ:
12
13
Укажите решение неравенства
| 1)
|
2)
|
| 3)
|
4)
|
Ответ:
14
Васе надо решить 434 задачи. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Вася решил 5 задач. Определите, сколько задач решил Вася в последний день, если со всеми задачами он справился за 14 дней.
Ответ:
15
Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Ответ:
16
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.
Ответ:
17
Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции.
Ответ:
18
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AC.
Ответ:
19
Какое из следующих утверждений верно?
1) Диагонали параллелограмма равны.
2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Если утверждений несколько, запишите их номера в порядке возрастания.
Ответ:
20
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
21
Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
22
Найдите все значения a, при которых неравенство не имеет решений.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
23
Медианы треугольника ABC пересекаются в точке M. Найдите длину медианы, проведённой к стороне BC, если угол BAC равен 47°, угол BMC равен 133°, .
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
24
Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
25
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
ПОДЕЛИТЬСЯ
Новый сентябрьский тренировочный вариант (тренировочная работа) №37446019 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.
Ссылка для скачивания варианта: задания (КИМ)
Ответы и решения для варианта: скачать
Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37446019
Ответы и решения для заданий ОГЭ 2022
На плане (см. рисунок) изображён район города, в котором проживает Вика. Сторона каждой клетки на плане равна 15 м. Рядом с домом Вики, обозначенным на плане цифрой 4, находится одноэтажный магазин площадью 900 м 2 и фитнес‐ центр. В 15 м от магазина расположен дом, где живёт одноклассник Вики Артём. В 30 м от детской площадки находится дом, где живёт Олег. Если выйти из фитнес‐центра, пройти небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по ремонту бытовой техники. Через дорогу от дома дедушки расположен рынок, а недалеко от него – мебельный центр площадью 2025 м 2 .
Задание 1 №368420 Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Правильный ответ: 7521
Задание 2 №368421 Детскую площадку решили покрыть резиновой плиткой размером 1 м × 1 м каждая. Плитка продаётся упаковками по 16 штук. Какое минимальное количество упаковок плитки необходимо приобрести?
Правильный ответ: 352
Задание 3 №368422 Найдите суммарную площадь, которую занимают магазин и фитнес-центр. Ответ дайте в м 2 .
Правильный ответ: 2700
Задание 4 №368424 По периметру детской площадки планируется поставить забор. Найдите его длину (в метрах).
Правильный ответ: 300
Задание 5 №368425 Фирма выбирает место для строительства гостиницы: в центре города или на его окраине. Стоимость прокладки 1 метра коммуникаций равна 5500 рублей. В гостинице планируется сдавать 500 номеров. Стоимость земли, цена строительства гостиницы и средняя стоимость номера даны в таблице. Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько суток после начала сдачи номеров (при условии полной загрузки гостиницы) более высокая стоимость номеров компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций?
Правильный ответ: 203
Задание 10 №316354 Фирма «Вспышка» изготавливает фонарики. Вероятность того, что случайно выбранный фонарик из партии бракованный, равна 0,02. Какова вероятность того, что два случайно выбранных из одной партии фонарика окажутся небракованными?
Правильный ответ: 0,9604
Задание 14 №393946 Васе надо решить 434 задачи. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Вася решил 5 задач. Определите, сколько задач решил Вася в последний день, если со всеми задачами он справился за 14 дней.
Правильный ответ: 57
Задание 15 №323537 Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Правильный ответ: 78
Задание 16 №348379 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.
Правильный ответ: 60
Задание 17 №311480 Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции.
Правильный ответ: 17
Задание 18 №341709 На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AC.
Правильный ответ: 4
Задание 19 №341332 Какое из следующих утверждений верно? 1) Диагонали параллелограмма равны. 2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне. 3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Правильный ответ: 2
Задание 21 №338603 Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Правильный ответ: 75
Задание 24 №333131 Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
Задание 25 №315126 Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
Правильный ответ: 14
Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:
-
Тренировочный вариант №18 ОГЭ 2022 по математике 9 класс с ответами
-
Тренировочный вариант Ларина №290 ОГЭ 2022 по математике 9 класс
Огэ по математике 367694
ОГЭ Задние «Компания выбирает место для строительства.» , как выполнить?
Компания выбирает место для строительства торгово‐развлекатель ного комплекса: на месте квартала старых одноэтажных домов в центре города или на окраине города. Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется сдавать 4000 м2 площади комплекса. Стоимость земли, цена строительства комплекса с учётом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций? Ответ округлите до целых.
Дано: 4000 м² площади под сдачу. В центре 200 метров коммуникаций по 6 000 руб. Итог 200 х 6 000 = 1 200 000 руб = 1.2 млн руб. Но кроме этого нужно заплатить за землю и строительство на ней. В итоге выйдет:
64.4 + 176 + 1.2 = 246.6 млн. руб.
Если сдавать в аренду, то потребуется сколько месяцев, чтобы выйти в нуль и начать получать прибыль? Считаем:
4000 х 1200 = 4 800 000 руб = 4.8 млн. руб.
246.6/4.8 = 51.375 месяцев = 4 года и 3.375 месяца ~ 4 г.4м. Странное предприятие, не рентабельное, но это же арифметическая задача без учёта инфляции.
А чтобы было если они строили на окраине? Считаем:
На окраине 3500 метров коммуникаций по 6 000 руб. Итог 3500 х 6 000 = 21 000 000 руб = 21 млн руб. Но кроме этого нужно заплатить за землю и строительство на ней. В итоге выйдет:
11.2 + 168 + 21 = 202.2 млн. руб.
А сколько они бы получили с аренды? 4000 х 900 = 3 600 000 руб. = 3.6 млн. руб.
Если сдавать в аренду, то потребуется сколько месяцев, чтобы выйти в нуль и начать получать прибыль? Считаем:
202.2/3.6 = 56.166 месяцев = 4 года и 8.166 месяцев. Чуть меньше пятилетки выброс денег на ветер.
Но какова разница? В центре, чтобы начать получать доход потребуется 51.375; на окраине 56.166 месяцев.
Компания выбирает место для строительства торгово развлекатель ного комплекса на месте квартала старых одноэтажных домов в центре города или на окраине города.
Www. bolshoyvopros. ru
30.12.2017 19:29:29
2017-12-30 19:29:29
Источники:
Http://www. bolshoyvopros. ru/questions/3546228-oge-zadnie-kompanija-vybiraet-mesto-dlja-stroitelstva-kak-vypolnit. html
Компания выбирает место для строительства торгово-развлекательного комплекса: на месте квартал — Школьные » /> » /> .keyword { color: red; } Огэ по математике 367694
Компания выбирает место для строительства торгово-развлекательного комплекса: на месте квартал старых одноэтажных домов в центре города или на окраине ость прокладки 1 метра коммуникации равна 6000 руб. в аренду планирует создавать 4000 ди ость земли цена строительства комплекса с учетом сноса старых зданий и предполагаемая стоимость сдачи в аренду в ав оба варианта компания выбрала место для строительства центр сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительство и прокладывания коммуникаций, если компания платит налог 13% стоимости, полученных за сдачу в аренду? Ответ округлите до целых.
Компания выбирает место для строительства торгово-развлекательного комплекса:на месте квартал старых одноэтажных домов в центре города или на окраине города. стоимость прокладки 1 метра коммуникации равна 6000 руб. в аренду планирует создавать 4000 кв. м.площади комплекса. стоимость земли цена строительства комплекса с учетом сноса старых зданий и предполагаемая стоимость сдачи в аренду в таблице. обдумав оба варианта компания выбрала место для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительство и прокладывания коммуникаций, если компания платит налог 13% стоимости, полученных за сдачу в аренду? Ответ округлите до целых.
64,4 + 176 + 1,2 = 241,6 (млн руб.) — Затраты на постройку ТРК в центре.
6 000 · 3 500 = 21 000 000 (руб.) — стоимость прокладки коммуникаций на окраине;
21 000 000 руб. = 21 млн руб.;
11,2 + 168 + 21 = 200,2 (млн руб.) — Затраты на постройку ТРК на окраине.
241,6 — 200,2 = 41,4 (млн руб.) — Разность в стоимости земли, строительства и прокладывания коммуникаций.
1 200 — 900 = 300 (руб./месяц) — разность в стоимости аренды за 1 м².
После уплаты налога в 13% аренда принесёт 100%-13%=87% от прибыли без налогов.
1% от чего-то составляет 0,01 долю от того же.
300 · 0,87 = 261 (руб./месяц) — разность в стоимости аренды за 1 м², с учётом уплаты налогов.
261 · 4 000 = 1 044 000 (руб./месяц) — Разность в стоимости аренды за 4 000 м², с учётом уплаты налогов.
261 4 000 1 044 000 руб.
Znanija. com
15.12.2020 2:55:22
2020-12-15 02:55:22
Источники:
Https://znanija. com/task/33392957
OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Огэ по математике 367694
Огэ по математике 367694
Огэ по математике 367694
Задание 5 № 367694
Компания выбирает место для строительства торгово‐развлекательного комплекса: на месте квартала старых одноэтажных домов в центре города или на окраине города. Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется сдавать 4000 м 2 площади комплекса. Стоимость земли, цена строительства комплекса с учётом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.
МестоЦена земли
| Центр | 64,4 | 176 | 200 | 1200 |
| Окраина | 11,2 | 168 | 3500 | 900 |
(млн руб.)Цена
Строительства
(млн руб.)Длина
Коммуникаций
(м)Стоимость
Аренды за 1 м 2
(руб./месяц)
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций? Ответ округлите до целых.
На плане (см. рисунок) изображён район города, в котором живёт Петя. Сторона каждой клетки на плане равна 10 м.
Дом, в котором живёт Петя, обозначен цифрой 6. Прямо напротив дома, где живёт Петя, через дорогу находится дом в форме буквы «Г», где живёт его друг Вася. Рядом с домом, где живёт Петя, расположен дом, где живёт одноклассница Таня, а напротив него через дорогу имеется здание банка площадью 600 м 2 . А с другой стороны дома, где живёт Таня, расположен детский сад. Недалеко от детского сада и дома, где живёт Петя, находится магазин. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах от неё — квартал старых одноэтажных домов.
Задание 1 № 367690
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Объекты
| Банк | Магазин | Дом, где живёт Таня |
Квартал старых Домов |
Цифры
Рядом с домом, где живёт Петя, расположен дом, где живёт одноклассница Таня, а напротив него через дорогу имеется здание банка площадью 600 м 2 . Значит, Банк отмечен цифрой 3, а дом, где живёт Таня, отмечен цифрой 2. Недалеко от детского сада и дома, где живёт Петя, находится магазин, следовательно, магазин отмечен цифрой 5. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах от неё — квартал старых одноэтажных домов, значит, квартал старых домой обозначен цифрой 8.
Задание 5 № 367694
Задание 1 № 367690
Месяц Центр 64,4 176 200 1200 Окраина 11,2 168 3500 900.
Oge. sdamgia. ru
12.03.2019 23:24:02
2019-03-12 23:24:02
Источники:
Https://oge. sdamgia. ru/problem? id=367694
Тип 1 № 367690
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Банк | Магазин | Дом, где живёт Таня | Квартал старых домов |
|---|---|---|---|---|
| Цифры |
На плане (см. рис.) изображён район города, в котором живёт Петя. Сторона каждой клетки на плане равна 10 м.
Дом, в котором живёт Петя, обозначен цифрой 6. Прямо напротив дома, где живёт Петя, через дорогу находится дом в форме буквы «Г», где живёт его друг Вася. Рядом с домом, где живёт Петя, расположен дом, где живёт одноклассница Таня, а напротив него через дорогу имеется здание банка площадью 600 м2. А с другой стороны дома, где живёт Таня, расположен детский сад. Недалеко от детского сада и дома, где живёт Петя, находится магазин. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах от неё — квартал старых одноэтажных домов.
2. Тип 2 № 367691
Территорию стадиона необходимо засеять газонной травой. В одной упаковке газонной травы содержится 12 кг семян, при этом для засеивания 3 м2 земли необходимо 100 г семян. Какое минимальное количество упаковок газонной травы необходимо приобрести?
3. Тип 3 № 367692
Найдите суммарную площадь, которую занимают дома, где проживают Таня, Петя и Вася. Ответ дайте в м2.
4. Тип 4 № 367693
Найдите расстояние от дома, где живёт Петя, до автобусной остановки (расстояние между двумя ближайшими точками по прямой) в метрах.
5. Тип 5 № 367694
Компания выбирает место для строительства торгово‐развлекательного комплекса: на месте квартала старых одноэтажных домов в центре города или на окраине города. Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется сдавать 4000 м2 площади комплекса. Стоимость земли, цена строительства комплекса с учётом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.
| Место | Цена земли (млн руб.) | Цена строительства (млн руб.) | Длина коммуникаций (м) | Стоимость аренды за 1 м2 (руб./месяц) |
|---|---|---|---|---|
| Центр | 64,4 | 176 | 200 | 1200 |
| Окраина | 11,2 | 168 | 3500 | 900 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций? Ответ округлите до целых.
6. Тип 6 № 337273
Найдите значение выражения
7. Тип 7 № 341320
На координатной прямой точками отмечены числа
Какому числу соответствует точка B?
1)
2)
3) 0,42
4) 0,45
8. Тип 8 № 338092
Найдите если
9. Тип 9 № 338503
Решите уравнение
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. Тип 10 № 311391
Какова вероятность того, что случайно выбранное натуральное число от 15 до 29 делится на 5?
11. Тип 11 № 351965
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)
Б)
В)
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
12. Тип 12 № 311528
Площадь треугольника можно вычислить по формуле
, где a — сторона треугольника, h — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону
, если площадь треугольника равна
, а высота h равна 14 м.
13. Тип 13 № 320666
Укажите неравенство, решением которого является любое число.
В ответе укажите номер правильного варианта.
1) x2 − 15 < 0
2) x2 + 15 > 0
3) x2 + 15 < 0
4) x2 − 15 > 0
14. Тип 14 № 394399
Мать дарит каждой из пяти своих дочерей в день рождения, начиная с пяти лет, столько книг, сколько дочери лет. Возрасты пяти дочерей составляют арифметическую прогрессию, разность которой равна 2. Сколько лет было старшей дочери, когда у них составилась библиотека общей численностью в 495 книг?
15. Тип 15 № 311412
Углы, отмеченные на рисунке одной дугой, равны. Найдите угол α. Ответ дайте в градусах.
16. Тип 16 № 102
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
17. Тип 17 № 39
Найдите площадь трапеции, изображённой на рисунке.
18. Тип 18 № 348467
На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник. Найдите длину его большего катета.
19. Тип 19 № 341525
Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Сумма углов любого треугольника равна 360 градусам.
3) Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Тип 20 № 311599
Какое из чисел больше: или
?
21. Тип 21 № 314431
При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?
22. Тип 22 № 338207
Постройте график функции и определите, при каких значениях m прямая
имеет с графиком ровно две общие точки.
23. Тип 23 № 311666
Диагонали AC и BD трапеции ABCD пересекаются в точке O. Площади треугольников AOD и BOC равны соответственно и
. Найдите площадь трапеции.
24. Тип 24 № 311969
Окружность касается стороны AB треугольника ABC, у которого ∠C = 90°, и продолжений его сторон AC и BC за точки A и B соответственно. Докажите, что периметр треугольника ABC равен диаметру этой окружности.
25. Тип 25 № 333027
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 16 и 48, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.

















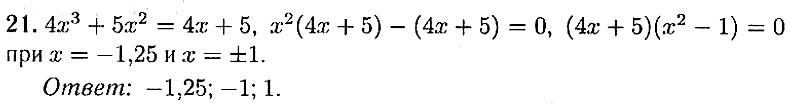









.jpg)
