Время на прочтение
8 мин
Количество просмотров 11K
Сортировку кучей (она же — пирамидальная сортировка) на Хабре уже поминали добрым словом не раз и не два, но это всегда была достаточно общеизвестная информация. Обычную бинарную кучу знают все, но ведь в теории алгоритмов также есть:
n-нарная куча; куча куч, основанная на числах Леонардо; дерамида (гибрид кучи и двоичного дерева поиска); турнирная мини-куча; зеркальная (обратная) куча; слабая куча; юнгова куча; биномиальная куча; и бог весть ещё какие кучи…
И умнейшие представители computer science в разные годы предложили свои алгоритмы сортировки с помощью этих пирамидальных структур. Кому интересно, что у них получилось — для тех начинаем небольшую серию статей, посвящённую вопросам сортировки с помощью этих структур. Мир куч многообразен — надеюсь, вам будет интересно.
Статья написана при поддержке компании EDISON.Мы занимаемся разработкой мобильных приложений и предоставляем услуги по тестированию программного обеспечения.
Мы очень любим теорию алгоритмов!

Есть такой класс алгоритмов — сортировки выбором. Общая идея — неупорядоченная часть массива уменьшается за счёт того, что в ней ищутся максимальные элементы, которые из неё переставляются в увеличивающуюся отсортированную область.
Сортировка обычным выбором — это брутфорс. Если в поисках максимумов просто линейно проходить по массиву, то временнáя сложность такого алгоритма не может превысить O(n2).
Куча
Наиболее эффективный способ работать с максимумами в массиве — это организовать данные в специальную древовидную структуру, известную как куча. Это дерево, в котором все родительские узлы не меньше чем узлы-потомки.
Другие названия кучи — пирамида, сортирующее дерево.
Давайте разберём, как это можно легко и почти бесплатно представить массив в виде дерева.
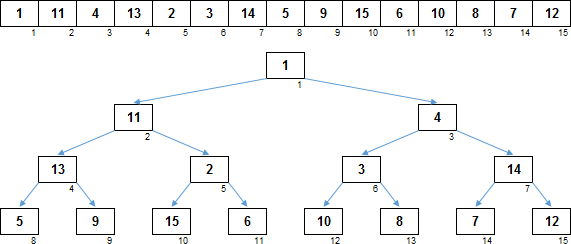
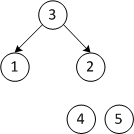
Возьмём самый первый элемент массива и будем считатть, что это корень дерева — узел 1-го уровня. Следующие 2 элемента — это узлы 2-го уровня, правый и левый потомки корневого элемента. Следующие 4 элемента — это узлы 3-го уровня, правые/левые потомки второго/третьего элемента массива. Следующие 8 элементов — узлы 4-го уровня, потомки элементов 3-го уровня. И т.д. На этом изображении узлы бинарного дерева наглядно расположены строго под соответствующими элементами в массиве:
Хотя, деревья на диаграммах чаще изображают в такой развёртке:
Если смотреть под таким углом, то тогда понятно почему сортировку кучей называют пирамидальной сортировкой. Хотя, это примерно тоже самое, как если шахматного слона называть офицером, ладью — турой, а ферзя — королевой.
Индексы потомков для i-го элемента определяются элементарно (если индекс самого первого элемента массива считать равным 0, как принято в подавляющем большинстве языков программирования):
Левый потомок: 2 × i + 1
Правый потомок: 2 × i + 2
(У меня на диаграммах и анимациях традиционно индексы массивов начинаются с 1, там формулы слегка отличаются: левый потомок:
2 × i
и правый потомок:
2 × i + 1
, но это уже мелкие арифметические нюансы).
Если получающиеся по этим формулам индексы потомков выходят за пределы массива, значит у i-го элемента потомков нет. Также может статься что у i-го элемента есть левый потомок (приходится на самый последний элемент массива, в котором нечётное количество элементов), но уже нет правого.
Итак, любой массив можно легко представить в виде дерева, однако это пока ещё не куча, потому что, в массиве некоторые элементы-потомки могут оказаться больше чем их элементы-родители.
Чтобы наше дерево, созданное на основе массива, стало кучей, его нужно как следует просеять.
Просейка
Душой сортировки кучей является просейка.
Просеивание для элемента состоит в том, что если он меньше по размеру чем потомки, объединённых в неразрывную цепочку, то этот элемент нужно переместить как можно ниже, а бо́льших потомков по ветке поднять наверх на 1 уровень.
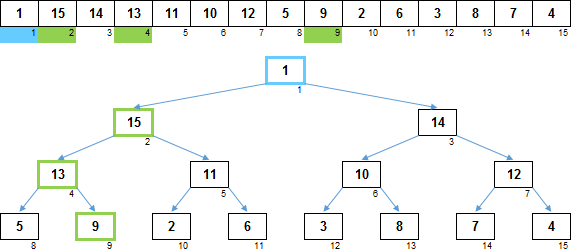
На изображении показан путь просейки для элемента. Синим цветом обозначен элемент для которого осуществляется просейка. Зелёный цвет — бо́льшие потомки вниз по ветке. Они будут подняты на один уровень вверх, поскольку по величине превосходят синий узел, для которого делается просейка. Сам элемент из самого верхнего синего узла будет перемещён на место самого нижнего потомка из зелёной цепочки.
Просейка нужна для того, чтобы из обычного дерева сделать сортирующее дерево и в дальнейшем поддерживать дерево в таком (сортирующем) состоянии.
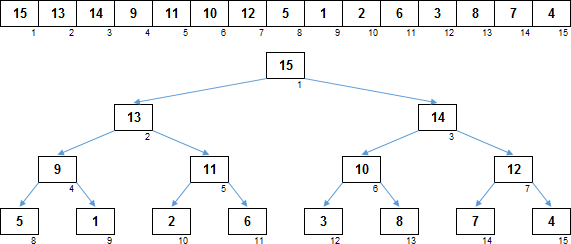
На этом изображении элементы массива перераспределены так, что он уже разложен именно в кучу. Хотя массив раскладывается в сортирующее дерево, сам он пока что не отсортирован (ни по возрастанию ни по убыванию), хотя все потомки в дереве меньше чем их родительские узлы. Но зато самый максимальный элемент в сортирующем дереве всегда находится в главном корне, что очень важно.
Сортировка кучей :: Heapsort
Алгоритм на самом деле простой:
- Этап 1. Формируем из всего массива сортирующее дерево. Для этого проходим справа-налево элементы (от последних к первым) и если у элемента есть потомки, то для него делаем просейку.
- Этап 2. Максимумы ставим в конец неотсортированной части массива. Так как данные в массиве после первого этапа представляют из себя сортирующее дерево, максимальный элемент находится на первом месте в массиве. Первый элемент (он же максимум) меняем с последним элементом неотсортированной части массива местами. После этого обмена максимум оказался своём окончательном месте, т.е. максимальный элемент отсортирован. Неотсортированная часть массива перестала быть сортирующим деревом, но это исправляется однократной просейкой — в результате чего на первом месте массива оказывается предыдущий по величине максимальный элемент. Действия этого этапа снова повторяются для оставшейся неупорядоченной области, до тех пор пока максимумы поочерёдно не будут перемещены на свои окончательные позиции.
Код на Питоне классической реализации пирамидальной сортировки:
# Основной алгоритм сортировки кучей
def HeapSort(data):
# Формируем первоначальное сортирующее дерево
# Для этого справа-налево перебираем элементы массива
# (у которых есть потомки) и делаем для каждого из них просейку
for start in range((len(data) - 2) / 2, -1, -1):
HeapSift(data, start, len(data) - 1)
# Первый элемент массива всегда соответствует корню сортирующего дерева
# и поэтому является максимумом для неотсортированной части массива.
for end in range(len(data) - 1, 0, -1):
# Меняем этот максимум местами с последним
# элементом неотсортированной части массива
data[end], data[0] = data[0], data[end]
# После обмена в корне сортирующего дерева немаксимальный элемент
# Восстанавливаем сортирующее дерево
# Просейка для неотсортированной части массива
HeapSift(data, 0, end - 1)
return data
# Просейка свеху вниз, в результате которой восстанавливается сортирующее дерево
def HeapSift(data, start, end):
# Начало подмассива - узел, с которого начинаем просейку вниз
root = start
# Цикл просейки продолжается до тех пор,
# Пока встречаются потомки, большие чем их родитель
while True:
child = root * 2 + 1 # Левый потомок
# Левый потомок за пределами подмассива - завершаем просейку
if child > end: break
# Если правый потомок тоже в пределах подмассива,
# то среди обоих потомков выбираем наибольший
if child + 1 <= end and data[child] < data[child + 1]:
child += 1
# Если больший потомок больше корня, то меняем местами
# при этом больший потомок сам становится корнем,
# от которого дальше опускаемся вниз по дереву
if data[root] < data[child]:
data[root], data[child] = data[child], data[root]
root = child
else:
breakСложность алгоритма
Чем хороша простая куча — её не нужно отдельно хранить, в отличие от других видов деревьев (например, двоичное дерево поиска на основе массива прежде чем использовать нужно сначала создать). Любой массив уже является деревом, в котором прямо на ходу можно сразу определять родителей и потомков. Сложность по дополнительной памяти O(1), всё происходит сразу на месте.
Что касается сложности по времени, то она зависит от просейки. Однократная просейка обходится в
O(log n)
. Сначала мы для n элементов делаем просейку, чтобы из массива построить первоначальную кучу — этот этап занимает
O(n log n)
. На втором этапе мы при вынесении n текущих максимумов из кучи делаем однократную просейку для оставшейся неотсортированной части, т.е. этот этап также стоит нам
O(n log n)
.
Итоговая сложность по времени: O(n log n) + O(n log n) = O(n log n).
При этом у пирамидальной сортировки нет ни вырожденных ни лучших случаев. Любой массив будет обработан на приличной скорости, но при этом не будет ни деградации ни рекордов.
Сортировка кучей в среднем работает несколько медленнее чем быстрая сортировка. Но для quicksort можно подобрать массив-убийцу, на котором компьютер зависнет, а вот для heapsort — нет.
Сортировка тернарной кучей :: Ternary heapsort
Давайте рассмотрим троичную кучу. От двоичной она, вы не поверите, отличается только тем, что у родительских узлов максимум не два, а три потомка. В тернарной куче для i-го элемента индексы его трёх потомков вычисляются аналогично (если у первого элемента индекс = 0):
Левый потомок: 3 × i + 1
Средний потомок: 3 × i + 2
Правый потомок: 3 × i + 3
(Если индексы начинать с 1, как на анимациях в этой статье, то в этих формулах надо просто отнять единицу).
Процесс сортировки:
С одной стороны заметно уменьшается количество уровней в дереве по сравнению с двоичной кучей, что означает, что в среднем при просейке будет происходить меньше свопов. С другой стороны, для нахождения минимального потомка понадобится больше сравнений — ведь потомков теперь не по два, а по три. В общем, в плане сложности по времени — где-то находим, где-то теряем, однако в целом тоже самое. Данные в тернарной куче сортируется немного быстрее чем в бинарной, но это убыстрение весьма незначительное. Во всех вариациях пирамидальной сортировки разработчики алгоритмов предпочитают брать именно двоичный вариант, потому что троичный якобы сложнее в реализации (хотя это «сложнее» заключается в добавлении в алгоритм буквально пары-тройки дополнительных строк), а выигрыш по скорости минимален.
Сортировка n-нарной кучей :: N-narny heapsort
Разумеется, можно не останавливаться на достигнутом и адаптировать сортировку кучей для любого числа потомков. Может быть, если и дальше увеличивать количества потомков, можно существенно повысить скорость процесса?
Для i-го элемента массива индексы (если отсчитывать их с нуля) его N потомков вычисляются очень просто:
1-й потомок: N × i + 1
2-й потомок: N × i + 2
3-й потомок: N × i + 3
…
N-й потомок: N × i + N
Код на Python сортировки N-нарной кучей:
# Основной алгоритм сортировки кучей для N потомков
def NHeapSort(data):
n = 3 # Сколько потомков у родителя
# Формируем первоначальное сортирующее дерево
# Для этого справа-налево перебираем элементы массива
# (у которых есть потомки) и делаем для каждого из них просейку
for start in range(len(data), -1, -1):
NHeapSift(data, n, start, len(data) - 1)
# Первый элемент массива всегда соответствует корню сортирующего дерева
# и поэтому является максимумом для неотсортированной части массива.
for end in range(len(data) - 1, 0, -1):
# Меняем этот максимум местами с последним
# элементом неотсортированной части массива
data[end], data[0] = data[0], data[end]
# После обмена в корне сортирующего дерева немаксимальный элемент
# Восстанавливаем сортирующее дерево
# Просейка для неотсортированной части массива
NHeapSift(data, n, 0, end - 1)
return data
# Просейка сверху-вниз для родителя у которого N потомков
def NHeapSift(data, n, start, end):
# Начало подмассива - узел, с которого начинаем просейку вниз
root = start
while True:
# Первого потомка (если он в пределах подмассива)
# назначаем максимальным потомком
child = root * n + 1
if child > end:
break
max = child
# Среди потомков определяем максимального
for k in range(2, n + 1):
current = root * n + k
if current > end:
break
if data[current] > data[max]:
max = current
# Если максимальный потомок больше родителя
# то меняем их местами и этот потомок сам
# становится родителем
if data[root] < data[max]:
data[root], data[max] = data[max], data[root]
root = max
else:
breakВпрочем, больше — не значит, лучше. Если довести ситуацию до предела и брать N потомков для массива из N элементов, то сортировка кучей деградирует до сортировки обычным выбором. Причём это будет ещё и ухудшенная версия сортировки выбором, так как будут совершаться бессмысленные телодвижения: просейка сначала будет ставить максимум на первое место в массиве, а потом будет отправлять максимум в конец (в selection sort отправка максимума в конец происходит сразу).
Если троичная куча минимально обгоняет двоичную, то четверичная уже проигрывает. Поиск максимального потомка среди нескольких становится слишком дорогим.
Трейлер следующей серии
Итак, основной недостаток бинарной/тернарной/n-нарной кучи — невозможность прыгнуть в своей сложности выше чем
O(n log n)
. Выход из тупика — использовать в сортировке более усложнённые разновидности кучи. Через неделю ознакомимся с тем, что по этому поводу думает Эдсгер Дейкстра.
Кликните по анимации для перехода в статью со следующей сортировкой кучей
Ссылки
Heap / Пирамида
Статьи серии:
- Excel-приложение AlgoLab.xlsm
- Сортировки обменами
- Сортировки вставками
- Сортировки выбором
- Сортировки кучей: n-нарные пирамиды
- Сортировки кучей: числа Леонардо
- Сортировки кучей: слабая куча
- Сортировки кучей: декартово дерево
- Сортировки кучей: турнирное дерево
- Сортировки кучей: восходящая просейка
- Сортировки слиянием
- Сортировки распределением
- Гибридные сортировки
В приложение AlgoLab добавлена сортировка n-нарной кучей. Чтобы выбрать количество потомков, в комментарии к ячейке этой сортировки нужно указать число для n. Диапазон возможных значений — от 2 до 5 (больше нет смысла, потому что при n >= 6 анимация уже при трёх уровнях вложенности при нормальном масштабе гарантировано не помещается на экране).
В некоторых
приложениях (например, в задачах
управления оборудованием в реальном
времени) крайне важно иметь гарантию,
что время работы критических ветвей
программы даже в самом плохом случае
не превысит некоторой заданной величины.
Для таких задач использование QuickSortможет оказаться неприемлемым ввиду
названного выше недостатка этого
алгоритма – времени работы порядкаO(n2)в худшем случае. В этой ситуации следует
использовать такой алгоритм, который
работает гарантированно быстро даже в
худшем случае.
Наиболее известным
из таких алгоритмов является HeapSort,
который по-русски принято называть
пирамидальной сортировкой.
В основе алгоритма
лежит понятие пирамиды.
Массив Aназывается пирамидой, если для всех его
элементов выполнены следующие неравенства:
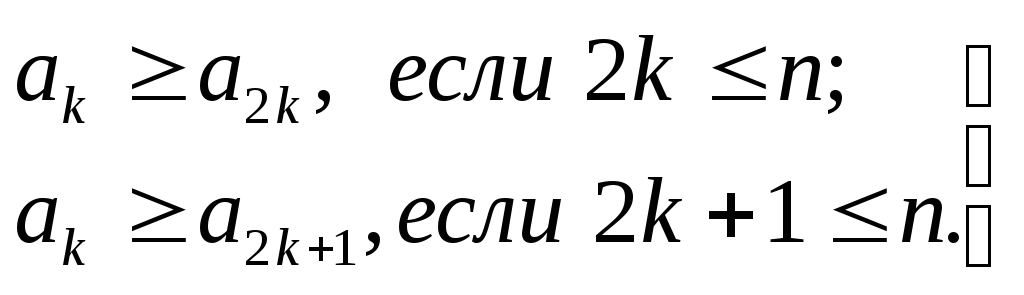
Смысл неравенств
(3.1) можно
наглядно пояснить на рис.3.1.
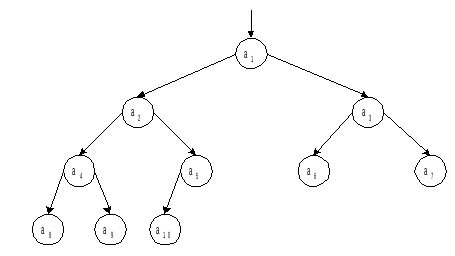
Рис. 3.1.
Представление пирамиды в виде дерева
На рисунке
массив-пирамида из 10 элементов изображен
в виде сбалансированного бинарного
дерева, вершины которого пронумерованы
сверху вниз и слева направо. При этом
элемент akвсегда будет в дереве «отцом» элементовa2kиa2k+1(если такие элементы имеются). Тогда
неравенства (3.1)
означают, что значение «отца» должно
быть не меньше, чем значения каждого из
«сыновей».
Следует, однако,
помнить, что пирамида – это не дерево,
а массив с определенными свойствами, а
изображение пирамиды в виде дерева дано
только для наглядности.
Пирамида вовсе не
обязательно является сортированным
массивом, однако она служит удобным
промежуточным результатом при сортировке.
Отметим, что первый элемент пирамиды
(a1)
всегда является максимальным элементом
массива.
Работа алгоритма
HeapSortсостоит из двух
последовательных фаз. На первой фазе
исходный массив перестраивается в
пирамиду, а на второй фазе из пирамиды
строится сортированный массив.
Основной операцией,
используемой как на первой, так и на
второй фазах сортировки, является так
называемое просеиваниеэлемента
сквозь пирамиду.
Предположим, что
неравенства (3.1)
выполнены для элементов пирамиды,
начиная с индексаk+1(т.е. для
элементовak+1,ak+2,
… ,an).
Процедура просеивания элементаakдолжна обеспечить выполнение (3.1)
дляakи при этом не нарушить этих неравенств
дляak+1,ak+2,
… ,an.
Алгоритм просеивания
заключается в следующем.
-
Если akне имеет сыновей (т.е.2k > n), то
просеивание закончено. -
Если akимеет ровно одного сына (т.е.2k = n),
то присвоитьl := nи перейти к
шагу 4. -
Сравнить значения
двух сыновей вершины ak:
еслиa2k>a2k+1,
тоl := 2k,
иначеl := 2k + 1(т.е.l– это индекс большего из
сыновейak). -
Сравнить значения
элемента akсо значением его большего сынаal:
еслиak<al,
то поменять местамиakиal. -
Присвоить k :=
lи перейти к шагу 1.
На рис. 3.1выполнение просеивания выглядит
следующим образом: вершина дерева,
значение которой меньше значения хотя
бы одного из ее сыновей, опускается
вдоль одной из ветвей дерева, пока не
займет свое законное место. При этом
все остальные вершины дерева за пределами
этой ветви остаются неизменными1.
Нетрудно видеть,
что максимально возможное число
повторений цикла в процедуре просеивания
не превышает log2n(поскольку на каждой итерации значениеkувеличивается по крайней мере
в 2 раза).
Теперь нетрудно
описать алгоритм сортировки HeapSortв целом, используя понятие просеивания
элемента.
Первая фаза
алгоритма (построение пирамиды)начинается с вычисления наибольшего
индекса элементаak,
у которого есть хотя бы один сын. Очевидно,k := n div 2.
Затем выполняется просеивание элементовak,ak–1,ak–2,
…,a2,a1.
На этом построение пирамиды завершено.
Вторая фаза
алгоритма (построение сортированного
массива)состоит из следующих шагов.
-
Поменять местами
элементы a1иan.
Напомним, что в пирамидеa1– максимальный элемент; после обмена
он будет стоять на последнем месте. -
Присвоить
n := n — 1. Тем самым мы
как бы исключаем последний элемент из
пирамиды и включаем его в сортированный
массив, который должен быть результатом
работы алгоритма. -
Поскольку после
обмена для нового элемента a1могло нарушиться свойство (3.1),
выполнить просеиваниеa1.
После этого на местеa1окажется максимальный из оставшихся
элементов пирамиды. -
Если n > 1,
то перейти к шагу 1, иначе сортировка
завершена.
На каждой итерации
второй фазы происходит исключение из
пирамиды максимального из оставшихся
в ней элементов. Этот элемент записывается
на подобающее ему место в сортированном
массиве. К концу работы алгоритма вся
пирамида превращается в сортированный
массив.
Оценим время работы
каждой фазы алгоритма HeapSort.
Первая фаза состоит изn/2операций
просеивания, каждая из которых включает
не болееlog2(n)итераций цикла. Отсюда можем легко
получить для первой фазы оценкуTмакс(n) = O(nlog(n)).
Однако эта оценка чересчур грубая. В
дальнейшем нам понадобится более точная
оценка времени работы первой фазыHeapSort. Чтобы получить такую
оценку, рассмотрим рис.3.2.
Рис. 3.2.
Число итераций просеивания при построении
пирамиды
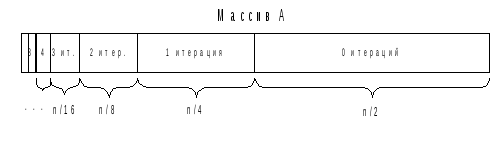
Из числа всех nэлементов массиваAпримерно половина (n/2) не имеет
сыновей и не требует просеивания (т.е.
число итераций просеивания равно 0).
Четверть элементов (n/4) имеет
сыновей, но не имеет внуков, для этих
элементов может быть выполнено не больше
одной итерации просеивания. Для одной
восьмой части элементов (n/8)
могут быть выполнены две итерации, для
одной шестнадцатой (n/16) – три
итерации и т.д. Суммарное число итераций
просеивания определится формулой:n (01/2
+ 11/4
+ 21/8
+ 31/16
+ …). Тряхнув воспоминаниями о матанализе,
можно вычислить значение суммы ряда в
скобках; это значение равно 1. Таким
образом, получаем линейную оценку
времени для первой фазы:Tмакс(n) = O(n).
Вторая фаза
алгоритма в основном представляет собой
просеивание элементов сквозь уменьшающуюся
пирамиду. Число итераций цикла можно
примерно оценить как сумму log2(n)
+ log2(n–1)
+ log2(n–2)
+ … + log2(3) + log2(3).
Поверим без доказательства, что с
точностью доO-большого эта сумма
даетTмакс(n) = O(nlog(n)).
Время работы
алгоритма в целом определяется более
трудоемкой второй фазой и удовлетворяет
оценке Tмакс(n) = O(nlog(n)).
Можно доказать, что такая же оценка
справедлива и для среднего времени
сортировки:Tср(n) = O(nlog(n)).
Таким образом,HeapSortпредставляет собой алгоритм сортировки,
который гарантирует достаточно быструю
работу даже в случае самых неудачных
исходных данных. ЭтимHeapSortвыгодно отличается отQuickSort,
который такой гарантии не дает. С другой
стороны, практика показывает, что в
среднем алгоритмHeapSortработает примерно вдвое медленнее, чемQuickSort.
Сортировка кучей, пирамидальная сортировка (англ. Heapsort) — алгоритм сортировки, использующий структуру данных двоичная куча. Это неустойчивый алгоритм сортировки с временем работы , где — количество элементов для сортировки, и использующий дополнительной памяти.
Содержание
- 1 Алгоритм
- 2 Реализация
- 3 Сложность
- 4 Пример
- 5 JSort
- 5.1 Алгоритм
- 5.2 Сложность
- 5.3 Пример
- 5.4 См. также
- 5.5 Источники информации
Алгоритм
Необходимо отсортировать массив , размером . Построим на базе этого массива за кучу для максимума. Так как максимальный элемент находится в корне, то если поменять его местами с , он встанет на своё место. Далее вызовем процедуру , предварительно уменьшив на . Она за просеет на нужное место и сформирует новую кучу (так как мы уменьшили её размер, то куча располагается с по , а элемент находится на своём месте). Повторим эту процедуру для новой кучи, только корень будет менять местами не с , а с . Делая аналогичные действия, пока не станет равен , мы будем ставить наибольшее из оставшихся чисел в конец не отсортированной части. Очевидно, что таким образом, мы получим отсортированный массив.
Реализация
- — массив, который необходимо отсортировать
- — количество элементов в нём
- — процедура, которая строит из передаваемого массива кучу для максимума в этом же массиве
- — процедура, которая просеивает вниз элемент в куче из элементов, находящихся в начале массива
fun heapSort(A : list <T>):
buildHeap(A)
heapSize = A.size
for i = 0 to n - 1
swap(A[0], A[n - 1 - i])
heapSize--
siftDown(A, 0, heapSize)
Сложность
Операция работает за . Всего цикл выполняется раз. Таким образом сложность сортировки кучей является .
Достоинства:
- худшее время работы — ,
- требует дополнительной памяти.
Недостатки:
- неустойчивая,
- на почти отсортированных данных работает столь же долго, как и на хаотических данных.
Пример
|
|
|
|
|
|
|
|
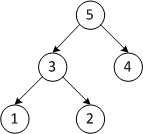
Пусть дана последовательность из элементов .
| Массив | Описание шага |
|---|---|
| 5 3 4 1 2 | Строим кучу из исходного массива |
| Первый проход | |
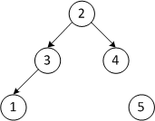
| 2 3 4 1 5 | Меняем местами первый и последний элементы |
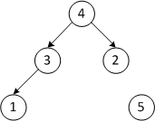
| 4 3 2 1 5 | Строим кучу из первых четырёх элементов |
| Второй проход | |
| 1 3 2 4 5 | Меняем местами первый и четвёртый элементы |
| 3 1 2 4 5 | Строим кучу из первых трёх элементов |
| Третий проход | |
| 2 1 3 4 5 | Меняем местами первый и третий элементы |
| 2 1 3 4 5 | Строим кучу из двух элементов |
| Четвёртый проход | |
| 1 2 3 4 5 | Меняем местами первый и второй элементы |
| 1 2 3 4 5 | Массив отсортирован |
JSort
JSort является модификацией сортировки кучей, которую придумал Джейсон Моррисон (Jason Morrison).
Алгоритм частично упорядочивает массив, строя на нём два раза кучу: один раз передвигая меньшие элементы влево, второй раз передвигая большие элементы вправо. Затем к массиву применяется
сортировка вставками, которая при почти отсортированных данных работает за .
Достоинства:
- В отличие от сортировки кучей, на почти отсортированных массивах работает быстрее, чем на случайных.
- В силу использования сортировки вставками, которая просматривает элементы последовательно, использование кэша гораздо эффективнее.
Недостатки:
- На длинных массивах, возникают плохо отсортированные последовательности в середине массива, что приводит к ухудшению работы сортировки вставками.
Алгоритм
Построим кучу для минимума на этом массиве.
Тогда наименьший элемент окажется на первой позиции, а левая часть массива окажется почти отсортированной, так как ей будут соответствовать верхние узлы кучи.
Теперь построим на этом же массиве кучу так, чтобы немного упорядочить правую часть массива. Эта куча должна быть кучей для максимума и быть «зеркальной» к массиву, то есть чтобы её корень соответствовал последнему элементу массива.
К получившемуся массиву применим сортировку вставками.
Сложность
Построение кучи занимает . Почти упорядоченный массив сортировка вставками может отсортировать , но в худшем случае за .
Таким образом, наихудшая оценка Jsort — .
Пример
Рассмотрим, массив =
Построим на этом массиве кучу для минимума:
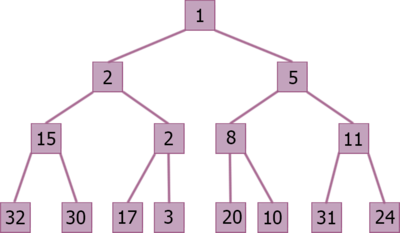
Массив выглядит следующим образом:
Заметим, что начало почти упорядочено, что хорошо скажется на использовании сортировки вставками.
Построим теперь зеркальную кучу для максимума на этом же массиве.
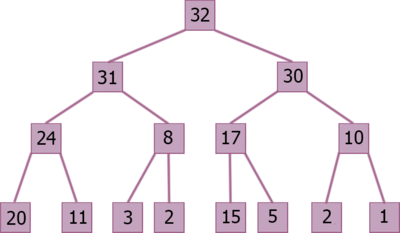
Массив будет выглядеть следующим образом:
Теперь и конец массива выглядит упорядоченным, применим сортировку вставками и получим отсортированный массив.
См. также
- Сортировка слиянием
- Быстрая сортировка
- Теорема о нижней оценке для сортировки сравнениями
Источники информации
- Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ, 2-е издание. Издательский дом «Вильямс», 2005. ISBN 5-8459-0857-4
- Wikipedia — Heapsort
- Wikipedia — JSort
- Хабрахабр — Описание сортировки кучей и JSort
- Википедия — Пирамидальная сортировка
- Подробности
- Категория: Сортировка и поиск
Пирамидальная сортировка (англ. Heapsort, «Сортировка кучей») — алгоритм сортировки, работающий в худшем, в среднем и в лучшем случае (то есть гарантированно) за O(n log n) операций при сортировке n элементов. Количество применяемой служебной памяти не зависит от размера массива (то есть, O(1)).
Может рассматриваться как усовершенствованная сортировка пузырьком, в которой элемент всплывает (min-heap) / тонет (max-heap) по многим путям.
Необходимо отсортировать массив 


![A[n - 1]](http://neerc.ifmo.ru/wiki/images/math/f/c/2/fc2868cc76a0d0e7547fbb3face8e9a1.png)




![A[0]](http://neerc.ifmo.ru/wiki/images/math/6/5/4/654231fbdf81aaea7e32bc552bf58a0b.png)
![A[0]](http://neerc.ifmo.ru/wiki/images/math/6/5/4/654231fbdf81aaea7e32bc552bf58a0b.png)
![A[n - 2]](http://neerc.ifmo.ru/wiki/images/math/5/a/7/5a72863148b487a8c30973b32027eb0f.png)
![A[n-1]](http://neerc.ifmo.ru/wiki/images/math/1/7/4/174c5d6c094683ab26f236920cfba0c2.png)
![A[n - 1]](http://neerc.ifmo.ru/wiki/images/math/f/c/2/fc2868cc76a0d0e7547fbb3face8e9a1.png)
![A[n-2]](http://neerc.ifmo.ru/wiki/images/math/3/4/d/34d7bc6f3d4794e3e848add044f324c7.png)


| Худшее время |
O(n log n) |
|---|---|
| Лучшее время |
O(n log n) |
| Среднее время |
O(n log n) |
Пусть дана последовательность из 

| Массив | Описание шага |
|---|---|
| 5 3 4 1 2 | Строим кучу из исходного массива |
| Первый проход | |
| 2 3 4 1 5 | Меняем местами первый и последний элементы |
| 4 3 2 1 5 | Строим кучу из первых четырех элементов |
| Второй проход | |
| 1 3 2 4 5 | Меняем местами первый и четвертый элементы |
| 3 1 2 4 5 | Строим кучу из первых трех элементов |
| Третий проход | |
| 2 1 3 4 5 | Меняем местами первый и третий элементы |
| 2 1 3 4 5 | Строим кучу из двух элементов |
| Четвертый проход | |
| 1 2 3 4 5 | Меняем местами первый и второй элементы |
| 1 2 3 4 5 | Массив отсортирован |
Реализация алгоритма на различных языках программирования:
C
#include <stdio.h>
#define MAXL 1000
void swap (int *a, int *b)
{
int t = *a;
*a = *b;
*b = t;
}
int main()
{
int a[MAXL], n, i, sh = 0, b = 0;
scanf ("%i", &n);
for (i = 0; i < n; ++i)
scanf ("%i", &a[i]);
while (1)
{
b = 0;
for (i = 0; i < n; ++i)
{
if (i*2 + 2 + sh < n)
{
if (a[i+sh] > a[i*2 + 1 + sh] || a[i + sh] > a[i*2 + 2 + sh])
{
if (a[i*2+1+sh] < a[i*2+2+sh])
{
swap (&a[i+sh], &a[i*2+1+sh]);
b = 1;
}
else if (a[i*2+2+sh] < a[i*2+1+sh])
{
swap (&a[i+sh],&a[i*2+2+sh]);
b = 1;
}
}
}
else if (i * 2 + 1 + sh < n)
{
if (a[i+sh] > a[i*2+1+sh])
{
swap (&a[i+sh], &a[i*2+1+sh]);
b=1;
}
}
}
if (!b) sh++;
if (sh+2==n)
break;
}
for (i = 0; i < n; ++i)
printf ("%i%c", a[i], (i!=n-1)?' ':'n');
return 0;
}
C++
#include <iterator>
template< typename Iterator >
void adjust_heap( Iterator first
, typename std::iterator_traits< Iterator >::difference_type current
, typename std::iterator_traits< Iterator >::difference_type size
, typename std::iterator_traits< Iterator >::value_type tmp )
{
typedef typename std::iterator_traits< Iterator >::difference_type diff_t;
diff_t top = current, next = 2 * current + 2;
for ( ; next < size; current = next, next = 2 * next + 2 )
{
if ( *(first + next) < *(first + next - 1) )
--next;
*(first + current) = *(first + next);
}
if ( next == size )
*(first + current) = *(first + size - 1), current = size - 1;
for ( next = (current - 1) / 2;
top > current && *(first + next) < tmp;
current = next, next = (current - 1) / 2 )
{
*(first + current) = *(first + next);
}
*(first + current) = tmp;
}
template< typename Iterator >
void pop_heap( Iterator first, Iterator last)
{
typedef typename std::iterator_traits< Iterator >::value_type value_t;
value_t tmp = *--last;
*last = *first;
adjust_heap( first, 0, last - first, tmp );
}
template< typename Iterator >
void heap_sort( Iterator first, Iterator last )
{
typedef typename std::iterator_traits< Iterator >::difference_type diff_t;
for ( diff_t current = (last - first) / 2 - 1; current >= 0; --current )
adjust_heap( first, current, last - first, *(first + current) );
while ( first < last )
pop_heap( first, last-- );
}
C++ (другой вариант)
#include <iostream>
#include <conio.h>
using namespace std;
void iswap(int &n1, int &n2)
{
int temp = n1;
n1 = n2;
n2 = temp;
}
int main()
{
int const n = 100;
int a[n];
for ( int i = 0; i < n; ++i ) { a[i] = n - i; cout << a[i] << " "; }
//заполняем массив для наглядности.
//-----------сортировка------------//
//сортирует по-возрастанию. чтобы настроить по-убыванию,
//поменяйте знаки сравнения в строчках, помеченных /*(знак)*/
int sh = 0; //смещение
bool b = false;
for(;;)
{
b = false;
for ( int i = 0; i < n; i++ )
{
if( i * 2 + 2 + sh < n )
{
if( ( a[i + sh] > /*<*/ a[i * 2 + 1 + sh] ) || ( a[i + sh] > /*<*/ a[i * 2 + 2 + sh] ) )
{
if ( a[i * 2 + 1 + sh] < /*>*/ a[i * 2 + 2 + sh] )
{
iswap( a[i + sh], a[i * 2 + 1 + sh] );
b = true;
}
else if ( a[i * 2 + 2 + sh] < /*>*/ a[ i * 2 + 1 + sh])
{
iswap( a[ i + sh], a[i * 2 + 2 + sh]);
b = true;
}
}
//дополнительная проверка для последних двух элементов
//с помощью этой проверки можно отсортировать пирамиду
//состоящую всего лишь из трех элементов
if( a[i*2 + 2 + sh] < /*>*/ a[i*2 + 1 + sh] )
{
iswap( a[i*2+1+sh], a[i * 2 +2+ sh] );
b = true;
}
}
else if( i * 2 + 1 + sh < n )
{
if( a[i + sh] > /*<*/ a[ i * 2 + 1 + sh] )
{
iswap( a[i + sh], a[i * 2 + 1 + sh] );
b = true;
}
}
}
if (!b) sh++; //смещение увеличивается, когда на текущем этапе
//сортировать больше нечего
if ( sh + 2 == n ) break;
} //конец сортировки
cout << endl << endl;
for ( int i = 0; i < n; ++i ) cout << a[i] << " ";
getch();
return 0;
}
C#
static Int32 add2pyramid(Int32[] arr, Int32 i, Int32 N)
{
Int32 imax;
Int32 buf;
if ((2 * i + 2) < N)
{
if (arr[2 * i + 1] < arr[2 * i + 2]) imax = 2 * i + 2;
else imax = 2 * i + 1;
}
else imax = 2 * i + 1;
if (imax >= N) return i;
if (arr[i] < arr[imax])
{
buf = arr[i];
arr[i] = arr[imax];
arr[imax] = buf;
if (imax < N / 2) i = imax;
}
return i;
}
static void Pyramid_Sort(Int32[] arr, Int32 len)
{
//step 1: building the pyramid
for (Int32 i = len / 2 - 1; i >= 0; --i)
{
long prev_i = i;
i = add2pyramid(arr, i, len);
if (prev_i != i) ++i;
}
//step 2: sorting
Int32 buf;
for (Int32 k = len - 1; k > 0; --k)
{
buf = arr[0];
arr[0] = arr[k];
arr[k] = buf;
Int32 i = 0, prev_i = -1;
while (i != prev_i)
{
prev_i = i;
i = add2pyramid(arr, i, k);
}
}
}
static void Main(string[] args)
{
Int32[] arr = new Int32[100];
//заполняем массив случайными числами
Random rd = new Random();
for(Int32 i = 0; i < arr.Length; ++i) {
arr[i] = rd.Next(1, 101);
}
System.Console.WriteLine("The array before sorting:");
foreach (Int32 x in arr)
{
System.Console.Write(x + " ");
}
//сортировка
Pyramid_Sort(arr, arr.Length);
System.Console.WriteLine("nnThe array after sorting:");
foreach (Int32 x in arr)
{
System.Console.Write(x + " ");
}
System.Console.WriteLine("nnPress the <Enter> key");
System.Console.ReadLine();
}
C# (другой вариант)
public class Heap<T>
{
private T[] _array; //массив сортируемых элементов
private int heapsize;//число необработанных элементов
private IComparer<T> _comparer;
public Heap(T[] a, IComparer<T> comparer){
_array = a;
heapsize = a.Length;
_comparer = comparer;
}
public void HeapSort(){
build_max_heap();//Построение пирамиды
for(int i = _array.Length - 1; i > 0; i--){
T temp = _array[0];//Переместим текущий максимальный элемент из нулевой позиции в хвост массива
_array[0] = _array[i];
_array[i] = temp;
heapsize--;//Уменьшим число необработанных элементов
max_heapify(0);//Восстановление свойства пирамиды
}
}
private int parent (int i) { return (i-1)/2; }//Индекс родительского узла
private int left (int i) { return 2*i+1; }//Индекс левого потомка
private int right (int i) { return 2*i+2; }//Индекс правого потомка
//Метод переупорядочивает элементы пирамиды при условии,
//что элемент с индексом i меньше хотя бы одного из своих потомков, нарушая тем самым свойство невозрастающей пирамиды
private void max_heapify(int i){
int l = left(i);
int r = right(i);
int lagest = i;
if (l<heapsize && _comparer.Compare(_array[l], _array[i])>0)
lagest = l;
if (r<heapsize && _comparer.Compare(_array[r], _array[lagest])>0)
lagest = r;
if (lagest != i)
{
T temp = _array[i];
_array[i] = _array[lagest];
_array[lagest] = temp;
max_heapify(lagest);
}
}
//метод строит невозрастающую пирамиду
private void build_max_heap(){
int i = (_array.Length-1)/2;
while(i>=0){
max_heapify(i);
i--;
}
}
}
public class IntComparer : IComparer<int>
{
public int Compare(int x, int y) {return x-y;}
}
public static void Main (string[] args)
{
int[] arr = Console.ReadLine().Split(' ').Select(s=>int.Parse(s)).ToArray();//вводим элементы массива через пробел
IntComparer myComparer = new IntComparer();//Класс, реализующий сравнение
Heap<int> heap = new Heap<int>(arr, myComparer);
heap.HeapSort();
}
Здесь T — любой тип, на множестве элементов которого можно ввести отношение частичного порядка.
Pascal
Вместо «SomeType» следует подставить любой из арифметических типов (например integer).
type SomeType=integer;
procedure Sort(var Arr: array of SomeType; Count: Integer);
procedure DownHeap(index, Count: integer; Current: SomeType);
//Функция пробегает по пирамиде восстанавливая ее
//Также используется для изначального создания пирамиды
//Использование: Передать номер следующего элемента в index
//Процедура пробежит по всем потомкам и найдет нужное место для следующего элемента
var
Child: Integer;
begin
while index < Count div 2 do begin
Child := (index+1)*2-1;
if (Child < Count-1) and (Arr[Child] < Arr[Child+1]) then
Child:=Child+1;
if Current >= Arr[Child] then
break;
Arr[index] := Arr[Child];
index := Child;
end;
Arr[index] := Current;
end;
//Основная функция
var
i: integer;
Current: SomeType;
begin
//Собираем пирамиду
for i := (Count div 2)-1 downto 0 do
DownHeap(i, Count, Arr[i]);
//Пирамида собрана. Теперь сортируем
for i := Count-1 downto 0 do begin
Current := Arr[i]; //перемещаем верхушку в начало отсортированного списка
Arr[i] := Arr[0];
DownHeap(0, i, Current); //находим нужное место в пирамиде для нового элемента
end;
end;
var tarr:array of SomeType;
i,n:SomeType;
begin
writeln('Введите размер массива: ');
readln(n);
setlength(tarr,n) ;//Выделяем память под динамический массив
randomize;
for i:=0 to n-1 do begin
tarr[i]:=random(500);//Генерируем случайность
write (tarr[i]:4);
end;
writeln();
writeln('Всё сортирует');
Sort(tarr,n);
for i:=0 to n-1 do begin
write (tarr[i]:4);
end;
end.
Pascal (другой вариант)
Примечание: myarray = array[1..Size] of integer; N — количество элементов массива
procedure HeapSort(var m: myarray; N: integer);
var
i: integer;
procedure Swap(var a,b:integer);
var
tmp: integer;
begin
tmp:=a;
a:=b;
b:=tmp;
end;
procedure Sort(Ns: integer);
var
i, tmp, pos, mid: integer;
begin
mid := Ns div 2;
for i := mid downto 1 do
begin
pos := i;
while pos<=mid do
begin
tmp := pos*2;
if tmp<Ns then
begin
if m[tmp+1]<m[tmp] then
tmp := tmp+1;
if m[pos]>m[tmp] then
begin
Swap(m[pos], m[tmp]);
pos := tmp;
end
else
pos := Ns;
end
else
if m[pos]>m[tmp] then
begin
Swap(m[pos], m[tmp]);
pos := Ns;
end
else
pos := Ns;
end;
end;
end;
begin
for i:=N downto 2 do
begin
Sort(i);
Swap(m[1], m[i]);
end;
end;
Pascal (третий вариант)
type TArray=array [1..10] of integer;
//процедура для перессылки записей
procedure swap(var x,y:integer);
var temp:integer;
begin
temp:=x;
x:=y;
y:=temp;
end;
//процедура приведения массива к пирамидальному виду (to pyramide)
procedure toPyr(var data:TArray; n:integer); //n - размерность массива
var i:integer;
begin
for i:=n div 2 downto 1 do begin
if 2*i<=n then if data[i]<data[2*i] then swap(data[i],data[2*i]);
if 2*i+1<=n then if data[i]<data[2*i+1] then swap(data[i],data[2*i+1]);
end;
end;
//процедура для сдвига массива влево
procedure left(var data:TArray; n:integer);
var i:integer;
temp:integer;
begin
temp:=data[1];
for i:=1 to n-1 do
data[i]:=data[i+1];
data[n]:=temp;
end;
//основная программа
var a:TArray;
i,n:integer;
begin
n:=10;//Не больше 10, потому что массив статический -
//type TArray=array [1..10] of integer;
randomize;
for i:=1 to n do begin
a[i]:=random(500);//Генерируем случайность
write (a[i]:4);
end;
for i:=n downto 1 do begin
topyr(a,i);
left(a,n);
end;
writeln();
writeln('Сортируем');
for i:=1 to n do begin
write (a[i]:4);
end;
end.
Python
def heapSort(li):
"""Сортирует список в возрастающем порядке с помощью алгоритма пирамидальной сортировки"""
def downHeap(li, k, n):
new_elem = li[k]
while 2*k+1 < n:
child = 2*k+1
if child+1 < n and li[child] < li[child+1]:
child += 1
if new_elem >= li[child]:
break
li[k] = li[child]
k = child
li[k] = new_elem
size = len(li)
for i in range(size//2-1,-1,-1):
downHeap(li, i, size)
for i in range(size-1,0,-1):
temp = li[i]
li[i] = li[0]
li[0] = temp
downHeap(li, 0, i)
Python (другой вариант)
def heapsort(s):
sl = len(s)
def swap(pi, ci):
if s[pi] < s[ci]:
s[pi], s[ci] = s[ci], s[pi]
def sift(pi, unsorted):
i_gt = lambda a, b: a if s[a] > s[b] else b
while pi*2+2 < unsorted:
gtci = i_gt(pi*2+1, pi*2+2)
swap(pi, gtci)
pi = gtci
# heapify
for i in range((sl/2)-1, -1, -1):
sift(i, sl)
# sort
for i in range(sl-1, 0, -1):
swap(i, 0)
sift(0, i)
Perl
@out=(6,4,2,8,5,3,1,6,8,4,3,2,7,9,1)
$N=@out+0;
if($N>1){
while($sh+2!=$N){
$b=undef;
for my$i(0..$N-1){
if($i*2+2+$sh<$N){
if($out[$i+$sh]gt$out[$i*2+1+$sh] || $out[$i+$sh]gt$out[$i*2+2+$sh]){
if($out[$i*2+1+$sh]lt$out[$i*2+2+$sh]){
($out[$i*2+1+$sh],$out[$i+$sh])=($out[$i+$sh],$out[$i*2+1+$sh]);
$b=1;
}elsif($out[$i*2+2+$sh]lt$out[$i*2+1+$sh]){
($out[$i*2+2+$sh],$out[$i+$sh])=($out[$i+$sh],$out[$i*2+2+$sh]);
$b=1;
}
}elsif($out[$i*2+2+$sh]lt$out[$i*2+1+$sh]){
($out[$i*2+1+$sh],$out[$i*2+2+$sh])=($out[$i*2+2+$sh],$out[$i*2+1+$sh]);
$b=1;
}
}elsif($i*2+1+$sh<$N && $out[$i+$sh]gt$out[$i*2+1+$sh]){
($out[$i+$sh],$out[$i*2+1+$sh])=($out[$i*2+1+$sh],$out[$i+$sh]);
$b=1;
}
}
++$sh if!$b;
last if$sh+2==$N;
}
}
Java
/**
* Класс для сортировки массива целых чисел с помощью кучи.
* Методы в классе написаны в порядке их использования. Для сортировки
* вызывается статический метод sort(int[] a)
*/
class HeapSort {
/**
* Размер кучи. Изначально равен размеру сортируемого массива
*/
private static int heapSize;
/**
* Сортировка с помощью кучи.
* Сначала формируется куча:
* @see HeapSort#buildHeap(int[])
* Теперь максимальный элемент массива находится в корне кучи. Его нужно
* поменять местами с последним элементом и убрать из кучи (уменьшить
* размер кучи на 1). Теперь в корне кучи находится элемент, который раньше
* был последним в массиве. Нужно переупорядочить кучу так, чтобы
* выполнялось основное условие кучи - a[parent]>=a[child]:
* @see #heapify(int[], int)
* После этого в корне окажется максимальный из оставшихся элементов.
* Повторить до тех пор, пока в куче не останется 1 элемент
*
* @param a сортируемый массив
*/
public static void sort(int[] a) {
buildHeap(a);
while (heapSize > 1) {
swap(a, 0, heapSize - 1);
heapSize--;
heapify(a, 0);
}
}
/**
* Построение кучи. Поскольку элементы с номерами начиная с a.length / 2 + 1
* это листья, то нужно переупорядочить поддеревья с корнями в индексах
* от 0 до a.length / 2 (метод heapify вызывать в порядке убывания индексов)
*
* @param a - массив, из которого формируется куча
*/
private static void buildHeap(int[] a) {
heapSize = a.length;
for (int i = a.length / 2; i >= 0; i--) {
heapify(a, i);
}
}
/**
* Переупорядочивает поддерево кучи начиная с узла i так, чтобы выполнялось
* основное свойство кучи - a[parent] >= a[child].
*
* @param a - массив, из которого сформирована куча
* @param i - корень поддерева, для которого происходит переупорядосивание
*/
private static void heapify(int[] a, int i) {
int l = left(i);
int r = right(i);
int largest = i;
if (l < heapSize && a[i] < a[l]) {
largest = l;
}
if (r < heapSize && a[largest] < a[r]) {
largest = r;
}
if (i != largest) {
swap(a, i, largest);
heapify(a, largest);
}
}
/**
* Возвращает индекс правого потомка текущего узла
*
* @param i индекс текущего узла кучи
* @return индекс правого потомка
*/
private static int right(int i) {
return 2 * i + 1;
}
/**
* Возвращает индекс левого потомка текущего узла
*
* @param i индекс текущего узла кучи
* @return индекс левого потомка
*/
private static int left(int i) {
return 2 * i + 2;
}
/**
* Меняет местами два элемента в массиве
*
* @param a массив
* @param i индекс первого элемента
* @param j индекс второго элемента
*/
private static void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
Достоинства
- Имеет доказанную оценку худшего случая
.
- Сортирует на месте, то есть требует всего O(1) дополнительной памяти (если дерево организовывать так, как показано выше).
Недостатки
- Сложен в реализации.
- Неустойчив — для обеспечения устойчивости нужно расширять ключ.
- На почти отсортированных массивах работает столь же долго, как и на хаотических данных.
- На одном шаге выборку приходится делать хаотично по всей длине массива — поэтому алгоритм плохо сочетается с кэшированием и подкачкой памяти.
- Методу требуется «мгновенный» прямой доступ; не работает на связанных списках и других структурах памяти последовательного доступа.
Сортировка слиянием при расходе памяти O(n) быстрее (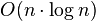
Из-за сложности алгоритма выигрыш получается только на больших n. На небольших n (до нескольких тысяч) быстрее сортировка Шелла.
При написании статьи были использованы открытые источники сети интернет :
Wikipedia
Kvodo
Youtube
Метод пирамидальной сортировки, изобретенный Д. Уилльямсом, является улучшением традиционных сортировок с помощью дерева.
Пирамидой (кучей) называется двоичное дерево такое, что
a[i] ≤ a[2i+1];
a[i] ≤ a[2i+2].
Подробнее
a[0] — минимальный элемент пирамиды.
Общая идея пирамидальной сортировки заключается в том, что сначала строится пирамида из элементов исходного массива, а затем осуществляется сортировка элементов.
Выполнение алгоритма разбивается на два этапа.
1 этап Построение пирамиды. Определяем правую часть дерева, начиная с n/2-1 (нижний уровень дерева). Берем элемент левее этой части массива и просеиваем его сквозь пирамиду по пути, где находятся меньшие его элементы, которые одновременно поднимаются вверх; из двух возможных путей выбираете путь через меньший элемент.
Например, массив для сортировки
24, 31, 15, 20, 52, 6
Расположим элементы в виде исходной пирамиды; номер элемента правой части (6/2-1)=2 — это элемент 15.
Результат просеивания элемента 15 через пирамиду.
Следующий просеиваемый элемент – 1, равный 31.
Затем – элемент 0, равный 24.
Разумеется, полученный массив еще не упорядочен. Однако процедура просеивания является основой для пирамидальной сортировки. В итоге просеивания наименьший элемент оказывается на вершине пирамиды.
2 этап Сортировка на построенной пирамиде. Берем последний элемент массива в качестве текущего. Меняем верхний (наименьший) элемент массива и текущий местами. Текущий элемент (он теперь верхний) просеиваем сквозь n-1 элементную пирамиду. Затем берем предпоследний элемент и т.д.
Продолжим процесс. В итоге массив будет отсортирован по убыванию.
Реализация пирамидальной сортировки на Си
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <stdio.h>
#include <stdlib.h>
// Функция «просеивания» через кучу — формирование кучи
void siftDown(int *numbers, int root, int bottom)
{
int maxChild; // индекс максимального потомка
int done = 0; // флаг того, что куча сформирована
// Пока не дошли до последнего ряда
while ((root * 2 <= bottom) && (!done))
{
if (root * 2 == bottom) // если мы в последнем ряду,
maxChild = root * 2; // запоминаем левый потомок
// иначе запоминаем больший потомок из двух
else if (numbers[root * 2] > numbers[root * 2 + 1])
maxChild = root * 2;
else
maxChild = root * 2 + 1;
// если элемент вершины меньше максимального потомка
if (numbers[root] < numbers[maxChild])
{
int temp = numbers[root]; // меняем их местами
numbers[root] = numbers[maxChild];
numbers[maxChild] = temp;
root = maxChild;
}
else // иначе
done = 1; // пирамида сформирована
}
}
// Функция сортировки на куче
void heapSort(int *numbers, int array_size)
{
// Формируем нижний ряд пирамиды
for (int i = (array_size / 2); i >= 0; i—)
siftDown(numbers, i, array_size — 1);
// Просеиваем через пирамиду остальные элементы
for (int i = array_size — 1; i >= 1; i—)
{
int temp = numbers[0];
numbers[0] = numbers[i];
numbers[i] = temp;
siftDown(numbers, 0, i — 1);
}
}
int main()
{
int a[10];
// Заполнение массива случайными числами
for (int i = 0; i<10; i++)
a[i] = rand() % 20 — 10;
// Вывод элементов массива до сортировки
for (int i = 0; i<10; i++)
printf(«%d «, a[i]);
printf(«n»);
heapSort(a, 10); // вызов функции сортировки
// Вывод элементов массива после сортировки
for (int i = 0; i<10; i++)
printf(«%d «, a[i]);
printf(«n»);
getchar();
return 0;
}
Результат выполнения
Анализ алгоритма пирамидальной сортировки
Несмотря на некоторую внешнюю сложность, пирамидальная сортировка является одной из самых эффективных. Алгоритм сортировки эффективен для больших n. В худшем случае требуется n·log2n шагов, сдвигающих элементы. Среднее число перемещений примерно равно
(n/2)·log2n,
и отклонения от этого значения относительно невелики.
Назад: Алгоритмы сортировки и поиска
Получив целочисленный массив, отсортируйте его, используя алгоритм пирамидальной сортировки в C, C++, Java и Python.
Обзор Heapsort
Heapsort — это на месте, алгоритм сортировки на основе сравнения и может рассматриваться как улучшенный сортировка выбором поскольку он делит ввод на отсортированную и несортированную области. Он итеративно сжимает несортированную область, извлекая наибольший/наименьший элемент и перемещая его в отсортированную область. Улучшение состоит в использовании структуры данных кучи, а не в поиске с линейным временем для нахождения максимума. Heapsort не обеспечивает стабильной сортировки, что означает, что реализация не сохраняет входной порядок одинаковых элементов в отсортированном выходе. Как правило, медленнее, чем другие O(n.log(n)) алгоритмы сортировки, такие как быстрая сортировка, Сортировка слиянием.
Алгоритм heapsort можно разделить на две части:
- На первом этапе из входных данных строится куча. Мы можем сделать это в O(n) время.
- На втором этапе создается отсортированный массив путем многократного удаления самого большого/наименьшего элемента из кучи (корень кучи) и вставки его в массив. Куча обновляется(heapify-down вызывается на корневом узле) после каждого удаления для сохранения свойства кучи. Как только все элементы будут удалены из кучи, мы получим отсортированный массив. Это делается в O(n.log(n)) время, так как нам нужно поп
nэлементы, где каждое удаление включает в себя постоянный объем работы, а одна операция heapify занимает O(log(n)) время.
Как построить кучу?
Наивным решением было бы начать с пустой кучи и многократно вставлять в нее каждый элемент входного списка. Проблема с этим подходом в том, что он работает в O(n.log(n)) время на входе, содержащем n элементы, как он выполняет n вставки в O(log(n)) стоимость каждого.
Мы можем построить кучу в O(n) время, произвольно помещая входные элементы в массив кучи. Затем, начиная с последнего внутреннего узла кучи (присутствует по индексу (n-2)/2 в массиве), вызовите процедуру heapify на каждом узле до корневого узла (до индекса 0). Поскольку процедура heapify ожидает, что левый и правый дочерние элементы узла будут кучами, начните с последнего внутреннего узла (поскольку конечные узлы уже являются кучами) и двигайтесь вверх уровень за уровнем.
Можно утверждать, что основная операция heapify с кучей выполняется в O(log(n)) время, и мы вызываем heapify примерно n/2 times (по одному на каждый внутренний узел). Таким образом, временная сложность приведенного выше решения равна O(n.log(n)). Однако оказалось, что анализ не плотно.
Когда вызывается heapify, время выполнения зависит от того, насколько далеко элемент может сместиться в дереве до того, как процесс завершится. Другими словами, это зависит от высоты элемента в куче. В худшем случае элемент может опуститься на конечный уровень. Считаем проделанную работу уровень за уровнем.
- Есть
2hузлы на самом нижнем уровне, но мы не вызываем heapify ни для одного из них, поэтому работа равна 0. - Есть
2(h-1)узлы на следующем уровне, и каждый из них может сместиться на 1 уровень вниз. - На 3-м уровне снизу находятся
2(h-2)узлов, и каждый из них может спуститься на 2 уровня вниз и продолжить…
Как мы видим, не все операции heapify O(log(n)), и именно поэтому, проведя тщательный анализ, мы можем получить O(n) время.
Практикуйте этот алгоритм
1. Реализация Heapsort на месте
Heapsort можно выполнять на месте. Мы можем сделать это с помощью
- Использование максимальной кучи вместо минимальной кучи (для сортировки по возрастанию),
- Использование входного массива для построения кучи (вместо использования кучи собственного хранилища)
Идея состоит в том, чтобы разделить массив на две части — кучу и отсортированный массив. По мере того, как каждая операция выталкивания освобождает место в конец массива в двоичной куче, перемещайте извлеченный элемент в свободное пространство. Таким образом, первый извлеченный элемент (максимальный элемент) переместится в последнюю позицию в массиве, второй извлеченный элемент (следующий максимальный элемент) переместится в предпоследнюю позицию в массиве и так далее… наконец, когда все элементы вытолкнут из кучи, мы получим массив, отсортированный по возрастанию.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 |
#include <stdio.h> // сохраняет размер кучи int end; void swap(int *x, int *y) { *x = (*x**y) / (*y = *x); } // вернуть левого потомка `A[i]` int LEFT(int i) { return (2*i + 1); } // вернуть правого потомка `A[i]` int RIGHT(int i) { return (2*i + 2); } // Рекурсивный алгоритм heapify-down // узел с индексом `i` и два его прямых потомка // нарушает свойство кучи void heapify(int A[], int i) { // получить левый и правый потомки узла с индексом `i` int left = LEFT(i); int right = RIGHT(i); // сравниваем `A[i]` с его левым и правым дочерними элементами // и находим наибольшее значение int largest = i; if (left < end && A[left] > A[i]) { largest = left; } if (right < end && A[right] > A[largest]) { largest = right; } // поменяться местами с потомком, имеющим большее значение и // вызываем heapify для дочернего элемента if (largest != i) { swap(&A[i], &A[largest]); heapify(A, largest); } } // Переупорядочиваем элементы массива для создания максимальной кучи void BuildHeap(int A[]) { // вызовите heapify, начиная с последнего внутреннего узла, все // путь до корневого узла int i = (end — 2) / 2; while (i >= 0) { heapify(A, i—); } } void heapsort(int A[], int n) { // инициализируем размер кучи как общее количество элементов в массиве end = n; // переупорядочиваем элементы массива для создания максимальной кучи BuildHeap(A); /* Следующий цикл поддерживает, что `A[0, end-1]` это куча, и каждый элемент за концом больше, чем все до него (так что `A[end: n-1]` находится в отсортированном порядке) */ // делаем до тех пор, пока в куче не останется только один элемент while (end != 1) { // перемещаем следующий наибольший элемент в конец // массив (перемещает его перед отсортированными элементами) swap(&A[0], &A[end — 1]); // уменьшить размер кучи на 1 end—; // вызываем heapify на корневом узле, так как своп уничтожен // свойство кучи heapify(A, 0); } } // Реализация алгоритма Heapsort на C int main(void) { int A[] = { 6, 4, 7, 1, 9, —2 }; int n = sizeof(A) / sizeof(A[0]); // выполняем иерархическую сортировку массива heapsort(A, n); // печатаем отсортированный массив for (int i = 0; i < n; i++) { printf(«%d «, A[i]); } return 0; } |
Скачать Выполнить код
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 |
#include <iostream> #include <vector> using namespace std; class PriorityQueue { // вернуть левого потомка `A[i]` int LEFT(int i) { return (2*i + 1); } // вернуть правого потомка `A[i]` int RIGHT(int i) { return (2*i + 2); } // Рекурсивный алгоритм heapify-down // узел с индексом `i` и два его прямых потомка // нарушает свойство кучи void heapify(vector<int> &A, int i, int size) { // получить левый и правый потомки узла с индексом `i` int left = LEFT(i); int right = RIGHT(i); int largest = i; // сравниваем `A[i]` с его левым и правым дочерними элементами // и находим наибольшее значение if (left < size && A[left] > A[i]) { largest = left; } if (right < size && A[right] > A[largest]) { largest = right; } // поменяться местами с потомком, имеющим большее значение и // вызовите heapify-down для дочернего элемента if (largest != i) { swap(A[i], A[largest]); heapify(A, largest, size); } } public: // Конструктор (Build-Heap) PriorityQueue(vector<int> &A, int n) { // вызовите heapify, начиная с последнего внутреннего узла, все // путь до корневого узла int i = (n — 2) / 2; while (i >= 0) { heapify(A, i—, n); } } // Функция для удаления элемента с наивысшим приоритетом (присутствует в корне) int pop(vector<int> &A, int size) { // если в куче нет элементов if (size <= 0) { return —1; } int top = A[0]; // заменяем корень кучи последним элементом // массива A[0] = A[size—1]; // вызовите heapify-down на корневом узле heapify(A, 0, size — 1); return top; } }; // Функция для выполнения пирамидальной сортировки массива `A` размера `n` void heapsort(vector<int> &A, int n) { // строим приоритетную очередь и инициализируем ее заданным массивом PriorityQueue pq(A, n); // несколько раз извлекаем из кучи, пока она не станет пустой while (n > 0) { A[n — 1] = pq.pop(A, n); n—; } } // Реализация алгоритма Heapsort на C++ int main() { vector<int> A = { 6, 4, 7, 1, 9, —2 }; int n = A.size(); // выполняем иерархическую сортировку массива heapsort(A, n); // печатаем отсортированный массив for (int i = 0; i < n; i++) { cout << A[i] << » «; } return 0; } |
Скачать Выполнить код
результат:
-2 1 4 6 7 9
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 |
import java.util.Arrays; class Main { // вернуть левого потомка `A[i]` private static int LEFT(int i) { return (2*i + 1); } // вернуть правого потомка `A[i]` private static int RIGHT(int i) { return (2*i + 2); } // Вспомогательная функция для замены двух индексов в массиве private static void swap(int[] A, int i, int j) { int temp = A[i]; A[i] = A[j]; A[j] = temp; } // Рекурсивный алгоритм heapify-down. Узел с индексом `i` и // два его прямых потомка нарушают свойство кучи private static void heapify(int[] A, int i, int size) { // получить левый и правый потомки узла с индексом `i` int left = LEFT(i); int right = RIGHT(i); int largest = i; // сравниваем `A[i]` с его левым и правым дочерними элементами // и находим наибольшее значение if (left < size && A[left] > A[i]) { largest = left; } if (right < size && A[right] > A[largest]) { largest = right; } // поменяться местами с потомком, имеющим большее значение и // вызовите heapify-down для дочернего элемента if (largest != i) { swap(A, i, largest); heapify(A, largest, size); } } // Функция для удаления элемента с наивысшим приоритетом (присутствует в корне) public static int pop(int[] A, int size) { // если в куче нет элементов if (size <= 0) { return —1; } int top = A[0]; // заменяем корень кучи последним элементом // массива A[0] = A[size—1]; // вызовите heapify-down на корневом узле heapify(A, 0, size — 1); return top; } // Функция для выполнения пирамидальной сортировки массива `A` размера `n` public static void heapsort(int[] A) { // строим приоритетную очередь и инициализируем ее заданным массивом int n = A.length; // Build-heap: вызывать heapify, начиная с последнего внутреннего // узел до корневого узла int i = (n — 2) / 2; while (i >= 0) { heapify(A, i—, n); } // несколько раз извлекаем из кучи, пока она не станет пустой while (n > 0) { A[n — 1] = pop(A, n); n—; } } // Реализация алгоритма Heapsort в Java public static void main(String[] args) { int[] A = { 6, 4, 7, 1, 9, —2 }; // выполняем иерархическую сортировку массива heapsort(A); // печатаем отсортированный массив System.out.println(Arrays.toString(A)); } } |
Скачать Выполнить код
результат:
[-2, 1, 4, 6, 7, 9]
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 |
# возвращает левого потомка `A[i]` def LEFT(i): return 2*i + 1 # возвращает правого потомка `A[i]` def RIGHT(i): return 2*i + 2 # Вспомогательная функция для замены двух индексов в списке def swap(A, i, j): temp = A[i] A[i] = A[j] A[j] = temp # Рекурсивный алгоритм heapify-down. Узел с индексом `i` и # два его прямых потомка нарушают свойство кучи def heapify(A, i, size): # получает левый и правый потомки узла с индексом `i` left = LEFT(i) right = RIGHT(i) largest = i # сравнивает `A[i]` с его левым и правым дочерними элементами # и найти наибольшее значение if left < size and A[left] > A[i]: largest = left if right < size and A[right] > A[largest]: largest = right # поменяться местами с ребенком, имеющим большую ценность и # вызывает heapify-down для ребенка if largest != i: swap(A, i, largest) heapify(A, largest, size) # Функция удаления элемента с наивысшим приоритетом (присутствует в корне) def pop(A, size): #, если в куче нет элементов if size <= 0: return —1 top = A[0] # заменить корень кучи последним элементом # списка A[0] = A[size — 1] # вызывает heapify-down на корневом узле heapify(A, 0, size — 1) return top # Функция для выполнения пирамидальной сортировки в списке `A` размера `n` def heapsort(A): # создает приоритетную очередь и инициализирует ее заданным списком n = len(A) # Build-heap: вызывать heapify, начиная с последнего внутреннего # Узел # вплоть до корневого узла i = (n — 2) // 2 while i >= 0: heapify(A, i, n) i = i — 1 # постоянно выталкивается из кучи, пока она не станет пустой while n: A[n — 1] = pop(A, n) n = n — 1 if __name__ == ‘__main__’: A = [6, 4, 7, 1, 9, —2] # выполняет пирамидальную сортировку списка heapsort(A) # распечатать отсортированный список print(A) |
Скачать Выполнить код
результат:
[-2, 1, 4, 6, 7, 9]
Временная сложность приведенного выше алгоритма равна O(n.log(n)), куда n является входным размером и требует O(n) неявное пространство для стека вызовов.
2. Неуместная реализация Heapsort
The неуместный Алгоритм heapsort может быть реализован на C++ и Java следующим образом:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 |
#include <iostream> #include <vector> using namespace std; // Класс для хранения узла минимальной кучи class PriorityQueue { // массив для хранения элементов кучи int *A; // сохраняет текущий размер кучи unsigned size; // вернуть левого потомка `A[i]` int LEFT(int i) { return (2*i + 1); } // вернуть правого потомка `A[i]` int RIGHT(int i) { return (2*i + 2); } // Рекурсивный алгоритм heapify-down // узел с индексом `i` и два его прямых потомка // нарушает свойство кучи void heapify(int i) { // получить левый и правый потомки узла с индексом `i` int left = LEFT(i); int right = RIGHT(i); int smallest = i; // сравниваем `A[i]` с его левым и правым дочерними элементами // и находим наименьшее значение if (left < size && A[left] < A[i]) { smallest = left; } if (right < size && A[right] < A[smallest]) { smallest = right; } // поменяться местами с дочерним элементом с меньшим значением и // вызовите heapify-down для дочернего элемента if (smallest != i) { swap(A[i], A[smallest]); heapify(smallest); } } public: // Конструктор (Build-Heap) PriorityQueue(vector<int> &arr, int n) { // выделяем память в кучу и инициализируем ее заданным массивом A = new int[n]; for (int i = 0; i < n; i++) { A[i] = arr[i]; } // устанавливаем объем кучи равным размеру массива size = n; // вызовите heapify, начиная с последнего внутреннего узла, все // путь до корневого узла int i = (n — 2) / 2; while (i >= 0) { heapify(i—); } } // Деструктор ~PriorityQueue() { // освобождаем память, используемую узлами кучи delete[] A; } // Функция для проверки, пуста ли куча или нет int empty() { return size == 0; } // Функция для удаления элемента с наивысшим приоритетом (присутствует в корне) int pop() { // если в куче нет элементов if (size <= 0) { return —1; } int top = A[0]; // заменяем корень кучи последним элементом // массива A[0] = A[size—1]; // уменьшить размер кучи на 1 size—; // вызовите heapify-down на корневом узле heapify(0); return top; } }; // Функция для выполнения пирамидальной сортировки массива `A` размера `n` void heapsort(vector<int> &A, int n) { // строим приоритетную очередь и инициализируем ее заданным массивом PriorityQueue pq(A, n); int i = 0; // несколько раз извлекаем из кучи, пока она не станет пустой while (!pq.empty()) { A[i++] = pq.pop(); } } // Реализация алгоритма Heapsort на C++ int main() { vector<int> A = { 6, 4, 7, 1, 9, —2 }; int n = A.size(); // выполняем иерархическую сортировку массива heapsort(A, n); // печатаем отсортированный массив for (int i = 0; i < n; i++) { cout << A[i] << » «; } return 0; } |
Скачать Выполнить код
результат:
-2 1 4 6 7 9
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 |
import java.util.Arrays; // Класс для хранения узла минимальной кучи class PriorityQueue { // массив для хранения элементов кучи private static int[] A = null; // сохраняет текущий размер кучи private static int size; // вернуть левого потомка `A[i]` private static int LEFT(int i) { return (2*i + 1); } // вернуть правого потомка `A[i]` private static int RIGHT(int i) { return (2*i + 2); } // Рекурсивный алгоритм heapify-down. Узел с индексом `i` и // два его прямых потомка нарушают свойство кучи private static void heapify(int i) { // получить левый и правый потомки узла с индексом `i` int left = LEFT(i); int right = RIGHT(i); int smallest = i; // сравниваем `A[i]` с его левым и правым дочерними элементами // и находим наименьшее значение if (left < size && A[left] < A[i]) { smallest = left; } if (right < size && A[right] < A[smallest]) { smallest = right; } // поменяться местами с дочерним элементом с меньшим значением и // вызовите heapify-down для дочернего элемента if (smallest != i) { swap(A, i, smallest); heapify(smallest); } } // Вспомогательная функция для замены двух индексов в массиве private static void swap(int[] A, int i, int j) { int temp = A[i]; A[i] = A[j]; A[j] = temp; } // Конструктор (Build-Heap) PriorityQueue(int[] arr) { // выделяем память в кучу и инициализируем ее заданным массивом A = Arrays.copyOf(arr, arr.length); // устанавливаем объем кучи равным размеру массива size = arr.length; // вызовите heapify, начиная с последнего внутреннего узла, все // путь до корневого узла int i = (arr.length — 2) / 2; while (i >= 0) { heapify(i—); } } // Функция для проверки, пуста ли куча или нет public static boolean empty() { return size == 0; } // Функция для удаления элемента с наивысшим приоритетом (присутствует в корне) public static int pop() { // если в куче нет элементов if (size <= 0) { return —1; } int top = A[0]; // заменяем корень кучи последним элементом // массива A[0] = A[size—1]; // уменьшить размер кучи на 1 size—; // вызовите heapify-down на корневом узле heapify(0); return top; } } class Main { // Функция для выполнения пирамидальной сортировки массива `A` размера `n` public static void heapsort(int[] A) { // строим приоритетную очередь и инициализируем ее заданным массивом PriorityQueue pq = new PriorityQueue(A); // несколько раз извлекаем из кучи, пока она не станет пустой int i = 0; while (!pq.empty()) { A[i++] = pq.pop(); } } // Реализация алгоритма Heapsort в Java public static void main(String[] args) { int[] A = { 6, 4, 7, 1, 9, —2 }; // выполняем иерархическую сортировку массива heapsort(A); // печатаем отсортированный массив System.out.println(Arrays.toString(A)); } } |
Скачать Выполнить код
результат:
[-2, 1, 4, 6, 7, 9]
Временная сложность приведенного выше алгоритма равна O(n.log(n)), а вспомогательное пространство, используемое программой, равно O(n), куда n это размер ввода.
Упражнение: Сортировка элементов по убыванию с помощью heapsort
Использованная литература:
1. https://en.wikipedia.org/wiki/Heapsort
2. https://stackoverflow.com/questions/9755721/how-can-building-a-heap-be-on-time-complexity
Спасибо за чтение.
Пожалуйста, используйте наш онлайн-компилятор размещать код в комментариях, используя C, C++, Java, Python, JavaScript, C#, PHP и многие другие популярные языки программирования.
Как мы? Порекомендуйте нас своим друзьям и помогите нам расти. Удачного кодирования 🙂
Алгоритмы сортировки
Пирамидальная сортировка
Пирамидальная сортировка основана на использовании структуры данных пирамида (heap). Это структура данных представляет собой бинарное дерево. Каждый узел дерева соответствует элементу массива. Последний уровень заполняется слева направо.
Рассмотрим вспомогательные методы, которые использует пирамидальная сортировка.
Метод Parent(i) возвращает индекс родительского узла i:
private int parent(int i){
return i/2;
}
Метод left(i) — получение индекса левого дочернего узла, где i — родительский узел:
private int left(int i){
return 2*i;
}
Метод right(i) — получение индекса правого дочернего узла, где i — родительский узел:
private int right(int i){
return 2*i + 1;
}
Замечание:
Метод parent(i) возвращает наименьшее целое число, при передаче ему нечетного числа.
- Невозрастающая пирамида
- Пирамида является невозрастающей в том случае, когда значения дочерних узлов меньше, либо равны значению родительского узла.
- Неубывающая пирамида
- Пирамида является неубывающей в том случае, когда значения дочерних узлов больше, либо равны значению родительского узла.
Метод heapify(A,i) — поддерживает свойство невозрастающей пирамиды:
private void heapify(Integer i){
int largest;
int left = left(i);
int right = right(i);
if ((left < heapSize) && (arr[left] > arr[i])){
largest = left;
}
else{
largest = i;
}
if ((right < heapSize) && (arr[right] > arr[largest])){
largest = right;
}
if (i != largest){
int temp = arr[i];
arr[i] = arr[largest];
arr[largest] = temp;
this.heapify(largest);
}
}
В методе есть дополнительные проверки, типа (left < heapSize) и (right < heapSize). Методы left(i) и right(i) могут вернуть такой индекс, который не входит в пирамиду. Метод является рекурсивным, после обмена значениями дочерних узлов и родительского узла, повторно вызывается этот же метод, которому передается индекс узла с наибольшим значением.
Конструктор Heap(A) — создает невозрастающую пирамиду из элементов массива:
public Heap(Integer A[]){
arr = A;
heapSize = A.length;
// создаем пирамиду
for (int i = arr.length/2 - 1; i >= 0; i--){
heapify(i);
}
}
Функция heapSort(A) — пирамидальная сортировка.:
public void heapSort(){
int arrLength = heapSize;
for (int i = arrLength-1; i >= 1; i--){
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
--heapSize;
heapify(0);
}
}
В теле цикла значениями обмениваются корневой узел пирамиды arr[0] и последний элемент пирамиды (leaf node). После чего, размер пирамиды уменьшается, узел таким образом отсекается, и вызывается метод поддержания свойства невозрастания пирамиды heapify(0). Вызов метод нужен потому, что в корне пирамиды после обмена содержится наименьшее значение.
Анализ времени выполнения алгоритма
Метод left(i) выполняется очень быстро, путем битового сдвига числа i влево на одну позицию:
i = 3 = 11; i = 2*3 = 110 i = 8 = 1000 i = 8*2 = 10000
Метод right(i) тоже выполняется очень быстро, путем битового сдвига числа i влево на одну позицию и установки младшего бита в единицу:
i = 3 = 11; i = 2*3 + 1 = 111 i = 8 = 1000 i = 8*2 + 1 = 1001
Время работы метода heapify(i) в заданном узле i, вычисляется как время theta (1), необходимое для исправления отношений между элементами arr[i], arr[left(i)] или arr[right(i)], плюс время работы метода с поддеревом, корень которого находится в одном из дочерних узлов i. Время работы метода heapify(i) c узлом i, находящимся на высоте h, можно выразить как О(h) или O(lgn);
Высота узла определяется как количество его предков. Высоту дерева определяют по высоте его узлов листьев (leaf nodes).
Время работы метода heapsort() равно О(nlgn), поскольку вызов метода Heap() требует времени O(n), а каждый из n-1 вызовов метода heapify — времени O(lgn)