ГДЗ #1

51. Перевозки пассажиров между населенными пунктами А, Б, В. Г, Д осуществляют три компании, представившие стоимость своих услуг в табличной форме. Какая компания обеспечивает минимальную стоимость проезда из A в Б?
На этой странице вы сможете найти и списать готовое домешнее задание (ГДЗ) для школьников по предмету Информатика, которые посещают 9 класс из книги или рабочей тетради под названием/издательством «Рабочая тетрадь», которая была написана автором/авторами: Босова. ГДЗ представлено для списывания совершенно бесплатно и в открытом доступе.

§ 1.4. Табличные информационные модели ГДЗ по Информатике 9 класс. Босова.
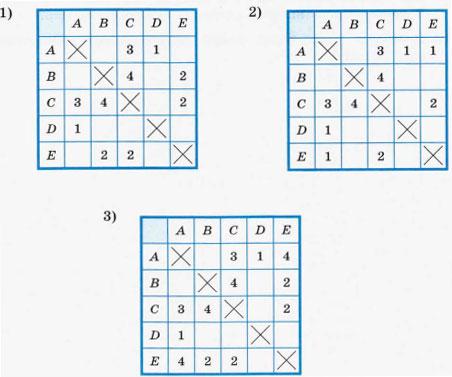
Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость перевозок между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними. Стоимость перевозок по маршруту складывается из стоимостей перевозок между соседними станциями. Перевозки между населёнными пунктами А, В, С, В, Е осуществляют три компании, представившие стоимость своих услуг в табличной форме. Какая компания обеспечивает минимальную стоимость перевозок из А в В?

Ответ
Для большей наглядности перейдем от таблиц к графам:

Минимальная стоимость у 1 компании
ACB = 3 + 4 = 7
Минимальная стоимость у 2 компании
ACB = 3 + 4 = 7
AECB = 1 + 2 + 4 = 7
Минимальная стоимость у 3 компании
ACB = 3 + 4 = 7
AECB = 4 + 2 + 4 = 10
AEB = 4 + 2 = 6
Ответ:
Третья компания.
OBRAZOVALKA.COM
OBRAZOVALKA.COM — образовательный портал
Наш сайт это площадка для образовательных консультаций, вопросов и ответов для школьников и студентов .
На вопросы могут отвечать также любые пользователи, в том числе и педагоги.
Консультацию по вопросам и домашним заданиям может получить любой школьник или студент.
Оглавление:
- 1 Ответы (решебник) к учебнику по Информатике — 9 класс, параграф 1.4 — Босова Л.Л., Босова А.Ю., задания 1-10
- 1.1 Глава 1. МОДЕЛИРОВАНИЕ И ФОРМАЛИЗАЦИЯ
- 1.2 §1.4.Табличные информационные модели ГДЗ, Информатика 9 класс Босова ответы на «Вопросы и задания»
- 1.3 1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.
- 1.4 2. Какие преимущества обеспечивают табличные информационные модели по сравнению со словесными описаниями? Приведите пример
- 1.5 3. Примеры табличный информационных моделей:
- 1.6 4. К какому типу относится таблица «Табель успеваемости», расположенная в конце вашего дневника?
- 1.7 5. Узнайте, в каких случаях в ячейку таблицы ставится знак «х». Почему мы использовали этот знак в таблице (пример 2)?
- 1.8 6. Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 1 камень, а во второй — 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 2 камня в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 17. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
- 1.9 7. Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость перевозок между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними. Стоимость перевозок по маршруту складывается из стоимостей перевозок между соседними станциями. Перевозки между населёнными пунктами А, В, С, В, Е осуществляют три компании, представившие стоимость своих услуг в табличной форме. Какая компания обеспечивает минимальную стоимость перевозок из А в В?
- 1.10 8. Соревнования по плаванию были в самом разгаре, когда стало ясно, что первые четыре места займут мальчики из пятёрки лидеров. Их имена: Валерий, Николай, Михаил, Игорь, Эдуард, фамилии: Симаков, Чигрин, Зимин, Копылов, Блинов (имена и фамилии названы в произвольном порядке). Нашлись знатоки, которые предсказали, что первое место займёт Копылов, второе — Валерий, третье — Чигрин, четвёртое — Эдуард. Но ни один из ребят не занял того места, какое ему предсказывали. На самом деле первое место завоевал Михаил, второе — Симаков, третье — Николай, четвёртое — Блинов, а Чигрин не попал в четвёрку сильнейших. Назовите имя и фамилию каждого из лидеров.
- 1.11 9. В Норильске, Москве, Ростове и Пятигорске живут четыре супружеские пары (в каждом городе — одна пара). Имена этих супругов: Антон, Борис, Давид, Григорий, Ольга, Мария, Светлана, Екатерина. Антон живёт в Норильске, Борис и Ольга — супруги, Григорий и Светлана не живут в одном городе, Мария живёт в Москве, Светлана — в Ростове. В каком городе живёт каждая из супружеских пар?
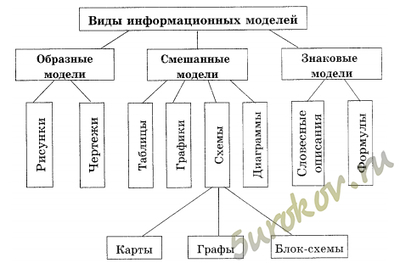
- 1.12 10. Постройте граф, отражающий разновидности информационных моделей
Глава 1. МОДЕЛИРОВАНИЕ И ФОРМАЛИЗАЦИЯ
§1.4.Табличные информационные модели ГДЗ, Информатика 9 класс Босова ответы на «Вопросы и задания»
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.
2. Какие преимущества обеспечивают табличные информационные модели по сравнению со словесными описаниями? Приведите пример
Преимуществом табличной информационной модели является компактность и легкообозримость.
3. Примеры табличный информационных моделей:
а) на уроках в школе: таблица умножения, таблица Менделеева, расписание уроков, школьный дневник и журнал
б) в повседневной жизни: календарь, расписание движения автобусов
4. К какому типу относится таблица «Табель успеваемости», расположенная в конце вашего дневника?
Таблица «Табель успеваемости» является таблицей «объект-свойство».
5. Узнайте, в каких случаях в ячейку таблицы ставится знак «х». Почему мы использовали этот знак в таблице (пример 2)?
Этот знак(х) мы ставим тогда, когда значение в этой ячейке невозможно и оно пустое.
6. Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 1 камень, а во второй — 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 2 камня в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 17. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
Рассмотрим все варианты ходов первого игрока. Различных вариантов у него оказывается 3, так как 1 · 3 = 3 и 1 + 2 = 3. Поэтому во 2-м столбце заполним только 3 ячейки.
Пусть после хода 1-го игрока в кучах оказалось 3 и 2 камня. Рассмотрим все варианты ходов 2-го игрока. Из таблицы видно, что только один из его ходов не позволит выиграть первому игроку своим вторым ходом. Это ситуация, когда в кучах окажется по 3 и 4 камня. Вернемся к ее рассмотрению чуть позже.
Первый игрок не должен сделать ход, приводящий к ситуации, когда в кучах окажется 1 и 6 камней, так как в этом случае второй игрок получает возможность выиграть, утроив число камней во второй куче.
Если после хода 1-го игрока в кучах оказалось 1 и 4 камня, то второй игрок не сможет добиться выигрыша своим первым ходом. Но два его хода, в результате которых в кучах окажется по 3 и 4 камня, не позволят выиграть первому игроку своим вторым ходом. Рассмотрим эту ситуацию подробно.
Представим все варианты второго хода первого игрока, если в результате хода второго игрока в кучах оказалось 3 и 4 камня. Ни один из ходов первого игрока не может привести к победе, но такая возможность появляется у второго игрока.
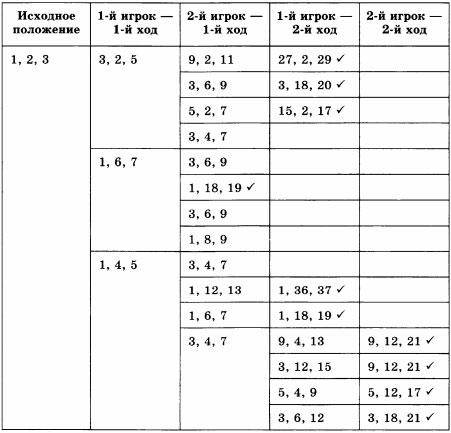
Ответ:
При безошибочной игре соперников побеждает второй игрок. У него есть шанс выиграть первым ходом. Иначе его первый ход должен быть таким, чтобы в кучах оказалось 3 и 4 камня.
7. Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость перевозок между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними. Стоимость перевозок по маршруту складывается из стоимостей перевозок между соседними станциями. Перевозки между населёнными пунктами А, В, С, В, Е осуществляют три компании, представившие стоимость своих услуг в табличной форме. Какая компания обеспечивает минимальную стоимость перевозок из А в В?
Для большей наглядности перейдем от таблиц к графам:
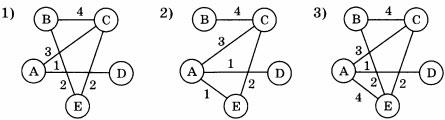
Минимальная стоимость у 1 компании
ACB = 3 + 4 = 7
Минимальная стоимость у 2 компании
ACB = 3 + 4 = 7
AECB = 1 + 2 + 4 = 7
Минимальная стоимость у 3 компании
ACB = 3 + 4 = 7
AECB = 4 + 2 + 4 = 10
AEB = 4 + 2 = 6
Ответ:
Третья компания.
8. Соревнования по плаванию были в самом разгаре, когда стало ясно, что первые четыре места займут мальчики из пятёрки лидеров. Их имена: Валерий, Николай, Михаил, Игорь, Эдуард, фамилии: Симаков, Чигрин, Зимин, Копылов, Блинов (имена и фамилии названы в произвольном порядке). Нашлись знатоки, которые предсказали, что первое место займёт Копылов, второе — Валерий, третье — Чигрин, четвёртое — Эдуард. Но ни один из ребят не занял того места, какое ему предсказывали. На самом деле первое место завоевал Михаил, второе — Симаков, третье — Николай, четвёртое — Блинов, а Чигрин не попал в четвёрку сильнейших. Назовите имя и фамилию каждого из лидеров.
Прогноз
1. Копылов
2. Валерий
3. Чигрин
4. Эдуард
5. —
Результат
1. Михаил
2. Симаков
3. Николай
4. Блинов
5. Чигрин
Исходя из результата фамилия Михаила не Симаков, не Блинов и не Чигрин. Исходя из прогноза так же не Копылов. Значит, Михаил Зимин — 1 место.
Валерий не Симаков и не Чигрин. Значит, Валерий Блинов — 4 место.
Эдуард не Блинов, не Чигрин, Эдуард Симаков — 2 место.
Остались фамилии Чигрин, Копылов и имена Николай, Игорь. Чигрин так и остался в прогнозе в результате под одинаковым обозначением (фамилией), значит, имя Николай принадлежит Николаю Копылову — 3 место.
Чигрин Игорь — 5 место.
Ответ:
Михаил Зимин,
Эдуард Симаков,
Николай Копылов,
Валерий Блинов,
Игорь Чигрин.
9. В Норильске, Москве, Ростове и Пятигорске живут четыре супружеские пары (в каждом городе — одна пара). Имена этих супругов: Антон, Борис, Давид, Григорий, Ольга, Мария, Светлана, Екатерина. Антон живёт в Норильске, Борис и Ольга — супруги, Григорий и Светлана не живут в одном городе, Мария живёт в Москве, Светлана — в Ростове. В каком городе живёт каждая из супружеских пар?
Антон живет в Норильске, Светлана — в Ростове, Мария — в Москве.
Значит Борис и Ольга живут в Пятигорске.
Светлана и Георгий не живут в одном городе и это значит, что Георгий живет с Марией в Москве.
Остались Давид и Екатерина. Екатерина живет с Антоном в Норильске, а Давид живет со Светланой в Ростове.
Ответ:
Антон и Екатерина проживают в Норильске,
Григорий и Мария — в Москве,
Давид и Светлана — в Ростове,
Борис и Ольга — в Пятигорске.
10. Постройте граф, отражающий разновидности информационных моделей
Решение заданий из учебника Информатика 9 класс Босова, параграф 1.4.Табличные информационные модели.
На этой странице размещен вариант решения заданий с страниц учебника по информатике за 9 класс авторов Босова. Здесь вы сможете списать решение домашнего задания или просто посмотреть ответы. ГДЗ
Литература: Учебник по Информатике, 9 класс. Автор: Босова Л.Л., Босова А.Ю. Издательство: Бином. Год: 2016, 2017
Did you find apk for android? You can find new Free Android Games and apps.