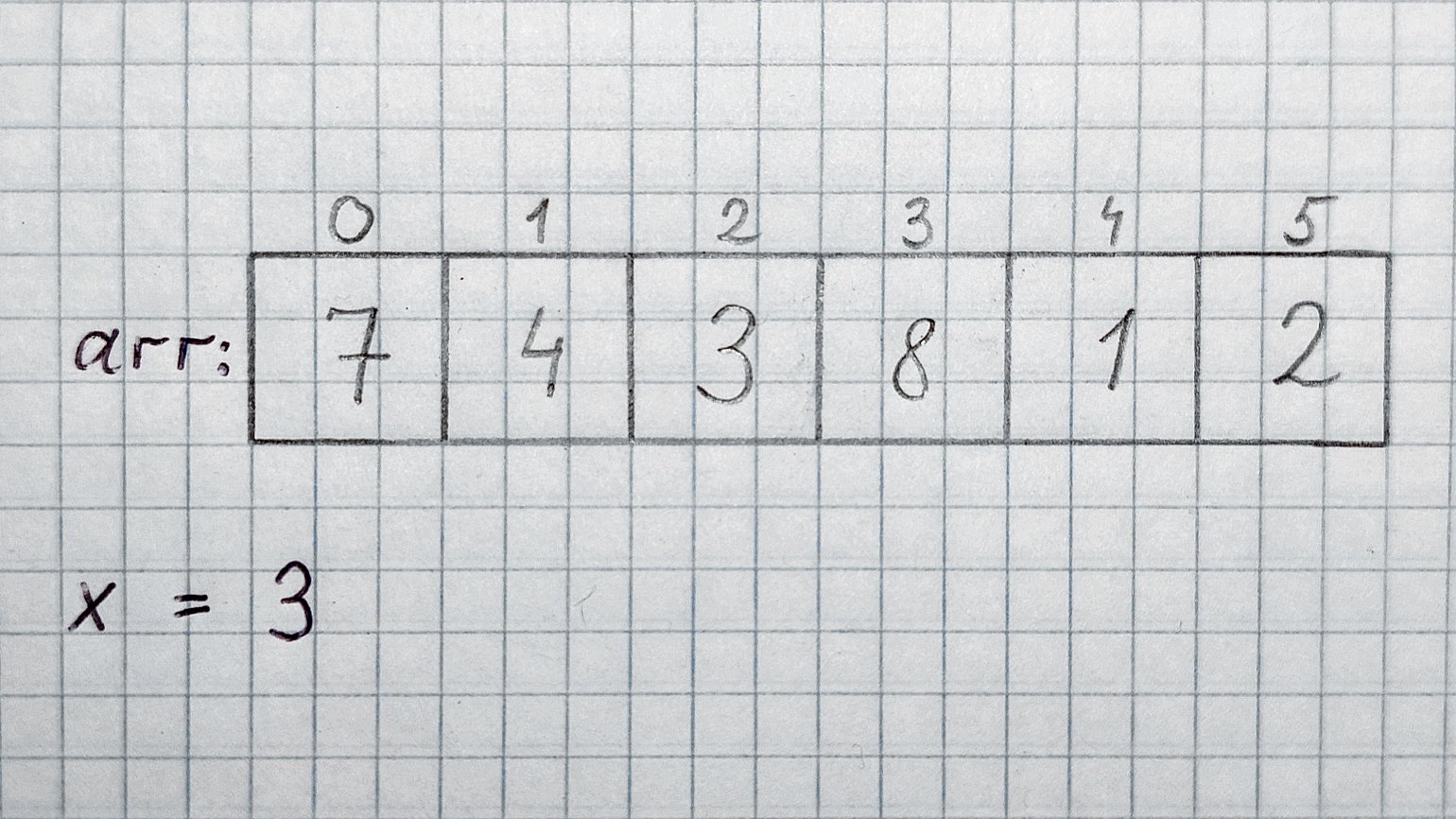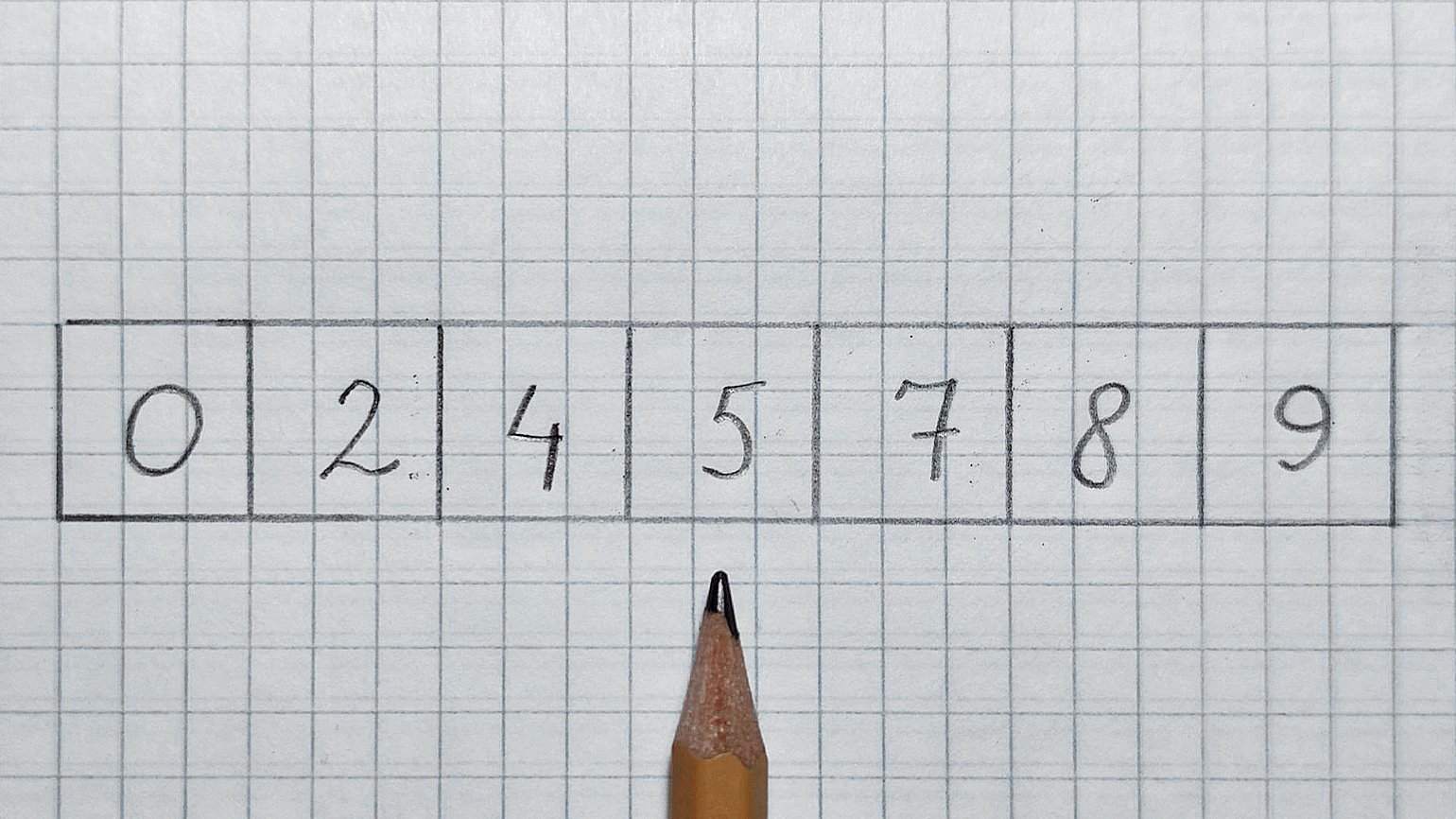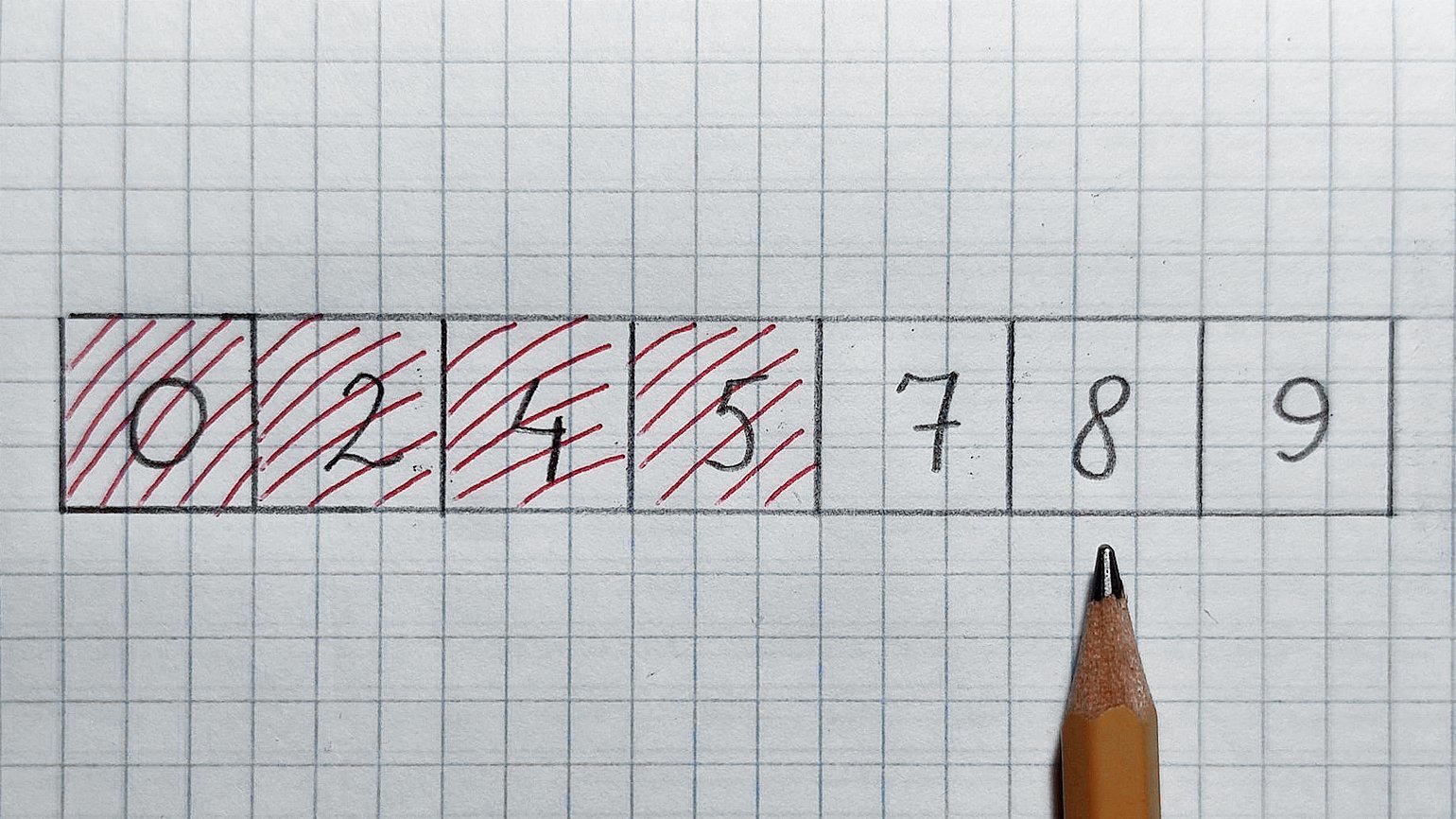§22. Сложность алгоритмов.
Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)
Как сравнивать алгоритмы?
Ключевые слова:
• временная сложность • пространственная сложность • время работы алгоритма • асимптотическая сложность • линейная сложность • квадратичная сложность
Большинство задач могут быть решены по-разному, с помощью разных алгоритмов. Поэтому возникает вопрос: как выбрать лучший? И ещё один важный вопрос — способен ли современный компьютер за приемлемое время найти решение задачи? Например, в игре в шахматы возможно лишь конечное количество позиций и, следовательно, только конечное количество различных партий. Значит, теоретически можно перебрать все возможные партии и выяснить, кто побеждает при правильной игре — белые или чёрные. Однако количество вариантов настолько велико, что современные компьютеры не могут выполнить такой перебор за приемлемое время.
Что мы хотим от алгоритма? Во-первых, чтобы он работал как можно быстрее. Во-вторых, чтобы объём необходимой памяти был как можно меньше. В-третьих, чтобы он был как можно более прост и понятен, что позволяет легче отлаживать программу. К сожалению, эти требования противоречивы, и в серьёзных задачах редко удаётся найти алгоритм, который был бы лучше остальных по всем показателям.
Часто говорят о временной сложности алгоритма (быстродействии) и пространственной сложности, которая определяется объёмом необходимой памяти.
Временем работы алгоритма называется количество элементарных операций T, выполненных исполнителем.
Такой подход позволяет оценивать именно качество алгоритма, а не свойства исполнителя (например, быстродействие компьютера, на котором выполняется алгоритм). При этом мы считаем, что время выполнения всех элементарных операций одинаково.
Как правило, величина Т будет существенно зависеть от объёма исходных данных: поиск в списке из 10 элементов завершится гораздо быстрее, чем в списке из 10000 элементов. Поэтому сложность алгоритма обычно связывают с размером входных данных N и определяют как функцию T(N). Например, для алгоритмов обработки массивов в качестве размера N используют длину массива. Функция T(N) называется временной сложностью алгоритма.
Временная сложность агоритма определяется функцией T(N) = 2N3. Во сколько раз увеличится время работы алгоритма, если размер данных N увеличится в 10 раз?
Пространственная сложность — это зависимость объёма занимаемой памяти от размера данных N. Для ускорения работы некоторых алгоритмов нужно использовать дополнительную память, которая может быть намного больше, чем память для хранения исходных данных.
Для быстрой сортировки массива из N элементов с помощью алгоритма Семёна требуется N вспомогательных массивов, каждый из которых содержит N элементов. Как изменится объём нужной дополнительной памяти, если N увеличится в 10 раз?
Поскольку память постоянно дешевеет, а быстродействие компьютеров растёт медленно, более важна временная сложность алгоритмов. Пространственную сложность мы дальше рассматривать не будем.
Примеры вычисления сложности
Рассмотрим алгоритмы выполнения различных операций с массивом А длины N, который может быть объявлен в программе так:
целтаб А[1:N] var A: array[1..N] of integer;
Пример 1. Вычислить сумму значений первых трёх элементов массива (при N ? 3).
Решение этой задачи содержит всего один оператор:
Sum:=А[1]+А[2]+А[3];
Этот алгоритм включает две операции сложения и одну операцию записи значения в память, поэтому его сложность T(N) = 3 не зависит от размера массива вообще.
Вычислите количество операций (считая сравнения и присваивание значений переменным) при выполнении фрагмента программы:

Пример 2. Вычислить сумму значений всех элементов массива.
В этой задаче уже не обойтись без цикла:

Здесь выполняется N операций сложения и N + 1 операция записи в память, поэтому его сложность T(N) = 2N + 1 возрастает линейно с увеличением длины массива.
Вычислите количество операций при выполнении фрагмента программы:

Пример 3. Отсортировать все элементы массива по возрастанию методом выбора. Напомним, что метод выбора предполагает поиск на каждом шаге минимального из оставшихся неупорядоченных значений (здесь i, j, nMin и с — целочисленные переменные):

Подсчитаем отдельно количество сравнений и количество перестановок. Количество сравнений элементов массива не зависит от данных и определяется числом шагов внутреннего цикла:

Здесь использована формула для суммы первых N — 1 членов арифметической прогрессии.
На каждом шаге внешнего цикла происходит перестановка двух элементов, общее количество перестановок равно Тn( N) = N -1, т. е. сложность по перестановкам — линейная.
Определите количество операций при вычислении суммы значений элементов квадратной матрицы А размером N х N (здесь i, j и Sum — целочисленные переменные):

По результатам этих примеров можно сделать выводы:
• простой цикл, в котором количество шагов пропорционально N, — это алгоритм линейной сложности;
• вложенный цикл, в котором количество шагов внешнего и внутреннего цикла пропорционально N, — это алгоритм квадратичной сложности.
Что такое асимптотическая сложность?
Допустим, что нужно сделать выбор между несколькими алгоритмами, которые имеют разную сложность. Какой из них лучше (работает быстрее)? Оказывается, для этого необходимо знать размер массива данных, которые нужно обрабатывать. Сравним, например, три алгоритма, сложность которых
T1(N) = 10000 • N, T2(N) = 100 • N2 и T3(N) = N3.
Построим эти зависимости на графике (рис. 4.5). При N ? 100 получаем Т3(N) < T2(N) < T1N), при N = 100 количество операций для всех трёх алгоритмов совпадёт, а при больших N имеем Т3(N) > T2(N) > T1N).

Рис. 4.5
Обычно в теоретической информатике при сравнении алгоритмов используется их асимптотическая сложность, т. е. скорость роста количества операций при больших значениях N.
Запись 0(N) (читается «О большое от N») обозначает линейную сложность алгоритма. Это значит, что, начиная с некоторого значения N = N0, количество операций будет меньше, чем с•N, где с — некоторая постоянная:
T(N)?c•N для N?N0.
При увеличении размера данных в 10 раз объём вычислений алгоритма с линейной сложностью увеличивается тоже примерно в 10 раз.
Пусть, например, T(N) = 2N — 1, как в алгоритме поиска суммы значений элементов массива. Очевидно, что при этом T(N) ? 2N для всех N ? 1, поэтому алгоритм имеет линейную сложность.
Определите любые подходящие значения с и N0, такие что T(N) ? с•N для N ? N0, для алгоритмов с линейной асимптотической сложностью:
a) T(N) = 12N — 8;
б) T(N) = 7N + 5.
Многие известные алгоритм имеют квадратичную сложность 0(N2). Это значит, что сложность алгоритма при больших N меньше, чем с•N2:
T(N)?c•N2 для N?N0.
Если размер данных увеличивается в 10 раз, то количество операций (и время выполнения такого алгоритма) увеличивается примерно в 100 раз. Пример алгоритма с квадратичной сложностью — сортировка методом выбора, для которой число сравнений

Определите любые подходящие значения с и N0, такие что T(N) ? с•N2 для N ? N0, для алгоритмов с квадратичной асимптотической сложностью:
a) T(N) = 5N2 — 3N — 2;
б) T(N) = 7N2 — 3N — 5.
Алгоритм имеет асимптотическую сложность 0(f(N)), если найдется такая постоянная с, что, начиная с некоторого N = N0, выполняется условие T(N)?c•f(N).
Это значит, что график функции с•f(N) проходит выше, чем график функции T(N), по крайней мере, при N?N0 (рис. 4.6).

Рис. 4.6
Если количество операций не зависит от размера данных, то говорят, что асимптотическая сложность алгоритма 0(1), т. е. количество операций меньше некоторой постоянной при любых N.
Существует также немало алгоритмов с кубической сложностью 0(N3). При больших значениях N алгоритм с кубической сложностью требует большего количества вычислений, чем алгоритм со сложностью 0(N2), а тот, в свою очередь, работает дольше, чем алгоритм с линейной сложностью. Однако при небольших значениях N всё может быть наоборот, это зависит от постоянной с для каждого из алгоритмов.
Известны и алгоритмы, для которых количество операций растёт быстрее, чем любой многочлен, например как 0(2N) или 0(N!), где N! обозначает факториал числа N — произведение всех натуральных чисел от 1 до N : N! = 1 • 2 • 3 •… • N. Такие алгоритмы встречаются чаще всего в задачах поиска оптимального (наилучшего) варианта, которые решаются только методом полного перебора. Самая известная задача такого типа — это задача коммивояжёра (бродячего торговца), который должен посетить по одному разу каждый из указанных городов и вернуться в начальную точку. Для него нужно выбрать маршрут, при котором стоимость поездки (или общая длина пути) будет минимальной.
В таблице 4.1 показано примерное время работы алгоритмов, имеющих разную временную сложность, при N = 100 на компьютере с быстродействием 1 миллиард операций в секунду.
Таблица 4.1
| T(N) | Время выполнения |
| N | 100 нc |
| N2 | 10 мс |
| N3 | 0,001 с |
| 2N | 1013 лет |
Юный программист Григорий поспорил с учителем, что сможет к завтрашнему уроку с помощью компьютера решить сложную задачу перебора вариантов. Дома он определил временную сложность алгоритма: T(N) = 2N. Для какого наибольшего значения N сможет Григорий решить задачу за сутки, если его компьютер выполняет 1 миллиард операций в секунду?
Выводы
• Временем работы алгоритма называется количество элементарных операций Т, выполненных исполнителем.
• Временная сложность алгоритма обычно зависит от объёма исходных данных N, например от размера массива.
• Пространственная сложность — это объём памяти, необходимой для работы алгоритма.
• Простой цикл, в котором количество шагов пропорционально N, — это алгоритм линейной сложности.
• Вложенный цикл, в котором количество шагов внешнего и внутреннего цикла пропорционально N, — это алгоритм квадратичной сложности.
• Алгоритм имеет асимптотическую сложность 0(f(N)), если найдётся такая постоянная с, что, начиная с некоторого N = N0, выполняется условие T(N) ? с • f(N).
• Линейная сложность означает, что при увеличении размера массива в К раз количество операций увеличивается примерно в К раз.
• Квадратичная сложность означает, что при увеличении размера массива в К раз количество операций увеличивается примерно в К2 раз.
Нарисуйте в тетради интеллект-карту этого параграфа.
Вопросы и задания
1. Какие критерии используются для оценки алгоритмов?
2. Почему скорость работы алгоритма оценивается не временем выполнения, а количеством элементарных операций?
3. Как учитывается размер данных при оценке быстродействия алгоритма?
4. В каких случаях алгоритм, имеющий асимптотическую сложность 0(N2), может работать быстрее, чем алгоритм с асимптотической сложностью 0(N)?
5. Выполните по указанию учителя задания в рабочей тетради.
Подготовьте сообщение
«Задача коммивояжёра»
Оглавление
§21. Матрицы (двумерные массивы).
§22. Сложность алгоритмов.
§23. Как разрабатывают программы?
|
1. Какие критерии используются для оценки алгоритмов? Для оценки алгоритмов используются следующие критерии: 2. Почему скорость работы алгоритма оценивается не временем выполнения, а количеством элементарных операций? Скорость работы алгоритма оценивается не временем выполнения, а количеством элементарных операций, потому что время выполнения может зависеть от многих факторов, таких как процессор, операционная система, объем данных и другие факторы, которые могут повлиять на скорость выполнения. Количество элементарных операций является более объективной метрикой, так как оно зависит только от алгоритма. 3. Как учитывается размер данных при оценке быстродействия алгоритма? Размер данных учитывается при оценке быстродействия алгоритма, потому что скорость выполнения алгоритма может зависеть от объема входных данных. Чем больше данных необходимо обработать, тем больше времени может потребоваться на выполнение алгоритма. 4. В каких случаях алгоритм, имеющий асимптотическую сложность O(N2), может работать быстрее, чем алгоритм с асимптотической сложностью O(N)? Алгоритм, имеющий асимптотическую сложность O(N2), может работать быстрее, чем алгоритм с асимптотической сложностью O(N), в том случае, если у алгоритма с более высокой сложностью меньше константных затрат на выполнение каждой операции, или если у алгоритма с более низкой сложностью больше константных затрат на выполнение каждой операции. В реальных приложениях часто используются оптимизации, которые могут ускорить алгоритмы с более высокой сложностью, такие как кэширование и предварительная обработка данных. Однако в целом алгоритмы с более низкой сложностью выполняются быстрее при больших объемах данных. |
Вы просматриваете решебник по информатике 9 класс учебник Поляков, Еремин § 25. Сложность алгоритмов
Сообщить о неточной информации или отсутствии ответов
| Проверочный код, год рождения Д.И.Менделеева: |
Специальная нотация «О-большое» описывает скорость работы алгоритма. Зачем вам это? Время от времени вам предется использовать чужие алгоритмы. Поэтому неплохо было бы понимать, насколько быстро или медленно они работают. В этой статье я объясню, что представляет собой «О-большое», и приведу список самых распространенных вариантов времени выполнения для некоторых алгоритмов.
Время выполнения алгоритмов растет с разной скоростью
«О-большое» описывает, насколько быстро работает алгоритм. предположим, имеется список размером n. Простой поиск должен проверить каждый элемент, поэтому ему придется выполнить n операций. Время выполнения «О-большое» имеет вид О(n). постойте, но где же секунды? А их здесь нет — «О-большое» не сообщает скорость в секундах, а позволяет сравнить количество операций. Оно указывает, насколько быстро возрастает время выполнения алгоритма.:
Такая запись сообщает количество операций, которые придется выполнить алгоритму. Поэтому, она называется «О-большое», потому что перед количеством операций становится символ «О».
«О-большое» определяет время выполнения в худшем случае
Предположим, вы используете простой поиск для поиска фамилий в телефонной книге. Вы знаете, что простой поиск выполняется за время O(n), то есть в худшем случае вам придется просмотреть каждую без исключения запись в телефонной книге. Но представьте, что искомая фамилия начинается на букву «А» и этот человек стоит на самом первом месте в вашей книге. В общем, вам не пришлось просматривать все записи — вы нашли нужную фамилию с первой попытки. Отработал ли алгоритм за время O(n)? А может, он занял время O(1), потому что результат был получен с первой попытки?
Простой поиск все равно выполняется за время O(n). просто в данном случае вы нашли нужное значение моментально; это лучший возможный случай. Однако «О-большое» описывает худший возможный случай. Фактически вы утверждаете, что в худшем случае придется просмотреть каждую запись в телефонной книге по одному разу. Это и есть время O(n). И это дает определенные гарантии — вы знаете, что простой поиск никогда не будет работать медленнее O(n).
Типичные примеры «О-большого»
Ниже перечислены пять разновидностей «О-большого», которые будут встречаться вам особенно часто, в порядке убывания скорости выполнения.
- O(log n), или логарифмическое время. Пример: бинарный поиск.
- O(n), или линейное время. Пример: простой поиск.
- O(n * log n). Пример: эффективные алгоритмы сортировки (быстрая сортировка)
- O(n^2). Пример: медленные алгоритмы сортировки (сортировка выбором)
- O(n!). Пример: очень медленные алгоритмы.
Основные результаты:
- Скорость алгоритмов изменяерся не в секундах, а в теме роста количества операций.
- По сути формула описывает, насколько быстро возрастает время выполнения алгоритма с увеличением размера входных данных.
- Время выполнения алгоритмов выражается как «О-большое».
- Время выполнения O(log n) быстрее O(n), а с увеличением размера списка, в котором ищется значение, оно становится намного быстрее.
Наглядное представление «О-большое»
Допустим, вы должны построить сетку из 16 квадратов:
Алгоритм 1:
Как вариант можно нарисовать 16 квадратов, по одному за раз. Напоминаю: «О-большое» подсчитывает количество операций. В анном примере рисование квадрата считается одной операцией. Нужно нарисовать 16 квадратов. Сколько операций по рисованию одного квадрата придется выполнить?
Чтобы нарисовать 16 квадратов, потребуется ё6 шагов. Как выглядит время выполнения этого алгоритма?
Алгоритм 2:
А теперь попробуем иначе. Сложите лист пополам.
На этот раз операцией считается сложение листа. Получается, что одна операция создает сразу два прямоугольника!
Сложите бумагу еще раз, а потом еще и еще.
Разверните листок после четырех сложений — получилось замечательная сетка! Каждое сложение удваивает количество прямоугольников. За 4 операции вы создали 16 прямоугольников!
При каждом складывании количество прямоугольников увеличивается вдвое, так что 16 прямоугольников строятся за 4 шага. Как записать время выполнения этого алгоритма? Напишите время выполнения обоих алгоритмов.
Ответы: алгоритм 1 выполняется за время O(n), а алгоритм 2 — за время O(log n).
Упражнения на понимание «О-большое»
Приведите время выполнения «О-большое» для каждого из следующих сценариев.
- Известа фамилия, нужно найти номер в телефонной книге.
- Известен номер, нужно найти фамилию в телефонной книге. (Подсказка: вам придется провести поиск по всей книге!)
- Нужно прочитать телефоны всех людей в телефонной книге.
Ответы:
- O(log n)
- O(n)
- O(n)
Чтобы не пропускать новые выпуски подписывайтесь на канал @world_hello_ru
Оценка
времени работы алгоритма
Алгоритм
– формальная вычислительная процедура,
т.е. последовательность шагов, которая
получает результат по входным данным.
Программа
– реализация алгоритма.
При
анализе алгоритма нас в первую очередь
волнует его трудоемкость, т.е. время
выполнения алгоритма на компьютере.
Очевидно, что этот показатель напрямую
зависит от конкретного компьютера,
поэтому чтобы сделать наши вычисления
о трудоемкости алгоритмов более
универсальными, будет считать, что все
вычисления проводятся на некой абстрактной
машине. RAM-машина
– абстрактный исполнитель, используемый
для анализа алгоритмов, способный
выполнять некие элементарные действия.
Мы
принимаем, что каждое такое действие
выполняется за единицу времени, поэтому
время работы алгоритма в нашем понимании
– это количество выполненных действий.
Размер
или количество входных данных – есть
размерность
данных.
Определим
сложность алгоритма как функцию Т от
размерности данных n.
Эта функция ставит каждому n
в соответствие наибольшее время T(n)
работы алгоритма при входных данных
размерности n.
Таким
образом, анализ времени работы алгоритма
сводится к вопросу: как быстро растет
функция T
при бесконечно растущем значении n.
Иными словами, нас интересует
асимптотическая сложность алгоритма.
Несмотря
на то, что функция сложности может быть
иногда определена очень точно, в
большинстве случаев это не требуется,
т.к. при входных данных достаточно
большой размерности постоянные множители
и слагаемые низших порядков оказывают
незначительный вклад в итоговую оценку
сложности. Например, если количество
действий в алгоритме оценивается как
многочлен, то можно пренебречь всеми
слагаемыми и константами кроме слагаемого
старшей степени.
Нотации
О, Омега и Тетта
Функция
f(n)
= O(g(n))
существуют C,
N
такие, что для любых n
> N:
f(n)
< C
* g(n).
Или предел отношения функций f(n)/g(n)
при n
стремящемся к бесконечности <= C.
В
этом случае, g(n)
– асимптотическая оценка СВЕРХУ для
функции f(n).
Т.е. алгоритм заканчивает свою работу
при любых входных данных не более, чем
за C
* g(n)
элементарных операций. O(1)
– такой алгоритм не зависит от размера
входных данных и всегда выполняется
константное количество времени, O(n)
– линейный алгоритм, O(N^C)
– полиномиальный.
Для
оценки СНИЗУ
используется обозначение ОМЕГА БОЛЬШОЕ.
Функция f(n)
= Omega(g(n))
существуют C,
N
такие, что для любых n
> N:
f(n)
>= C
* g(n).
Чтобы
точно указать порядок роста функции,
не давая точных значений констант,
используется обозначение Тетта Большое.
F(n)
= Theta(g(n))
существуют N,
C1,
C2
такие, что для любых n
> N:
C1
* g(n)
<= f(n)
<= C2
* g(n).
Такая запись включает в себя сразу 2
оценки – сверху и снизу, т.е. начиная с
некоторого N
скорость роста функции g(n)
полностью соответствует росту функции
f(n).
Оценка
времени работы алгоритмов
Время
работы алгоритма может быть оценено в
худшем случае (сверху), в лучшем случае
(снизу) и в среднем случае. Однако очень
часто время работы в худшем и среднем
случае мало отличается.
Среднее
время работы – усредненное время работы
алгоритма по всем входным данным
размерности n.
Т.е. в среднем случае мы рассматриваем
различные входные данные как равновероятные.
Соседние файлы в папке Bilety_OI_2
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
#статьи
- 18 янв 2022
-
0
Software Engineer Валерий Жила подробно рассказал, что такое O(n), и показал, как её считать на примере бинарного поиска и других алгоритмов.
Кадр: фильм «Мальчишник в Вегасе»
Онлайн-журнал для тех, кто влюблён в код и информационные технологии. Пишем для айтишников и об айтишниках.
Валерий Жила
об эксперте
Software Engineer, разрабатывает системы управления городской инфраструктурой для мегаполисов. Основная деятельность: backend, database engineering. Ведёт твиттер @ValeriiZhyla и пишет научные работы по DevOps.
Сегодня я расскажу о сложности алгоритмов, или, как её часто называют, Big O Notation. Статья рассчитана на новичков, поэтому постараюсь изложить идеи и концепции просто, не теряя важных деталей.
Алгоритмы описывают с помощью двух характеристик — времени и памяти.
Время — это… время, которое нужно алгоритму для обработки данных. Например, для маленького массива — 10 секунд, а для массива побольше — 100 секунд. Интуитивно понятно, что время выполнения алгоритма зависит от размера массива.
Но есть проблема: секунды, минуты и часы — это не очень показательные единицы измерения. Кроме того, время работы алгоритма зависит от железа, на котором он выполняется, и других внешних факторов. Поэтому время считают не в секундах и часах, а в количестве операций, которые алгоритм совершит. Это надёжная и, главное, независимая от железа метрика.
Когда говорят о Time Complexity или просто Time, то речь идёт именно о количестве операций. Для простоты расчётов разница в скорости между операциями обычно опускается. Поэтому, несмотря на то, что деление чисел с плавающей точкой требует от процессора больше действий, чем сложение целых чисел, обе операции в теории алгоритмов считаются равными по сложности.
Запомните: в О-нотации на операции с одной или двумя переменными вроде i++, a * b, a / 1024, max(a,b) уходит всего одна единица времени.
Память, или место, — это объём оперативной памяти, который потребуется алгоритму для работы. Одна переменная — это одна ячейка памяти, а массив с тысячей ячеек — тысяча ячеек памяти.
В теории алгоритмов все ячейки считаются равноценными. Например, int a на 4 байта и double b на 8 байт имеют один вес. Потребление памяти обычно называется Space Complexity или просто Space, редко — Memory.
Алгоритмы, которые используют исходный массив как рабочее пространство, называют in-place. Они потребляют мало памяти и создают одиночные переменные — без копий исходного массива и промежуточных структур данных. Алгоритмы, требующие дополнительной памяти, называют out-of-place. Прежде чем использовать алгоритм, надо понять, хватит ли на него памяти, и если нет — поискать менее прожорливые альтернативы.
Статья написана на основе треда Валерия в его аккаунте в Twitter. Автор благодарит @usehex за помощь в создании материала.
Давайте вспомним 8-й класс и разберёмся: что значит запись O(n) с математической точки зрения. При расчёте Big O Notation используют два правила:
Константы откидываются. Нас интересует только часть формулы, которая зависит от размера входных данных. Проще говоря, это само число n, его степени, логарифмы, факториалы и экспоненты, где число находится в степени n.
Примеры:
O(3n) = O(n)
O(10000 n^2) = O(n^2)
O(2n * log n) = O(n * log n)
Если в O есть сумма, нас интересует самое быстрорастущее слагаемое. Это называется асимптотической оценкой сложности.
Примеры:
O(n^2 + n) = O(n^2)
O(n^3 + 100n * log n) = O(n^3)
O(n! + 999) = O(n!)
O(1,1^n + n^100) = O(1,1^n)
У каждого алгоритма есть худший, средний и лучший сценарии работы — в зависимости от того, насколько удачно выбраны входные данные. Часто их называют случаями.
Худший случай (worst case) — это когда входные данные требуют максимальных затрат времени и памяти.
Например, если мы хотим отсортировать массив по возрастанию (Ascending Order, коротко ASC), то для простых алгоритмов сортировки худшим случаем будет массив, отсортированный по убыванию (Descending Order, коротко DESC).
Для алгоритма поиска элемента в неотсортированном массиве worst case — это когда искомый элемент находится в конце массива или если элемента нет вообще.
Лучший случай (best case) — полная противоположность worst case, самые удачные входные данные. Правильно отсортированный массив, с которым алгоритму сортировки вообще ничего делать не нужно. В случае поиска — когда алгоритм находит нужный элемент с первого раза.
Средний случай (average case) — самый хитрый из тройки. Интуитивно понятно, что он сидит между best case и worst case, но далеко не всегда понятно, где именно. Часто он совпадает с worst case и всегда хуже best case, если best case не совпадает с worst case. Да, иногда они совпадают.
Как определяют средний случай? Считают статистически усреднённый результат: берут алгоритм, прокручивают его с разными данными, составляют сводку результатов и смотрят, вокруг какой функции распределились результаты. В общем, расчёт average case — дело сложное. А мы приступаем к конкретным алгоритмам.
Начнём с самого простого алгоритма — линейного поиска, он же linear search. Дальнейшее объяснение подразумевает, что вы знаете, что такое числа и как устроены массивы. Напомню, это всего лишь набор проиндексированных ячеек.
Допустим, у нас есть массив целых чисел arr, содержащий n элементов. Вообще, количество элементов, размер строк, массивов, списков и графов в алгоритмах всегда обозначают буквой n или N. Ещё дано целое число x. Для удобства обусловимся, что arr точно содержит x.
Задача: найти, на каком месте в массиве arr находится элемент 3, и вернуть его индекс.
Меткий человеческий глаз сразу видит, что искомый элемент содержится в ячейке с индексом 2, то есть в arr[2]. А менее зоркий компьютер будет перебирать ячейки друг за другом: arr[0], arr[1]… и так далее, пока не встретит тройку или конец массива, если тройки в нём нет.
Теперь разберём случаи:
Worst case. Больше всего шагов потребуется, если искомое число стоит в конце массива. В этом случае придётся перебрать все n ячеек, прочитать их содержимое и сравнить с искомым числом. Получается, worst case равен O(n). В нашем массиве худшему случаю соответствует x = 2.
Best case. Если бы искомое число стояло в самом начале массива, то мы бы получили ответ уже в первой ячейке. Best case линейного поиска — O(1). Именно так обозначается константное время в Big O Notation. В нашем массиве best case наблюдается при x = 7.
Average case. В среднем случае результаты будут равномерно распределены по массиву. Средний элемент можно рассчитать по формуле (n + 1) / 2, но так как мы отбрасываем константы, то получаем просто n. Значит, average case равен O(n). Хотя иногда в среднем случае константы оставляют, потому что запись O(n / 2) даёт чуть больше информации.
Хорошо, мы уже три минуты обсуждаем linear search, но до сих пор не видели кода. Потерпите, скоро всё будет. Но сперва познакомимся с очень полезным инструментом — псевдокодом.
Разработчики пишут на разных языках программирования. Одни похожи друг на друга, а другие — сильно различаются. Часто мы точно знаем, какую операцию хотим выполнить, но не уверены в том, как она выглядит в конкретном языке.
Возьмём хотя бы получение длины массива. По историческим причинам практически во всех языках эта операция называется по-разному: .length, length(), len(), size(), .size — попробуй угадай! Как же объяснить свой код коллегам, которые пишут на другом языке? Написать программу на псевдокоде.
Псевдокод — достаточно формальный, но не слишком требовательный к мелочам инструмент для изложения мыслей, не связанный с конкретным языком программирования.
Прелесть псевдокода в том, что конкретных правил для его написания нет. Я, например, предпочитаю использовать смесь синтаксиса Python и C: обозначаю вложенность с помощью отступов и называю методы в стиле Python.
А вот и пример псевдокода для нашей задачи, со всеми допущениями и упрощениями. Метод должен возвращать -1, если arr пуст или не содержит x:
int linear_search(int[] arr, int x): if arr is empty: return -1 for i in 0..n: if (arr[i] == x): return i return -1 //x was not found
В псевдокоде часто используют -1 в качестве invalid index, а если алгоритм возвращает объекты — null, nil (то же самое, что и null) или специальный символ «ничего», похожий на перевёрнутую букву «т». Также встречаются конструкции для исключений, вроде throw error («Very Bad»).
Уметь писать псевдокод полезно. Например, с его помощью можно решать задачи на доске на технических собеседованиях. Я пишу код на бумаге и доске почти так же, как в компьютере, но ещё явно выделяю отступы — иначе строчки кода разъезжаются куда глаза глядят:
Следующая остановка — binary search, он же бинарный, или двоичный, поиск.
В чём отличие бинарного поиска от уже знакомого линейного? Чтобы его применить, массив arr должен быть отсортирован. В нашем случае — по возрастанию.
Часто binary search объясняют на примере с телефонным справочником. Возможно, многие читатели никогда не видели такую приблуду — это большая книга со списками телефонных номеров, отсортированных по фамилиям и именам жителей. Для простоты забудем об именах.
Итак, есть огромный справочник на тысячу страниц с десятками тысяч пар «фамилия — номер», отсортированных по фамилиям. Допустим, мы хотим найти номер человека по фамилии Жила. Как бы мы действовали в случае с линейным поиском? Открыли бы книгу и начали её перебирать, строчку за строчкой, страницу за страницей: Астафьев… Безье… Варнава… Ги… До товарища Жилы он дошёл бы за пару часов, а вот господин Янтарный заставил бы алгоритм попотеть ещё дольше.
Бинарный поиск мудрее и хитрее. Он открывает книгу ровно посередине и смотрит на фамилию, например Мельник — буква «М». Книга отсортирована по фамилиям, и алгоритм знает, что буква «Ж» идёт перед «М».
Алгоритм «разрывает» книгу пополам и выкидывает часть с буквами, которые идут после «М»: «Н», «О», «П»… «Я». Затем открывает оставшуюся половинку посередине — на этот раз на фамилии Ежов. Уже близко, но Ежов не Жила, а ещё буква «Ж» идёт после буквы «Е». Разрываем книгу пополам, а левую половину с буквами от «А» до «Е» выбрасываем. Алгоритм продолжает рвать книгу пополам до тех пор, пока не останется единственная измятая страничка с заветной фамилией и номером.
Перенесём этот принцип на массивы. У нас есть отсортированный массив arr и число 7, которое нужно найти. Почему поиск называется бинарным? Дело в том, что алгоритм на каждом шаге уменьшает проблему в два раза. Он буквально отрезает на каждом шаге половину arr, в которой гарантированно нет искомого числа.
На каждом шаге мы проверяем только середину. При этом есть три варианта развития событий:
- попадаем в 7 — тогда проблема решена;
- нашли число меньше 7 — отрезаем левую половину и ищем в правой половине;
- нашли число больше 7 — отрезаем правую половину и ищем в левой половине.
Почему это работает? Вспомните про требование к отсортированности массива, и всё встанет на свои места.
Итак, смотрим в середину. Карандаш будет служить нам указателем.
В середине находится число 5, оно меньше 7. Значит, отрезаем левую половину и проверенное число. Смотрим в середину оставшегося массива:
В середине число 8, оно больше 7. Значит, отрезаем правую половинку и проверенное число. Остаётся число 7 — как раз его мы и искали. Поздравляю!
Теперь давайте попробуем записать это в виде красивого псевдокода. Как обычно, назовём середину mid и будем перемещать «окно наблюдения», ограниченное двумя индексами — low (левая граница) и high (правая граница).
int binary_search(int [] arr, int low, int high, int x): if high >= low: mid = round_down((low + high)/2) if arr[mid] == x: // check middle element return mid else if arr[mid] > x: // recursive check left hals return binary_search(arr, low, mid-1, x) else: // recursive check right half return binary_search(arr, mid+1, high, x) else: return -1 // x was not found
Алгоритм организован рекурсивно, то есть вызывает сам себя на строках 7 и 9. Есть итеративный вариант с циклом, без рекурсии, но он кажется мне уродливым. Если не находим искомый элемент, возвращаем -1. В начале работы алгоритма значение low совпадает с началом массива, а high — с его концом. И они бегут навстречу друг другу…
Чтобы запускать алгоритм, не задумываясь о начальных значениях индексов low и high, можно написать такую функцию-обёртку:
int binary_search(int [] arr, int x): if arr_is_empty: return -1 lower_bound == 0 upper_bound == arr.length -1 return binary_search(arr, lower_bound, upper_bound, x)
Посчитаем сложность бинарного поиска:
Best case. Как и у линейного поиска, лучший случай равен O(1), ведь искомое число может находиться в середине массива, и тогда мы найдём его с первой попытки.
Worst case. Чтобы найти худший случай, нужно ответить на вопрос: «Сколько раз нужно разделить массив на 2, чтобы в нём остался один элемент?» Или найти минимальное число k, при котором справедливо 2^k ≥ n.
Надеюсь, что большинство читателей смогут вычислить k. Но на всякий случай подскажу решение: k = log n по основанию 2 (в алгоритмах практически все логарифмы двоичные). Поэтому worst case бинарного поиска — O(log n).
Average case. Он тоже равен O(log n). И если для линейного поиска average case в два раза лучше, чем worst case, то тут они обычно отличаются всего на несколько шагов.
Часто студенты спрашивают: «Зачем нужен линейный поиск, если бинарный обходит его по всем позициям?» Отвечаю: линейный поиск работает с любыми массивами, а бинарный — только с отсортированными.
Мы дошли до важного принципа: чем сложнее структура данных, тем более быстрые алгоритмы к ней можно применять. Отсортированный массив — более сложная структура, чем неотсортированный. Забегу вперёд и скажу, что сортировка в общем случае требует от O(n * log(n)) до O(n^2) времени.
Создать дополнительные структуры данных несложно, вот только это не бесплатное удовольствие. Они едят много памяти. Как правило, O(n). Отсюда вытекает довольно логичный, но обидный вывод: время и память — «взаимообмениваемые» ресурсы. Алгоритм можно ускорить, пожертвовав памятью, или решать задачу медленно, зато in-place. Кроме того, почти всегда есть промежуточный вариант.
Решить одну и ту же проблему зачастую можно тремя способами. Задача разработчика — выбрать самый подходящий.
Мы рассмотрели два алгоритма и увидели примеры их сложности. Но так и не поговорили о том, как эту сложность определять. Есть три основных способа.
Первый и наиболее часто используемый способ. Именно так мы определяли сложность linear search и binary search. Обобщим эти примеры.
Первый случай. Есть алгоритм some_function, который выполняет действие А, а после него — действие В. На А и В нужно K и J операций соответственно.
int some_function():
action_A() // K operations
action_B() // J operations
В случае последовательного выполнения действий сложность алгоритма будет равна O(K + J), а значит, O(max (K, J)). Например, если А равно n^2, а В — n, то сложность алгоритма будет равна O(n^2 + n). Но мы уже знаем, что нас интересует только самая быстрорастущая часть. Значит, ответ будет O(n^2).
Второй случай. Посчитаем сложность действий или вызова методов в циклах. Размер массива равен n, а над каждым элементом будет выполнено действие А (n раз). А дальше всё зависит от «содержимого» A.
Посчитаем сложность бинарного поиска:
int some_function(int [] arr): n = arr.length for i in 0..n: action_A() // K operations
Если на каждом шаге A работает с одним элементом, то, независимо от количества операций, получим сложность O(n). Если же A обрабатывает arr целиком, то алгоритм совершит n операций n раз. Тогда получим O(n * n) = O(n^2). По такой же логике можно получить O(n * log n), O(n^3) и так далее.
Третий случай — комбо. Для закрепления соединим оба случая. Допустим, действие А требует log(n) операций, а действие В — n операций. На всякий случай напомню: в алгоритмах всегда идёт речь о двоичных логарифмах.
Добавим действие С с пятью операциями и вот что получим:
int some_function(int [] arr): n = arr.length for i in 0..n: for j in 0..n: action_A(arr) // log(n) operations action_B(arr) // n operations action_C() // 5 operations
O(n * (n * log(n) + n) + 5) = O(n^2 * log(n) + n^2 + 5) = O(n^2 * log(n)).
Мы видим, что самая дорогая часть алгоритма — действие А, которое выполняется во вложенном цикле. Поэтому именно оно доминирует в функции.
Есть разновидность определения на глаз — амортизационный анализ. Это относительно редкий, но достойный упоминания гость. В двух словах его можно объяснить так: если на X «дешёвых» операций (например, с O(1)) приходится одна «дорогая» (например, с O(n)), то на большом количестве операций суммарная сложность получится неотличимой от O(1).
Частый пациент амортизационного анализа — динамический массив. Это массив, который при переполнении создаёт новый, больше оригинального в два раза. При этом элементы старого массива копируются в новый.
Практически всегда добавление элементов в такой массив «дёшево» — требует лишь одной операции. Но когда он заполняется, приходится тратить силы: создавать новый массив и копировать N старых элементов в новый. Но так как массив каждый раз увеличивается в два раза, переполнения случаются всё реже и реже, поэтому average case добавления элемента равен O(1).
Слабое место прикидывания на глаз — рекурсия. С ней и правда приходится тяжко. Поэтому для оценки сложности рекурсивных алгоритмов широко используют мастер-теорему.
По сути, это набор правил по оценке сложности. Он учитывает, сколько новых ветвей рекурсии создаётся на каждом шаге и на сколько частей дробятся данные в каждом шаге рекурсии. Это если вкратце.
Метод Монте-Карло применяют довольно редко — только если первые два применить невозможно. Особенно часто с его помощью описывают производительность систем, состоящих из множества алгоритмов.
Суть метода: берём алгоритм и гоняем его на случайных данных разного размера, замеряем время и память. Полученные измерения выкладываем на отдельные графики для памяти и времени. А затем автоматически вычисляется функция, которая лучше всего описывает полученное облако точек.
На протяжении всей статьи мы говорили про Big O Notation. А теперь сюрприз: это только одна из пяти существующих нотаций. Вот они слева направо: Намджун, Чонгук, Чингачгук… простите, не удержался. Сверху вниз: Small o, Big O, Big Theta, Big Omega, Small omega. f — это реальная функция сложности нашего алгоритма, а g — асимптотическая.
Несколько слов об этой весёлой компании:
- Big O обозначает верхнюю границу сложности алгоритма. Это идеальный инструмент для поиска worst case.
- Big Omega (которая пишется как подкова) обозначает нижнюю границу сложности, и её правильнее использовать для поиска best case.
- Big Theta (пишется как О с чёрточкой) располагается между О и омегой и показывает точную функцию сложности алгоритма. С её помощью правильнее искать average case.
- Small o и Small omega находятся по краям этой иерархии и используются в основном для сравнения алгоритмов между собой.
«Правильнее» в данном контексте означает — с точки зрения математических пейперов по алгоритмам. А в статьях и рабочей документации, как правило, во всех случаях используют «Большое „О“».
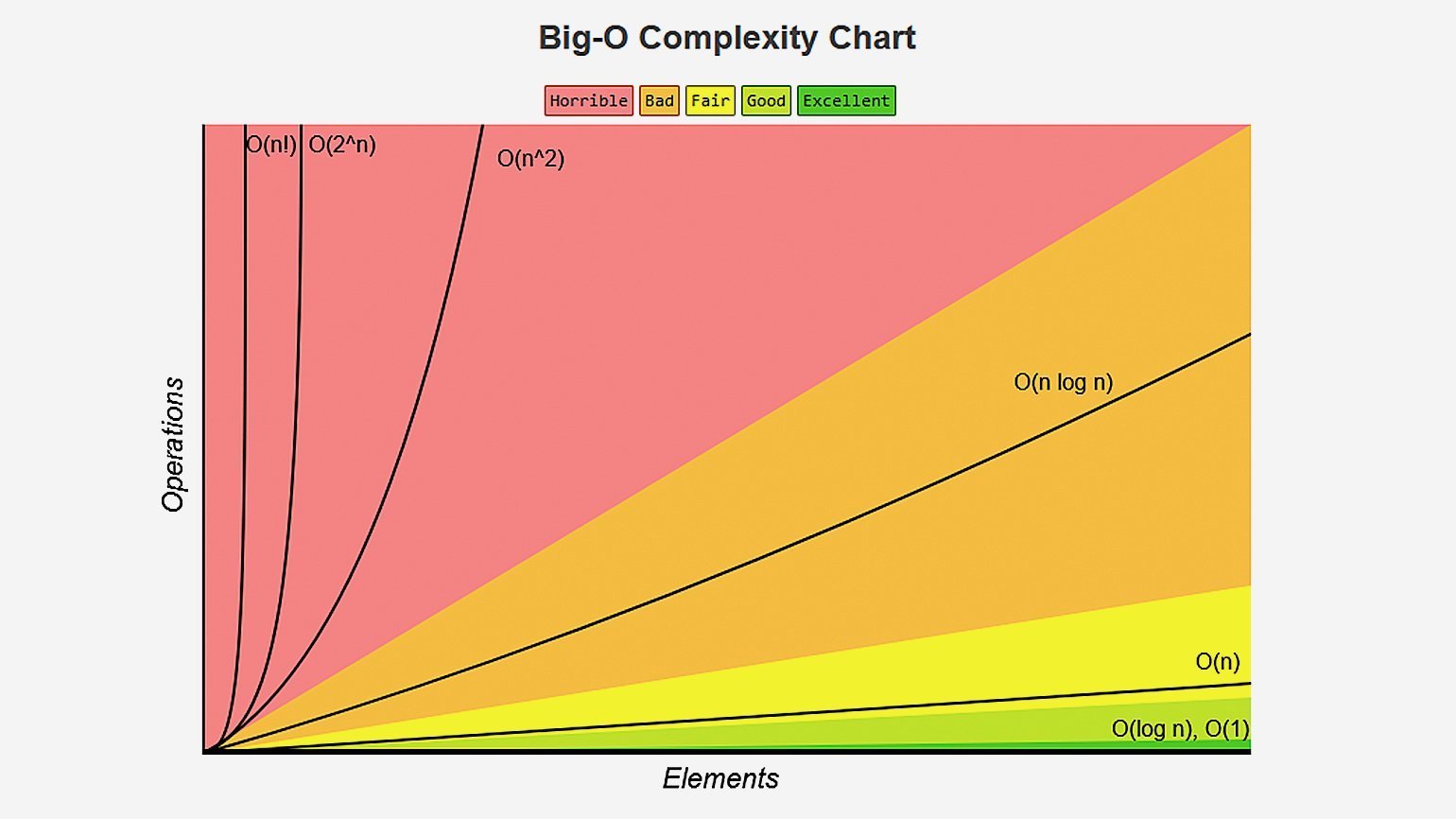
Если хотите подробнее узнать об остальных нотациях, посмотрите интересный видос на эту тему. Также полезно понимать, как сильно отличаются скорости возрастания различных функций. Вот хороший cheat sheet по сложности алгоритмов и наглядная картинка с графиками оттуда:
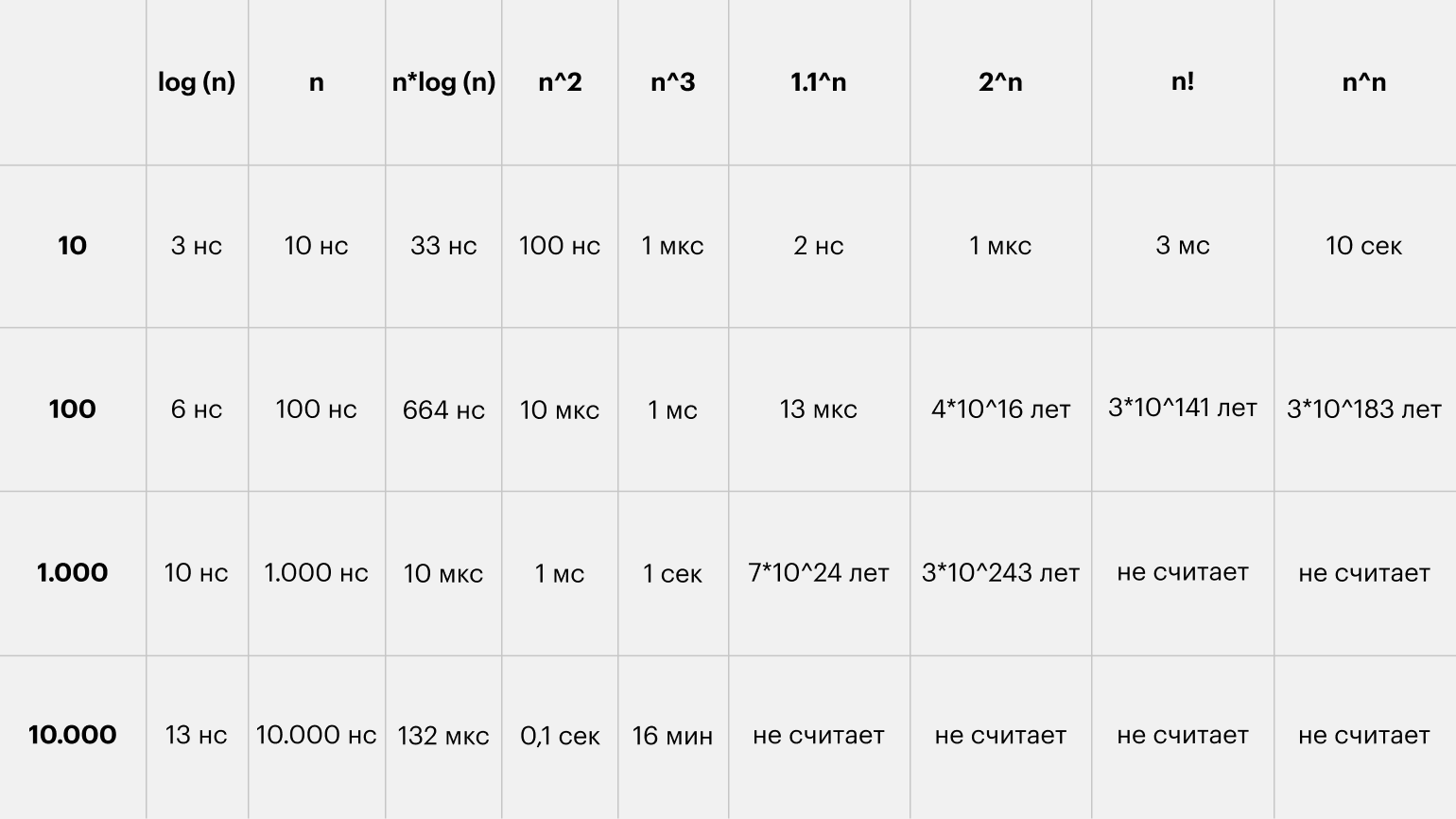
Хоть картинка и наглядная, она плохо передаёт всю бездну, лежащую между функциями. Поэтому я склепал таблицу со значениями времени для разных функций и N. За время одной операции взял 1 наносекунду:
В последнем разделе поговорим о скрытых константах. Это хитрая штука, там собака зарыта.
Возьмём умножение матриц. При размерности матрицы n * n наивный алгоритм, который многие знают с начальных курсов универа, «строчка на столбик» имеет кубическую временную сложность O(n^3). Кубическая, зато честная. Без констант и O(10000 * n^3) под капотом. И памяти не ест — только время.
У Валерия есть отдельный тред об умножении матриц.
В некоторых алгоритмах умножения матриц степень n сильно «порезана». Самые «быстрые» из них выдают время около O(n^2,37). Какой персик, правда? Почему бы нам не забыть про «наивный» алгоритм?
Проблема в том, что у таких алгоритмов огромные константы. В пейперах гонятся за более компактной экспонентой, а степени отбрасываются. Я не нашёл внятных значений констант. Даже авторы оригинальных пейперов называют их просто «очень большими».
Давайте от балды возьмём не очень большую константу 100 и сравним n^3 c 100 * n^2,37. Правая функция даёт выигрыш по сравнению с левой для n, начинающихся с 1495. А ведь мы взяли довольно скромную константу. Подозреваю, что на практике они не в пример больше…
В то же время умножение матриц 1495 × 1495 — очень редкий случай. А матрицы миллиард на миллиард точно нигде не встретишь. Да простит меня Император Душнил с «Хабра» за вольное допущение 
Такие алгоритмы называются галактическими, потому что дают выигрыш только на масштабах, нерелевантных для нас. А в программном умножении матриц, если я правильно помню курс алгоритмов и умею читать «Википедию», очень любят алгоритм Штрассена с его O(2,807) и маленькими константами. Но и те, к сожалению, жрут слишком много памяти.
Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.
Оценка сложности
Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.
Допустим, некоторому алгоритму нужно выполнить 4n3 + 7n условных операций, чтобы обработать n элементов входных данных. При увеличении n на итоговое время работы будет значительно больше влиять возведение n в куб, чем умножение его на 4 или же прибавление 7n. Тогда говорят, что временная сложность этого алгоритма равна О(n3), т. е. зависит от размера входных данных кубически.
Использование заглавной буквы О (или так называемая О-нотация) пришло из математики, где её применяют для сравнения асимптотического поведения функций. Формально O(f(n)) означает, что время работы алгоритма (или объём занимаемой памяти) растёт в зависимости от объёма входных данных не быстрее, чем некоторая константа, умноженная на f(n).
Примеры
O(n) — линейная сложность
Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.
O(log n) — логарифмическая сложность
Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.
O(n2) — квадратичная сложность
Такую сложность имеет, например, алгоритм сортировки вставками. В канонической реализации он представляет из себя два вложенных цикла: один, чтобы проходить по всему массиву, а второй, чтобы находить место очередному элементу в уже отсортированной части. Таким образом, количество операций будет зависеть от размера массива как n * n, т. е. n2.
Бывают и другие оценки по сложности, но все они основаны на том же принципе.
Также случается, что время работы алгоритма вообще не зависит от размера входных данных. Тогда сложность обозначают как O(1). Например, для определения значения третьего элемента массива не нужно ни запоминать элементы, ни проходить по ним сколько-то раз. Всегда нужно просто дождаться в потоке входных данных третий элемент и это будет результатом, на вычисление которого для любого количества данных нужно одно и то же время.
Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.
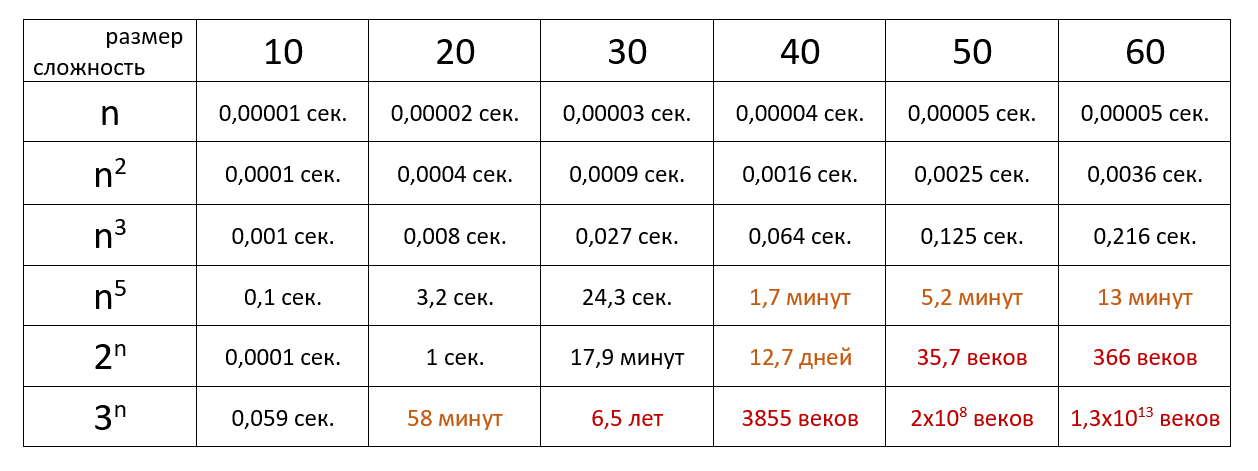
Наглядно
Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 106 операций в секунду:
Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».