Резервы времени построенного сетевого
графика оценивают только для некритических
работ, так как для работ, лежащих на
критическом пути все резервы равны
нулю.
Можно рассчитать четыре вида резервов
времени выполнения работы
:
1) полный резерв:
;
2)
гарантированный резерв:
;
3) свободный резерв:
;
4) независимый резерв:
Полный резерв – это максимальное время,
на которое можно перенести начало работы
или увеличить продолжительность работы
без изменения общего срока выполнения
комплекса работ.
Полный резерв времени определяется как
резерв времени максимального пути,
проходящего через эту работу.
Если полный резерв времени работы
использовать именно для этой работы,
то все остальные работы максимального
пути, проходящего через эту работу,
резервов времени иметь не будут.
Гарантийный резерв есть часть полного
резерва времени этой работы за вычетом
резерва времени работ, предшествующих
событию.
Свободный резерв представляет собой
максимальное время, на которое можно
отсрочить начало или увеличить
продолжительность работы
при условии, что все события сети
наступают в свои ранние сроки. Этот
резерв – часть полного резерва.
Использование резерва одной работы
может уменьшать резервы последующих
или предыдущих работ. Иногда
продолжительность времени выполнения
работы может быть увеличена без изменения
резервов времени предшествующих и
последующих работ. Такое возможное
увеличение времени работы называется
независимым резервом времени (если НР
получается отрицательным, то его нужно
считать нулевым).
В отличие от полного резерва времени,
который в случае его использования
отнимает резервы времени работ, лежащих
на предшествующем и последующем отрезках
максимального пути, проходящего через
эту работу, независимый резерв времени
работы
принадлежит только для данной работы.
Его нельзя передать ни предшествующим,
ни последующим работам, находящимся на
ее максимальном пути, проходящим через
эту работу.
Использование независимого резерва
времени на работе, которая его имеет,
не влияет на ранние и поздние сроки
свершения всех событий и работ сети.
Независимый резерв времени работы
представляет собой остаток от ее полного
резерва времени, если за счет последнего
полностью сохранены резервы времени
начального и конечного событий данной
работы. Таким образом, величина
независимого резерва времени работы
показывает продолжительность вынужденного
ожидания наступления конечного события
данной работы, что позволяет снять с
этой работы часть ресурсов, чтобы
перебросить их на более напряженные
работы.
На критическом пути резервов времени
для выполнения работы нет. Следовательно,
задержка в выполнении какой-либо одной
работы приведет к задержке выполнения
всего комплекса работ. Следовательно,
руководителю необходимо следить за
выполнением работ, составляющих
критический путь, в первую очередь,
выделяя для него ресурсы – трудовые и
материальные. Работы, лежащие не на
критическом пути, имеют достаточный
резерв времени, значит, их выполнение
можно отнести на период менее загруженный,
и контролировать их выполнение выборочно
или возложить на подчиненных руководство
ими.
Сетевой график может быть оптимизирован,
т.е. разработан новый план, в соответствии
с которым комплекс работ может быть
выполнен с меньшей затратой материальных
средств или в более короткие сроки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
[c.312]
Критический путь в сетевом графике имеет максимальную продолжительность. Разница между продолжительностью критического пути Гкр и продолжительностью любого другого пути Т (Ln) является общим полным резервом времени пути [c.49]
На рис. 7.6 показан сетевой график, в котором пути, проходящие через работы 0,2 и 2,6 0,1 и 1,3 0,1—1,4— 4,5, имеют одинаковый полный резерв времени (30 дней). Однако коэффициенты напряженности путей, проходящих через эти работы, будут совершенно различными. Соответственно /z,u= 150/180 = 0,833 /г 2 = 30/60 = 0,5 kn3 = = 90/120 = 0,75. Поэтому в случае последующей оптимизации сетевого графика (при прочих равных условиях, например одинаковом составе ресурсов) в первую очередь целесообразно изъять резервы с пути 0,1 и 1,3 как менее напряженного (Ан2 = 0,5). Уменьшение резерва, допустим, на 20 дней сделает первый и третий пути совсем близкими к критическому ( = 170/180=0,944 kB3 110/120— = 0,917), а второй — еще имеющим довольно ощутимые резервы ( П2=50/60=0,833).
[c.234]
Для определения полного резерва времени пути R(Lt) следует опять вернуться к тому условию, что длина критического пути в сетевом графике больше, чем длина любого другого полного пути. Разница между длиной критического пути г(1 р) и длиной анализируемого пути t(L,) называется полным резервом времени пути L [c.40]
Наиболее важная из проблем, которые приходится решать при осуществлении комплекса работ, — это распределение ресурсов между отдельными работами. Дело в том, что для проведения работ необходимо обеспечить их трудовыми и материальными ресурсами. Количество ресурсов различных типов, находящихся в распоряжении руководителя работ по проекту, обычно бывает ограничено. Очень часто этих ресурсов не хватает чтобы обеспечить завершение всех работ Рц в наиболее ранние моменты, которые равны ti + tij. В этом случае расчет резервов времени Мц и Мц для каждой работы позволяет определить, какие из работ PI/ должны получить ресурсы и быть начаты сразу после совершения предшествующих им событий (, а какие могут быть задержаны без ущерба для сроков осуществления проекта. Изложенные здесь соображения можно использовать как при предварительном планировании расписания выполнения работ, так и при оперативном управлении, когда ситуация с работами меняется, случаются задержки работ сверх полного резерва времени М] , что приводит к изменению критического пути и необходимости срочного перераспределения ресурсов между работами. Пересчет сетевого графика на ЭВМ, т. е. определение новых значений резервов времени, дает возможность быстро осуществить эту операцию.
[c.190]
Известно, что в сетевом графике длина критического пути больше длины любого другого пути. Разница между этими длинами называется полным резервом времени пути. Этот резерв R (L) определяется зависимостью
[c.367]
Для ликвидации отставаний от графика в первую очередь необходимо использовать резервы времени. Применение сетевых методов в оперативном управлении позволяет в полной мере вскрыть и мобилизовать этот вид резервов. Без использования сетевых моделей выявить имеющиеся по различным операциям технологического процесса резервы времени зачастую вообще не представляется возможным. Важнейшее преимущество сетевых моделей — строгая взаимоувязка сроков выполнения всего комплекса работ. Возможности использования различных видов резервов времени по работам сетевых графиков подробно рассматривались при построении перспективных вариантов очередности запуска в производство серий изделий.
[c.139]
Критический путь, т.е. полный путь, на котором суммарная продолжительность работ является максимальной. Иными словами, это самый длинный по времени путь в сетевом графике от исходного до завершающего события. Критический путь лимитирует выполнение задачи в целом, поэтому любая задержка на работах критического пути увеличивает время всего процесса. События, через которые проходит критический путь в работы, выполняемые не на критических путях, называются ненапряженными. У критических работ как полные, так и свободные резервы времени равны нулю (признак критической работы). Критический путь рассчитывается путем определения работ, полные резервы времени которых равны нулю.
[c.168]
В сетевом планировании различают полный / ,- / и частный Л -j резервы времени работ. Полный резерв времени работы — это разность между поздним и ранним сроками начала (или окончания) работы. Это тот запас времени, который может быть использован на данной работе (посредством перенесения срока начала или увеличения продолжительности работы) без ущерба для конечного срока всего комплекса, но при использовании которого последующие работы выполняются в свои поздние допустимые сроки, т. е. лишаются резерва времени. Полный резерв примени-
[c.75]
Поскольку возможно использование полных резервов времени работ не во всем их объеме, а только частично, то возникают различные варианты выполнения намеченного плана. Методологией сетевого планирования они предусмотрены в других резервах времени работ. Так, выделяют частный резерв времени первого вида, частный резерв времени второго вида и независимый резерв времени. Все они являются частями полного резерва времени и позволяют осуществлять более тонкое маневрирование ограниченными ресурсами в процессе выполнения всего комплекса работ без нарушения времени критического пути. О них можно прочитать в специальной литературе по экономико-математическим методам.
[c.528]
Совершенно очевидно, что, располагая такой небольшой бригадой, состоящей лишь из отца и сына, объем работ, отраженный на рис. 7.6, не может быть выполнен. Календарный план должен быть перестроен так, чтобы имеющиеся скромные ресурсы не накладывались друг на друга. Используя регулируемый график, нужно переставлять операции до тех пор, пока в каждой колонке не окажется число, не превышающее число имеющихся доступных рабочих (1 квалифицированный и 1 чернорабочий). Когда эта перестановка осуществится, необходимо вспомнить о логике сетевой модели, на основе которой была построена данная гистограмма, и обо всех наблюдаемых ограничениях но некоторые работы, возможно, придется отложить на срок, превышающий их полный резерв времени, и, таким образом, длительность проекта может увеличиться.
[c.125]
В сетевой модели можно выделить так называемый критический путь. Критический путь LKp состоит из работ (i,j), у которых полный резерв времени равен нулю Rn(i, j) = 0, кроме этого, резерв времени R(f) всех событий i на критическом равен 0. Длина критического пути определяет величину наиболее длинного пути от начального до конечного события сети и равна
[c.28]
Резервы времени работ на сетевых графиках изображаются дробью под стрелкой (работой) полный резерв — в числителе, свободный — в знаменателе.
[c.50]
Резервы времени работ изображаются на сетевых графиках п од стрелками дробью полный резерв — в числителе, свобод- ный — в знаменателе.
[c.54]
Полный список операций для дальнейшей обработки передается в вычислительную группу или обрабатывается на месте вручную. В процессе расчета определяются начало и окончание работ, критический путь и резервы времени с уточнением календарных дат. При расчетах сетевых графиков наибольшее распространение получили следующие обозначения [c.92]
В сетевых графиках имеются и другие пути, опирающиеся на исходное и завершающее события (полные пути), которые могут либо полностью проходить вне критического пути, либо частично совпадать с критической последовательностью работ. Эти пути называются ненапряженными, по продолжительности они меньше критического пути. Ненапряженные пути обладают тем свойством, что на участках, не совпадающих с критической последовательностью работ, они имеют резервы времени. Это означает, что задержка в наступлении событий, не
[c.38]
В качестве базовой методики вычисления главных показателей графика проекта используется хорошо зарекомендовавший себя метод критического пути — основа методов сетевого планирования и управления. Под методом критического пути понимают совокупность методик и формул сетевого планирования и управления, обеспечивающих автоматическое вычисление для всех работ графика моментов раннего и позднего начала, раннего и позднего окончания, а также полных и свободных резервов времени. Работы, имеющие отрицательный или нулевой резерв времени, считают находящимися на критическом пути. Часто в состав критического пути включают работы, имеющие достаточно малый резерв времени, не превосходящий некоторой заранее заданной малой положительной вели-
[c.28]
Изменяют топологию всего сетевого графика, т. е. технологию выполнения работ. Это возможно потому, что отдельные работы можно выполнять различными способами. Выбирают такой вариант, при котором работы, ранее выполняемые последовательно, могли быть выполнены параллельно. Параллельности можно добиться также путем расчленения работ большой продолжительности на более мелкие работы, что дает возможность последующую работу начать до полного окончания предшествующей. В ряде случаев изменение технологии позволяет заменить некоторые работы, лежащие на критическом пути, работами другого содержания, требующими меньших затрат времени. Оптимизированный вариант сетевого графика является документом, по которому осуществляется оперативное управление всем комплексом работ. Предположим, что директивный срок,монтажа компрессора — 20 дней. Полученная продолжительность критического пути составила 22 дня, т. е. сетевой график должен быть сжат на 2 дня. Некритическая работа 1—3 имеет резерв 5 дней. Целесообразно резервы данной работы перебросить на критическую работу 1—4. Удлинив работу 1—3 до 6 дней сокращаем работу 1—4 на 2 дня, сократив, таким образом, критический путь до 20 дней, что соответствует директивному сроку.
[c.211]
Таким образом, резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения всего комплекса работ. Критические события резервов времени не имеют, так как любая задержка в совершении события, лежащего на критическом пути, вызовет такую же задержку в совершении события всего комплекса работ. Из этого следует, что топологию критического пути можно определить не обязательно посредством перебора всех полных путей сетевого графика, что иногда может оказаться утомительным, а просто посредством выявления всех событий, имеющих нулевые резервы времени.
[c.526]
Каждая работа, как и пути, в которые она входит, имеет резервы времени. Резерв времени любого полного пути сетевого графика представляет собой разность между длиной критического пути и длиной данного пути [c.527]
После составления сетевого графика производится его расчет, в результате которого определяются основные параметры графика — раннее начало и раннее окончание работ, позднее начало и позднее окончание их, полный и свободный резервы времени работ, направление и продолжительность
[c.22]
Резервы времени удобно рассчитывать по сетевому графику, так как величины Tf, Tf записаны в его вершинах. Полученные значения резервов записывают около соответствующих дуг сетевого графика. Сначала ставят полный резерв, а затем свободный.
[c.280]
Срок свершения 2-го, седьмого, двенадцатого, тринадцатого событий рассчитывается по максимальному из предшествующих ему путей. Срок свершения события 2 равен 10 дням (2+6+2), события 7—17 (2 + 6 + 2 + 7), события 12—18 (2+6 + 2 + 7+1), события 13—22(2+6 + 2 + 7+1+4). Значит, ранний срок свершения завершающего события — 22 дня, что соответствует величине, подсчитанной при определении полных путей и критического пути сетевого графика. В рассматриваемом сетевом графике поздний срок свершения последнего события 13 составляет 22 дня. Поздний срок свершения события 12 определяется вычитанием из позднего срока свершения события 13 продолжительности работы, ведущей от события 12 к событию 13, что составит 18 дней (22—4). Таким же образом устанавливаются поздние сроки свершения и всех остальных событий, кроме 1 и 9. После события 1 следует четыре работы работа 1—3, 1—2, 1—4, 1—5. В подобных случаях выбирается минимальная по продолжительности разность между поздним сроком свершения последующего события и сроком выполнения работы, ведущей от данного события к последующему. Отсюда поздний срок свершения события 1 составит 2 дня. Тп события 4 равен 8—22—(4 + 1+7+2). Принимаем срок в 2 дня, поскольку эта величина меньше возможных других трех величин, так как, если берем путь 1—3, то поздний срок свершения события 1 будет равен 22—(2 + 5 + 3+1)—4 = 7 дней, путь 1—2 —22—(4 + 1+7)—3 = 7дней, путь 1—5 22—(4 + 3 + 4 + +5)—2=4 дня. Аналогично этому ранний срок свершения события составит 22—(4 + 3-)—4 = 11 дней, так как, идя другим путем, величина Тп для события 9 будет больше 22—(4 + 1)—3 = = 14 дней. Разность между поздним и ранним сроками устанавливает резерв времени. Для события 1 резерв составит 0(2—2), для события 2 — также 0(10—10), для события 3—5 дней (11—6), события 4—0 (8—8), события 5—0 (4—4), события 6—5 дней (12—7), события 7—0(17—17), события 8—5 дней (15—10), события 9—2 дня (11—9), события 10—5 дней (20—15), события 11—2 дня (15—13), события 12—0 (18—18), события 13—0 (22—22). Так как критический путь проходит через события с нулевыми резервами времени, его продолжительность может быть определена как сумма времени свершения событий 1, 2, 4, 7, 12, 13, что совпадает с ранее сделанными расчетами длительности критического пути.
[c.209]
Вместо календаризации сетевых графиков их часто перестраивают в обычные линейные календарные графики по ранним началам работ с нанесением полных и свободных резервов времени.
[c.40]
Определение критического пути
Полный путь,
суммарная продолжительность работ на котором является
максимальной, называется критическим, то есть это самый длинный
по времени путь в сетевом графике от исходного события до завершающего.
Продолжительность критического пути определяет минимальное время,
объективно необходимое для выполнения всего комплекса мероприятий,
входящих в планируемый процесс. За время, меньше времени критического
пути, весь комплекс мероприятий совершиться не может. Поэтому любая
задержка на работах критического пути увеличивает время выполнения всего
процесса.
События,
через которые проходит критический путь, называются критическими. Работы, входящие в состав критического пути,
называются критическими.
Задержка в выполнении работы на величину 
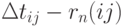
Задержка в выполнении работы на величину 
графиком. Следовательно, у критических работ и полные, и свободные резервы
времени равны нулю. Вообще говоря, равенство нулю полного резервного
времени работы является необходимым и достаточным признаком того, что
данная работа критическая. Напротив, свободный резерв времени может быть
равным нулю и у некритических работ.
Таким образом, критический путь находится посредством определения работ,
полные резервы времени которых равны нулю.
Определение полного резерва времени ненапряженного пути
События и
работы, лежащие не на критических путях (такие пути называются ненапряженными ), обладают резервами времени. Выявление этих
резервов наравне с определением критического пути составляет основное
содержание анализа сетевой модели. С работ и путей, имеющих резервы
времени, можно снять ресурсы и направить их на выполнение работ, лежащих
на критических путях. Этим самым можно добиться сокращения сроков
проведения критических работ, а следовательно, и всей операции в целом,
используя только внутренние резервы.
Полным резервом времени ненапряженного пути
называется разница между его длиной и длиной критического пути. Полный резерв времени
ненапряженного пути показывает, на сколько в сумме может быть увеличена
продолжительность всех работ этого пути без изменения срока выполнения
всего процесса в целом. Однако при этом ненапряженный и критический пути
не должны пересекаться. Если они пересекаются, то полный резерв времени
определяется самым длительным участком напряженного пути, заключенным
между соответствующими парами событий критического пути.
Формирование временных оценок работ
Адекватность сетевой модели отображаемому реальному процессу и,
соответственно, оперативность руководства процессом во многом зависят от
правильности временных оценок выполняемых работ. Если, например,
продолжительность работ будет занижена, то это вызовет поспешность в
подготовке всей операции в целом, что, в свою очередь, может привести к
срыву и цель не будет достигнута. А завышение сроков выполнения отдельных
работ может привести к потере времени, что также, как правило, ведет к
срыву.
Для определения временных и других характеристик, необходимых для оценки
длительности работ или расхода ресурсов, могут использоваться
статистические данные, полученные опытным путем. Такие оценки однозначно
определяются из нормативов. Если такие нормативы отсутствуют, то
разработчиками сетевого графика даются три оценки времени:
Оптимистическая оценка — продолжительность работы в наиболее
благоприятных условиях.
Пессимистическая оценка — продолжительность работы при самом
неблагоприятном стечении обстоятельств.
Наиболее вероятная оценка — продолжительность работы при условии, что
не возникнет никаких неожиданных трудностей.
На основании этих оценок вычисляются оценки 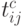
дисперсии 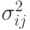
 |
( 14.6) |
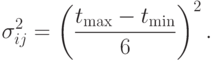 |
( 14.7) |
В этом случае все расчеты проводятся так, как было рассмотрено выше. Затем
рассчитываются вероятности того, что полученные параметры сетевой модели
(ранние сроки, поздние сроки, резервы и т.д.) действительно будут
находиться в тех или иных числовых границах. При этом вводится допущение,
что продолжительности двух любых работ являются независимыми величинами,
а величина 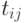
равной математическому ожиданию продолжительности данной работы ( 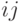
Тогда математическое ожидание любого параметра сетевой модели, являющегося
суммой величин вида 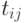
слагаемых, то есть 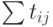
все параметры сетевой модели носят, так сказать, экстремальный характер.
Соответственно, дисперсия параметра будет 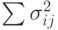
Если считать, что время выполнения работ подчиняется нормальному закону,
вероятность совершения 
определить по следующей формуле:
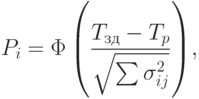 |
( 14.8) |
где 
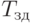


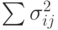
использовались при вычислении раннего срока наступления 



