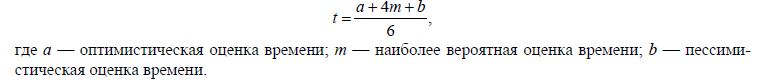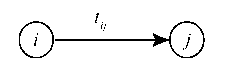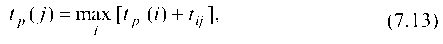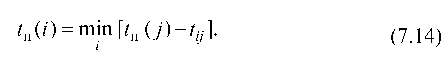Полный резерв времени выполнения работы проекта спу равен разности между

Методы
СПУ используются при планировании
сложных комплексных проектов, например,
таких как [Вентц]:

• строительство
  и реконструкция каких-либо объектов;

• выполнение
  научно-исследовательских и конструкторских
  работ;

• подготовка
  производства к выпуску продукции;

• перевооружение
  армии;

• развертывание
  системы медицинских или профилактических
  мероприятий.

Характерной
особенностью таких проектов является
то, что они состоят из ряда отдельных,
элементарных работ.
Они обуславливают друг друга так, что
выполнение некоторых работ не может
быть начато раньше, чем завершены
некоторые другие. Например, укладка
фундамента не может быть начата раньше,
чем будут доставлены необходимые
материалы; эти материалы не могут быть
доставлены раньше, чем будут построены
подъездные пути; любой этап строительства
не может быть начат без составления
соответствующей технической документации
и т.д.

СПУ состоит из трех основных
этапов [Таха].

1. Структурное
   планирование.

2. Календарное
   планирование.

3. Оперативное
   управление.

Структурное
планирование
начинается с разбиения проекта на четко
определенные операции, для которых
определяется продолжительность. Затем
строится сетевой график, который
представляет взаимосвязи работ проекта.
Это позволяет детально анализировать
все работы и вносить улучшения в структуру
проекта еще до начала его
реализации.

Календарное
планирование
предусматривает построение календарного
графика, определяющего моменты начала
и окончания каждой работы и другие
временные характеристики сетевого
графика. Это позволяет, в частности,
выявлять критические операции, которым
необходимо уделять особое внимание,
чтобы закончить проект в директивных
срок. Во время календарного планирования
определяются временные характеристики
всех работ с целью проведения оптимизации
сетевой модели, которая улучшает
эффективность использования какого-либо
ресурса.

В ходе оперативного
управления
используются сетевой и календарных
графики для составления периодических
отчетов о ходе выполнения проекта. При
этом сетевая модель может подвергаться
оперативной корректировке, вследствие
чего будет разрабатываться новый
календарный план остальной части
проекта.

1.2. СТРУКТУРНОЕ
ПЛАНИРОВАНИЕ

Основными понятиями
сетевых моделей являются понятия события
и работы.

Работа — это
некоторый процесс, приводящий к достижению
определенного результата и требующий
затрат каких-либо ресурсов, имеет
протяженность во времени.

По своей
физической природе работы можно
рассматривать как:

• действие:
  заливка фундамента бетоном, составление
  заявки на материалы, изучение конъюнктуры
  рынка;

• процесс:
  старение отливок, выдерживание вина,
  травление плат;

• ожидание:
  ожидание поставки комплектующих,
  пролеживание детали в очереди к станку.

По
количеству затрачиваемого времени
работа может быть:

• действительной,
  т.е. требующей затрат времени: ;

• фиктивной,
  не требующей затрат времени и
  представляющей связь между какими-либо
  работами: передача измененных чертежей
  от конструкторов к технологам, сдача
  отчета о технико-экономических
  показателях работы цеха вышестоящему
  подразделению.

Событие — момент
времени, когда завершаются одни работы
и начинаются другие. Событие представляет
собой результат проведенных работ и, в
отличие от работ, не имеет протяженности
во времени. Например, фундамент залит
бетоном, старение отливок завершено,
комплектующие поставлены, отчеты сданы
и т.д.

Таким образом, начало и
окончание любой работы описываются
парой событий, которые называются
начальным
и конечным
событиями. Поэтому для идентификации
конкретной работы используют код работы
(i,j), состоящий из номеров начального
(i-го) и конечного (j-го) событий, например
(2,4); 3-8; 9,10.

На
этапе структурного планирования
взаимосвязь работ и событий изображаются
с помощью сетевого графика, где работы
изображаются стрелками, которые соединяют
вершины, изображающие события. Работы,
выходящие из некоторого события не
могут начаться, пока не будут завершены
все операции, входящие в это
событие.Событие,
не имеющее предшествующих ему событий,
т.е. с которого начинается проект,
называютисходным,
событие.
Событие, которое не имеет последующих
событий и отражает конечную цель проекта,
называется завершающим.

При
построении сетевого графа необходимо
следовать следующим правилам:

• длина
  стрелки не зависит от времени выполнения
  работы;

• стрелка
  не обязательно должна представлять
  прямолинейный отрезок;

• для
  действительных работ используются
  сплошные, а для фиктивных — пунктирные
  стрелки;

• каждая
  операция должна быть представлена
  только одной стрелкой;

• не
  должно быть параллельных работ между
  одними и теми же событиями, для избежания
  такой ситуации используют фиктивные
  работы;

• следует
  избегать пересечения стрелок;

• не
  должно быть стрелок, направленных
  справа налево;

• номер
  начального события должен быть меньше
  номера конечного события;

• не
  должно быть висячих событий, кроме
  исходного;

• не
  должно быть тупиковых событий, кроме
  завершающего;

• не
  должно быть циклов.

Поскольку
работы, входящие в проект могут быть
логически связаны друг с другом, то
необходимо всегда перед построением
сетевого графика дать ответы на следующие
вопросы

• Какие
  работы необходимо завершить непосредственно
  перед началом рассматриваемой работы?

• Какие
  работы должны непосредственно следовать
  после завершения данной работы?

• Какие
  операции могут выполняться одновременно
  с рассматриваемой работой?

Пример
построения сетевого графика

Пусть
необходимо спроектировать, изготовить
и сдать в эксплуатацию стенд согласно
полученному техническому заданию (ТЗ).
Известно, что для этого необходимо
выполнить следующие работы.

Кроме
того известно, что

• информация
  о характеристиках стенда может быть
  получена только в процессе создания
  электрической и механической частей
  стенда и после получения покупных
  элементов;

• рабочая
  документация по эксплуатации стенда
  может быть разработана и без проведения
  сборки самого стенда;

• контрольные
  испытания должны проводиться при
  наличии готовой документации по
  эксплуатации.

Кроме
того известно, что

• информация
  о характеристиках стенда может быть
  получена только в процессе создания
  электрической и механической частей
  стенда и после получения покупных
  элементов;

• рабочая
  документация по эксплуатации стенда
  может быть разработана и без проведения
  сборки самого стенда;

контрольные
испытания должны проводиться при наличии
готовой документации по эксплуатации.

1.3.
КАЛЕНДАРНОЕ ПЛАНИРОВАНИЕ

Применение
методов СПУ в конечном счете должно
обеспечить получение календарного
плана, определяющего сроки начала и
окончания каждой операции. Построение
сети является лишь первым шагом на пути
к достижению этой цели. Вторым шагом
является расчет сетевой модели, который
выполняют прямо на сетевом графике,
пользуясь простыми правилами.

Показать
расчет временных параметров событий
на примере.

К
временным параметрам событий относятся:

• ранний
  срок наступления события i —
  ;

• поздний
  срок наступления события i —
  ;

• резерв
  времени наступления события i —
  .

—
это время, необходимое для выполнения
всех работ, предшествующих данному
событию i.—
это такое время наступления события i,
превышение которого вызовет аналогичную
задержку наступления завершающего
события сети.—
это такой промежуток времен, на который
может быть отсрочено наступление этого
события без на рушения сроков завершения
разработки в целом.

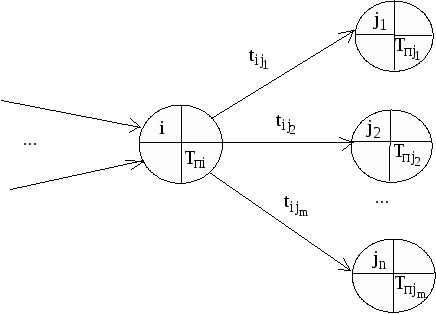
Значения временных
параметров записываются прямо в вершины
на сетевом графике следующим
образом.МЕТОДИКА
РАСЧЕТА ВРЕМЕННЫХ ПАРАМЕТРОВ
СОБЫТИЙ

Расчет ранних сроков
свершения событий ведется от исходного
к завершающему событию.

1) Для
исходного события.

1. Для
   всех остальных событий
   ,
   где максимум берется по всем работам,
   входящим в событие i.

Поздние
сроки свершения событий рассчитываются
от завершающего к исходному событию.

3)
Для завершающего события.

1. ,
   где минимум берется по всем работам,
   выходящим из события i.

5).

На
основе ранних и поздних сроков событий
можно определить временные параметры
работ сети.Показать
расчет временных параметров работ на
примере.

При
составлении таблицы, для записи временных
параметров работ, обычно коды работ
записывают в определенном порядке
[ксерокс]. Сначала записываются все
работы, выходящие из исходного, первого,
события, затем — выходящие из второго
события, потом — из третьего и т.д.

К
наиболее важным временным параметрам
работы относятся:

• ранний
  срок начала работы
  ;

• поздний
  срок начала работы
  ;

• ранний
  срок окончания работы
  ;

• поздний
  срок окончания работы
  ;

• полный
  резерв
  ;

• свободный
  резерв
  .

МЕТОДИКА
РАСЧЕТА ВРЕМЕННЫХ ПАРАМЕТРОВ РАБОТ

1. ;

2. или;

3. или;

4. ;

5. ;

6. .

Путь
— это любая последовательность работ в
сетевом графике, в которой конечное
событие одной работы совпадает с
начальным событием следующей за ней
работы.

Например, в рассмотренном
сетевом графике путями являются следующие
последовательности работ:

2-3, 3-4, 4-7
или 2,3,4,7;

8-9 или 8,9;

1-2, 2-3, 3-6, 6-7,
7-9, 9-10 или 1,2,3,6,7,9,10.

Полный
путь
— это путь от исходного до завершающего
события, например 1,2,3,6,7,9,10.

Критический
путь
— максимальный по продолжительности
полный путь.

Подкритический
путь
— полный путь, ближайший по длительности
к критическому пути.

Работы, лежащие
на критическом пути, называют критическими.
Они имеют ряд особенностей:

• начальные
  и конечные события критических работ
  имеют нулевые резервы событий;

• временно
  пропустить (это касается соотношения
  между
  и
  ,
  а также между
  и).

• временно
  пропустить (о значениях резервов работ).

Первую
особенность критических работ можно
использовать при поиске критического
пути. Для этого надо выявить все события,
имеющие нулевой резерв. В рассматриваемом
примере это события 1,2,3,4,7,8,9,10. Но через
эти события проходят три пути:

1. 1,2,8,9,10;

2. 1,2,3,4,7,8,9,10;

3. 1,2,3,4,7,9,10.

Непосредственное
суммирование длительностей работ этих
путей показывает, что путь 1) не является
критическим, несмотря на то, что лежащие
на нем события имеют нулевой резерв.
Отсюда следует вывод, что требование
нулевых резервов событий является
необходимым, но не достаточным условием
критического пути.

Дополнительное
задание: сформулировать достаточное
условие для определения критического
пути.

Разность
между продолжительность критического
пути
и
продолжительностью любого другого путиназывается
полным резервом времени пути L, т.е..
Этот резерв показывает, на сколько в
сумме может быть увеличена продолжительность
всех работ данного пути L, чтобы при этом
не изменился общий срок окончания всех
работ, т.е.[ксерокс].показывает
максимальное время, на которое может
быть увеличена продолжительность работыили
отсрочено ее начало, чтобы продолжительность
проходящего через нее максимального
пути не превысила продолжительности
критического пути. Важнейшее свойство
полного резерва работызаключается
в том, что если его использовать частично
или полностью, то уменьшится полный
резерв у работ, лежащих с работойна
одних путях. Т.о. полный резерв времени
принадлежит не одной данной работе,
а всем работам, лежащим на путях,
проходящим через эту работу
[Голенко].Пример
на сетевом графике

показывает
максимальное время, на которое можно
увеличить продолжительность отдельной
работы или отсрочить ее начало, не меняя
ранних сроков начала последующих работ,
при условии, что непосредственно
предшествующее событие наступило в
свой ранний срок. Использование свободного
времени на одной из работ не меняет
величины свободных резервов времени
остальных работ сети.Пример
на сетевом графике

Дополнительное
задание: обуславливает ли нулевой полный
резерв работы
нулевой
свободный резерв этой работы и
наоборот

обуславливает
ли нулевой свободный резерв работы
нулевой
полный резерв этой работы. Аргументировать
ответ и привести пример.

Конечным
результатом выполняемых на сетевой
модели расчетов является календарный
график [Таха], который иногда называют
графиком
привязки.

График
привязки
отображает взаимосвязь выполняемых
работ во времени и строится на основе
данных о ранних сроках начала и окончания
работ. Для удобства дальнейшей работы
на этом графике могут быть указаны
величины полных и свободных резервов
работ. По вертикальной оси графика
привязки откладываются коды работ, по
горизонтальной оси — длительность работ
(раннее начало и раннее окончание
работ).

График привязки можно
построить без предварительного расчета
ранних сроков начала и окончания всех
работе, используя только данные о
продолжительности работ. При этом
необходимо помнить, что работа
может
начать выполняться только после того
как будут выполнены все предшествующие
ей работы.Пример
построения графика привязки

Построим
график привязки для следующих исходных
данных.

Рис.1Рис.2

Практическая
ценность графика привязки заключается
в том, что с его помощью можно улучшать
эффективность использования ресурса
рабочей силы, т.е. проводить оптимизацию
сетевой модели.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Назначение и области применения сетевого планирования и управления

Поиски более эффективных способов планирования сложных процессов привели к созданию принципиально новых методов сетевого планирования и управления (СПУ).

Система методов СПУ — система методов планирования и управления разработкой крупных народнохозяйственных комплексов, научными исследованиями, конструкторской и технологической подготовкой производства, новых видов изделий, строительством и реконструкцией, капитальным ремонтом основных фондов путем применения сетевых графиков.

Первые системы, использующие сетевые графики, были применены в США в конце 50-х годов ХХ в. и получили названия СРМ (английская аббревиатура, означающая метод критического пути) и PERT (метод оценки и обзора программы). Система СРМ была впервые применена при управлении строительными работами, система PERT — при разработке систем «Поларис».

В странах СНГ (в том числе и в Казахстане) работы по сетевому планированию начались в 60-х годах ХХ столетия. Тогда методы СПУ нашли применение в строительстве и научных разработках. В дальнейшем сетевые методы стали широко применяться и в других областях народного хозяйства.

СПУ основано на моделировании процесса с помощью сетевого графика и представляет собой совокупность расчетных методов, организационных и контрольных мероприятий по планированию и управлению комплексом работ [1–5].

Система СПУ позволяет:

• формировать календарный план реализации некоторого комплекса работ;
• выявлять и мобилизовывать резервы времени, трудовые, материальные и денежные ресурсы;
• осуществлять управление комплексом работ по принципу «ведущего звена», с прогнозированием и предупреждением возможных срывов в ходе работ;
• повышать эффективность управления в целом при четком распределении ответственности между руководителями разных уровней и исполнителями работ.

Диапазон применения СПУ весьма широк: от задач, касающихся деятельности отдельных лиц, до проектов, в которых участвуют сотни организаций и десятки тысяч людей (например, разработка и создание крупного территориально-промышленного комплекса).

Под комплексом работ (комплексом операций или проектом) следует понимать всякую задачу, для выполнения которой необходимо осуществить достаточно большое количество разнообразных работ. Это может быть и строительство некоторого здания, корабля, самолета или любого другого сложного объекта, и разработка проекта этого сооружения, и даже процесс построения планов реализации проекта.

Для того чтобы составить план работ по осуществлению больших и сложных проектов, состоящих из тысяч отдельных исследований и операций, необходимо описать его с помощью некоторой математической модели. Таким средством описания проектов (комплексов) является сетевая модель. 

Некоторые методологические замечания

В основу метода СПУ положена теория графов. Являясь разделом математического анализа, она исследует взаимные связи и отношения между множествами и внутри них [6–8].

Граф — это множество элементов, попарно соединенных отрезками. Такое соединение определенным образом упорядочено и подчиняется закону, позволяющему установить соответствие между каждым элементом множества.

Граф обычно обозначается символом G (X, Г). Элементы множества X изображаются точками плоскости и называются вершинами. Пары точек, для которых установлено соответствие Г, соединяются линией, называемой ребром. Если пары вершин графа соединены направленными линиями (дугами), то такой граф называется направленным. Последовательность дуг, при которой конец каждой предыдущей дуги совпадает с началом следующей, называется путем, а путь, у которого начальная вершина совпадает с конечной, — контуром. Сетевые модели относятся к несимметричным графам, у которых пары смежных вершин соединены дугами только в одном направлении.

На основе применения теории графов в планировании создана стройная система планирования и управления (СПУ). Систему СПУ можно характеризовать как совокупность научно обоснованных принципов организации планирования и управления, использующих вычислительную технику.

Главным условием успешного применения метода СПУ в экономическом анализе является соблюдение системного подхода при решении задач планирования и управления.

Основы построения сетевых моделей (графиков)

Основой системы СПУ является сетевая модель (сетевой график). Вершина сетевого графика называется событием, а ориентированные дуги — работами. События и работа — это главные элементы сетевого графика.

Событие — это результат выполнения одной или нескольких работ. На сетевых графиках им соответствуют условные знаки — кружки, квадраты и другие геометрические фигуры.

Работа обозначает действие, для выполнения которого требуется затратить время и какие-либо ресурсы, т.е. реальные хозяйственные и технологические процессы. На графике работа фиксируется безразмерными стрелками. Кроме того, существуют работы, которые не требуют затрат времени или ресурсов. Они называются зависимостями, или фиктивными работами, и показывают, что какое-либо событие не может совершиться раньше другого любого события и на графике отмечено пунктирной стрелкой.

Событие свершается лишь тогда, когда заканчиваются все предшествующие ему работы. В связи с этим различают исходное, начальное, конечное, промежуточное и завершающее события.

При построении сетевых графиков следует соблюдать ряд правил. На графиках не должно   быть «тупиков», т.е. событий, из которых не выходит ни одна работа. Образование «тупика» свидетельствует о том, что вызвавшая его работа не нужна и ее необходимо аннулировать. В сетевых графиках не должно быть и событий, которым не предшествует ни одна работа. Исключение составляет исходное событие. Кроме того, при построении сетевых графиков нельзя допускать, чтобы два события были связаны между собой двумя или больше работами. Если бывает, что выполняются две или несколько работ одновременно, то необходимо ввести дополнительное событие.

Построенный с соблюдением указанных правил сетевой график называется сетевой моделью выполнения комплекса работ. Для правильного кодирования включенных в сетевую модель элементов их необходимо пронумеровать. Исходному событию присваивается номер 1. Затем нужно вычеркнуть все выходящие из него работы и на оставшейся части сети событию, в которое не входит ни одна работа, присвоить номер 2 и т.д. Если окажется, что два или более события не имеют входящих работ, то номера им присваиваются произвольно.

При составлении сложных моделей, например, сетевой модели повышения эффективности производства, предприятия, прибегают к составлению графика по частям. Первоначально составляют фокальные графики, а затем их «сшивают» в общий.

Порядок разработки сетевой модели обычно следующий:

1. Устанавливаются предварительный перечень, содержание и сроки выполнения работ, соответствующие всей разработке в целом или отдельным ее частям.
2. Подсчитываются необходимые производственные ресурсы для выполнения каждой работы.
3. Анализируется взаимосвязь между отдельными работами и составляются исходные данные для построения сетевой модели.
4. Строится сетевая модель разработки и определяются ее параметры.
5. Производится оптимизация модели и окончательное ее формирование.

Рис. 1. Сетевая модель 

Поскольку каждая работа заключена между двумя событиями, то она обозначается двумя цифрами — соответственно номером предшествующего и последующего событий. При нумеровании событий следует тщательно проверять, чтобы в сети не было повторения одних и тех же номеров. Событие не может произойти до тех пор, пока предшествующая работа не будет закончена. В свою очередь, работа не может быть начата, пока предшествующее событие не будет выполнено. Следовательно, образуется цепь: событие — работа — событие.

В случае параллельных работ, у которых предшествующее и последующее события одни и  те же, вводятся дополнительно событие и фиктивная работа, например, работа 9–10, которая на графике обозначается пунктирной линией.

При разработке больших сетевых графиков, когда, количество событий более 50, для упрощения анализа следует сети разделять на части. Каждая такая часть составляется отдельно, здесь четко указываются входные и выходные события, связанные с другими участками сети. При наличии общего сетевого графика такой участок может быть включен в модель укрупненно.

Время, необходимое на выполнение любой работы, на графике отмечается цифрой, проставляемой над данной работой. При составлении сетевого графика необходимо обеспечить в нем не только строгую последовательность и взаимосвязь работ, но и оценить каждую работу с точки зрения затрат времени на ее выполнение и обеспечение материальными и трудовыми ресурсами.

Любая непрерывная последовательность работ на сетевом графике называется путем. Путь от начального до завершающего события называется полным. В сетевом графике их может быть несколько. Например, на сетевом графике (рис. 1) имеется 6 полных путей, проходящих через следующие работы:

1 путь — 1–3, 3–4, 4–14, 14–15, 15–16, 16–17, 17–18, 18–19, 19–20, 20–21;

2 путь— 1–2, 2–5, 5–7, 7–13, 13–14, 14–15, 15–16, 16–17, 17–18, 18–19, 19–20, 20–21;

3 путь — 1–2, 2–5, 2–7, 7–8, 8–14, 14–15, 15–16, 16–17, 17–18, 18–19, 19–20, 20–21;

4 путь — 1–2, 2–6, 6–9, 9–10, 10–12, 12–17, 17–18, 18–19, 19–20, 20–21;

5 путь — 1–2, 2–6, 6–10, 10–11, 11–17, 17–18, 18–19, 19–20, 20–21;

6 путь — 1–2, 2–6, 6–12, 12–17, 17–18, 18–19, 19–20, 20–21.

Длина пути определяется суммой продолжительности каждой из составляющих его работ. Путь, продолжительность которого наибольшая, называется критическим. Это время выполнения всей программы работ. Зная дату начала работ и продолжительность критического пути, можно установить дату окончания работ по программе.

Таким образом, любое увеличение продолжительности работ, находящихся на критическом пути, задерживает выполнение всей программы работ, а уменьшение срока в целом приближает время окончания. В связи с этим особое внимание надо уделять работам, находящимся на критическом пути. Возможность выделения так называемых критических работ является важнейшим преимуществом, определяющим эффективность метода СПУ.

Зная время выполнения каждой работы, определяем продолжительность каждого из возможных путей сетевого графика, представленного на рисунке 1:

l1 — 1+1,5+3+3+3+3+3+2+1,2=20,7 ч;

l2 — 1+1+0,5+0,8+3+3+3+3+3+2+1,2=21,9 ч; l3 — 1+1+0,5+0,3+3+3+3+3+2+1,2=21 ч;

l4  — 1+1+2+3+3+3+2+1,2=16,2 ч; l5 — 1+1+2,5+3+3+3+2+1,2=16,7 ч; l6 — 1+1+5+3+3+2+1,2=16,2 ч.

Следовательно, в нашем примере самый длительный, т.е. критический путь, проходит через работы: 1–2, 2–5, 5–7, 7–13, 13–14, 14–15, 15–16, 16–17, 17–18, 18–19, 19–20, 20–21. Продолжитель-

ность его 21,9 ч. Это означает, что анализ производственной деятельности может быть закончен за 21,9 часа. При необходимости сокращения срока работ следует сократить продолжительность критического пути, но настолько, чтобы остальные пути не превышали по своей продолжительности критический.

Все остальные пути графика являются ненапряженными, имеют меньшую продолжительность и располагают резервами времени.

Кроме определения критического пути, в сетевом графике рассчитывают наиболее ранние и наиболее поздние сроки начала и окончания работ и резервы времени. Эти показатели характеризуют состояние работ в общей программе и показывают, какими резервами времени располагает та или иная работа.

Все работы, за исключением лежащих на критическом пути, имеют резервы времени. Определить их можно путем сравнения ранних и поздних сроков начала и окончания работы. Понятие «резервы времени» является важным при управлении работами с помощью сетевого графика. Зная резервы времени, можно решить вопрос, где и на каких работах лучше всего их использовать, как перераспределить силы бригады (рациональное их использование). Различают полный и свободный резервы времени.

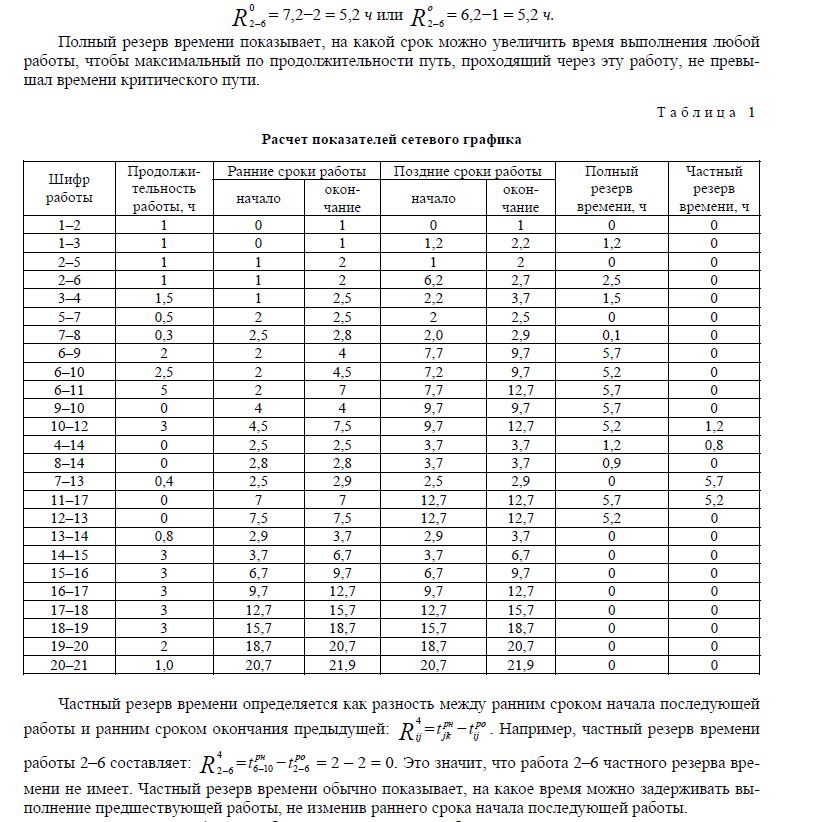
Полный резерв времени — это разность позднего и раннего сроков начала или окончания работы. Так, полный резерв времени работы 2–6 будет равен: 

Полный резерв времени показывает, на какой срок можно увеличить время выполнения любой работы, чтобы максимальный по продолжительности путь, проходящий через эту работу, не превышал времени критического пути. 

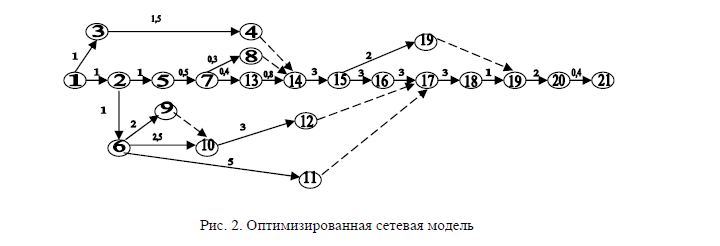
Расчет показателей сетевого графика

Т а б л и ц а  1

Расчет сетевого графика с небольшим количеством событий производится вручную. Результаты расчета записываются в таблицу 1, составленную по следующей форме.

Как видим, критический путь проходит через работы, у которых совпадают ранние и поздние сроки начала и окончания их. Таким образом, у работ, лежащих на критическом пути, резерв времени равен нулю. Отсутствие резерва является неотъемлемым свойством, присущим критическому пути.

После расчета показателей графика определяют дату раннего начала работ, и все работы привязывают к календарным датам. Рассмотренный табличный метод расчета сетевого графика вручную может применяться для анализа сетей с числом работ не выше 70–100.

Сетевые графики с большим количеством работ или более сложными логическими связями вручную рассчитывать сложно, требуют они больших затрат труда, времени и снижают эффективность сетевого планирования. В таких случаях необходимо применять вычислительную технику. Для этого составляется программа, исходными данными которой служат время выполнения работ, номера событий. Путем обсчета определяется критический путь, наиболее ранние и поздние сроки начала и окончания работ.

После окончания расчета сетевого графика сравнивают срок выполнения работ, равный длине критического пути, с установленным директивным сроком. Если они совпадают, то работу по составлению сетевой модели можно считать законченной.

Оптимизация сетевой модели

В случае, когда рассчитанный срок получается больше директивного, принимают меры для сокращения критического пути, т.е. производят оптимизацию сетевой модели по времени. Оптимизация графика может осуществляться по следующим двум направлениям.

1. Сокращают срок продолжительности выполнения работ, лежащих на критическом пути, за счет подключения дополнительных исполнителей с ненапряженных путей, имеющих резервы времени.
2. Совершенствуют построение сети. По ряду работ изменяют их логическую последовательность и взаимозависимость. Например, производят замену последовательно выполняемых работ на параллельные. Пересчет продолжительности выполнения работ, лежащих на критическом пути, с учетом наиболее рационального распределения ресурсов может производиться несколько раз, пока не будет достигнут желаемый результат.

В разбираемом случае сетевая модель имеет продолжительность  критического  пути, равную 21,9 ч. Директивный срок, в течение которого должен быть закончен анализ — 20 ч. Значит, сетевой график необходимо оптимизировать так, чтобы продолжительность критического пути не превышала 20 ч. 

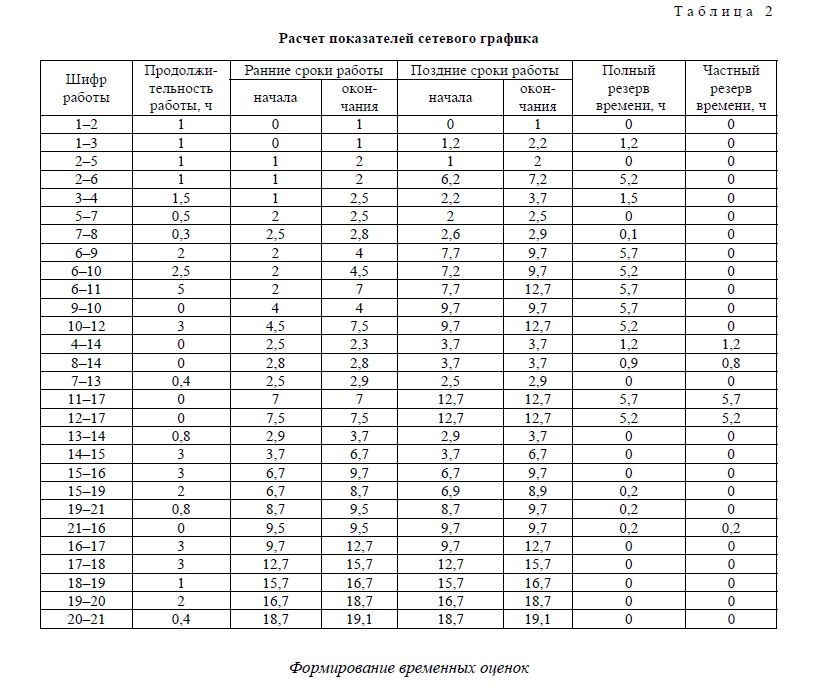
Рис. 2. Оптимизированная сетевая модель 

Директор вычислительного центра, возглавляющий работу по анализу, принимает решение: часть объема, предусмотренного работами 18–19 и 20–21, провести параллельно с выполнением работы 15–16, после чего производятся построение и расчет окончательного варианта сетевого графика.

На рисунке 2 изображен оптимизированный вариант сетевой модели сбора информации и анализа производственно-хозяйственной деятельности угольных предприятий.

Расчет ранних и поздних сроков начала и окончания работ, а также полного и частного резервов времени работ второго варианта сетевой модели произведен в таблице 2.

Выполненный расчет показывает, что критический путь второго варианта сетевого графика проходит через работы 1−2, 2−5, 5−7, 7−13, 13−14, 14−15, 15−16, 16−17, 17−18, 18−19, 19−20 и 20−21.

Продолжительность этого пути составляет 19,1 ч, что меньше установленного директивного срока. Следовательно, оптимизированный вариант сетевой модели может быть принят к исполнению.

При разработке программ иногда возникают новые обстоятельства и новые задачи. Такие ситуации легко вносятся в сетевую модель и учитываются ею, что обеспечивает динамичность планирования и управления, исходя из имеющихся ресурсов.

В случае, когда этих ресурсов недостаточно, с помощью сетевого графика на любом этапе работ можно убедительно обосновать необходимость выделения дополнительных ресурсов либо продления срока работ.

Расчет показателей сетевого графика

Т а б л и ц а  2

Формирование временных оценок

Каждая входящая в сетевую модель работа протекает во времени. Следовательно, она должна иметь временную оценку. Установление временных оценок планируемых работ при построении сетевых моделей является важным элементом, поскольку от этого во многом зависит качество плана и реальность выполнения всей программы работ.

Существуют три оценки продолжительности каждой работы — оптимистическая, вероятная и пессимистическая. Оптимистическая определяет время выполнения работы при условии, что никаких затруднений не будет; вероятная намечает продолжительность работы, при условии, что никаких неожиданных отклонений не произойдет и условия для выполнения работы будут простыми и легкими; пессимистическая определяет максимально потребное время, исходя из предположений, что работы будут осуществляться при неблагоприятных условиях.

Пользуясь тремя оценками потребного времени для каждой работы, рассчитывают ожидаемое время на выполнение работы по формуле

Оперативное управление и контроль включают действенный контроль за фактическим состоянием выполнения программы, выявление в ходе работ возникающих отклонений, анализ всех изменений и принятие соответствующих решений для их устранения. Главной задачей процесса управления и контроля является разработка таких мероприятий, которые позволили бы обеспечить сокращение длины критического пути и соответствие расчетных данных сети установленному директивному сроку.

Составленная и принятая к исполнению сетевая модель не может быть неизменной, так как в процессе работ изменяются оценки времени, уточняются отдельные операции, выявляется необходимость в дополнительных работах. Объем работ по уточнению и корректировке сети также зависит от того, насколько качественно был составлен исходный график.

Сущность стадии управления и контроля при сетевом планировании заключается в том, что благодаря систематической информации выявляются все возможные трудности и предусматриваются мероприятия по их устранению.

Периодический контроль и анализ состояния работ обеспечивают эффективность принимаемых решений и дают возможность оценить влияние расчетных показателей на ход выполнения программы.

Список литературы 

1. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Исследование операций в экономике: Учеб. пособие. — М.: Банки и биржи, ЮНИТИ, 1997. — 407 с.
2. Разумов И.М., Белова Л.Д., Ипатов М.И., Проскурякова А.В. Сетевые графики в планировании: Учеб. пособие. — М.: Высш. шк., 1981. — 168 с.
3. Большаков А.С. Моделирование в менеджменте: Учеб. пособие. — М.: Информационно-издат. дом «Филинъ», Рилант, 2000. — 464 с.
4. Кузнецов К.К., Рапопорт П.И. Сетевые методы планирования и управления в угольной промышленности. — М.: Недра, 1975. — 208 с.
5. Холод Н.И., Кузнецов А.В., Жихар Я.Н. и др. Экономико-математические методы и модели. — Минск: Изд-во БГЭУ, 1999. — 413 с.
6. Кристофидес Н. Теория графов: Алгоритмический подход: Пер. с англ. — М.: Мир, 1978. — 432 с.
7. Харари Ф. Теория графов: Пер. с англ. — М.: Мир, 1973. — 300 с.
8. Цой С., Цхай С.М. Прикладная теория графов. — Алма-Ата: Наука, 1971. — 500 с.

Системы сетевого планирования и управления (СПУ), являющиеся разновидностью автоматизированных систем управления, предназначены для управления деятельностью, направленной на достижение определенной цели.

Объектом управления в системах СПУ является коллектив, располагающий определенными ресурсами и выполняющий комплекс работ, призванный обеспечить достижение намеченной цели. Метод СПУ позволяет в любых, даже самых сложных ситуациях, быстро принимать наиболее правильные решения, выявить резервы времени и средств на одних участках работы и перебросить их на другие, более напряженные.

Важной особенностью систем СПУ является системный подход к вопросам организации управления, согласно которому коллективы исполнителей, принимающие участие в проекте и объединенные общностью поставленной перед ними задачи, несмотря на их различную ведомственную подчиненность, рассматриваются как звенья единой сложной организационной системы.

Для отображения процесса выполнения проекта и управления им в системах СПУ используется сетевая модель.

7.2.1.1. Сетевой график. Критический путь

Важнейшей основой метода СПУ является сетевой график.

Сетевой график представляет собой графическое изображение последовательности выполнения комплексной разработки, показывающее взаимосвязь и взаимозависимость отдельных этапов, выполнение которых обеспечивает достижение конечной цели разработки.

Достоинство сетевых графиков заключается в их наглядности и сравнительной простоте исполнения. Сетевые графики позволяют:

а) выявлять важнейшие работы, от своевременного выполнения которых зависит соблюдение сроков окончания всей разработки;

б) наглядно представлять ход разработки в целом, взаимосвязь и взаимозависимость отдельных этапов разработки;

в) определять общую потребность в рабочей силе и материальных ресурсах для выполнения плана;

г) выявлять резервы времени и материальные ресурсы с целью наиболее эффективного выполнения плана;

д) совершенствовать методы планирования и устанавливать строгий ритм в работе;

е) использовать вычислительную технику для расчета показателей сетевых графиков.

Приведенный перечень преимуществ применения методов сетевого планирования и управления не является исчерпывающим, однако дает возможность оценить его огромное мобилизующее значение как эффективного средства улучшения организации труда и управления производством.

Таким образом, методы СПУ, обеспечивая руководителя необходимой информацией о ходе выполнения разработки, дают ему возможность принимать решения, направленные на достижение максимального эффекта при минимальных затратах времени и ресурсов, поэтому применение методов СПУ близко подходит к возможности разработки оптимальных планов.

Рассмотрим теперь основные термины, применяемые при пользовании сетевыми графиками.

Работа характеризует конкретный этап трудового процесса по выполнению определенной операции комплексной разработки. Этот термин означает, что для осуществления работы требуются затраты рабочей силы, материальных ресурсов и времени.

Событие является фактом окончания всех предшествующих данному событию работ, либо началом работ, следующих непосредственно за данным событием. Для совершения события не требуется никаких затрат, а само событие не имеет продолжительности.

При составлении сетевого графика необходимо обеспечить логическую последовательность наступления событий, которая определяется взаимосвязью и последовательностью выполнения соответствующих работ. На сетевом графике события обозначаются кружками, в которые в определенной последовательности вписываются цифры.

<5> <17> <30>

Приведем следующий простейший график:

©-КЗ-КЭ-К!)

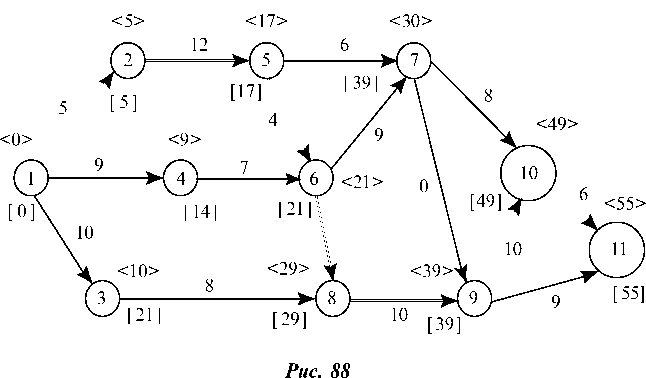
Из графика следует, что событие 3 не может наступить, пока не совершится событие 2 и т. д. При этом событие 2 называется последующим по отношению к событию 1, так же как событие 4 является последующим по отношению к событию 3. Событие 3 — предшествующее по отношению к событию 4. В указанных определениях имеется в виду, что события следуют одно за другим и между ними нет промежуточных событий. Одно событие может иметь и несколько предшествующих, либо последующих событий. Например, на графике (рис. 88) событие 6 имеет два предшествующих события (4 и 5).

Если наступлению данного события не предшествует какая-либо работа, то это событие называется исходным (на рис. 88 это событие 1). Событие, не имеющее последующих работ, называется завершающим, т. е. наступлением завершающего события достигается конечная цель данной разработки (на рис. 88 это событие 11).

Операция — это сама работа или действие. Она обозначается:

Это означает, что начальное событие г происходит раньше конечного события у, а длительность операции (г — у), которая обозначается стрелкой, будет равна ^-.

Фиктивной называется работа, не требующая затрат рабочего времени и ресурсов на ее выполнение. Она характеризует зависимость выполнения данной работы от выполнения какой-то другой. Длительность этой работы ^ = 0 (на рис. 88 это работа 7—9).

Продолжительность выполнения работы измеряется в единицах времени: часах, днях, неделях и т. д.

Любая последовательность работ в сети, в которой конечное событие каждой работы последовательности совпадает с начальным событием следующей за ней работы, называется путем.

Следует различать два вида пути:

1) полным путем называется непрерывная последовательность выполнения работ от исходного до завершающего события;

2) критическим путем называется путь от исходного до завершающего события, который характеризуется наибольшей продолжительностью выполнения работ, находящихся на этом пути.

Первичный сетевой график составляется на основе исходных (первичных) данных представленных ответственными исполнителями этапов комплексной работы до его оптимизации.

Рассмотрим детальнее сетевой график некоторого комплекса работ, который необходимо выполнить, чтобы организовать производство нового вида изделия (рис. 88).

В практическом применении сетевых графиков может быть различное количество событий и работ, характеризующих те или иные виды разработок. При этом, если количество событий не превышает 300, графики обсчитывают с помощью простейших микрокалькуляторов. При числе же событий свыше 300, и в особенности 500—1000 и более, параметры сети рассматриваются при помощи ЭВМ.

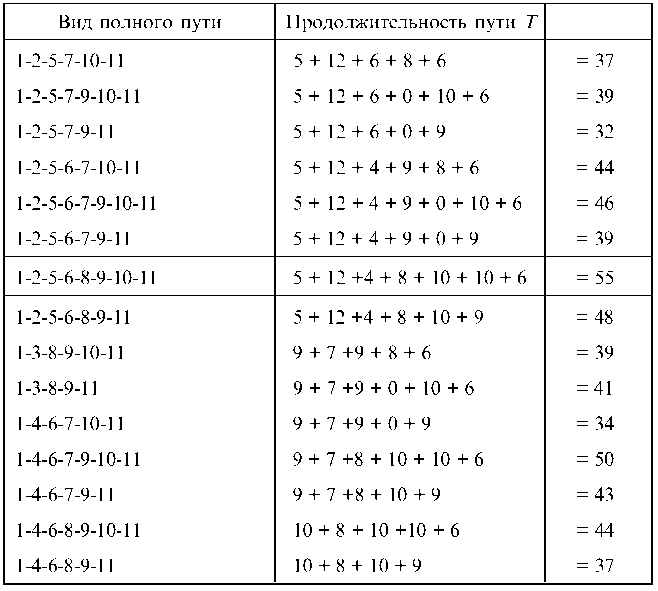
Определяем продолжительности полных путей, для чего составляем табл. 7.13.

Таблица 7.13

Отсюда видно, что продолжительность критического пути, т. е. пути, имеющего наибольшую продолжительность, равна Ткр = 55 (дней). Это означает, что при прочих равных условиях раньше чем через 55 (дней) данная работа не закончится. Следовательно, продолжительность критического пути представляет собой наиболее ранний срок завершения всей работы от исходного до завершающего события.

В сети может быть несколько критических путей.

7.2.1.2. Временные параметры сетей. Резервы времени

Основными временными параметрами сетей являются ранние и поздние сроки наступления событий. Зная их, можно вычислить остальные параметры сети — сроки начала и окончания работ и резервы времени событий и работ.

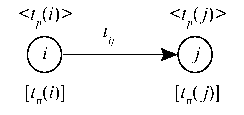
Рассмотрим работу (i — j):

Ранний возможный срок < tp (i) > наступления события j есть наименьший возможный срок окончания данной работы:

т. е. раннее возможное событие j равно раннему возможному предшествующему событию i, сложенному с длительностью работы (i — j).

Когда для события j имеется несколько ранних возможных, то берется наибольшее.

Очевидно, максимальное значение раннего окончания работы будет характеризовать продолжительность критического пути (Гкр)-

Поздним допустимым сроком наступления события называется максимально допустимый срок наступления этого события, не требующий увеличения времени на осуществление всего проекта.

Позднее допустимое равняется разности позднего окончания события j и продолжительности последующих работ.

Если для события i будет несколько поздних допустимых, то берется наименьшее.

Работы, у которых < tp (j) > и [t„ (i)] совпадают, называются критическими работами, лежащими на критическом пути. Это есть второй способ определения критического пути.

Как уже отмечалось, продолжительность критического пути больше продолжительности любого другого пути сетевого графика.

Разность между продолжительностью критического пути Ткр и продолжительностью пути L — T (L) называется резервом времени пути L.

Резерв времени R (L) показывает, на сколько могут в сумме быть увеличены продолжительности работ, принадлежащих пути L, без влияния на срок проекта.

Различают четыре резерва времени:

1. Полный резерв ПР = Rn (i; j) = tn (j) — tp (i) — j (7.16)

2. Свободный резерв CP = Rc (i; j) = tp (j) — tp (i) — tij, (7.17)

3. Независимый резерв ЯР = Rh (i; j) = tp (/) — tn (i) — tj, (7.18)

4. Гарантированный резерв ГР = Rr (i; j) = ^ (j) — tn (i) — ty, (7.19)

Полный резерв времени — это количество времени, на которое можно перенести начало работ или увеличить продолжительность без изменения общего срока проекта.

Из этого определения следует, что полный резерв времени по отдельным работам позволяет маневрировать ресурсами с тем, чтобы наилучшим образом выполнить всю разработку. Полный резерв времени является зависимым резервом, т. е. его применение может привести к изменению резервов по другим работам. Поэтому при использовании полного резерва времени обычно пересчитывают параметры сетевого графика для определения нового распределения резервов.

Свободный резерв времени — это количество времени, на которое можно перенести начало работ или увеличить их продолжительность без изменения раннего начала последующих работ, этот резерв может быть использован непосредственно исполнителем той или иной работы, и это не повлечет за собой изменения условий производства последующих работ. Полный же резерв времени может быть использован только с разрешения центра, так как его использование изменяет ранние сроки начала последующих работ.

Всегда ПР > CP.

На критическом пути все резервы времени равны нулю.

Это свойство может служить третьим определением критического пути.

Независимый резерв времени означает запас времени, который имеет исполнитель, когда предшествующие работы заканчиваются в неудобные для него сроки, а он заканчивает свою работу в ранний срок, не расходуя резервов следующих за ним работ.

Гарантированный резерв означает для исполнителя работы резерв времени, который он имеет, когда исполнители предшествующих работ заканчивают их в неудобные для него поздние допустимые сроки, но и он сдает свою работу в поздний срок.

Если (г; у) и Ян (г; у) имеют отрицательные значения, то эти резервы заменяются нулем.

Существуют различные формы расчета параметров сети: табличный и графический. Наиболее удобной является табличная форма.

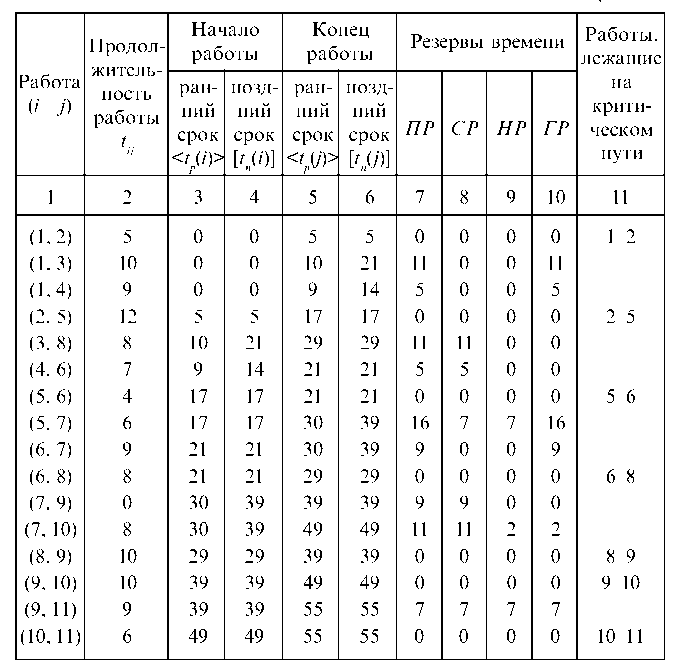
Для рассмотренного примера сетевого графика (рис. 88) в табл. 7.14 приведены ранние и поздние сроки окончания и начала работ и резервы времени.

При анализе графика прежде всего обращают внимание на критические работы, от которых в решающей степени зависит своевременное и качественное выполнение всей разработки. Следует также обращать внимание на наличие резервов времени по отдельным работам. Например, по работе (5, 7) свободный резерв составляет 7 дней. Это означает, что продолжительность выполнения данной работы при необходимости можно «растянуть» в пределах семи дней, либо начать эту работу позже.

Нахождение величины резервов нельзя рассматривать, однако, как оценку времени простоя исполнителей. На выполнение работ сетевого графика при правильном планировании выделяются ресурсы (в человеко-часах, машино-часах и т. д.), равные суммарной трудоемкости всех предусмотренных работ.

Оценка резервов времени позволяет более рационально распределить трудовые и материальные ресурсы по работам графика. Большинство работ обладает закономерностью: увеличивая число исполнителей, удается уменьшить длительность выполнения работы. Эта закономерность может иметь разные формы, но

чаще других встречается гиперболическая зависимость г = а + — длительности работы г от количества работников х.

Перебрасывая людей и технику с ненапряженных работ на напряженные работы критического пути, можно сократить сроки выполнения всего комплекса работ.

Одним из важнейших преимуществ применения сетевых графиков является возможность их оптимизации по различным признакам: по времени (сокращение Гкр), по людским ресурсам, по материальным ресурсам, по стоимости и технико-экономическим показателям, а также по различным сочетаниям этих признаков.

Так, например, оптимизация сетевого графика по времени предполагает, прежде всего, нахождение возможности сокращения продолжительности критического пути. Это может быть достигнуто различными путями.

Из сетевого графика видно, что сокращение общей продолжительности выполнения разработки возможно только за счет сокращения продолжительности выполнения работ, лежащих на критическом пути.

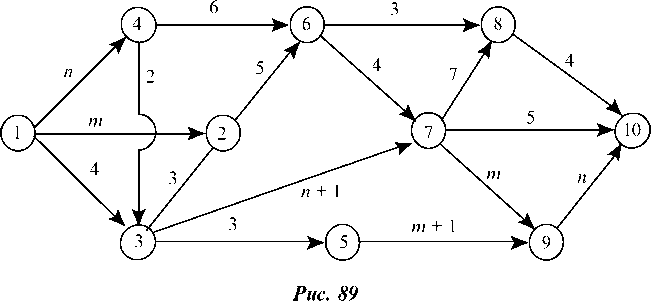
7.2.1.3. Пример построения сетевого графика задачи 15.1 контрольной работы (рис. 89).