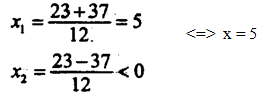-
- 0
-
А) При одновременной работе двух насосов пруд был очищен за
2 ч 55 мин. За сколько времени мог бы очистить пруд каждый
насос, работая отдельно, если один из них может эту работу
выполнить на 2 ч быстрее другого?
б) Два экскаватора, работая одновременно, выполняют
некоторый объем земляных работ за 3 ч 45 мин. Один
экскаватор, работая отдельно, может выполнить этот объем
работ на 4 ч быстрее, чем другой. Сколько времени требуется
каждому экскаватору в отдельности для выполнения того же
объема земляных работ?
Даю 20 баллов
-
Комментариев (0)
-
- 0
-
А)Возьмём за 1 весь объём работы., а за Х-время, за которое первый насос смог бы очистить пруд, если бы работал один, тогда время второго насоса будет (Х+2). За 1 час первый насос выполняет 1/Х часть работы, а второй насос 1/(Х+2), а работая вместе они за час выполняют (1/Х+1/9Х+2)) часть работы. Зная, что вместе они очистили пруд за 2ч55 мин (2ч55 мин=2 11/12 часа), составляем уравнение:
(1/Х+1/(Х+2))*2 11/12=1
1/Х+1/(Х+2)=12/35
35*(Х+2)+35*Х=12*Х*(Х+2)
35*Х+70+35*Х=12*Х в квадрате+24*Х
12*Х в квадрате-46*Х-70=0
Дискриминант равен 5476, а корень из дискриминанта=74.
Х1=5
Х2 не находим, так как это отрицательное число.
Значит первый насос мог бы очистить пруд за 5 часов, а второй насос за 5+2=7 часов.
можно немного по другому.просто брат такую задачу решал
х — время 1-го насоса
х+2 — время 2-го насоса
1/х — производительность 1-го насоса
1/(х+2) — производительность 2-го насоса
2 часа 55 минут = 35/12 часа
Уравнение
1/х + 1/(х+2) = 1 / (35/12)
Умножаем все члены на 35х*(х+2)
35*(х+2) + 35х = 12х*(x+2)
35x + 70 + 35x = 12x^2 + 24x
12x^2 — 46x — 70 = 0
6x^2 — 23x — 35
х1 = 5
х2 = -7/6 (не удовлетворяет условию)
х + 2 = 5 + 2 = 7
Ответ:за 5 и за 7 часов
-
Комментариев (0)
Ваш ответ
Возьмём за 1 весь объём работы., а за Х-время, за которое 1-ый насос сумел бы очистить пруд, если бы работал один, тогда время второго насоса будет (Х+2). За 1 час 1-ый насос исполняет 1/Х часть работы, а второй насос 1/(Х+2), а работая вместе они за час выполняют (1/Х+1/9Х+2)) часть работы. Зная, что вместе они очистили пруд за 2ч55 мин (2ч55 мин=2 11/12 часа), сочиняем уравнение:
(1/Х+1/(Х+2))*2 11/12=1
1/Х+1/(Х+2)=12/35
35*(Х+2)+35*Х=12*Х*(Х+2)
35*Х+70+35*Х=12*Х в квадрате+24*Х
12*Х в квадрате-46*Х-70=0
Дискриминант равен 5476, а корень из дискриминанта=74.
Х1=5
Х2 не находим, так как это отрицательное число.
Значит 1-ый насос мог бы очистить пруд за 5 часов, а 2-ой насос за 5+2=7 часов.
можно немножко по другому.просто брат такую задачку решал
х — время 1-го насоса
х+2 — время 2-го насоса
1/х — производительность 1-го насоса
1/(х+2) — производительность 2-го насоса
2 часа 55 минут = 35/12 часа
Уравнение
1/х + 1/(х+2) = 1 / (35/12)
Умножаем все члены на 35х*(х+2)
35*(х+2) + 35х = 12х*(x+2)
35x + 70 + 35x = 12x^2 + 24x
12x^2 — 46x — 70 = 0
6x^2 — 23x — 35
х1 = 5
х2 = -7/6 (не удовлетворяет условию)
х + 2 = 5 + 2 = 7
Ответ:за 5 и за 7 часов
Светило науки — 707 ответов — 45085 раз оказано помощи
Возьмём за 1 весь объём работы., а за Х-время, за которое первый насос смог бы очистить пруд, если бы работал один, тогда время второго насоса будет (Х+2). За 1 час первый насос выполняет 1/Х часть работы, а второй насос 1/(Х+2), а работая вместе они за час выполняют (1/Х+1/9Х+2)) часть работы. Зная, что вместе они очистили пруд за 2ч55 мин (2ч55 мин=2 11/12 часа), составляем уравнение:
(1/Х+1/(Х+2))*2 11/12=1
1/Х+1/(Х+2)=12/35
35*(Х+2)+35*Х=12*Х*(Х+2)
35*Х+70+35*Х=12*Х в квадрате+24*Х
12*Х в квадрате-46*Х-70=0
Дискриминант равен 5476, а корень из дискриминанта=74.
Х1=5
Х2 не находим, так как это отрицательное число.
Значит первый насос мог бы очистить пруд за 5 часов, а второй насос за 5+2=7 часов.
можно немного по другому.просто брат такую задачу решал
х — время 1-го насоса
х+2 — время 2-го насоса
1/х — производительность 1-го насоса
1/(х+2) — производительность 2-го насоса
2 часа 55 минут = 35/12 часа
Уравнение
1/х + 1/(х+2) = 1 / (35/12)
Умножаем все члены на 35х*(х+2)
35*(х+2) + 35х = 12х*(x+2)
35x + 70 + 35x = 12x^2 + 24x
12x^2 — 46x — 70 = 0
6x^2 — 23x — 35
х1 = 5
х2 = -7/6 (не удовлетворяет условию)
х + 2 = 5 + 2 = 7
Ответ:за 5 и за 7 часов
Возьмём за 1 весь объём работы., а за Х-время, за которое первый насос смог бы очистить пруд, если бы работал один, тогда время второго насоса будет (Х+2). За 1 час первый насос выполняет 1/Х часть работы, а второй насос 1/(Х+2), а работая вместе они за час выполняют (1/Х+1/9Х+2)) часть работы. Зная, что вместе они очистили пруд за 2ч55 мин (2ч55 мин=2 11/12 часа), составляем уравнение:
(1/Х+1/(Х+2))*2 11/12=1
1/Х+1/(Х+2)=12/35
35*(Х+2)+35*Х=12*Х*(Х+2)
35*Х+70+35*Х=12*Х в квадрате+24*Х
12*Х в квадрате-46*Х-70=0
Дискриминант равен 5476, а корень из дискриминанта=74.
Х1=5
Х2 не находим, так как это отрицательное число.
Значит первый насос мог бы очистить пруд за 5 часов, а второй насос за 5+2=7 часов.
можно немного по другому.просто брат такую задачу решал
х — время 1-го насоса
х+2 — время 2-го насоса
1/х — производительность 1-го насоса
1/(х+2) — производительность 2-го насоса
2 часа 55 минут = 35/12 часа
Уравнение
1/х + 1/(х+2) = 1 / (35/12)
Умножаем все члены на 35х*(х+2)
35*(х+2) + 35х = 12х*(x+2)
35x + 70 + 35x = 12x^2 + 24x
12x^2 — 46x — 70 = 0
6x^2 — 23x — 35
х1 = 5
х2 = -7/6 (не удовлетворяет условию)
х + 2 = 5 + 2 = 7
Ответ:за 5 и за 7 часов
Возьмём за 1 весь объём работы., а за Х-время, за которое первый насос смог бы очистить пруд, если бы работал один, тогда время второго насоса будет (Х+2). За 1 час первый насос выполняет 1/Х часть работы, а второй насос 1/(Х+2), а работая вместе они за час выполняют (1/Х+1/9Х+2)) часть работы. Зная, что вместе они очистили пруд за 2ч55 мин (2ч55 мин=2 11/12 часа), составляем уравнение:
(1/Х+1/(Х+2))*2 11/12=1
1/Х+1/(Х+2)=12/35
35*(Х+2)+35*Х=12*Х*(Х+2)
35*Х+70+35*Х=12*Х в квадрате+24*Х
12*Х в квадрате-46*Х-70=0
Дискриминант равен 5476, а корень из дискриминанта=74.
Х1=5
Х2 не находим, так как это отрицательное число.
Значит первый насос мог бы очистить пруд за 5 часов, а второй насос за 5+2=7 часов.
можно немного по другому.просто брат такую задачу решал
х — время 1-го насоса
х+2 — время 2-го насоса
1/х — производительность 1-го насоса
1/(х+2) — производительность 2-го насоса
2 часа 55 минут = 35/12 часа
Уравнение
1/х + 1/(х+2) = 1 / (35/12)
Умножаем все члены на 35х*(х+2)
35*(х+2) + 35х = 12х*(x+2)
35x + 70 + 35x = 12x^2 + 24x
12x^2 — 46x — 70 = 0
6x^2 — 23x — 35
х1 = 5
х2 = -7/6 (не удовлетворяет условию)
х + 2 = 5 + 2 = 7
Ответ:за 5 и за 7 часов
Привет, полазил в интернте, и смотри что нашел:
Пусть первый насос выполняет работу за х ч, а второй — за х + 2 ч. Примем всю работу за единицу, тогда производительность первого , второго
,
Работая вместе 2 ч 55 мин, они выполнят всю работу:
<=> 70х + 70=12х2 + 24х <=> 12х2-46х-70 = 0 <=> 6х2 — 23х — 35 = 0
D = 529 + 840= 1369
Следовательно, первый насос мог бы очистить пруд за 5 ч, а второй —
за 7 ч. Ответ: 5 ч, 7 ч.
Задания
Версия для печати и копирования в MS Word
Тип 22 № 3939
При одновременной работе двух насосов пруд был очищен за 2 ч 55 мин. За сколько времени очистит пруд первый насос, работая один, если может выполнить эту работу на 2 ч быстрее второго насоса?
Спрятать решение
Решение.
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| 0 | |
| 1 | |
| 2 | |
| Максимальный балл | 2 |
Спрятать решение
·
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023