Контрольная работа по алгебре 9 класс «Арифметическая прогрессия». В работе 5 заданий на два варианта.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Проверочная работа по теме «Арифметическая прогрессия»»
Вариант №1. КР_Арифметическая прогрессия 9 кл
-
Найдите 10-й член арифметической прогрессии (аn), первый член которой 3, а разность равна 2.
-
Найдите сумму первых двадцати шести членов арифметической прогрессии (сп): 7; 11; … .
-
Последовательность задана формулой аn=5п +2 . Найдите сумму первых 10 членов последовательности.
-
Найдите разность, первый член и сумму первых 11 членов арифметической прогрессии (аn), если а6= 10 и а9 = 19.
-
Последовательность задана формулой аn=п2 +2. Найдите а3, а10 члены последовательности.
Вариант №2. КР_Арифметическая прогрессия 9 кл
-
Первый член арифметической прогрессии (ап) равен 3, а разность равна -3. Найдите 12-й член этой прогрессии.
-
Найдите сумму первых восемнадцати членов арифметической прогрессии (bп): 9; 7; … .
-
Последовательность задана формулой аn=3п -2 . Найдите сумму первых 8 членов последовательности.
-
Найдите разность и первый член и сумму первых 11 членов арифметической прогрессии (ап),если а6 =2 и а9 = 5.
№5 Последовательность задана формулой аn=п2-3. Найдите а4, а10 члены последовательности.
Вариант №1. КР_Арифметическая прогрессия 9 кл
-
Найдите 10-й член арифметической прогрессии (аn), первый член которой 3, а разность равна 2.
-
Найдите сумму первых двадцати шести членов арифметической прогрессии (сп): 7; 11; … .
-
Последовательность задана формулой аn=5п +2 . Найдите сумму первых 10 членов последовательности.
-
Найдите разность, первый член и сумму первых 11 членов арифметической прогрессии (аn), если а6= 10 и а9 = 19.
-
Последовательность задана формулой аn=5п +2. Найдите а3, а10 члены последовательности.
Вариант №2. КР_Арифметическая прогрессия 9 кл
-
Первый член арифметической прогрессии (ап) равен 3, а разность равна -3. Найдите 12-й член этой прогрессии.
-
Найдите сумму первых восемнадцати членов арифметической прогрессии (bп): 9; 7; … .
-
Последовательность задана формулой аn=3п -2 . Найдите сумму первых 8 членов последовательности.
-
Найдите разность и первый член и сумму первых 11 членов арифметической прогрессии (ап),если а6 =2 и а9 = 5.
-
Последовательность задана формулой аn=п2-3. Найдите а4, а10 члены последовательности.
Вариант №1. КР_Арифметическая прогрессия 9 кл
-
Найдите 10-й член арифметической прогрессии (аn), первый член которой 3, а разность равна 2.
-
Найдите сумму первых двадцати шести членов арифметической прогрессии (сп): 7; 11; … .
-
Последовательность задана формулой аn=5п +2 . Найдите сумму первых 10 членов последовательности.
-
Найдите разность, первый член и сумму первых 11 членов арифметической прогрессии (аn), если а6= 10 и а9 = 19.
-
Последовательность задана формулой аn=5п +2. Найдите а3, а10 члены последовательности.
Вариант №2. КР_Арифметическая прогрессия 9 кл
-
Первый член арифметической прогрессии (ап) равен 3, а разность равна -3. Найдите 12-й член этой прогрессии.
-
Найдите сумму первых восемнадцати членов арифметической прогрессии (bп): 9; 7; … .
-
Последовательность задана формулой аn=3п -2 . Найдите сумму первых 8 членов последовательности.
-
Найдите разность и первый член и сумму первых 11 членов арифметической прогрессии (ап),если а6 =2 и а9 = 5.
-
Последовательность задана формулой аn=п2-3. Найдите а4, а10 члены последовательности.
Проверочная работа по алгебре для 9 класса
Тема: Арифметическая прогрессия.
Подготовила Кривошеева Светлана Александровна
учитель математики МБОУСОШ №40 города Тулы
Инструкция к выполнению.
Задания подобраны так, что ответ предыдущего является условием следующего (математическая эстафета).
Задания для первого варианта:
№1. Выпишите первые пять членов арифметической прогрессии (аn): 6;3…
№2. В арифметической прогрессии (сn) первый член равен (а5) из задания №1, d=5. Найдите сумму первых двадцати членов этой прогрессии.
№3. Найдите номер члена арифметической прогрессии (bn), если b1=20, d=10, а bn=S20 из задания №2.
№4. Найти сумму всех натуральных чисел, не превосходящих n, где n-номер члена из задания №3.
№5. В арифметической прогрессии (хn) первый член равен сумме из задания №4, а равность равна- 25. Для каких членов прогрессии выполняется условие хn
№6.Последовательность задана формулой y=5n-2. Найдите сумму n-первых членов этой последовательности, если n-номер наименьшего положительного члена арифметической последовательности из задания №5.
№7. Сумма первых ста членов арифметической прогрессии равна сумме арифметической прогрессии из задания №6. Найдите сумму первых ста членов такой арифметической прогрессии, каждый член которой на 3 больше соответствующего члена данной прогрессии.
Решение заданий первого варианта:
№1.
(an): 6;3;…, значит d=3-6=-3. Ответ: 6;3;0;-3;-6;-9;-12;… а5=-6
№2.
(сn)-арифметическая прогрессия, с1=а5=-6, d=5.
Sn=0,5n(2a1+d(n-1)), S20=830.
№3.
(bn)-арифметическая прогрессия, (b1)=20, d=10,bn=S20=830.
bn=b1+d(n-1), 20+10(n-1)=830,n=82.
№4.
bn=n, n
№5.
x1=3403, d=-25, xn
xn=x1+d(n-1), 3403-25(n-1
№6.
yn=5n-2, n=137.Последовательность (уn)-арифметическая прогрессия, т. к. d=уn+1:уn=5.
y1=3, Sn=0,5n(2y1+d(n-1)),S137=46991.
№7
1.(an)-арифметическая прогрессия, S100=46991
(an): a1;a2;a;… S100=0,5(2a1+99d)100=(2a1+99)50=46991
2.(bn)- арифметическая прогрессия,
(bn): b1=a1+3; b2=a2+3;b3=a3+3;… S100=0,5(2b1+99d)100=
=(2(a1+3)+99d)50=((2a1+99d)+6)50=S100+300=46991+300=
=47291
Конечный результат для первого варианта 47291.
Задания для второго варианта:
№1.Выпишите первые пять членов арифметической прогрессии 10;5;…
№2.В арифметической прогрессии(cn) первый член равен a5 из задания №1, d=5.Найдите сумму первых двадцати первых членов прогрессии.
№3.Найдите номер члена арифметической прогрессии(bn), если b1=20,d=10,а b4=S20 из задания №2.
№4. Найдите сумму всех натуральных чисел, не превосходящих n,где n-номер члена из задания №3.
№5. В арифметической прогрессии (xn) первый член равен сумме из задания №4, а d=-25. Для каких членов прогрессии выполняется условие xn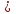
№6. Последовательность задана формулой yn=5n-2. Найдите сумму n-первых членов этой последовательности, если n –номер наименьшего положительного члена из задания №5.
№7. Сумма первых ста членов арифметической прогрессии равна сумме полученной в задании №6. Найдите сумму первых ста членов такой арифметической прогрессии, каждый член которой на 4 больше соответствующего члена данной прогрессии.
Решение заданий второго варианта:
№1. (an)-арифметическая прогрессия.
(an):10;5;… d=5-10=-5. Ответ: 10;5;0;-5;-10;…
№2.(cn)-арифметическая прогрессия, с1=-10, d=5.
Sn=0,5n(2c1+d(n-1)), n=20,S20=750.
№3. (bn)-арифметическая прогрессия,b1=20,d=10, bn=S20=750
bn=b1+d(n-1), 20+10(n-1)=750, n=74.
№4.(an)=n, n
Sn=0,5n(2a1+d(n-1)),S74=2775.
№5.(xn)-арифметическая прогрессия, x1=2775, d=-25, xn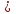
xn=x1+d(n-1), 2775-25(n-1)
№6. Последовательность (уn)-арифметическая прогрессия, т. к. d=уn+1:уn=5.
y1=3, Sn=0,5n(2y1+d(n-1)),S111=30858.
№7. 1.(an)-арифметическая прогрессия, S100=30858
(an): a1;a2;a;… S100=0,5(2a1+99d)100=(2a1+99)50=30858
2.(bn)- арифметическая прогрессия,
(bn): b1=a1+4; b2=a2+4;b3=a3+4;… S100=0,5(2b1+99d)100=
=(2(a1+4)+99d)50=((2a1+99d)+8)50=S100+400=30858+400=
=31258.
Конечный результат для второго варианта 31258.
Дидактические
материалы
Дидактические материалы содержат контрольную
работу для 9 класса по теме «Арифметическая прогрессия». Работа состоит из 30
равноценных вариантов одинакового уровня сложности и предназначена для
девятиклассников, изучающих математику на базовом уровне. Контрольная работа
рассчитана на один урок. К каждому варианту приводятся ответы.
|
А-9, 10. Найдите 23-й член 20. Найдите сумму 16 первых членов 30. Найдите сумму 60 первых членов 4. Является ли число 54,5 членом 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 18-й член 20. Найдите сумму 20 первых членов 30. Найдите сумму 40 первых членов 4. Является ли число 30,4 членом 5. Найдите сумму всех натуральных |
|
А-9, 10. Найдите 15-й член 20. Найдите сумму 22 первых членов 30. Найдите сумму 30 первых членов 4. Является ли число 20,3 членом 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 84-й член 20. Найдите сумму 10 первых членов 30. Найдите сумму 30 первых членов 4. Является ли число 30 членом 5. Найдите сумму всех натуральных |
|
А-9, 10. Найдите 31-й член 20. Найдите сумму 16 первых членов 30. Найдите сумму 20 первых членов 4. Является ли число 132 членом 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 65-й член 20. Найдите сумму 48 первых членов 30. Найдите сумму 10 первых членов 4. Является ли число 35 членом 5. Найдите сумму всех натуральных |
|
А-9, 10. Найдите 56-й член 20. Найдите сумму 30 первых членов 30. Найдите сумму 40 первых членов 4. Является ли число 106 членом 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 45-й член 20. Найдите сумму 25 первых членов 30. Найдите сумму 100 первых членов 4. Является ли число -1,3 членом 5. Найдите сумму всех натуральных |
|
А-9, 10. Найдите 26-й член 20. Найдите сумму 40 первых членов 30. Найдите сумму 50 первых членов 4. Является ли число -3,3 членом 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 8-й член арифметической 20. Найдите сумму 15 первых членов 30. Найдите сумму 50 первых членов 4. Является ли число -1 членом 5. Найдите сумму всех натуральных |
|
А-9, 10. Найдите 10-й член 20. Найдите сумму 20 первых членов 30. Найдите сумму 100 первых членов 4. Является ли число 3 членом 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 39-й член 20. Найдите сумму 18 первых членов 30. Найдите сумму 12 первых членов 4. Является ли число 128 членом 5. Найдите сумму всех натуральных |
|
А-9, 10. Найдите 26-й член 20. Найдите сумму 30 первых членов 30. Найдите сумму 20 первых членов 4. Является ли число 35 членом 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 37-й член 20. Найдите сумму 8 первых членов 30. Найдите сумму 15 первых членов 4. Является ли число 22 членом 5. Найдите сумму всех натуральных |
|
А-9, 10. Найдите 16-й член 20. Найдите сумму 8 первых членов 30. Найдите сумму 8 первых членов 4. Является ли число -51 членом а1 = 5 и a9 = 61? 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 27-й член 20. Найдите сумму 60 первых членов 30. Найдите сумму 12 первых членов 4. Является ли число 56 членом 5. Найдите сумму всех натуральных |
|
А-9, 10. Найдите 12-й член 20. Найдите сумму 9 первых членов 30. Найдите сумму 6 первых членов 4. Является ли число 10 членом а1 = 7 и a9 =23? 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 22-й член 20. Найдите сумму 9 первых членов 30. Найдите сумму 12 первых членов 4. Является ли число 181 членом 5. Найдите сумму всех натуральных |
|
А-9, 10. Найдите 5-й член арифметической 20. Найдите сумму 10 первых членов 30. Найдите сумму 30 первых членов 4. Является ли число 22 членом а1 = 7 и a6 =17? 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 11-й член 20. Найдите сумму 10 первых членов 30. Найдите сумму 6 первых членов 4. Является ли число 12 членом 5. Найдите сумму всех натуральных |
|
А-9, 10. Найдите 3-й член арифметической 20. Найдите сумму 8 первых членов 30. Найдите сумму 12 первых членов 4. Является ли число 19 членом а1 = 5 и a15 = 103? 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 9-й член арифметической 20. Найдите сумму 12 первых членов 30. Найдите сумму 10 первых членов 4. Является ли число 224 членом 5. Найдите сумму всех натуральных |
|
А-9, 10. Найдите 13-й член 20. Найдите сумму 8 первых членов 30. Найдите сумму 18 первых членов 4. Является ли число -4 членом а1 = 7 и a15 = 35? 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 3-й член арифметической 20. Найдите сумму 10 первых членов 30. Найдите сумму 6 первых членов 4. Является ли число 70 членом 5. Найдите сумму всех натуральных |
|
А-9, 10. Найдите 4-й член арифметической 20. Найдите сумму 12 первых членов 30. Найдите сумму 10 первых членов 4. Является ли число 25 членом а1 = 7 и a15 = 35? 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 16-й член арифметической 20. Найдите сумму 10 первых членов 30. Найдите сумму 8 первых членов 4. Является ли число -64 членом 5. Найдите сумму всех натуральных |
|
А-9, 10. Найдите 6-й член арифметической 20. Найдите сумму 8 первых членов 30. Найдите сумму 12 первых членов 4. Является ли число 112 членом а1 = 29 и a8 = 316? 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 82-й член 20. Найдите сумму 16 первых членов 30. Найдите сумму 8 первых членов 4. Является ли число 191 членом 5. Найдите сумму всех натуральных |
|
А-9, 10. Найдите 232-й член 20. Найдите сумму 6 первых членов 30. Найдите сумму 30 первых членов 4. Является ли число -51 членом а1 = 7 и a6 = 17? 5. Найдите сумму всех натуральных |
А-9, 10. Найдите 15-й член 20. Найдите сумму 6 первых членов 30. Найдите сумму 30 первых членов 4. Является ли число 56 членом 5. Найдите сумму всех натуральных |
ОТВЕТЫ.
|
Ответы: 10. a23 = 51 20. S16 = -352 30. S60 = 5430 4. n 5. S33 = 1683 |
Ответы: 10. a18 = 19 20. S20 = 150 30. S40 = 3200 4. n 5. S21 = 1617 |
|
Ответы: 10. x15 = 20. S22 = 30. S30 = 4. n 5. S75 = 11400 |
Ответы: 10. z84 = 20. S10 = 30. S30 = 1020 4. n 5. S20 = 1050 |
|
Ответы: 10. b31 = 19,2 20. S16 = -80 30. S20 = 480 4. n = 26, n 5. S40 = 4100 |
Ответы: 10. x65 = 20. S48 = 30. S10 = 4. n 5. S18 = 1197 |
|
Ответы: 10. y56 = 83,7 20. S30 = 1560 30. S40 = 1760 4. n = 25, n 5. S80 = 16200 |
Ответы: 10. c45 = 20. S25 = 30. S100 = 4. n 5. S50 = 6375 |
|
Ответы: 10. a26 = 7,6 20. S40 = 2240 30. S50 = 2700 4. n = 11, n 5. S70 = 12425 |
Ответы: 10. a8 = 36 20. S15 = 331,5 30. S50 = 5200 4. n 5. S50 = 3825 |
|
Ответы: 10. a10 = 37 20. S20 = 485 30. S100 = 20400 4. n = 5. S60 = 9150 |
Ответы: 10. u39 = -10,1 20. S18 = -315 30. S12 = -120 4. n 5. S30 = 2325 |
|
Ответы: 10. c26 = 20. S30 = 30. S20 = 4. n 5. S25 = 1300 |
Ответы: 10. x37 = 20. S8 = 30. S15 = 4. n 5. S13 = 455 |
|
Ответы: 10. a16 = -0,5 20. S8 = -15,2 30. S8 = 204 4. n = -7, n 5. S14 = 525 |
Ответы: 10. a27 = 2,4 20. S60 = 5490 30. S12 = 288 4. n = 5. S16 = 680 |
|
Ответы: 10. a12 = 4,7 20. S9 = 63 30. S6 = 72 4. n = 2,5, n 5. S17 = 765 |
Ответы: 10. a22 = -25,7 20. S9 = 86,4 30. S12 = -600 4. n = 61, n 5. S50 = 5100 |
|
Ответы: 10. a5 = -4 20. S10 = 75 30. S30 = 1080 4. n 5. S22 = 1012 |
Ответы: 10. a11 = 141 20. S10 = 75 30. S6 = 1386 4. n = 3,5, n 5. S37 = 2109 |
|
Ответы: 10. a3 = 29 20. S8 = 20 30. S12 = -2100 4. n = 3, n 5. S25 = 1950 |
Ответы: 10. х9 = -20 20. S12 = 492 30. S10 = 195 4. n 5. S27 = 2268 |
|
Ответы: 10. х13 = -32 20. S8 = 30. S18 = 6795 4. n 5. S33 = 1683 |
Ответы: 10. х3 = -2 20. S10 = 330 30. S6 = 4. n 5. S20 = 1260 |
|
Ответы: 10. b4 = 34 20. S12 = 90 30. S10 = 160 4. n = 10, n 5. S22 = 759 |
Ответы: 10. b16 = 20. S10 = 45 30. S8 = 4. n 5. S10 = 165 |
|
Ответы: 10. b6 = 20. S8 = 30. S12 = 4. n 5. S16 = 816 |
Ответы: 10. a82 = 326 20. S16 = 360 30. S8 = 268 4. n = 5. S51 = 5304 |
|
Ответы: 10. a232 = 1163 20. S6 = 102 30. S30 = -12810 4. n = -28, n 5. S20 = 840 |
Ответы: 10. a15 = -84 20. S6 = -9 30. S30 = 2085 4. n = 25,5, n 5. S40 = 3280 |
|
1 вариант |
2 вариант |
|
1. Зная первые два члена арифметической прогрессии 3,4; -0,2;…; Найти следующие за ними четыре ее члена |
1. Зная первые два члена арифметической прогрессии 2,8; -0,4;…; Найти следующие за ними четыре ее члена |
|
2. В арифметической прогрессии (bn) известны b1=-0,8, d=4. Найти: А) b3 Б) b7 В) b24 Г) bk+1 |
2. В арифметической прогрессии (bn) известны b1=-1,2; d=3. Найти: А) b4 Б) b8 В) b21 Г) bk+2 |
|
3. Найти разность арифметической прогрессии (an), если: А) a1=16, a8=37; Б) a1=4, а18=-11. |
3. Найти разность арифметической прогрессии (an), если: А) a1=5, a8=19; Б) a1=2, а11=-5. |
|
4. Последовательность задана формулой xn=5n-2. Найти: x6 |
4. Последовательность задана формулой xn=6n-1. Найти: x4 |
|
3 вариант |
4 вариант |
|
1. Зная первые два члена арифметической прогрессии 3,4; -0,2;…; Найти следующие за ними четыре ее члена |
1. Зная первые два члена арифметической прогрессии 2,8; -0,4;…; Найти следующие за ними четыре ее члена |
|
2. В арифметической прогрессии (bn) известны b1=-0,8, d=4. Найти: А) b3 Б) b7 В) b24 Г) bk+1 |
2. В арифметической прогрессии (bn) известны b1=-1,2; d=3. Найти: А) b4 Б) b8 В) b21 Г) bk+2 |
|
3. Найти разность арифметической прогрессии (an), если: А) a1=16, a8=37; Б) a1=4, а18=-11. |
3. Найти разность арифметической прогрессии (an), если: А) a1=5, a8=19; Б) a1=2, а11=-5. |
|
4. Последовательность задана формулой xn=5n-2. Найти: x6 |
4. Последовательность задана формулой xn=6n-1. Найти: x4 |
|
5 вариант |
6 вариант |
|
1. Зная первые два члена арифметической прогрессии 3,4; -0,2;…; Найти следующие за ними четыре ее члена |
1. Зная первые два члена арифметической прогрессии 2,8; -0,4;…; Найти следующие за ними четыре ее члена |
|
2. В арифметической прогрессии (bn) известны b1=-0,8, d=4. Найти: А) b3 Б) b7 В) b24 Г) bk+1 |
2. В арифметической прогрессии (bn) известны b1=-1,2; d=3. Найти: А) b4 Б) b8 В) b21 Г) bk+2 |
|
3. Найти разность арифметической прогрессии (an), если: А) a1=16, a8=37; Б) a1=4, а18=-11. |
3. Найти разность арифметической прогрессии (an), если: А) a1=5, a8=19; Б) a1=2, а11=-5. |
|
4. Последовательность задана формулой xn=5n-2. Найти: x6 |
4. Последовательность задана формулой xn=6n-1. Найти: x4 |
Контрольная работа по алгебре в 9 классе «Арифметическая прогрессия» с ответами и решениями (вариант 1). Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Алгебра 9 Макарычев К-6 В-1.
Другие варианты: К-6 Вариант 2 К-6 Вариант 3 К-6 Вариант 4
Вернуться к Списку контрольных работ (ОГЛАВЛЕНИЕ)
§ 9. Арифметическая прогрессия.
КР-6. Вариант 1 (транскрипт заданий)
- Найдите тридцатый член арифметической прогрессии (аn), если а1 = –25 и d = 4.
- Найдите сумму первых пятнадцати членов арифметической прогрессии (аn), если а1 = 2 и а2 = 5.
- Является ли число –6 членом арифметической прогрессии (сn), в которой с1 = 30 и с7 = 21?
- Найдите сумму первых двадцати членов последовательности, заданной формулой bn = 2n + 1.
- Найдите сумму всех натуральных чисел, кратных 4 и не превышающих 150.
Алгебра 9 Макарычев К-6 В-1
ОТВЕТЫ на контрольную работу:
№ 1. Найдите тридцатый член арифметической прогрессии (аn), если а1 = –25 и d = 4.
Дано: (an) – арифметическая прогрессия; a1 = –25; d = 4.
Найти: a30 – ?
Решение: Формула n-го члена арифметической прогрессии: an = a1 + d (n – 1), где a1 – первый член прогрессии, d – разность прогрессии, n – количество её членов. С помощью этой формулы запишем искомый тридцатый член заданной прогрессии:
a30 = a1 + d (30 – 1) = a1 + 29d. Подставим в полученное выражение известные нам по условию значения:
a30 = a1 + 29d = –25 + 29 • 4 = –25 + 116 = 91.
ОТВЕТ: a30 = 91.
№ 2. Найдите сумму первых пятнадцати членов арифметической прогрессии (аn), если а1 = 2 и а2 = 5.
ОТВЕТ: 345.
Решение:
№ 3. Является ли число –6 членом арифметической прогрессии (сn), в которой с1 = 30 и с7 = 21?
ОТВЕТ: Да.
Решение:
№ 4. Найдите сумму первых двадцати членов последовательности, заданной формулой bn = 2n + 1.
ОТВЕТ: 440
Решение:
№ 5. Найдите сумму всех натуральных чисел, кратных 4 и не превышающих 150.
ОТВЕТ: 2812.
Решение:
Вы смотрели: Контрольную работу по алгебре 9 класс «Арифметическая прогрессия» с ответами и решениями. Представленная контрольная работа ориентирована на УМК Макарычева. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки указанного учебного пособия. Алгебра 9 Макарычев К-6 В-1.
Другие варианты: К-6 Вариант 2 К-6 Вариант 3 К-6 Вариант 4
Вернуться к Списку контрольных работ (ОГЛАВЛЕНИЕ)
(c) В учебных целях использованы цитаты из пособия: «Алгебра. Дидактические материалы 9 класс / Макарычев, Миндюк, Крайнева — М.: Просвещение».
Контрольная работа № 4 «Арифметическая прогрессия»
Вариант 1
№1. Найдите седьмой член арифметической прогрессии, у которой первый член равен 12, а разность равна -5.
№2. Последовательность (ап) – арифметическая прогрессия, а35=-304, d=-6. Найдите а1.
№3. Найдите сумму первых сорока членов арифметической прогрессии, у которой х1=38, х40=72.
№4. Найдите сумму первых восьми членов арифметической прогрессии (сп): 5,5; 6,3; …
№5. Найдите первый член и разность арифметической прогрессии, если с9=53, с19=46.
№6. Найдите сумму первых девяти членов арифметической прогрессии, если уп=-5п+3.
№7. Укажите первый положительный член арифметической прогрессии, если а8=-61, d=2,5.
№8. Найдите сумму всех нечетных чисел от 33 до 61 включительно.
Контрольная работа № 4 «Арифметическая прогрессия»
Вариант 2
№1. Найдите восьмой член арифметической прогрессии, у которой первый член равен -45, а разность равна 4.
№2. Последовательность (ап) – арифметическая прогрессия, а20=153, d=6. Найдите а1.
№3. Найдите сумму первых шестидесяти членов арифметической прогрессии, у которой с1=-8, с60=44.
№4. Найдите сумму первых семи членов арифметической прогрессии (сп): -35; -28; …
№5. Найдите первый член и разность арифметической прогрессии, если х8=31, х18=16.
№6. Найдите сумму первых шести членов арифметической прогрессии, если сп=-3п+4.
№7. Укажите первый отрицательный член арифметической прогрессии, если а7=45, d=-1,5.
№8. Найдите сумму всех четных чисел от 22 до 54 включительно.
Контрольная работа № 4 «Арифметическая прогрессия»
Вариант 3
№1. Найдите шестой член арифметической прогрессии, у которой первый член равен 18, а разность равна -4.
№2. Последовательность (ап) – арифметическая прогрессия, а45=-260, d=-4. Найдите а1.
№3. Найдите сумму первых пятидесяти членов арифметической прогрессии, у которой с1=24, с50=98.
№4. Найдите сумму первых семи членов арифметической прогрессии (сп): -18; -15; …
№5. Найдите первый член и разность арифметической прогрессии, если с6=48, с16=24.
№6. Найдите сумму первых восьми членов арифметической прогрессии, если хп=-7п+5.
№7. Укажите первый положительный член арифметической прогрессии, если а12=-83, d=4,5.
№8. Найдите сумму всех нечетных чисел от 27 до 65 включительно.
Контрольная работа № 4 «Арифметическая прогрессия»
Вариант 4
№1. Найдите девятый член арифметической прогрессии, у которой первый член равен -65, а разность равна 6.
№2. Последовательность (ап) – арифметическая прогрессия, а20=153, d=6. Найдите а1.
№3. Найдите сумму первых тридцати членов арифметической прогрессии, у которой с1=-14, с30=29,5.
№4. Найдите сумму первых шести членов арифметической прогрессии (сп): -33; -29; …
№5. Найдите первый член и разность арифметической прогрессии, если у12=47, у22=77.
№6. Найдите сумму первых восьми членов арифметической прогрессии, если сп=-6п+5.
№7. Укажите первый отрицательный член арифметической прогрессии, если а7=35, d=-2,5.
№8. Найдите сумму всех четных чисел от 18 до 56 включительно.
Ответы:
|
№ задания |
1 |
2 |
3 |
4 |
Критерии оценивания |
|
1 |
-18 |
-17 |
-2 |
-17 |
1 балл |
|
2 |
-100 |
39 |
-84 |
39 |
1 балл |
|
3 |
2200 |
1080 |
3050 |
232,5 |
1 балл |
|
4 |
66,4 |
-98 |
-63 |
-138 |
1 балл |
|
5 |
58,6 -0,7 |
41,5 -1,5 |
60 -2,4 |
14 3 |
2 балла |
|
6 |
-198 |
-39 |
-212 |
-176 |
2 балла |
|
7 |
п=33 1,5 |
п =38 -1,5 |
п =31 2,5 |
п =22 -2,5 |
3 балла |
|
8 |
705 |
646 |
920 |
740 |
3 балла (1 балл в случае, если сумма подсчитана без использования формул) |
|
Итого: тах=14 баллов |
Оценка «5»: 11-14 баллов
Оценка «4»: 7-10 баллов
Оценка «3»: 3-6 баллов
Оценка «2»: 0-2 балла
-
Данный тест по теме «АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ, ЕЕ СВОЙСТВА. ФОРМУЛА n-го ЧЛЕНА АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ» предназначен для обучающихся 9-х классов , для проверки усвоения нового материала.
-
Тест создан для определения уровня усвоения знаний по теме «Арифметическая прогрессия».
-
Контрольная работа по темам «Геометрическая и арифметическая прогрессии»
-
Тест по теме «Арифметическая прогрессия» предназначен для обучающихся 9-ых классов, рекомендован для подготовки к ОГЭ
-
Тест предназначен для проверки базовых знаний по теме. Может быть использован для самопроверки при подготовке к итоговой аттестации.
-
Данный тест создан для проверки знаний по теме «Арифметическая прогрессия»
-
Привет, ребята! Пришло время показать свои знания на практике.
-
Данная самостоятельная работа может быть использована для провверки знаний учащихмя по теме «Прогрессии»
-
Вводный тест направлен на повторение и использование формул по теме: «Арифметичская прогрессия».
-
Тест по теме: «Арифметическая прогрессия» направлен на контроль знаний и умений учащихся, применение формул.
Тест состоит из трех вопросов. -
Тест для учащихся 9 класса. Вопросы теста предполагают как выбор из вариантов, так и ввод ответов.
-
Тест для учащихся 9 класса. Вопросы теста предполагают как выбор из вариантов, так и ввод ответов.







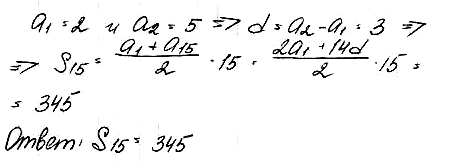
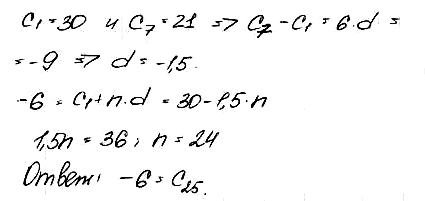
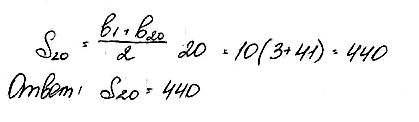
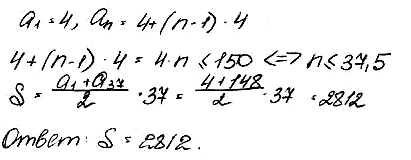
 № варианта
№ варианта















