Проверочная работа по теме подобие треугольников рекомендуемое время выполнения 15 минут - Контакты компаний и предприятий на Atlaso.ru

Проверочная работа по теме
«Признаки подобия треугольников»

Вариант 3.

1.
Сформулируйте утверждения о
пропорциональных отрезках в прямоугольном треугольнике. Сделайте рисунок:
прямоугольный треугольник с прямым углом В и высотой ВН. Запишите утверждения,
используя данный рисунок.

2.
Высота, проведенная из вершины прямого
угла прямоугольного треугольника, равна 6 см и делит гипотенузу на отрезки,
один из которых больше другого на 5 см. Найдите стороны треугольника.

3.
Дано: АО
= 5,1 см, ОВ = 6,3 см,

СО
= 8,4 см, ОD = 6,8 см.

Доказать:
АВ || СD.

Найти:
а) б)

Проверочная
работа по теме «Признаки подобия треугольников»

Вариант 3.

3. Дано:
АО = 5,1 см, ОВ = 6,3 см,

СО
= 8,4 см, ОD = 6,8 см.

Доказать:
АВ || СD.

Найти:
а) б)

Проверочная
работа по теме «Признаки подобия треугольников»

Вариант 3.

3.
Дано: АО
= 5,1 см, ОВ = 6,3 см,

СО
= 8,4 см, ОD = 6,8 см.

Доказать:
АВ || СD.

Найти:
а) б)

Проверочная
работа по теме «Признаки подобия треугольников»

Вариант 3.

3.
Дано: АО
= 5,1 см, ОВ = 6,3 см,

СО
= 8,4 см, ОD = 6,8 см.

Доказать:
АВ || СD.

Найти:
а) б)

Источник

Определение подобных треугольников.

Avatar

08.02.2022.
Тест. Геометрия, 8 класс

Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного
использования.
Администрация сайта не
проверяет возможные ошибки,
которые могут встретиться в тестах.

Тест содержит 10 вопросов по теме «Определение подобных треугольников», время на выполнение теста 15 минут.

Список вопросов теста

Вопрос 1

Какое из следующих утверждений верно?

Варианты ответов

Два треугольника называются подобными, если углы и стороны одного треугольника пропорциональны углам и сторонам другого треугольника.
Два треугольника называются подобными, если стороны одного треугольника пропорциональны сторонам другого треугольника.
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сторонам другого треугольника.
Два треугольника называются подобными, если стороны одного треугольника равны сторонам другого треугольника.

Вопрос 2

Какое из следующих утверждений верно?

Варианты ответов

Отношение площадей двух подобных треугольников равно коэффициенту подобия.
Отношение площадей двух подобных треугольников равно половине коэффициента подобия.
Отношение площадей двух подобных треугольников равно половине квадрата коэффициента подобия.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Вопрос 3

Верно ли утверждение: отношение периметров двух подобных треугольников равно коэффициенту подобия.

Варианты ответов

верно
не верно

Вопрос 4

Могут ли быть подобными прямоугольный и равнобедренный треугольники?

Варианты ответов

могут
не могут

Вопрос 5

Треугольники ABC и MNK подобны, причем ∠A=∠N, ∠B=∠K. Назовите сторону, сходственную со стороной MN.

Варианты ответов

АВ
ВС
АС

Вопрос 6

Треугольники KPF и ЕМТ подобны, причем КР : МЕ = PF : МТ = KF : ET, угол F = 30°, угол Е = 49°. Чему равен угол М?

Варианты ответов

Вопрос 7

Найти стороны треугольника А1В1С1, подобного треугольнику АВС, если

АВ = 6, ВС= 12, АС = 9 и k = 3 .

Варианты ответов

18, 36, 27
9, 15, 12
2, 4, 3

Вопрос 8

Две сходственные стороны подобных треугольников равны 8 см и 4 см. Периметр второго треугольника равен 12 см. Чему равен периметр первого треугольника ?

Вопрос 9

Две сходственные стороны подобных треугольников равны 9 см и 3 см. Площадь второго треугольника равна 9 см2. Чему равна площадь первого треугольника ?

Вопрос 10

Подобны ли треугольники АВС и DEF, сли угол А равен 106 градусов, угол В равен 34 градуса, угол Е равен 106 градусов, угол F равен 40 градусов, АС = 4, 4 см, АВ = 5,2 см, ВС = 7,6 см, DE = 15,6 см, DF = 22,8 см, EF = 13.2 см?

Варианты ответов

Подобны
Не подобны
Не хватает данных

Источник

Проверочная работа предназначена для проверки обучающихся по теме «Подобие треугольников». Задания составлены так, чтобы ученики показали не только знания теоретического материала, но и умение применять определения, признаки и свойства подобных треугольников при решении задач. Формулировки ответов тестовой части очень похожи, надо знать точные определения, чтобы справиться с работой.

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Источник

1 вариант

2 вариант

Записать определение подобия треугольников ADF и CKO (рисунок, обозначение, пропорциональность соответствующих сторон)

Записать определение подобия треугольников DAB и NMK (рисунок, обозначение, пропорциональность соответствующих сторон)

Треугольник АВС и MNP подобны.

Известно, что АВ = 3см, АС = 7см,

МР = 21см.

Найдите сторону MN

Треугольник КВТ и MNP подобны.

Известно, что КВ = 8 см, КТ = 13см,

МР = 26см.

Найдите сторону MN.

Записать определение 1 признака подобия треугольников

3 вариант

4 вариант

Записать определение подобия треугольников DFC и AOK (рисунок, обозначение, пропорциональность соответствующих сторон)

Записать определение подобия треугольников COB и DAE (рисунок, обозначение, пропорциональность соответствующих сторон)

Треугольники АВС и DEF подобны. Угол А равен

углу D, угол С равен углу F, EF= 14, DF=20, ВС=21.

Найдите АС.

Треугольники АВС и DEF подобны. Угол А равен

углу D, угол С равен углу F, EF= 14, DF=20, ВС=21.

Найдите АС.

Треугольники АВС и DEF подобны. Угол А равен

углу D, угол С равен углу F, EF= 14, DF=20, ВС=21.

Найдите АС.

Треугольники АВС и DEF подобны. Угол А равен

углу D, угол С равен углу F, EF= 14, DF=20, ВС=21.

Найдите АС.

Треугольники АВС и DEF подобны. Угол А равен

углу D, угол С равен углу F, EF= 14, DF=20, ВС=21.

Найдите АС.

Треугольники АВС и DEF подобны. Угол А равен углу D, угол С равен углу F, EF= 14, DF=20, ВС=21. Найдите АС.

Треугольники KPF и ЕМТ подобны, причём , угол Fравен 20⁰, угол Е равен 40⁰. Найдите остальные углы этих треугольников.

Записать определение 1 признака подобия треугольников

1 вариант

вариант

Треугольник АВС и MNP подобны.

Известно, что АВ = 3см, АС = 7см,

МР = 21см.

Найдите сторону MN

Треугольник КВТ и MNP подобны.

Известно, что КВ = 8 см, КТ = 13см,

МР = 26см.

Найдите сторону MN.

Записать определение 1 признака подобия треугольников

3 вариант

4 вариант

Треугольники АВС и DEF подобны. Угол А равен

углу D, угол С равен углу F, EF= 14, DF=20, ВС=21.

Найдите АС.

Треугольники АВС и DEF подобны. Угол А равен

углу D, угол С равен углу F, EF= 14, DF=20, ВС=21.

Найдите АС.

Треугольники АВС и DEF подобны. Угол А равен

углу D, угол С равен углу F, EF= 14, DF=20, ВС=21.

Найдите АС.

Треугольники АВС и DEF подобны. Угол А равен

углу D, угол С равен углу F, EF= 14, DF=20, ВС=21.

Найдите АС.

Треугольники АВС и DEF подобны. Угол А равен

углу D, угол С равен углу F, EF= 14, DF=20, ВС=21.

Найдите АС.

Треугольники АВС и DEF подобны. Угол А равен углу D, угол С равен углу F, EF= 14, DF=20, ВС=21. Найдите АС.

Записать определение 1 признака подобия треугольников

Источник

Тест по теме: «Подобие треугольников» (8 класс)

1 вариант

1. Укажите условия, при которых

были бы подобны по

третьему признаку.

а)

2. У треугольников АВС и DEF равны углы А и D. Какого условия не достает

для того, чтобы утверждать, что эти треугольники подобны по первому признаку:

а)

3. В треугольниках АВС и MNK

00000

60,70,60,70,50  KMCBА

Чему равен угол N?

а)50

; б)60

; в)70

4. Установите по рисунку, верно ли данное утверждение:

а)ДА; б)НЕТ; в)Не возможно установить.

, АВ=4, ВС=6, АС=7, А

=8. Сторона В

равна:

а)3; б)12; в)14.

6. В треугольниках ABC и

Если ВС=10, то В

равна:

а)25; б) 4; в) 5.

7. Соответствующие катеты двух подобных прямоугольных треугольников

равны 5 дм и 10 дм. Найдите гипотенузу большего треугольника, если гипотенуза

меньшего равна 7 дм.

а)14; б)

Тест по теме: «Подобие треугольников» (8 класс)

2 вариант

1. Укажите условия, при которых

были бы подобны по первому

признаку.

а)

2. У треугольников АВС и DEF равны углы А и D. Какого условия не достает

для того, чтобы утверждать, что эти треугольники подобны по второму признаку:

а)

3. В треугольниках АВС и MNK

00000

35,70,80,65,35  KMCBА

Чему равен угол N?

а)35

; б)75

; в)80

4. Установите по рисунку, верно ли данное утверждение:

а)ДА; б)НЕТ; в)Не возможно установить.

, АВ=2, ВС=3, АС=1, А

=8. Сторона В

равна:

а)12; б)4; в)6.

6. В треугольниках ABC и

Если ВС=12, то В

равна:

а)6; б) 18; в) 3.

7. Соответствующие катеты двух подобных прямоугольных треугольников

равны 6 м и 18 м. Найдите гипотенузу меньшего треугольника, если гипотенуза

большего равна 27 дм.

а)

Теоретический опрос «Подобие треугольников» (8 класс)

Подобные треугольники — треугольники, у которых соответственно равны, а одного

пропорциональны сторонам другого треугольника.

Коэффициент — число k, равное отношению сторон подобных

треугольников.

Сходственные стороны подобных треугольников — стороны, лежащие напротив

углов.

1) Первый признак

Если два одного треугольника соответственно равны .

другого треугольника, то треугольники .

2) Третий признак

Если одного треугольника трём сходственным сторонам

другого, то подобны.

3) Свойства подобных треугольников:

 Отношение подобных треугольников равно квадрату подобия

 Отношение равно коэффициенту подобия.

Теоретический опрос «Подобие треугольников» (8 класс)

Подобные треугольники — треугольники, у которых соответственно равны, а одного

пропорциональны сторонам другого треугольника.

Коэффициент — число k, равное отношению сторон подобных

треугольников.

Сходственные стороны подобных треугольников — стороны, лежащие напротив

углов.

4) Первый признак

Если два одного треугольника соответственно равны .

другого треугольника, то треугольники .

5) Третий признак

Если одного треугольника трём сходственным сторонам

другого, то подобны.

6) Свойства подобных треугольников:

 Отношение подобных треугольников равно квадрату подобия

 Отношение равно коэффициенту подобия.

Тест. Подобные треугольники

Заполните пропуски (многоточия), чтобы

получилось верное высказывание.

ВАРИАНТ 1

1. Запись

означает, что отрезки

АВ

и CD … отрезкам MN и FT.

2. На рисунке изображен параллелограмм

ABCD, поэтому подобными являются

треугольники … и ….

3. На рисунке АС || МК, поэтому

треугольник МВК подобен треугольнику ….

4. Если угол В равен …, то изображенные на

рисунке треугольники ABC и KNM подобны.

5. На рисунке МК || АС, АВ = 15 см, МВ = 5

см, АС = 30 см. Длина отрезка МК = … .

6. На рисунке изображена трапеция ABCD,

причем АО = 27 см, ВО = 18 см, ОС = 21 см.

Длина отрезка OD равна ….

7. Площади двух подобных многоугольников

равны 75 см

и 300 см

. Одна из сторон второго

многоугольника равна 9 см. Поэтому

сходственная сторона первого многоугольника

равна ….

8. Сходственные стороны двух подобных

треугольников равны 5 дм и 10 дм. Периметр

первого треугольника равен 60 дм, периметр

второго треугольника равен ….

9*. Известно, что ∆АВС — прямоугольный

треугольник с прямым углом С, a CD — высота,

проведенная из вершины С к гипотенузе АВ.

Из подобия треугольников … и … следует, что

=AB*AD.

Тест. Подобные треугольники

Заполните пропуски (многоточия), чтобы

получилось верное высказывание.

ВАРИАНТ 2

1. Запись

означает, что отрезки CD

и MP … отрезкам AN и BK.

2. На рисунке изображен параллелограмм

АВСD, поэтому подобными являются

треугольники … и ….

3. На рисунке АВ || KD, поэтому треугольник

DKC подобен треугольнику ….

4. Если АС = …, KN = …, то изображенные на

рисунке треугольники ABC и KNM подобны.

5. На рисунке МК || АС, ВК = 20 см, МК = 10

см, ВС = 30 см. Длина отрезка АС = … .

6. На рисунке изображена трапеция ABCD,

причем АО = 20 см, ОС = 3 см, AD = 30 см. Длина

отрезка ВС = … .

7. Сходственные стороны двух подобных

многоугольников равны 20 см и 10 см. Площадь

большего многоугольника равна 160 см

площадь меньшего многоугольника равна ….

8. Периметры подобных треугольников равны

75 см и 300 см. Одна из сторон большего

треугольника равна 20 см, сходственная сторона

меньшего треугольника равна ….

9*. Известно, что ∆АВС — прямоугольный

треугольник с прямым углом С, a CD — высота,

проведенная из вершины С к гипотенузе АВ. Из

подобия треугольников … и … следует, что

ВС

= AB*BD.

Тест. Подобные треугольники

Установите, истинны или ложны

следующие высказывания:

Вариант 1

1. Два одноименных многоугольника

называются подобными, если углы одного

соответственно равны углам другого и

сходственные стороны пропорциональны.

2. Если два угла одного треугольника

соответственно равны двум углам другого

треугольника, то такие треугольники

подобны.

3. Два равносторонних треугольника

всегда подобны.

4. Если три стороны одного

треугольника соответственно

пропорциональны трем сторонам другого

треугольника, то такие треугольники

подобны.

5. Периметры подобных

многоугольников относятся как

сходственные стороны.

6. Стороны одного треугольника имеют

длины 3 см, 4 см и 6 см. Стороны другого

треугольника равны 9 см, 14 см и 18 см.

Подобны ли эти треугольники?

7. Два равнобедренных треугольника

подобны, если их углы при вершине

равны, и боковые стороны

пропорциональны.

8. Два прямоугольных треугольника

подобны, если имеют по равному острому

углу.

9. Если два угла одного треугольника

равны 60° и 50°, а два угла другого

треугольника равны 50° и 80°, то такие

треугольники подобны.

10. Если каждую сторону треугольника

уменьшить в 2,5 раза, то получится

треугольник, подобный первоначальному.

11.Два ромба всегда подобны.

12. Два равнобедренных треугольника

подобны, если их основания

пропорциональны.

Тест. Подобные треугольники

Установите, истинны или ложны

следующие высказывания:

Вариант 2.

1. Два треугольника называются

подобными, если их углы соответственно

равны и стороны пропорциональны.

2. Если два треугольника имеют по

равному углу, а стороны, заключающие

эти углы, пропорциональны, то такие

треугольники подобны.

3. Два квадрата всегда подобны.

4. Если три стороны одного

треугольника соответственно равны трем

сторонам другого треугольника, то такие

треугольники подобны.

5. Стороны одного треугольника имеют

длины 4 м, 5 м и 6 м. Стороны другого

треугольника равны 12 м, 8 м и 10 м.

Тогда эти треугольники подобны.

6. Площади подобных треугольников

относятся как квадраты сходственных

сторон.

7. Два параллелограмма всегда подобны.

8. Если два угла одного треугольника

равны 45° и 75°, а два угла другого

треугольника равны 60° и 45°, то такие

треугольники подобны.

9. Два прямоугольных треугольника

подобны, если катеты одного

треугольника соответственно

пропорциональны катетам другого.

10. Если каждую сторону треугольника

уменьшить в 3 раза, то получится

треугольник, подобный первоначальному.

11. Два равнобедренных треугольника

подобны, если угол при основании одного

треугольника равен углу при основании

другого.

12. Два равнобедренных треугольника

подобны, если их боковые стороны

пропорциональны.

Признаки подобия треугольников

Вариант №1

1. У треугольников АВС и KLM равны углы А и К. Какого условия недостаёт,

чтобы утверждать, Что эти треугольники подобны по первому признаку?

; 2) АВ = KL, АС = КМ; 3)

; 4) угол В равен углу L.

2. Стороны одного треугольника равны 3 см, 6 см и 7 см, а стороны подобного ему

треугольника равны 15 см и 35 см. Найдите длину третьей стороны:

1) 70 см; 2) 7,5 см; 3) 30 см; 4) ответ не указан.

3. Стороны угла К пересечены прямыми АВ и СД, причём точки А и С лежат на

одной стороне угла (А лежит между К и С), а В и Д – на другой стороне (В лежит

между К и Д). Какой должна быть длина отрезка АС, чтобы прямые АВ и СД были

параллельны, если КА = 3,6 см, КВ = 4,8 см, ВД = 2,4 см?

1) 5,4 см; 2) 1,8 см; 3) 3,2 см; 4) 2 см.

4. ВС и АД – основания трапеции АВСД. Угол АВД равен углу ВСД. ВС = 4 см,

ДС = 6 см, ВД = 8 см. Найдите АД:

1) 16 см; 2) 3 см; 3) 12 см; 4) 10 см.

5. На сторонах АВ и ВС треугольника АВС отмечены соответственно точки К и L,

так , что KL параллельно АС. Площадь треугольника КBL равна 84 см², а площадь

треугольника АВС равна 336 см², АС = 30 см. Найдите КL:

1) 7,5 см; 2) 10 см; 3) 15 см; 4) ответ не указан.

Признаки подобия треугольников

Вариант №2

1.Какие условия должны быть выполнены для того, чтобы треугольники АВС и

КLМ были подобны по второму признаку?

2. Стороны одного треугольника равны 3 см, 7 см и 6 см, а две стороны подобного

ему треугольника равны 10,5 см и 4,5 см. Найдите длину третьей стороны:

1) 4 см; 2) 9 см; 3) 4,5 см; 4) ответ не указан.

3. Дан треугольник АВС и внутри него отрезок КМ, параллельный АС, причём

Найдите МС, если АВ = 18 см, ВК = 6 см, ВМ = 4 см:

1) 12 см; 2) 16 см; 3) 6 см; 4) 8 см.

4. В трапеции АВСД углы АВС и АСД равны. Найдите диагональ АС, если

основания ВС и АД соответственно равны 24 см и 54 см:

1) 18 см; 2) 30 см; 3) 36 см; 4) 72 см.

5. Дан треугольник АВС,

причём отрезок КМ параллельный АС.

Площадь треугольника КВМ равна 9 см², ВМ = 6 см, МС = 2 см. Найдите площадь

треугольника АВС:

1) 12 см²; 2) 16 см²; 3) 81 см²; 4) ответ не указан

«Подобие треугольников» (8 класс)

Найти подобные треугольники на чертежах:

Задание 1:

Задание 2:

Источник

Контрольная работа № 3 по геометрии в 8 классе «Признаки подобия треугольников» с ответами и решениями (3 уровня сложности по 2 варианта). УМК Атанасян и др. (Просвещение). Поурочное планирование по геометрии для 8 класса. Урок 38. Геометрия 8 класс. Контрольная работа № 3 по теме «Признаки подобия треугольников».

Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.

ХОД УРОКА

1. Организационный момент

Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.

2. Выполнение контрольной работы

Контрольная работа по геометрии.
I уровень сложности

Вариант 1

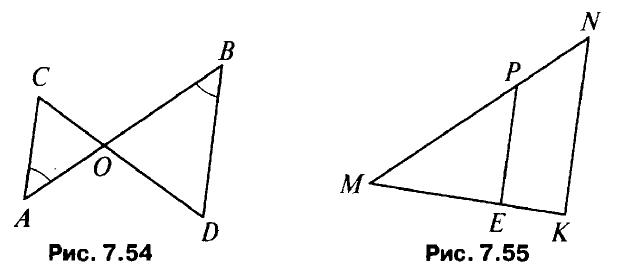
Дано: ∠A = ∠B, СО = 4, DO = 6, АО = 5 (рис. 7.54). Найти: а) ОВ, б) АС, BD: в) S_AOC, S_BOD.
В треугольнике АВС АВ = 4 см, ВС = 1 см, АС = 6 см, а в треугольнике MNK МК = 8 см, MN = 12 см, KN = 14 см. Найдите углы треугольника MNK, если ∠A = 80°, ∠B = 60°.
Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК||АС, ВМ : AM = 1 : 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см.
* В трапеции ABCD (AD и ВС основание) диагонали пересекаются в точке О, AD = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника AOD равна 45 см².

Вариант 2

Дано: РЕ||NK, МР = 8, MN = 12, ME = 6 (рис. 7.55). Найти: а) МК; б) РЕ : NK; в) S_MPE : S_MNK.
В ΔАВС АВ = 12 см, ВС = 18 см, ∠В = 70°, а в ΔMNK MN = 6 см, NK = 9 см, ∠N = 70°. Найдите сторону АС и угол С треугольника АВС, если МК = 1 см, ∠K = 60°.
Отрезки АВ и CD пересекаются в точке О так, что ∠ACO = ∠BDO, АО : ОВ = 2:3. Найдите периметр треугольника АСО, если периметр треугольника BOD равен 21 см.
* В трапеции ABCD (AD и ВС основания) диагонали пересекаются в точке О, S_AOD= 32 см², S_BOC = 8 см². Найдите меньшее основание трапеции, если большее из них равно 10 см.

Контрольная работа по геометрии.
II уровень сложности

Вариант 1

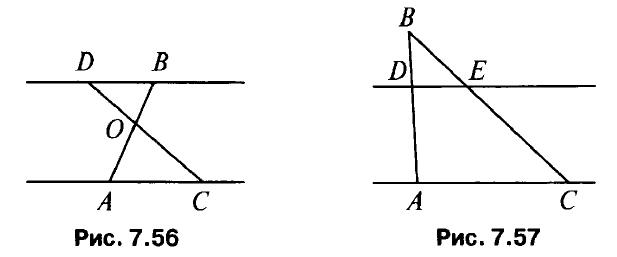
Дано: АО = 6,8 см, СО = 8,4 см, ОВ = 5,1 см, OD = 6,3 см (рис. 7.56).
Доказать: АС||BD. Найти: a) DB : АС, б) P_AOC : P_DBO, в) S_DBO : S_AOC.
Диагонали ромба ABCD пересекаются в точке О, BD = 16 см. На стороне АВ взята точка К так, что ОК ⊥ АВ и ОК = 4√3 см. Найдите сторону ромба и вторую диагональ.
В выпуклом четырехугольнике ABCD АВ = 9 см, ВС = 8 см, CD = 16 см, AD = 6 см, BD = 12 см. Докажите, что ABCD — трапеция.
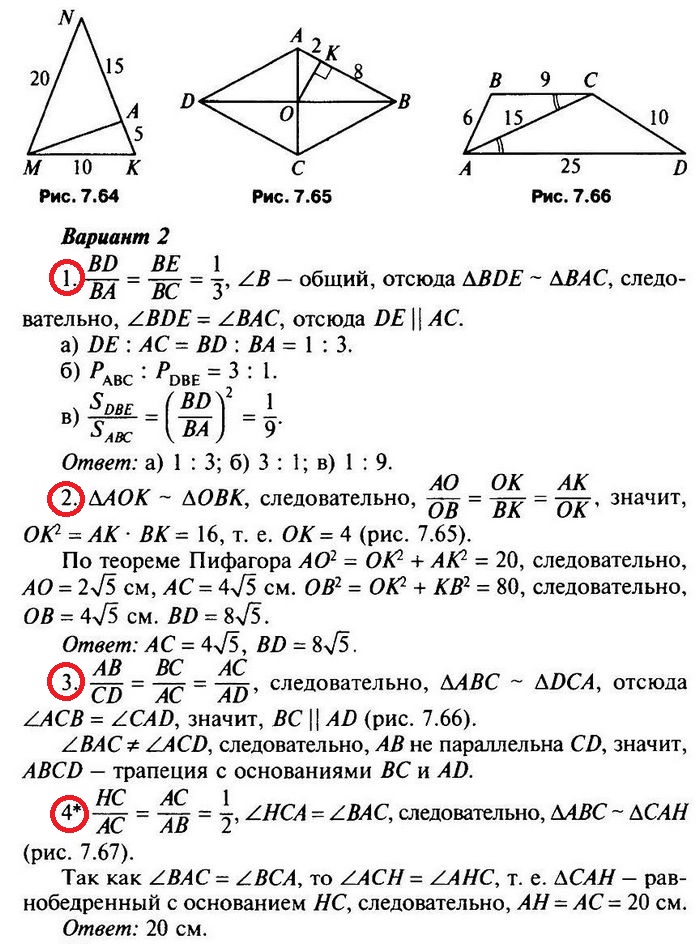
* В равнобедренном треугольнике MNK с основанием МК, равным 10 см, MN = NK = 20 см. На стороне NK лежит точка А так, что AК : AN =1 : 3. Найдите AM.

Вариант 2

Дано: BD = 3,1 см, BE = 4,2 см, ВА = 9,3 см, ВС = 12,6 см (рис. 7.57).
Доказать: DE||АС. Найти, a) DE : АС, б) P_АВС : P_DBE, в) S_DBE : S_ABC.
Диагонали ромба ABCD пересекаются в точке О. На стороне АВ взята точка К так, что ОК ⊥ АВ, АК = 2 см, ВК = 8 см. Найдите диагонали ромба.
ABCD — выпуклый четырехугольник, АВ = 6 см, ВС = 9 см, CD = 10 см, DA = 25 см, АС = 15 см. Докажите, что ABCD — трапеция.
* В равнобедренном треугольнике АВС АВ = ВС = 40 см, АС = 20 см. На стороне ВС отмечена точка Н так, что ВН : НС = 3 : 1. Найдите АН.

Контрольная работа по геометрии.
III уровень сложности

Вариант 1

К диагонали АС прямоугольника ABCD проведен перпендикуляр DE так, что АЕ = 8 см, СЕ = 4 см.
Найти: а) АВ : ВС, б) P_ABCD; в) S_ABCD.
ABCD — прямоугольная трапеция (∠A = 90°). Точка Е лежит на основании AD так, что СЕ перпендикулярен AD и АЕ = DE. Точка О — середина диагонали АС. Докажите, что ВО : ВС = = CD : AD. Найдите площадь пятиугольника ABOCD, если площадь треугольника ACD равна 20 см².
Диагональ BD трапеции ABCD делит ее на два подобных треугольника. Найдите BD, если основания ВС и AD равны 8 см и 12,5 см соответственно.
* На сторонах MN и NK треугольника MNK взяты точки А и В соответственно так, что ∠ABN = ∠M. Отрезок NE является биссектрисой угла ANB, АЕ : ЕВ = 2 : 3. Найдите отношение NК к MN.

Вариант 2

К диагонали BD прямоугольника ABCD проведен перпендикуляр АК так, что ВК = 5 см, DK = 15 см.
Найти: а) ВС : CD; б) P_BCD; в) S_BCD.
В прямоугольной трапеции ABCD ∠D = 90°. Точка К лежит на основании AD так, что АК = KD и ВК перпендикулярно ВС. Точка О — середина диагонали BD. Докажите, что АВ : AD = ВО : ВС. Найдите площадь треугольника ABD, если площадь пятиугольника ABOCD равна 30 см².
Диагональ АС трапеции ABCD равна 8 см и делит ее на два подобных треугольника. Найдите основание ВС, если AD равно 16 см.
* На сторонах РО и PS треугольника OPS взяты точки А и В соответственно так, что ∠PAB = ∠S. Биссектриса PC треугольника OPS делит сторону OS на два отрезка так, что ОС : CS = 4 : 3. Найдите отношение РВ к РА.

3. Рефлексия учебной деятельности

В конце урока учитель раздает на каждую парту краткую запись решения задач контрольной работы.
Домашнее задание: решить задачи, с которыми ученик не справился.

Решения и ответы на контрольную работу
I уровня сложности

Нажмите, чтобы открыть и посмотреть ОТВЕТЫ

Решения и ответы на контрольную работу
II уровня сложности

Нажмите, чтобы открыть и посмотреть ОТВЕТЫ

Решения и ответы на контрольную работу
III уровня сложности

Нажмите, чтобы открыть и посмотреть ОТВЕТЫ

Критерии оценивания результатов контрольной работы

оценка «5» — правильно решены три задачи;
оценка «4» — правильно решены две задачи или правильно решена одна задача, а при решении двух других задач допущены ошибки;
оценка «3» — правильно решена одна задача;
оценка «2» — все задачи решены неправильно.

За правильно решенную дополнительную задачу (№ 5) ставится дополнительная оценка.

Вы смотрели: Геометрия 8 класс. Контрольная работа № 3. Поурочное планирование по геометрии для 8 класса. УМК Атанасян (Просвещение). Урок 38. Контрольная работа № 3 по теме «Признаки подобия треугольников» + ОТВЕТЫ и РЕШЕНИЯ.

Вернуться к Списку уроков Тематического планирования в 8 классе.

Источник

Контрольная работа № 3 по геометрии в 8 классе «Признаки подобия треугольников» с ответами УМК Атанасян (легкий уровень). Урок 38 поурочного планирования по геометрии. Геометрия 8 класс Контрольная работа 3 Уровень 1 (легкий). Цитаты использованы в учебных целях. Другие варианты:

К-3 Уровень 2 + Решения
К-3 Уровень 3 + Решения

Уровень 1 (легкий). Геометрия 8 класс

К-3 Уровень 1 Вариант 1

Дано: ∠A = ∠B, СО = 4, DO = 6, АО = 5 (рис. 7.54). Найти: а) ОВ, б) АС : BD: в) S_AOC : S_BOD.
В треугольнике АВС АВ = 4 см, ВС = 7 см, АС = 6 см, а в треугольнике MNK МК = 8 см, MN = 12 см, KN = 14 см. Найдите углы треугольника MNK, если ∠A = 80°, ∠B = 60°.
Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК||АС, ВМ : AM = 1 : 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см.
* В трапеции ABCD (AD и ВС основание) диагонали пересекаются в точке О, AD = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника AOD равна 45 см².

К-3 Уровень 1 Вариант 2

Дано: РЕ||NK, МР = 8, MN = 12, ME = 6 (рис. 7.55). Найти: а) МК; б) РЕ : NK; в) S_MPE : S_MNK.
В ΔАВС АВ = 12 см, ВС = 18 см, ∠В = 70°, а в ΔMNK MN = 6 см, NK = 9 см, ∠N = 70°. Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, ∠K = 60°.
Отрезки АВ и CD пересекаются в точке О так, что ∠ACO = ∠BDO, АО : ОВ = 2:3. Найдите периметр треугольника АСО, если периметр треугольника BOD равен 21 см.
* В трапеции ABCD (AD и ВС основания) диагонали пересекаются в точке О, S_AOD= 32 см², S_BOC = 8 см². Найдите меньшее основание трапеции, если большее из них равно 10 см.

Геометрия 8 класс Контрольная работа 3
Решения и ответы (легкий уровень):

Задания и Ответы на Вариант 1

№ 1. Дано: ∠A = ∠B, СО = 4, DO = 6, АО = 5 (рис. 7.54). Найти: а) ОВ, б) АС : BD: в) S_AOC : S_BOD.
Правильный ответ: а) 7,5; б) 2 : 3; в) 4 : 9.

№ 2. В треугольнике АВС АВ = 4 см, ВС = 7 см, АС = 6 см, а в треугольнике MNK МК = 8 см, MN = 12 см, KN = 14 см. Найдите углы треугольника MNK, если ∠A = 80°, ∠B = 60°.
Правильный ответ: 80°, 60°, 40°.

№ 3. Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК||АС, ВМ : AM = 1 : 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см.
Правильный ответ: 5 см.

№ 4*. В трапеции ABCD (AD и ВС основание) диагонали пересекаются в точке О, AD = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника AOD равна 45 см².
Правильный ответ: 5 см².

Задания и Ответы на Вариант 2

№ 1. Дано: РЕ||NK, МР = 8, MN = 12, ME = 6 (рис. 7.55). Найти: а) МК; б) РЕ : NK; в) S_MPE : S_MNK.
Правильный ответ: а) 9; б) 2 : 3; в) 4 : 9.

№ 2. В ΔАВС АВ = 12 см, ВС = 18 см, ∠В = 70°, а в ΔMNK MN = 6 см, NK = 9 см, ∠N = 70°. Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, ∠K = 60°.
Правильный ответ: АС = 14 см, ∠C = 60°.

№ 3. Отрезки АВ и CD пересекаются в точке О так, что ∠ACO = ∠BDO, АО : ОВ = 2:3. Найдите периметр треугольника АСО, если периметр треугольника BOD равен 21 см.
Правильный ответ: 14 см.

№ 4*. В трапеции ABCD (AD и ВС основания) диагонали пересекаются в точке О, S_AOD= 32 см², S_BOC = 8 см². Найдите меньшее основание трапеции, если большее из них равно 10 см.
Правильный ответ: 5 см.

Нажмите на спойлер, чтобы увидеть решения заданий:

Смотреть указания к РЕШЕНИЮ заданий

Другие варианты контрольной № 3 в 8 классе:

К-3 Уровень 2 + Решения
К-3 Уровень 3 + Решения

Вы смотрели: Контрольная работа № 3 по геометрии в 8 классе с ответами УМК Атанасян Просвещение (Уровень 1-й) «Признаки подобия треугольников». Урок 38 поурочного планирования по геометрии. Геометрия 8 класс Контрольная работа 3 Уровень 1 (легкий).

Смотреть Список всех контрольных по геометрии в 8 классе УМК Атанасян.

В учебных целях использованы цитаты из учебного пособия «Поурочные разработки по геометрии. 8 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».

Вернуться к Списку уроков Тематического планирования в 8 классе.

Источник

Определение подобных треугольников.

Список вопросов теста

Вопрос 1

Варианты ответов

Вопрос 2

Варианты ответов

Вопрос 3

Варианты ответов

Вопрос 4

Варианты ответов

Вопрос 5

Варианты ответов

Вопрос 6

Треугольники KPF и ЕМТ подобны, причем КР : МЕ = PF : МТ = KF : ET, угол F = 30°, угол Е = 49°. Чему равен угол М?

Варианты ответов

Вопрос 7

Варианты ответов

Вопрос 8

Вопрос 9

Вопрос 10

Варианты ответов

1. Организационный момент

2. Выполнение контрольной работы

Контрольная работа по геометрии. I уровень сложности

Контрольная работа по геометрии. II уровень сложности

Контрольная работа по геометрии. III уровень сложности

3. Рефлексия учебной деятельности

Решения и ответы на контрольную работу I уровня сложности

Решения и ответы на контрольную работу II уровня сложности

Решения и ответы на контрольную работу III уровня сложности

Критерии оценивания результатов контрольной работы

Уровень 1 (легкий). Геометрия 8 класс

К-3 Уровень 1 Вариант 1

К-3 Уровень 1 Вариант 2

Геометрия 8 класс Контрольная работа 3 Решения и ответы (легкий уровень):

Задания и Ответы на Вариант 1

Задания и Ответы на Вариант 2

Другие крутые статьи на нашем сайте:

Контрольная работа по геометрии.
I уровень сложности

Контрольная работа по геометрии.
II уровень сложности

Контрольная работа по геометрии.
III уровень сложности

Решения и ответы на контрольную работу
I уровня сложности

Решения и ответы на контрольную работу
II уровня сложности

Решения и ответы на контрольную работу
III уровня сложности

Геометрия 8 класс Контрольная работа 3
Решения и ответы (легкий уровень):