Обычно для расчёта
параметров строится немасштабный
сетевой график, который после расчёта
может быть привязан к календарным датам
путём проставления их у каждого события
графика.
График, построенный
в масштабе времени, более удобен для
контроля за ходом выполнения работ.
Построение сетевого графика в масштабе
времени производят по ранним началам
или поздним окончаниям работ. Построение
масштабного сетевого графика (см.
рисунок 18) выполняется в следующей
последовательности:
Снизу или сверху
будущего графика вычерчивается
календарная линейка, на которой
указываются порядковые рабочие дни с
привязкой их к календарным датам
соответствующего месяца и года; все
работы изображаются в масштабе времени,
при этом начальное событие должно
располагаться в соответствии со
значением раннего начала работы, а
величина проекции работы на ось времени
принимается равной сумме её продолжительности
и частного резерва времени.
Сначала изображаются
работы, лежащие на критическом пути,
продолжительность которых определяет
срок строительства.
Затем по порядку
наносят остальные работы с частными
резервами времени. Продолжительность
работ изображают сплошной, а частный
резерв времени работы – пунктирной
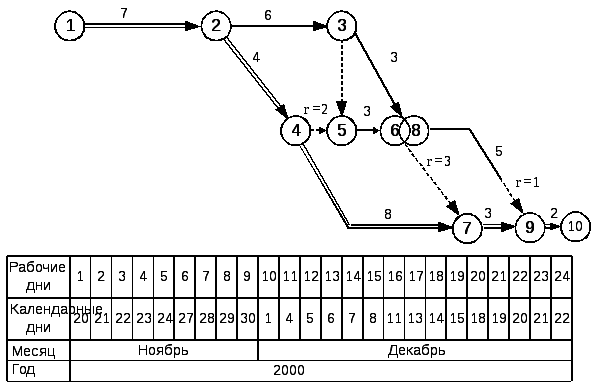
линией. Например, работа 8-9 (рисунок 18)
продолжительностью 5 дней и частным
резервом времени, равным одному дню,
наносится от центра события 8 до центра
события 9. Продолжительность работы
8-9, равная 5 дням, изображается сплошной
линией, а частный резерв (1 день) –
пунктирной. Продолжительность работ и
частных резервов времени указывают
цифрами над работами, а под работами –
их наименования.
Рисунок 18 — Сетевой график, построенный
в масштабе времени
По сетевому
графику, построенному в масштабе
времени, легко построить графики
потребности рабочих в смену или день,
для чего на сетевом графике рядом с
продолжительностью работ указывается
цифрами количество рабочих, выполняющих
данный процесс. График потребности
рабочих строится в произвольном
масштабе в виде диаграммы.
2.6. Оптимизация сетевых графиков по времени
Рассчитанный
сетевой график не всегда соответствует
заданному сроку, поэтому необходимо
проводить корректирование графика
с учётом существующих ограничений.
Процесс корректирования сетевых
графиков с целью выполнения поставленных
ограничений называется оптимизацией.
Существует несколько
видов оптимизации: по времени и по
равномерному потреблению ресурсов
(трудовых, материально-технических,
финансовых).
Оптимизация
сетевых графиков по времени производится
в случаях, если расчётный критический
путь оказался больше или меньше
нормативного. Если расчётный критический
путь меньше нормативного, возникает
дополнительный резерв времени, который
при оптимизации может быть использован
для увеличения продолжительности
отдельных видов работ (критических).
Если расчётный критический путь больше
нормативного, возникает отрицательный
резерв времени; в этом случае сетевая
модель пересматривается и сокращается
время выполнения работ, лежащих на
критическом пути. Сокращение
продолжительности работ достигается
пересмотром карточки-определителя
работ и ресурсов. Если продолжитель-ность
работы нужно сократить, то увеличивают
ресурсы, а если увеличить, необходимо
уменьшить ресурсы.
При проведении
оптимизации по времени рекомендуется
уменьшать или увеличивать
продолжительность не только критических
работ, но и работ, лежащих на
подкритических путях.
В результате
сокращения или увеличения продолжительности
работ получится новая сеть, требующая
проверки всех расчётных параметров
при сохранении ее топологии.
Оптимизацию
сетевых графиков по времени рассмотрим
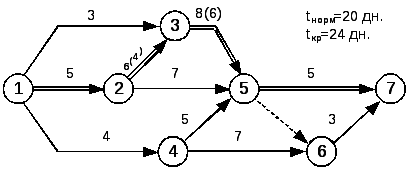
на примере (рисунок 19).
Рисунок 19 — Сетевой график
Продолжительность
критического пути определяем расчётом
ранних параметров работ. Данные
записываем в таблицу 4.
Т а б л и ц а 4 –
Расчет ранних параметров
|
i-j |
До оптимизации |
После |
||||||
|
ti-j |
|
|
|
ti-j |
|
|
|
|
|
1-2 |
5 |
0 |
5 |
0 |
5 |
0 |
5 |
0 |
|
1-3 |
3 |
0 |
3 |
8 |
3 |
0 |
3 |
6 |
|
1-4 |
4 |
0 |
4 |
0 |
4 |
0 |
4 |
0 |
|
2-3 |
6 |
5 |
11 |
0 |
4 |
5 |
9 |
0 |
|
2-5 |
7 |
5 |
12 |
7 |
7 |
5 |
12 |
3 |
|
3-5 |
8 |
11 |
19 |
0 |
6 |
9 |
15 |
0 |
|
4-5 |
5 |
4 |
9 |
10 |
5 |
4 |
9 |
6 |
|
4-6 |
7 |
4 |
11 |
8 |
7 |
4 |
11 |
4 |
|
5-6 |
0 |
19 |
19 |
0 |
0 |
15 |
15 |
0 |
|
5-7 |
5 |
19 |
24 |
0 |
5 |
15 |
20 |
0 |
|
6-7 |
3 |
19 |
22 |
2 |
3 |
15 |
18 |
2 |
|
Соб.7 |
24 |
tкр= |
∑r=35 |
tкр= |
∑r=21 |
Из расчёта видно,
что продолжительность критического
пути (tкр=
24) больше нормативной (tнорм=
20). Уменьшаем продолжительность
критических работ за счёт перераспределения
внутренних ресурсов, не меняя топологии
сети. Новые продолжительности работ
проставлены на графике (рисунок 19) в
скобках.
После изменения
продолжительности работ производим
повторный расчёт, из которого видно
(см. таблицу 4), что длина критического
пути равна нормативной. При необходимости
можно менять продолжительность работ
как на критических, так и подкритических
путях, тогда положение критического
пути может измениться.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Анализ сетевого графика
С помощью данной программы можно онлайн определить параметры сетевого графика (рассчитать сроки свершения событий, резервы времени и критический путь), найти коэффициенты напряженности. Оптимизация сетевого графика проводится по следующим критериям: число исполнителей, резервы-затраты, сокращение сроков (см. вкладку Параметры сетевого графика).
Сетевой график можно нарисовать, а также задать в виде матрицы или таблицы (меню Действия).
- Ввод данных
- Параметры сетевого графика
- Решение
- Видеоинструкция
- Оформление Word
Нумерация вершин с №1
Выберите нужный тип вершины и нажмите левой кнопкой мыши на графическом полотне
Размеры графического полотна
Ширина
Высота
Созданный сетевой график можно сохранить в форматах docx и png (меню Действия).
Далее можно найти параметры сетевой модели (критический путь, резервы времени, построить диаграмму Ганта и многое другое).
Для сформированного графа можно выполнить следующие действия:
Здесь будет показано решение
Инструкция к сервису
Для добавления вершины на графическое полотно необходимо использовать соответствующую фигуре кнопку Добавить. Новый объект также можно вставить, предварительно выделив его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле. Нумерация вершин может начинаться с 0, для этого нужно снять отметку с пункта Нумерация вершин с №1.
1234
1103015
Нумерация вершин с 0
0123
1103015
Чтобы соединить вершины, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить.
Сетевая модель может быть представлена в табличной форме и в виде матрицы весов (матрицы расстояний). Чтобы использовать данные представления, выберите меню Операции.
Построенный граф можно сохранить в формате docx или png.
Если в качестве формы вершин используется прямоугольник, то при построении секторальной диаграммы применяется методология Microsoft Visio с отображением параметров duration, ES, EF, LS, LF, and slack.
Основные определения
Ориентированный граф, в котором существует лишь одна вершина, не имеющая входящих дуг, и лишь одна вершина, не имеющая выходящих дуг, называется сетью. Сеть, моделирующая комплекс работ, называется его сетевой моделью или сетевым графиком. Дуги, соединяющие вершины графа, ориентированы в направлении достижения результата при осуществлении комплекса работ.
Наиболее распространен способ представления моделируемого комплекса работ в понятиях работ и событий.
Понятие «работа» имеет следующие значения:
- «действительная работа» – процесс, требующий затрат времени и ресурсов;
- «фиктивная работа» – логическая связь между двумя или несколькими работами, указывающая на то, что начало одной работы зависит от результатов другой. Фиктивная работа не требует затрат времени и ресурсов, продолжительность ее равна нулю.
Работа на графике изображается стрелкой, над которой указывается затрачиваемое на нее время. Длина стрелки и ее ориентация на графике не имеют значения. Желательно только выдерживать направление стрелок так, чтобы начальное событие для работы (обозначается i) располагалось слева в сетевом графике, а конечное (обозначается j) — справа. Для отображения фиктивных работ используют пунктирные стрелки, над которыми время не указывается или проставляется ноль.
На сетевой модели событиям соответствуют вершины графа.
Правила построения сетевой модели
Правило 1. Каждая операция в сети представляется одной и только одной дугой (стрелкой). Ни одна из операций не должна появляться в модели дважды. При этом следует различать случай, когда какая-либо операция разбивается на части; тогда каждая часть изображается отдельной дугой.
Правило 2. Ни одна пара операций не должна определяться одинаковыми начальным и конечным событиями. Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число операций допустимо выполнять одновременно.
Правило 3. При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы:
а) Какие операции необходимо завершить непосредственно перед началом рассматриваемой операции?
б) Какие операции должны непосредственно следовать после завершения данной операции?
в) Какие операции могут выполняться одновременно с рассматриваемой?
При построении сетевого графика следует соблюдать следующие правила:
- в сети не должно быть «тупиков», т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
- В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
- в сети не должно быть замкнутых контуров (рис.1);
- Любые два события должны быть непосредственно связаны не более чем одной работой.
- В сети рекомендуется иметь одно исходное и одно завершающее событие.
- Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.
Построение сетевого графика начинается с изображения начального события, которое обозначается цифрой 1 и обводится кружком. Из начального события выпускают стрелки, соответствующие работам, которым не предшествуют какие-либо другие работы. По определению, момент завершения работы является событием. Поэтому каждая стрелка
завершается кружком – событием, в котором проставляется номер этого события. Нумерация событий произвольная. На следующем этапе построения изображаем работы, которым предшествуют уже нарисованные работы (то есть которые опираются на уже построенные работы) и т. д. На следующем этапе отражаем логические взаимосвязи между работами и определяем конечное событие сетевого графика, на которое не опираются никакие работы. Построение закончено, далее необходимо провести упорядочение сетевого графика.
Методы оптимизации сетевого графика
Логико-математическое описание, формирование планов и управляющих воздействий осуществляется на базе использования особого класса моделей, называемых сетевыми моделями.
После построения и расчета сетевого графика (определения его параметров), выполнения анализа графика, заключающегося в оценке его целесообразности и структуры, оценке загрузки исполнителей, оценке вероятности наступления завершающего события в заданный срок, следует приступать к оптимизации сетевого графика. Процедура оптимизации заключается в приведение графика в соответствие с заданными сроками выполнения работ, возможностями подрядных организаций и т.д. В общем случае под оптимизацией следует понимать процесс улучшения организации выполнения работ.
Для возможности оптимизации сетевой модели, все исходные данные вводятся в виде таблицы (Операции/Добавить в виде таблицы).
- Оптимизация сетевой модели по критерию «число исполнителей». Заполняется столбец Количество исполнителей Ч
- Оптимизация сетевой модели по критерию «время – стоимость» (
время — затраты
). В случае известных коэффициентов затрат на ускорение работ заполняется только этот столбец h(i,j). Иначе, заполняются столбцы tопт (Нормальный режим), Минимальное время работ, tmin (Ускоренный режим), Нормальная стоимость, Cн и Срочная стоимость, Cc.
Графики привязки (а) и загрузки (b) до оптимизации
1,261,311,452,532,613,684,644,725,866,817,83 1122 3194175 6 7 8189 10 11 12 13 141315 16 17 181019 20 21 22423 24 25 26127
Графики привязки (а) и загрузки (b) после оптимизации
1,261,311,452,532,613,684,644,725,866,817,83 1122 3114145 6 7158 9 10 111812 13 14 151016 17 18419 20 21 221023 24 25 26727
Диаграмма Ганта
1,241,331,452,5112,6143,64,6174,75,8196,8277,825
Чтобы построить диаграмму Ганта по графику работ, необходимо выделить пункт Строить диаграмму Ганта
. Также можно создать график на основе введенных данных. Для этого следует указать количество работ (мероприятий) и даты их проведения.
Количество работ
Примеры сетевых моделей
Рассмотрим варианты сетевых графиков из кулинарной области на примере варки борща из курицы.
а) Варка в обычной посуде
12345
11030157
Работы:
1,2: чистка овощей (капуста, морковь, картофель, свекла, лук), 10 мин.
1,3: варить курицу, 30 мин.
2,3: положить капусту и варить 10 мин.
3,4: положить 1/2 свеклы, морковь и картофель. Варить 15 мин.
4,5: доложить остатки свеклы, лук, зелень. Варить 7 мин.
б) Варка в посуде с эффектом русской печи
(трехслойное дно, крышка без отверстий)
12345
1010203060
Работы:
1,2: чистка овощей (капуста, морковь, картофель, свекла, лук), 10 мин.
1,4: варить курицу в обычной посуде, 30 мин.
2,3: положить овощи в спецпосуду, добавить 3 ложки воды, нагреть до T=70 C и выключить, 10 мин.
3,4: приготовление овощей в собственном соку, 20 мин.
4,5: добавить к курице приготовленные овощи. Настаивается 60 мин.
Список литературы
- Мушик Э., Мюллер П. Методы принятия технических решений. Пер. с нем. –М.: Мир, 1990.
- Таха Х. Введение в исследование операций. В 2-х книгах. Кн. 2. Пер. с англ. –М.: мир, 1985.
- Управление в системах РАВ: Учебник. –Л.: Воениздат, 1980.
Текст
РазмерЦвет
Линия
ТолщинаЦвет
пунктирная — — — —
Размеры в px и фон
wh
Текст (вес)
РазмерЦвет
Линия
ТолщинаЦвет
пунктирная — — —
концевой маркер →
Тип
Число строк
Минимальное время работ, tmin
Максимальное время работ, tmax
Количество исполнителей, чел., Ч
Коэффициент затрат на ускорение работ, руб./сут., h(i,j)
Нормальная стоимость, Cн
Срочная стоимость, Cc
По умолчанию минимальное количество заполняемых столбцов равно трем: i, j, tопт. Чтобы иметь возможность ввести и другие данные, выделите соответствующий пункт.
В каждой строке укажите вершины в формате:v1-v2:n, например1-2:4
1-3:8
2-4:12
4-1:6
Выберите номер критического пути.
Файл «тема 3. сетевые модели управления проектами» внутри архива находится в папке «Лекции». Документ из архива «Лекции»,
который расположен в категории «».
Всё это находится в предмете «проектная деятельность» из 1 семестр, которые можно найти в файловом архиве НИУ «МЭИ» .
Не смотря на прямую связь этого архива с НИУ «МЭИ» , его также можно найти и в других разделах. .
Рис.. Сетевой график производства монтажных работ
Решение 1.4. Для оптимизации графика методом перераспределения ресурсов переставим одну бригаду с работы (50,70) на работу (40,60) (рис. ). В результате перевода людей изменится продолжительность выполнения работ и общая продолжительность выполнения сетевого графика в целом.

Рис.. Оптимизация сетевого графика методом
перераспределения ресурсов
Для оптимизации сетевого графика с изменением сети и без привлечения дополнительных ресурсов увеличим степень совмещения работ за счет введения поточной организации работ на критическом пути. Результаты представлены на рис.

Рис. Оптимизация сетевого графика поточным методом
Для оптимизации сетевого графика можно использовать и параллельное выстраивание выполнения критических работ (рис.)

Рис. Оптимизация сетевого графика параллельным методом
Оптимизация сетевого графика без изменения сети с привлечением дополнительных ресурсов представлена на рис.

Рис. Оптимизация сетевого графика методом привлечения
дополнительных ресурсов
2.3. Оптимизация сетевого графика по ресурсам на основе построения сети в масштабе времени
Целью оптимизации может быть составление расписания работ, при котором все работы будут обеспечены ресурсами в условиях, когда имеются ограничения по ресурсу.
Ресурсы делятся на ненакапливаемые и накапливаемые (хранимые, складируемые). Минимизируя интенсивности потребления ресурса, следует добиться, чтобы максимальное значение ресурса было минимальным (сглаживание эпюры потребности в ресурсе).
Ограничения записываются в виде следующих неравенств:
а) в случае ненакапливаемого ресурса
qij ≤ p
где qij — суммарная интенсивность потребления ресурса параллельно выполняемых работ ; p — заданная интенсивность поступления ресурса;
б) в случае накапливаемого ресурса
Qij ≤ Qзав – Qзап,
где Qij – суммарный расход ресурса с начала выполнения комплекса на заданный момент времени; Qзап – запас ресурса на заданный момент времени, обеспечивающий непрерывность работ при заданных параметрах поставок (объём, частота); Qзав – объём материала, завезённого на площадку на заданный момент времени с начала завоза.
Оптимизация по этим видам ресурса осуществляется одними и теми же методами. Разница заключается лишь в том, что в случае ненакапливаемого ресурса применяется график интенсивности расхода (поступления) ресурса, а в случае накапливаемого ресурса – графики (интегральные) завоза и расхода ресурса.
Методы оптимизации можно разделить на:
-
оптимизацию сетевой модели с помощью сетевого графика, построенного в масштабе времени (масштабного графика) по ранним (поздним) срокам свершения событий;
-
оптимизацию сетевой модели с помощью сетевого графика, построенного в виде линейной диаграммы.
Оптимизация масштабного графика делится на оптимизацию графика, построенного по ранним срокам свершения событий, и оптимизацию графика, построенного по поздним срокам свершения событий.
Порядок построения сетевого графика в масштабе времени:
-
выбрать разновидность графика (по ранним срокам наступления событий или по поздним срокам);
-
рассчитать ранние (поздние) сроки наступления событий;
-
выбрать масштаб времени;
-
на поле графика нанести события в соответствии с их ранними (поздними) сроками;
-
соединить события работами;
-
на стрелках (дугах) отметить (выделить) работы, считая первоначально, что все они начинаются в ранние сроки, при этом горизонтальная проекция работы должна быть равна продолжительности работы в выбранном масштабе времени ( T lg = T ij + R ij ).
Дуги будут состоять из двух частей: собственно работа (показывается жирно) и свободный резерв времени (показывается тонкой линией).
Задача 1.5. Постройте сетевой график организации работ в масштабе времени (рис.). Выполните оптимизацию по ресурсам.
Решение 1.5. При проведении оптимизации масштабного графика по ресурсу следует придерживаться следующего порядка операций:
-
рассчитать ранние (поздние) сроки наступления событий;
-
построить масштабный график, принимая во внимание, что события совершаются в свои ранние (поздние) сроки;
-
построить эпюру интенсивности потребления ресурса и, если ресурс накапливаемый, интегральную эпюру потребления ресурса;
-
наложить на эпюру интенсивности потребления ненакапливаемого ресурса ограничение (постоянное или переменное во времени). В случае накапливаемого ресурса наложить на интегральную эпюру потребления ресурса интегральную эпюру его завоза;
-
используя свободные резервы времени работ, устранить превышение интенсивности потребления ресурса над ограничением.
С этой целью работы могут быть сдвинуты частично или полностью на величину резерва времени, растянуты (увеличена продолжительность) частично или полностью на величину свободного резерва времени, сдвинуты и растянуты одновременно, при этом суммарная потребность в резерве для этих целей не должна превышать полного его значения (рис. ).
Рис.. Сетевой график производства работ в масштабе времени
Рис. . Результаты оптимизации сетевого графика и диаграмма движения ресурсов
2.4. Оптимизация сетевого графика, построенного в виде линейной диаграммы
Оптимизация графика, построенного в линейной форме, имеет некоторые особенности по сравнению с графиком, построенным в масштабе времени.
Порядок оптимизации можно представить в следующей последовательности:
-
Подготовительный этап:
-
рассчитать полные резервы времени работ;
-
построить сетевой график в виде линейной диаграммы;
-
построить эпюру интенсивности потребления ресурса;
-
наложить на полученный график интенсивности поступления ресурса ограничения;
-
сделать вывод о необходимости оптимизации, если q ij > p ; если Qij > Qзав – Qзап или если q ij min и Q ij min.
-
Основной этап. Оптимизация в соответствии с заданным ограничением.
Задача 1.6. Постройте сетевой график в виде линейной диаграммы (см. рис. 39). Постройте график движения рабочей силы и проведите оптимизацию по ресурсам.
Решение 1.6. Построим сетевой график производства работ в линейном виде. При построении линейной диаграммы на рисунок наносят координатные оси. При этом ось Х принимается за ось времени, а ось У принимается за ось работ. На оси У через равный интервал времени указываются работы, длительность которых равна периоду между ранним сроком начала работы и ранним сроком окончания работы (рис. ).
Для проведения оптимизации сетевого графика на основе линейной диаграммы рассчитаем полные резервы времени работ и запишем их в квадратиках над соответствующими работами.
Для удобства расчетов этапы работы по оптимизации графика сведем в табл.
Ранжирование работ производится в порядке увеличения полного резерва времени, а в случае равенства его величины в порядке уменьшения ресурса. При проведении расчетов работы разрывать нельзя. Если работа началась, то она должна быть закончена без перерыва.
Оптимизация выполняется по участкам слева направо.
Рис. Сетевой график, построенный в виде линейной диаграммы
Таблица
Оптимизация участка графика от T = 0 до T = 2
|
Код работ (i,j) |
Полный резерв времени (Rпij) |
Ресурс (Pij) |
Начинается/ продолжается (Н/П) |
Ранг |
Оставить /удалить (+/–) |
|
1,2 |
28 |
3 |
Н |
5 |
+ |
|
1,3 |
24 |
6 |
Н |
4 |
– |
|
1,4 |
0 |
7 |
Н |
1 |
+ |
|
1,5 |
22 |
4 |
Н |
3 |
+ |
|
1,7 |
10 |
6 |
Н |
2 |
+ |
|
Σpij = 26 > N = 20 |
S1=P1,4 + P1, 7=7–6=13<N=20. Работы 1,4 и 1,7 остаются в этом участке.
S2=S1+P1, 5=13+4=17<20. Работа 1,5 остаётся в этом участке.
S3=S2+P1, 3=17+6=23>20. Начало работы 1,3 сдвигается на правую границу данного участка (убирается из данного участка).
S4=S3+P1, 2=17+3=20=N. Работа 1,2 остаётся в этом участке.
Таблица
Оптимизация участка графика от T=2 до T=4
|
Код работ (i,j) |
Полный резерв времени (Rпij) |
Ресурс (Pij) |
Начинается/ продолжается (Н/П) |
Ранг |
Оставить /удалить (+/–) |
|
1,2 |
28 |
3 |
П |
0 |
+ |
|
1,3 |
22 |
6 |
Н |
1 |
+ |
|
1,4 |
0 |
7 |
П |
0 |
+ |
|
1,5 |
22 |
4 |
П |
0 |
+ |
|
Σpij = 20 = N = 20 |
Таблица
Оптимизация участка графика от T = 4 до T = 8
|
Код работ (i,j) |
Полный резерв времени (Rпij) |
Ресурс (Pij) |
Начинается/ продолжается (Н/П) |
Ранг |
Оставить /удалить (+/–) |
|
1,3 |
22 |
6 |
Н |
1 |
+ |
|
1,4 |
0 |
7 |
П |
0 |
+ |
|
1,5 |
22 |
4 |
П |
0 |
+ |
|
Σpij = 17 < N = 20 |
Таблица
Оптимизация участка графика от T = 8 до T = 10
|
Код работ (i,j) |
Полный резерв времени (Rпij) |
Ресурс (Pij) |
Начинается/ продолжается (Н/П) |
Ранг |
Оставить /удалить (+/–) |
|
1,4 |
0 |
7 |
П |
0 |
+ |
|
1,5 |
22 |
4 |
П |
0 |
+ |
|
3,6 |
26 |
6 |
Н |
2 |
+ |
|
3,8 |
22 |
10 |
Н |
1 |
– |
|
Σpij = 27 > N = 20 |
S0=7+4=11<N=20.
S1=S0+P3,8=11+10=21>N=20. Начало работы 3,8 сдвигается на правую границу данного участка.