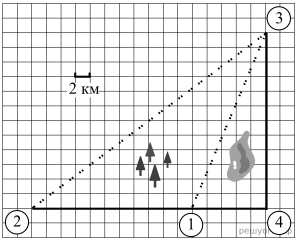
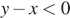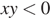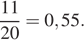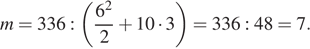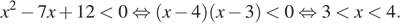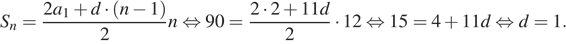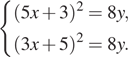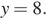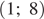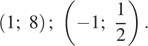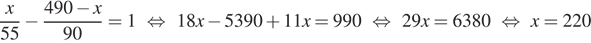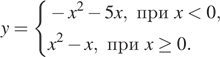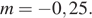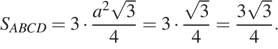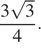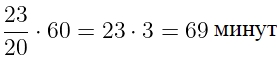Сколько километров проедут Гена с дедушкой, если они поедут по шоссе через деревню Кулаки?
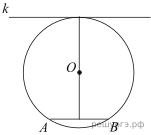
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
1
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
| Населённые пункты | Кулаки | Илькино | Осинки | Кудрино |
|---|---|---|---|---|
| Цифры |
2
Найдите расстояние от деревни Осинки до села Кудрино по прямой. Ответ выразите в километрах.
3
Сколько времени затратят на дорогу Гена с дедушкой, если они поедут сначала до Илькино, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.
4
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гена с дедушкой, если поедут этим маршрутом.
Спрятать решение
Решение.
Расстояние, которое проедут Гена с дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Ответ: 56.
ОГЭ математика
133 вариант
1. Пользуясь описанием, определите, какими цифрами на плане
обозначены населённые пункты. В ответе запишите полученную последовательность
четырёх цифр.
|
Населённые |
Кулаки |
Илькино |
Осинки |
Кудрино |
|
Цифры |
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они
собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно
проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через
деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево
на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно
свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой
дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов,
сторона каждой клетки равна 2 км.
2. Найдите расстояние от деревни Осинки до села Кудрино по прямой.
Ответ выразите в километрах.
3. Сколько километров проедут Гена с дедушкой, если они поедут по
шоссе через деревню Кулаки?
4. Сколько времени затратят на дорогу Гена с дедушкой, если они
поедут сначала до Илькино, а затем свернут на грунтовую дорогу, идущую мимо
озера? Ответ выразите в минутах.
5. Определите, на какой маршрут потребуется меньше всего времени. В
ответе укажите, сколько минут потратят на дорогу Гена с дедушкой, если поедут
этим маршрутом.
6.
Найдите значение выражения 3,8 + 2,9.
7. Одна из точек, отмеченных на координатной прямой, соответствует
числу . Какая это точка?
1) M
2) N
3) P
4) Q
8. Найдите значение выражения
9. Найдите корни уравнения
Если
корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. На экзамене 60 билетов, Стас не выучил 6 из них. Найдите
вероятность того, что ему попадется выученный билет.
11. Установите соответствие между функциями и их графиками.
Графики
Функции
Запишите в ответ цифры, расположив их в порядке, соответствующем
буквам:
12. Зная длину своего шага, человек может приближённо подсчитать
пройденное им расстояние s по формуле s = nl,
где n — число шагов, l — длина шага. Какое
расстояние прошёл человек, если l = 80 см, n =1600
? Ответ выразите в километрах.
13. На каком рисунке изображено множество решений неравенства ?
|
1) |
2) |
|
3) |
4) |
14. В фирме «Родник» стоимость (в рублях) колодца из железобетонных
колец рассчитывается по формуле , где
n — число колец, установленных при рытье колодца. Пользуясь этой формулой,
рассчитайте стоимость колодца из 5 колец.
15.
В треугольнике ABC угол C равен
133°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
16.
Сторона равностороннего треугольника равна Найдите
радиус окружности, описанной около этого треугольника.
17.
Высота равнобедренной трапеции, проведённая из вершины C,
делит основание AD на отрезки длиной 1 и 5. Найдите длину
основания BC.
18.
На клетчатой бумаге с размером клетки 1х1 изображён
треугольник . Найдите длину его средней линии,
параллельной стороне .
19. Какое из следующих утверждений верно?
1) В прямоугольном треугольнике гипотенуза равна сумме катетов.
2) Всегда один из двух смежных углов острый, а другой тупой.
3) Через любую точку, лежащую вне окружности, можно провести две
касательные к этой окружности.
В
ответ запишите номер выбранного утверждения.
20. Решите неравенство
21. Первую половину пути автомобиль проехал со скоростью 90 км/ч, а
вторую — со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на
протяжении всего пути.
22. Постройте график функции и
определите, при каких значениях m прямая y = m имеет
с графиком ровно одну общую точку.
23. Прямая, параллельная основаниям и
трапеции
,
проходит через точку пересечения диагоналей трапеции и пересекает её боковые
стороны и
в точках
и
соответственно.
Найдите длину отрезка , если
см,
см.
24. Окружности с центрами в точках I и J пересекаются
в точках A и B, причём точки I и J лежат
по одну сторону от прямой AB. Докажите, что AB⊥IJ.
25. Из вершины прямого угла C треугольника ABC проведена
высота CP. Радиус окружности, вписанной в треугольник BCP,
равен 8, тангенс угла BAC равен . Найдите радиус вписанной
окружности треугольника ABC.
Решение
1. Пользуясь описанием, определите, какими цифрами на плане
обозначены населённые пункты. В ответе запишите полученную последовательность
четырёх цифр.
|
Населённые |
Кулаки |
Илькино |
Осинки |
Кудрино |
|
Цифры |
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они
собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно
проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через
деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево
на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно
свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой
дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов,
сторона каждой клетки равна 2 км.
Решение.
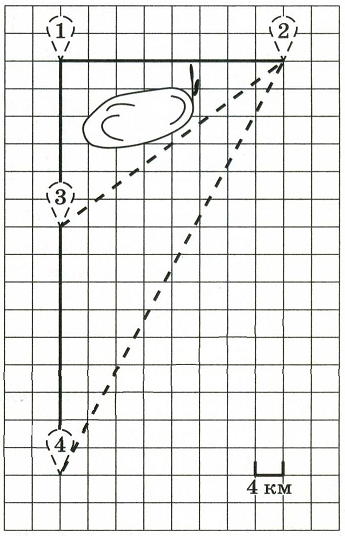
Пользуясь описанием и рисунком можно заметить, что деревня Кулаки
соответствует цифре 4, деревня Илькино — цифре 1, деревня Осинки — цифре 2 и
деревня Кудрино —цифре 3.
Ответ: 4123.
2. Найдите расстояние от деревни Осинки до села Кудрино по прямой.
Ответ выразите в километрах.
Решение.
Расстояние от деревни Осинки до села Кудрино соответствует длине
гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме Пифагора
имеем:
Ответ: 40.
3. Сколько километров проедут Гена с дедушкой, если они поедут по
шоссе через деревню Кулаки?
Решение.
Расстояние, которое проедут Гена с дедушкой, проезжая через
Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и
24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Ответ: 56.
4. Сколько времени затратят на дорогу Гена с дедушкой, если они
поедут сначала до Илькино, а затем свернут на грунтовую дорогу, идущую мимо
озера? Ответ выразите в минутах.
Решение.
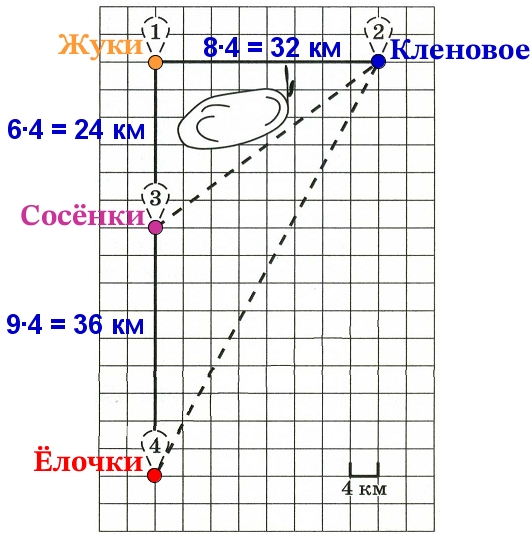
По шоссе Гена с дедушкой проедут 22 километра со скоростью 60
км/ч. Следовательно, они затратят 22 : 60 = 0,37 часа или 22 минуты. Дальше по
условию задачи они свернут на грунтовую дорогу длина которой равна длине
гипотенузы прямоугольного треугольника с катетами 24 и 10. Таким образом, по
теореме Пифагора длина составит:
По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч,
следовательно они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61
минута.
Ответ: 61.
5. Определите, на какой маршрут потребуется меньше всего времени. В
ответе укажите, сколько минут потратят на дорогу Гена с дедушкой, если поедут
этим маршрутом.
Решение.
Гена с дедушкой могут поехать тремя разными маршрутами. Рассмотрим
каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути соответствует
длине гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме
Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 40 км/ч дедушка с Геной
потратят 40 : 40 = 1 час или 60 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По
шоссе Гена с дедушкой проедут 22 километра со скоростью 60 км/ч. Следовательно,
они затратят часа
или 22 минуты. Дальше по условию задачи они свернут на грунтовую дорогу длина
которой равна длине гипотенузы прямоугольного треугольника с катетами 24 и 10.
Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч,
следовательно они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61
минута.
3) По шоссе через Кулаки. Расстояние, которое проедут Гена с
дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного
треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние
равно 32 + 24 = 56.
Двигаясь по шоссе со скоростью 60 км/ч, Гена с дедушкой
потратят часа
или 56 минут.
Таким образом, самый быстрый путь составит 56 минут.
Ответ: 56.
6.
Найдите значение выражения 3,8 + 2,9.
Решение.
Найдем значение выражения: 3,8 + 2,9 = 6,7.
Ответ: 6,7.
7. Одна из точек, отмеченных на координатной прямой, соответствует
числу . Какая это точка?
1) M
2) N
3) P
4) Q
Решение.
Чтобы ответить на вопрос, возведём в квадрат числа 5, 6, 7:
Число 37 лежит между 36 и 49 и ближе всех находится к числу 36.
Значит, соответствует
точке P.
Правильный ответ указан под номером 3.
8. Найдите значение выражения
Решение.
Найдем значение выражения:
Ответ: 7.
9. Найдите корни уравнения
Если
корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение.
Перенесём всё в уравнении в одну сторону:
По теореме, обратной теореме Виета, сумма корней равна 8, а их
произведение равно 7. Тем самым, это числа 1 и 7.
Ответ: 17.
10. На экзамене 60 билетов, Стас не выучил 6 из них. Найдите вероятность
того, что ему попадется выученный билет.
Решение.
Стас выучил 60 − 6 = 54 билета, значит, вероятность того, что ему
попадется один из них равна
Ответ: 0,9.
11. Установите соответствие между функциями и их графиками.
Графики
Функции
Запишите в ответ цифры, расположив их в порядке, соответствующем
буквам:
Решение.
Все представленные здесь функции — гиперболы. Общая формула для
уравнения гиперболы: ,
если , то ветви гиперболы располагаются в первой и третьей
четвертях, в противном случае — во второй и четвёртой четвертях.
Для того, чтобы отличить гиперболы лежащие в одинаковых четвертях
нужно подставить какое-нибудь значение в формулу и
проверить, какому графику будет соответствовать полученное значение.
Таким образом, установим соответсвие: А — 4, Б — 1, В — 3.
Ответ: 413.
12. Зная длину своего шага, человек может приближённо подсчитать
пройденное им расстояние s по формуле s = nl,
где n — число шагов, l — длина шага. Какое
расстояние прошёл человек, если l = 80 см, n =1600
? Ответ выразите в километрах.
Решение.
Найдём какое расстояние прошёл человек, подставим длину шага и
число шагов в формулу:
Ответ:1,28.
13. На каком рисунке изображено множество решений неравенства ?
|
1) |
2) |
|
3) |
4) |
Решение.
Решим неравенство:
Ответ: 1.
14. В фирме «Родник» стоимость (в рублях) колодца из железобетонных
колец рассчитывается по формуле , где
n — число колец, установленных при рытье колодца. Пользуясь этой формулой,
рассчитайте стоимость колодца из 5 колец.
Решение.
Подставим в формулу значение переменной :
Ответ: 26500.
15.
В треугольнике ABC угол C равен
133°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение.
Внешний угол треугольника является смежным с , а
значит,
Ответ: 47.
16.
Сторона равностороннего треугольника равна Найдите
радиус окружности, описанной около этого треугольника.
Решение.
Треугольник ABC правильный, значит, все его углы
равны по 60°. По теореме синусов: значит
Ответ: 2.
17.
Высота равнобедренной трапеции, проведённая из вершины C,
делит основание AD на отрезки длиной 1 и 5. Найдите длину
основания BC.
Решение.
Проведём вторую высоту и введём обозначения, как показано на
рисунке. Рассмотрим треугольники и
они
прямоугольные, равно
равно
следовательно,
эти треугольники равны, откуда Найдём отрезок
Высоты
и
перпендикулярны
значит,
они параллельны, равно
следовательно,
—
прямоугольник, поэтому
Ответ: 4.
18.
На клетчатой бумаге с размером клетки 1х1 изображён
треугольник . Найдите длину его средней линии,
параллельной стороне .
Решение.
Из рисунка видно, что длина стороны равна 10. Длина
средней линии равна половине длины стороны , следовательно, 5.
Ответ: 5
19. Какое из следующих утверждений верно?
1) В прямоугольном треугольнике гипотенуза равна сумме катетов.
2) Всегда один из двух смежных углов острый, а другой тупой.
3) Через любую точку, лежащую вне окружности, можно провести две
касательные к этой окружности.
В
ответ запишите номер выбранного утверждения.
Решение.
Рассмотрим каждое из утверждений:
1) «В прямоугольном треугольнике гипотенуза равна сумме катетов»
— неверно, по теореме Пифагора в прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов.
2) «Всегда один из двух смежных углов острый, а другой тупой»
— неверно, так как сумма смежных углов равна 180°, следовательно,
если один из углов прямой, то смежный ему будет тоже прямой.
3) «Через любую точку, лежащую вне окружности, можно провести две касательные
к этой окружности» — верно по свойству окружности.
Ответ: 3.
20. Решите неравенство
Решение.
Последовательно получаем:
Произведение двух множителей меньше нуля тогда и только тогда,
когда знаки множителей различны, следовательно:
Ответ: [-1; 1].
21. Первую половину пути автомобиль проехал со скоростью 90 км/ч, а
вторую — со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на
протяжении всего пути.
Решение.
Пусть половина трассы составляет s километров. Тогда
первую половину трассы автомобиль проехал за часа, а вторую — за
часа. Значит, его средняя
скорость в км/ч равна
Ответ: 99 км/ч.
22. Постройте график функции и
определите, при каких значениях m прямая y = m имеет
с графиком ровно одну общую точку.
Решение.
Значение выражения неотрицательно
при и
а при
и
значение этого выражения отрицательно. Построим
график функции при
и
и график
функции при
и
Прямая y
= m имеет с графиком ровно одну общую точку при m = 1
и m = −1.
23. Прямая, параллельная основаниям и
трапеции
,
проходит через точку пересечения диагоналей трапеции и пересекает её боковые
стороны и
в точках
и
соответственно.
Найдите длину отрезка , если
см,
см.
Решение.
1) по двум углам:
а) как
вертикальные;
б) как внутренние
накрест лежащие углы при и секущей
.
2) по двум углам:
а) — общий;
б) как
соответственные при и секущей
.
см.
3) Аналогично см.
4) см.
Ответ: 30 см.
24. Окружности с центрами в точках I и J пересекаются
в точках A и B, причём точки I и J лежат
по одну сторону от прямой AB. Докажите, что AB⊥IJ.
Решение.

медиану треугольника
Стороны
и
равны
как радиусы окружности, поэтому треугольник — равнобедренный,
следовательно, медиана является также высотой. Проведём
медиану Стороны
и
равны
как радиусы окружности, поэтому треугольник — равнобедренный,
следовательно, медиана является также высотой. Прямые
и
перпендикулярны
одной и той же прямой , следовательно, они параллельны. Эти
прямые проходят через одну и ту же точку значит, они
совпадают. Таким образом прямая перпендикулярна прямой
25. Из вершины прямого угла C треугольника ABC проведена
высота CP. Радиус окружности, вписанной в треугольник BCP,
равен 8, тангенс угла BAC равен . Найдите радиус вписанной
окружности треугольника ABC.
Решение.
Угол BAC равен углу BCP так
как и
. Так как тангенс это отношение
противолежащего катета к прилежащему, имеем: Тогда
а гипотенуза
по теореме
Пифагора. Площадь треугольника равна произведению половины его периметра на
радиус вписанной окружности, но площадь прямоугольного треугольника равна
половине произведения катетов, имеем:
Таким образом, а
Так
как то
а
по
теореме Пифагора.
В треугольнике площадь равна произведению половины
его периметра на радиус вписанной в него окружности, но площадь прямоугольного
треугольника равна половине произведения катетов, имеем:
Ответ:
Вариант № 6
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
|
Населённые пункты |
Кулаки |
Илькино |
Осинки |
Кудрино |
|
Цифры |
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
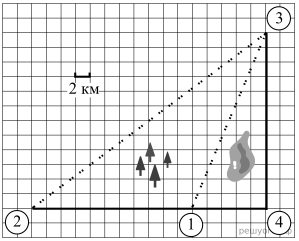
Решение. Пользуясь описанием и рисунком можно заметить, что деревня Кулаки соответствует цифре 4, деревня Илькино — цифре 1, деревня Осинки — цифре 2 и деревня Кудрино —цифре 3.
Ответ: 4123.
2. Найдите расстояние от деревни Осинки до села Кудрино по прямой. Ответ выразите в километрах.
Решение. Расстояние от деревни Осинки до села Кудрино соответствует длине гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме Пифагора имеем:
Ответ: 40.
3. Сколько километров проедут Гена с дедушкой, если они поедут по шоссе через деревню Кулаки?
Решение. Расстояние, которое проедут Гена с дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Ответ: 56.
4. Сколько времени затратят на дорогу Гена с дедушкой, если они поедут сначала до Илькино, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.
Решение. По шоссе Гена с дедушкой проедут 22 километра со скоростью 60 км/ч. Следовательно, они затратят 22 : 60 = 0,37 часа или 22 минуты. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 24 и 10. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч, следовательно, они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61 минута.
Ответ: 61.
5. Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гена с дедушкой, если поедут этим маршрутом.
Решение. Гена с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути соответствует длине гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 40 км/ч дедушка с Геной потратят 40 : 40 = 1 час или 60 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Гена с дедушкой проедут 22 километра со скоростью 60 км/ч. Следовательно, они затратят часа или 22 минуты. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 24 и 10. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч, следовательно, они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61 минута.
3) По шоссе через Кулаки. Расстояние, которое проедут Гена с дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Двигаясь по шоссе со скоростью 60 км/ч, Гена с дедушкой потратят часа или 56 минут.
Таким образом, самый быстрый путь составит 56 минут.
Ответ: 56.
6. Найдите значение выражения
Решение. Последовательно получаем:
Ответ: −720.
7. Известно, что . Какое из указанных утверждений верно?
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Решение. По условию оба числа положительны и Рассмотрим все варианты ответа:
1) — неверно, так как
и
2) — неверно, так как по условию
3) — неверно, так как по условию
4) — верно.
Правильный ответ указан под номером 4.
8. Найдите значение выражения
Решение. Вычислим:
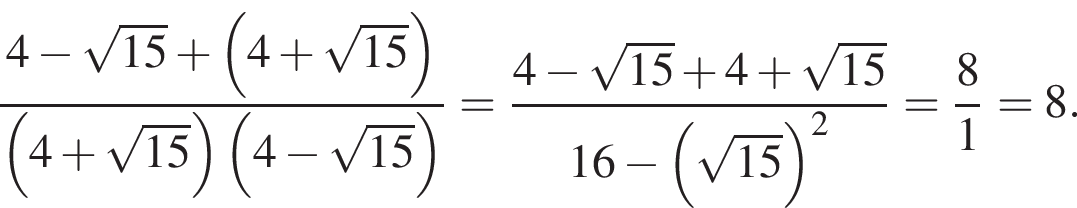
Ответ: 8.
9. Решите уравнение: x2 − 25 = 0.
Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Решение. Решим уравнение:
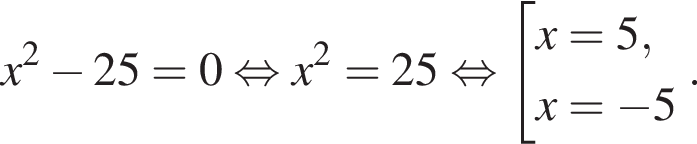
Ответ: 5.
10. У бабушки 15 чашек: 9 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Решение. Вероятность того, что чай нальют в чашку с синими цветами равна отношению количества чашек с синими цветами к общему количеству чашек. Всего чашек с синими цветами: Поэтому искомая вероятность
Ответ: 0,4.
11. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
КОЭФФИЦИЕНТЫ
А)
Б)
В)
ГРАФИКИ
|
1)
|
2)
|
3)
|
В таблице под каждой буквой укажите соответствующий номер.
|
А |
Б |
В |
Решение. Если парабола задана уравнением , то: при
то ветви параболы направлены вверх, а при
— вниз. Значение c соответствует значению функции в точке x = 0. Следовательно, если график пересекает ось ординат выше оси абсцисс, то значение c положительно, если ниже оси абсцисс — отрицательно.
Таким образом, функциям соответствуют следующие графики: А — 1, Б — 2, В — 3.
Ответ: 123.
12. Площадь треугольника можно вычислить по формуле , где
— длины сторон треугольника, r — радиус вписанной окружности. Вычислите длину стороны c, если
.
Решение. Подставим в формулу известные значения величин:
Ответ: 10.
13. Укажите решение неравенства
1)
2)
3)
4)
Решение. Решим неравенство:
Решению неравенства соответствует третий вариант ответа.
Правильный ответ указан под номером 3.
14. Три конькобежца, скорости которых в некотором порядке образуют геометрическую прогрессию, одновременно стартуют (из одного места) по кругу. Через некоторое время второй конькобежец обгоняет первого, пробежав на 400 метров больше его. Третий конькобежец пробегает то расстояние, который пробежал первый к моменту обгона его вторым, за время на мин больше, чем первый. Найдите скорость первого конькобежца в м/мин.
Решение. Из условия видно, что скорость 2-го конькобежца наибольшая, а 3-го — наименьшая. Обозначим за b скорость третьего конькобежца.
|
скорость (м/мин) |
|
|
1-й конькобежец |
qb |
|
2-й конькобежец |
q2b |
|
3-й конькобежец |
b |
Где q 1, b 0, t — время, за которое второй обгоняет первого.
Составим систему уравнений:

Разделим (1) на (2): м/мин — скорость первого конькобежца.
Ответ: 600 м/мин.
15.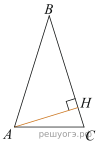
В треугольнике ABC AB = BC, а высота AH делит сторону BC на отрезки BH = 45 и CH = 30. Найдите cosB.
Решение. Из треугольника ABH, по определению косинуса:
Ответ: 0,6.
16. 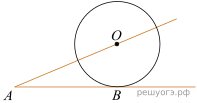
Решение. Соединим отрезком точки O и B; полученный отрезок — радиус, проведённый в точку касания, поэтому OB перпендикулярен AB. Задача сводится к нахождению катета OB прямоугольного треугольника AOB: по теореме Пифагора равен 6 см.
Ответ: 6.
17. 
.
Решение. Площадь треугольника равна половине произведения сторон на синус угла между ними. Так как угол равностороннего треугольника равен 60° и все стороны равны 10, имеем:
Ответ: 25.
18. 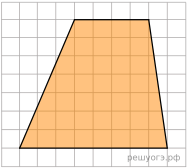
Решение. 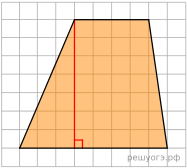
Ответ: 42
19. Какие из следующих утверждений верны?
1. Площадь треугольника меньше произведения двух его сторон.
2. Средняя линия трапеции равна сумме её оснований.
3. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Решение. Рассмотрим каждое из утверждений:
1. Площадь треугольника меньше произведения двух его сторон — верно, согласно формуле для площади треугольника:
2. Средняя линия трапеции равна сумме её оснований — неверно, средняя линия трапеция равна полусумме её оснований
3. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны — верно, согласно признаку подобия треугольников.
Ответ: 13
20. Решите систему уравнений 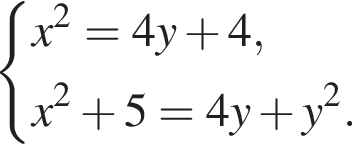
Решение. Последовательно получаем:
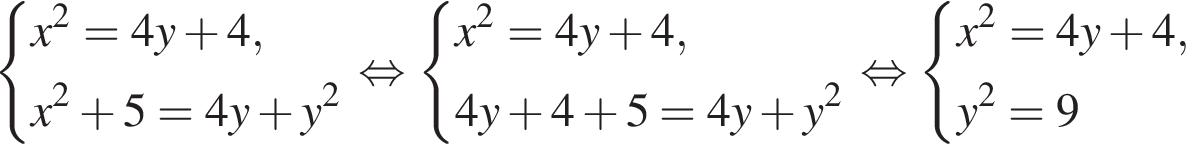
При y = −3 первое уравнение не имеет решений. При y = 3 получаем:
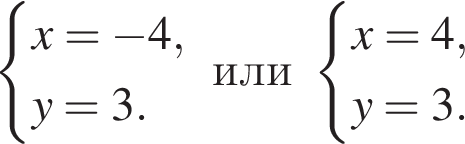
Ответ: (−4; 3); (4; 3).
21. Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Решение. Пусть скорость второго велосипедиста равна ,
тогда скорость первого велосипедиста равна
Составим таблицу по данным задачи:
|
Скорость, км/ч |
Время, ч |
Расстояние, км |
|
|
Первый велосипедист |
|
|
60 |
|
Второй велосипедист |
x |
|
60 |
Так как первый прибыл к финишу на 3 ч. раньше второго, то можно составить следующее уравнение:
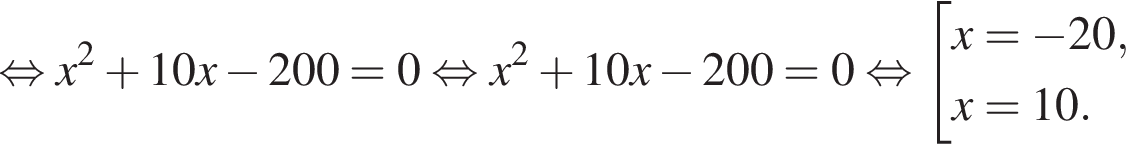
По условию задачи нам подходят только положительные корни, поэтому скорость второго велосипедиста равна
Ответ: 10.
22. При каком значении р прямая имеет с параболой
ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении
Решение. Найдём абсциссы точек пересечения:
Графики функций, будут иметь ровно одну точку пересечения, если это уравнение имеет ровно одно решение. То есть, если дискриминант этого квадратного уравнения будет равен нулю.
Подставив параметр p в уравнение, найдём x координату точки пересечения этих функций:
Координата y находится путём подстановки координаты x в любое из уравнений, например, в первое:
Теперь, зная p, можем построить графики обеих функций (см. рис.).
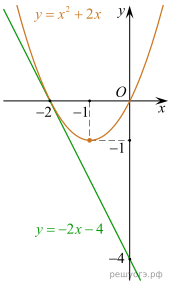
Ответ: p = −4; координаты искомой точки: (−2; 0).
23. 
Решение. 
Ответ: 50.
24. 
Решение. 
25. В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 15 , BC = 14.
Решение. 
Поскольку QD = AD − AQ = AD − BC = 1, получаем, что
Из подобия треугольников TBC и TAD находим, что TC = 14x.
Поэтому
Следовательно,
Ответ:
|
№ задания |
ответ |
|
1 |
4123 |
|
2 |
40 |
|
3 |
56 |
|
4 |
61 |
|
5 |
56 |
|
6 |
−720 |
|
7 |
4 |
|
8 |
8 |
|
9 |
5 |
|
10 |
0,4 |
|
11 |
123 |
|
12 |
10 |
|
13 |
3 |
|
14 |
600 |
|
15 |
0,6 |
|
16 |
6 |
|
17 |
25 |
|
18 |
42 |
|
19 |
13 |
|
20 |
(−4; 3); (4; 3). |
|
21 |
10 |
|
22 |
p = −4; координаты искомой точки: (−2; 0). |
|
23 |
50 |
|
24 |
— |
|
25 |
|
Домашнее задание по алгебре на 17.05.2021
1. Задание 1
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
| Населённые пункты | Кулаки | Илькино | Осинки | Кудрино |
| Цифры |
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
Пользуясь описанием и рисунком можно заметить, что деревня Кулаки соответствует цифре 4, деревня Илькино — цифре 1, деревня Осинки — цифре 2 и деревня Кудрино —цифре 3.
Ответ: 4123.
Ответ: 4123
2. Задание 2
Найдите расстояние от деревни Осинки до села Кудрино по прямой. Ответ выразите в километрах.
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
Расстояние от деревни Осинки до села Кудрино соответствует длине гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме Пифагора имеем:
Ответ: 40.
Ответ: 40
3. Задание 3
Сколько километров проедут Гена с дедушкой, если они поедут по шоссе через деревню Кулаки?
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
Расстояние, которое проедут Гена с дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Ответ: 56.
Ответ: 56
4. Задание 4
Сколько времени затратят на дорогу Гена с дедушкой, если они поедут сначала до Илькино, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
По шоссе Гена с дедушкой проедут 22 километра со скоростью 60 км/ч. Следовательно, они затратят 22 : 60 = 0,37 часа или 22 минуты. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 24 и 10. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч, следовательно они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61 минута.
Ответ: 61.
Ответ: 61
5. Задание 5
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гена с дедушкой, если поедут этим маршрутом.
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
Гена с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути соответствует длине гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 40 км/ч дедушка с Геной потратят 40 : 40 = 1 час или 60 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Гена с дедушкой проедут 22 километра со скоростью 60 км/ч. Следовательно, они затратят 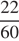
По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч, следовательно они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61 минута.
3) По шоссе через Кулаки. Расстояние, которое проедут Гена с дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Двигаясь по шоссе со скоростью 60 км/ч, Гена с дедушкой потратят 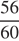
Таким образом, самый быстрый путь составит 56 минут.
Ответ: 56.
Ответ: 56
6. Задание 6
Найдите значение выражения 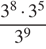
Решение.
Найдем значение выражения:
Ответ: 81.
Ответ: 81
7. Задание 7
На координатной прямой отмечены числа x и y.
Какое из приведённых утверждений неверно?
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Решение.
Заметим, что 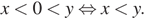
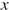
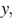
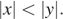
1) 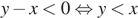
2) 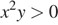
3) 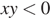
4) 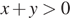
Ответ указан под номером: 1.
Ответ: 1
8. Задание 8
Упростите выражение 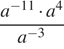

Решение.
Упростим выражение:
При 
Ответ: 16.
Ответ: 16
9. Задание 9
Решите уравнение 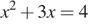
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение.
Запишем уравнение в виде 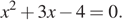
Тем самым это числа −4 и 1.
Ответ: −41.
Ответ: -41
-41
10. Задание 10
Родительский комитет закупил 20 пазлов для подарков детям в связи с окончанием учебного года, из них 11 с машинами и 9 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Илюша. Найдите вероятность того, что Илюше достанется пазл с машиной.
Решение.
Вероятность того, что Коле достанется пазл с машиной равна
Ответ: 0,55.
Ответ: 0,55
0,55
11. Задание 11
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке [2; +∞)
2) f( −1 ) < f( 5 )
3) Наименьшее значение функции равно −9
Решение.
Проверим каждое утверждение.
1) На луче [2; +∞) большему значению аргумента сответствует большее значение функции. Следовательно, функция возрастает на этом луче; первое утверждение верно.
2) Значения фунцкии в точках −1 и 5 равны нулю, поэтому f(−1) = f(5). Второе утверждение неверно.
3) Наименьшее значение функции равно −9. Третье утверждение верно.
Ответ: 2.
Ответ: 2
12. Задание 12
Полную механическую энергию тела (в джоулях) можно вычислить по формуле 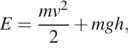
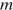
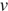
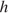
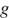
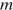

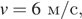
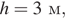
Решение.
Выразим массу: 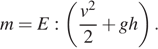
Ответ: 7.
Ответ: 7
13. Задание 13
На каком рисунке изображено множество решений неравенства 
Решение.
Решим неравенство:
Ответ: 3.
Ответ: 3
14. Задание 14
Грузовик перевозит партию щебня массой 90 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 2 тонны щебня. Определите, сколько тонн щебня было перевезено за десятый день, если вся работа была выполнена за 12 дней.
Решение.
Пусть в первый день грузовик перевез 
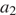
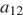

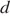
Имеем:
Следовательно, за десятый день было перевезено 11 тонн щебня.
Ответ: 11.
Ответ: 11
15. Задание 15
Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах.
Решение.
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании. Поскольку трапеция является равнобедренной, углы при основании равны. Значит, каждый из них равен 110°. Сумма односторонних углов трапеции равна 180°, поэтому меньший угол равен 180° − 110° = 70°.
Ответ: 70.
Ответ: 70
16. Задание 16
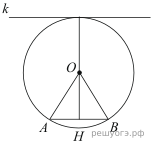
Радиус окружности с центром в точке O равен 65, длина хорды AB равна 66 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Решение.
Проведём построение и введём обозначения, как показано на рисунке. Рассмотрим треугольники 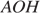
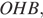
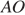
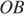
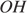

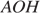
Следовательно, расстояние от хорды до параллельной ей касательной равно 56 + 65 = 121.
Ответ: 121.
Ответ: 121
17. Задание 17
В ромбе сторона равна 10, одна из диагоналей — 10, а угол, лежащий напротив этой диагонали, равен 60°. Найдите площадь ромба, деленную на 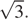
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
Ответ: 50.
Ответ: 50
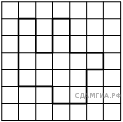
18. Задание 18
На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
Решение.
Площадь данной фигуры равна выделенным клеткам. Посчитаем клетки — их 15. Таким образом, площадь равна 15.
Ответ: 15.
Ответ: 15
19. Задание 19
Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Если угол острый, то смежный с ним угол также является острым» — неверно, т. к. смежные углы в сумме составляют 180°.
2) «Диагонали квадрата взаимно перпендикулярны» — верно, т. к. квадрат — частный случай ромба.
3) «В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности» — верно, т. к. окружность — это множество точек, находящихся на заданном расстоянии от данной точки.
Ответ: 23.
Ответ: 23
20. Задание 20
Решите систему уравнений
Решение.
Правые части уравнений системы равны, значит,
откуда 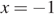
При 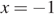
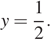

Решения системы уравнений: 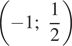
Ответ:
Критерии проверки:
21. Задание 21
Расстояние между городами А и В равно 490 км. Из города А в город В со скоростью 55 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 90 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
Решение.
Пусть 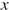

Составим таблицу по данным задачи:
Так как второй автомобиль вышел на 1 ч. позже первого, составим уравнение:
Ответ: 220 км.
Другое решение:
За первый час пути автомобиль, выехавший из города А, проехал 55 километров и расстояние от него до города В стало равным 435 км. Далее, скорость сближения двух автомобилей равна 145 км/ч, значит, они встретятся через 3 часа после выезда второго автомобиля. Таким образом, первый автомобиль до встречи находился в пути 4 часа, и проехал за это время 220 километров.
Ответ: 220 км.
Критерии проверки:
220 км.
22. Задание 22
Постройте график функции 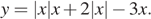
Решение.
Раскрывая модуль, получим, что функцию можно представить следующим образом:
Этот график изображён на рисунке:
Из графика видно, что прямая 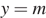
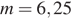
Ответ: −0,25; 6,25.
Критерии проверки:
−0,25; 6,25.
23. Задание 23
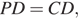
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
Решение.
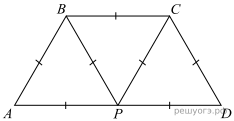
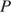
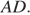
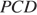
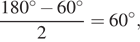

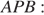
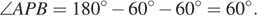
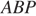
Ответ:
Критерии проверки:
24. Задание 24
В окружности с центром 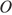

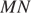
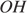
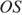
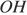
Решение.
Проведем ОK, ON, OL, OM — радиусы. Треугольники KOL и MON равны по трем сторонам, тогда высоты OH и OS также равны как элементы равных треугольников. Что и требовалось доказать.
Критерии проверки:
25. Задание 25
В треугольнике 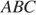
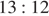

Марина летом отдыхает у дедушки в деревне Ивановки. В пятницу они
собираются съездить на машине в село Гавриловка. Из Ивановки
в Гавриловку можно проехать по прямой грунтовой дороге. Есть более
длинный путь по шоссе — через деревню Пересыпкино до деревни
Ольшанка, где нужно повернуть под прямым углом направо на другое шоссе,
ведущее в Гавриловку. Есть и третий маршрут: в Пересыпкине можно
свернуть на прямую грунтовую дорогу, которая идёт мимо пруда прямо
в Гавриловку.
По шоссе Марина с дедушкой едут со скоростью 48 км/ч, а по грунтовой
дороге — 25 км/ч. На плане изображено взаимное расположение населённых
пунктов, сторона каждой клетки равна 1 км.
Пользуясь описанием, определите, какими цифрами на плане обозначены
населённые пункты. В ответе запишите полученную последовательность
четырёх цифр.
Населённые
пункты Гавриловка Пересыпкино Ольшанка Ивановка
Цифры
Математика, 06.03.2019 16:30, аврсчрм
Сдробями( три разных ) 1)напишите десятичную дробь а)с четырьмя знаками после запятой, равную 0,87 в)с пятью знаками после запятой равную 0,541 с)с тремя знаками после запятой равную 35 д)с двумя знаками после запятой равную 8,40000
2)запишите короче дроби : 2,5000 ; 3,02000 ; 20,010 3)приписав справа нули уровняйте число знаков после запятой в десятичных дробях : 1,8 ; 13,54 и 0,789
Ответов: 4
Посмотреть
Версия для печати и копирования в MS Word
1
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
| Населённые пункты | Новомальцево | Парахино | Александровка | Фомино |
|---|---|---|---|---|
| Цифры |
Показать
1
Найдите расстояние от деревни Александровки до села Фомино по прямой. Ответ выразите в километрах.
2
Сколько километров проедут Настя с дедушкой, если они поедут по шоссе через Парахино?
3
Сколько времени затратят на дорогу Настя с дедушкой, если они поедут сначала до Новомальцево, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.
4
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Настя с дедушкой, если поедут этим маршрутом.
2
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
| Населённые пункты | Кулаки | Илькино | Осинки | Кудрино |
|---|---|---|---|---|
| Цифры |
Показать
1
Найдите расстояние от деревни Осинки до села Кудрино по прямой. Ответ выразите в километрах.
2
Сколько километров проедут Гена с дедушкой, если они поедут по шоссе через деревню Кулаки?
3
Сколько времени затратят на дорогу Гена с дедушкой, если они поедут сначала до Илькино, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.
4
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гена с дедушкой, если поедут этим маршрутом.
3
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
| Населённые пункты | Гавриловка | Пересыпкино | Ольшанка | Ивановка |
|---|---|---|---|---|
| Цифры |
Показать
1
Найдите расстояние от деревни Ивановки до села Гавриловка по прямой. Ответ выразите в километрах.
2
Сколько километров проедут Марина с дедушкой, если они поедут по шоссе через деревню Ольшанку?
3
Сколько времени затратят на дорогу Марина с дедушкой, если они поедут сначала до Пересыпкино, а затем свернут на грунтовую дорогу, идущую мимо пруда? Ответ выразите в минутах.
4
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Марина с дедушкой, если поедут этим маршрутом.
По какой дороге ехать быстрей? Задача из ОГЭ
Как и всегда, необходимо по тексту задания ответить на пять вопросов.
Юля летом отдыхает у дедушки и бабушки в деревне Царёво. Юля с дедушкой собираются съездить на машине на железнодорожную станцию Таировку. Из Царёво в Таировку можно проехать по шоссе до деревни Ключи, где нужно свернуть под прямым углом налево на другое шоссе, ведущее в Таировку через посёлок Демидово. Из Царёво в Таировку можно проехать через посёлок Демидово и не заезжая в Ключи, но тогда первую часть пути надо будет ехать по прямой лесной дороге. Есть и третий маршрут: доехать по прямой грунтовой дороге мимо озера до села Федяево и там, повернув направо, по шоссе добраться до Таировки.
По шоссе Юля с дедушкой едут со скоростью 60 км/ч, а по лесной и грунтовой дорогам — 45 км/ч. Расстояние по шоссе от Царёво до Ключей равно 72 км, от Таировки до Ключей — 60 км, от Таировки до Демидово — 30 км, а от Таировки до Федяево — 27 км.
Задание 1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность пяти цифр.
| Насел. пункты | п. Демидово | д. Ключи | ст. Таировка | с. Федяево | д. Царёво |
| Цифры |
Решение.
В тексте задания сказано, что из Царёво в Таировку можно проехать по шоссе до деревни Ключи, где нужно свернуть под прямым углом налево на другое шоссе, ведущее в Таировку через посёлок Демидово. Значит, 3 – Демидово, 4 – Ключи, 1 – Таировка, 5 – Царево. Также указано, что есть и третий маршрут: доехать по прямой грунтовой дороге мимо озера до села Федяево. Получаем, 2 – Федяево.
Ответ: 34125
Задание 2. Найдите расстояние от деревни Царёво до посёлка Демидово по лесной дороге. Ответ дайте в километрах.
Решение.
Отметим на карте все населенные пункты и расстояния между ними.
Расстояние от деревни Царёво до посёлка Демидово по лесной дороге – это гипотенуза прямоугольного треугольника с катетами 72 и 60-30 = 30 км. Следовательно, длина проселочной дороги, равна:
км
Ответ: 78
Задание 3. Сколько минут затратят на дорогу Юля с дедушкой, если поедут на станцию через Ключи?
Ниже сделаем схему движения Юли и дедушки по шоссе. Из теста задачи, мы знаем, что скорость движения по шоссе равна 60 км/ч. Красными цифрами вынесено расстояние между поселками.
Решение.
Пусть на станцию через Ключи равен
S = 72+60 = 132 км
Движение по шоссе идет со скоростью v=60 км/ч. Получаем время в пути (в минутах):
Ответ: 132 минуты.
Задание 4. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Юля с дедушкой, если поедут этим маршрутом.
Решение.
По шоссе Юля с дедушкой едут со скоростью 60 км/ч, а по лесной и грунтовой дорогам — 45 км/ч. До Таировки можно добраться тремя маршрутами:
1. По шоссе через Ключи 72+60 = 132 км. Время в пути (в минутах) составит:
минуты
2. По грунтовой дороги до Демидово (78 км, см. задача 2) и по шоссе 30 км:
минуты
3. По грунтовой дороге до Федяево ( км) и по шоссе 27 км:
минут.
Наименьшее время составляет 127 минут.
Ответ: 127
Задание 5. На шоссе машина дедушки расходует 6,5 литра бензина на 100 км. Известно, что на путь из Царёво до Таировки через Ключи и на путь через Федяево ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на грунтовых дорогах?
Решение.
Обозначим расход бензина на грунтовых дорогах через x. Тогда можно записать равенство:
Ответ: 9,1
* * * * *
Задача про маршруты №2 для ОГЭ
Территория, находящаяся внутри кольцевой линии, называется Центральным городским районом. Найдите его площадь S (в км2), если длина кольцевой ветки равна 40 км. В ответе укажите значение выражения S π.
На рисунке изображена схема метро города N. Станция Ветреная расположена между станциями Центральная и Дальняя. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя, Птичья и Весёлая. Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звёздная. Всего в метрополитене города N есть три станции, от которых тоннель ведёт только в одну сторону — это станции Дальняя, Верхняя и Звёздная. Антон живёт недалеко от станции Надежда.
Решение.
Сначала найдём радиус окружности:
Теперь найдём площадь:
Таким образом, получаем ответ:
Ответ: 400.
* * * * *
Задача №3: Найдите площадь (в км2), которую занимает заказник.
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.
Решение.
Площадь заказника равна:
Ответ: 351.
* * * * *
Задача №4 по математике про маршрут
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гриша с дедушкой, если поедут этим маршрутом.
Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село Бережки.
По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге —50 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
Гриша с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути равна длине гипотенузы прямоугольного треугольника с катетами 30 и 16. По теореме Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 50 км/ч дедушка с Гришой потратят 34 : 50 = 0,68 часа или 40,8 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Гриша с дедушкой проедут 18 километров со скоростью 60 км/ч. Следовательно, они затратят 18 : 60 = 0,3 часа или 18 минут. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 12 и 16. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Гриша с дедушкой едут со скоростью 50 км/ч, следовательно, они затратят 20 : 50 = 0,4 часа или 24 минуты.
Таким образом, Гриша с дедушкой на весь путь затратят 24 + 18 = 42 минуты.
3) По шоссе через Афонино. Расстояние, которое проедут Гриша с дедушкой, проезжая через Афонино, равно сумме длин катетов прямоугольного треугольника с катетами 30 и 16. Таким образом, имеем, что искомое расстояние равно 30 + 16 = 46.
Двигаясь по шоссе со скоростью 60 км/ч Гриша с дедушкой потратят 46 : 60 часа или 46 минут.
Таким образом, самый быстрый путь составит 40,8 минут.
Ответ: 40,8.
* * * * *
Задача №5 для экзамена на тему дороги
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гена с дедушкой, если поедут этим маршрутом.
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
Гена с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути соответствует длине гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 40 км/ч дедушка с Геной потратят 40 : 40 = 1 час или 60 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Гена с дедушкой проедут 22 километра со скоростью 60 км/ч. Следовательно, они затратят часа или 22 минуты. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 24 и 10. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч, следовательно, они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61 минута.
3) По шоссе через Кулаки. Расстояние, которое проедут Гена с дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Двигаясь по шоссе со скоростью 60 км/ч, Гена с дедушкой потратят часа или 56 минут.
Таким образом, самый быстрый путь составит 56 минут.
Ответ: 56.
* * * * *
Задача №6 на тему определения маршрута
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Марина с дедушкой, если поедут этим маршрутом.
Марина летом отдыхает у дедушки в деревне Ивановки. В пятницу они собираются съездить на машине в село Гавриловка. Из Ивановки в Гавриловку можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Пересыпкино до деревни Ольшанка, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Гавриловку. Есть и третий маршрут: в Пересыпкине можно свернуть на прямую грунтовую дорогу, которая идёт мимо пруда прямо в Гавриловку.
По шоссе Марина с дедушкой едут со скоростью 48 км/ч, а по грунтовой дороге — 25 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 1 км.
Решение.
Марина с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути соответствует длине гипотенузы прямоугольного треугольника с катетами 15 и 20. По теореме Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 25 км/ч, дедушка с Мариной потратят 25 : 25 = 1 час или 60 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Марина с дедушкой проедут 12 километров со скоростью 48 км/ч. Следовательно, они затратят 12 : 48 = 0,25 часа или 15 минут. Дальше по условию задачи они свернут на грунтовую дорогу, длина которой равна длине гипотенузы прямоугольного треугольника с катетами 8 и 15. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Марина с дедушкой едут со скоростью 25 км/ч, следовательно, они затратят 17 : 25 = 0,68 часа или 40,8 минут.
Таким образом, Марина с дедушкой на весь путь затратят 15 + 40,8 = 55,8 минут.
3) По шоссе через Ольшанку. Расстояние, которое проедут Марина с дедушкой, проезжая через Ольшанку, равно сумме длин катетов прямоугольного треугольника с катетами 15 и 20. Таким образом, искомое расстояние равно 15 + 20 = 35.
Двигаясь по шоссе со скоростью 48 км/ч, Марина с дедушкой потратят 35 : 48 60 = 43,75 минут.
Таким образом, самый быстрый путь составит 43,75 минут.
Ответ: 43,75.
* * * * *
Задача №7 по математике про время движения по дороге
За какое наименьшее количество минут Таня с дедушкой могут добраться из Егорки в Жилино?
На рисунке изображён план сельской местности.
Таня на летних каникулах приезжает в гости к дедушке в деревню Антоновка (на плане обозначена цифрой 1). В конце каникул дедушка на машине собирается отвезти Таню на автобусную станцию, которая находится в деревне Богданово. Из Антоновки в Богданово можно проехать по просёлочной дороге мимо реки. Есть другой путь — по шоссе до деревни Ванютино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Богданово. Третий маршрут проходит по просёлочной дороге мимо пруда до деревни Горюново, где можно свернуть на шоссе до Богданово. Четвёртый маршрут пролегает по шоссе до деревни Доломино, от Доломино до Горюново по просёлочной дороге мимо конюшни и от Горюново до Богданово по шоссе. Ещё один маршрут проходит по шоссе до деревни Егорка, по просёлочной дороге мимо конюшни от Егорки до Жилино и по шоссе от Жилино до Богданово.
Шоссе и просёлочные дороги образуют прямоугольные треугольники.
По шоссе Таня с дедушкой едут со скоростью 50 км/ч, а по просёлочным дорогам — со скоростью 30 км/ч. Расстояние от Антоновки до Доломино равно 12 км, от Доломино до Егорки — 4 км, от Егорки до Ванютино — 12 км, от Горюново до Ванютино — 15 км, от Ванютино до Жилино — 9 км, а от Жилино до Богданово — 12 км.
Решение.
Рассчитаем время маршрута по прямой из деревни Егорки в деревню Жилино по проселочной местности и время маршрута из деревни Егорки в деревню Жилино по шоссе через деревню Ванютино. Расстояние от Егорки до Жилино соответствует гипотенузе треугольника с катетами 12 км и 9 км. По теореме Пифагора имеем: км. Следовательно, этот путь Таня с дедушкой проедут за
часа или 30 минут.
Расстояние от Егорки до Ванютино 12 км, от Ванютино до Жилино 9 км. Следовательно, этот путь Таня с дедушкой пройдут за часа или 25,2 минуты. Таким образом, наименьшее количество времени Таня с дедушкой затратят на путь из деревни Егорки в деревню Жилино по шоссе через деревню Ванютино — 25,2 минуты.
Ответ: 25,2.
* * * * *
Задача №8 для ОГЭ про определение расстояния
Найдите расстояние от Антоновки до Егорки по шоссе. Ответ дайте в километрах.
На рисунке изображён план сельской местности.
Таня на летних каникулах приезжает в гости к дедушке в деревню Антоновка (на плане обозначена цифрой 1). В конце каникул дедушка на машине собирается отвезти Таню на автобусную станцию, которая находится в деревне Богданово. Из Антоновки в Богданово можно проехать по просёлочной дороге мимо реки. Есть другой путь — по шоссе до деревни Ванютино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Богданово. Третий маршрут проходит по просёлочной дороге мимо пруда до деревни Горюново, где можно свернуть на шоссе до Богданово. Четвёртый маршрут пролегает по шоссе до деревни Доломино, от Доломино до Горюново по просёлочной дороге мимо конюшни и от Горюново до Богданово по шоссе. Ещё один маршрут проходит по шоссе до деревни Егорка, по просёлочной дороге мимо конюшни от Егорки до Жилино и по шоссе от Жилино до Богданово.
Шоссе и просёлочные дороги образуют прямоугольные треугольники.
По шоссе Таня с дедушкой едут со скоростью 50 км/ч, а по просёлочным дорогам — со скоростью 30 км/ч. Расстояние от Антоновки до Доломино равно 12 км, от Доломино до Егорки — 4 км, от Егорки до Ванютино — 12 км, от Горюново до Ванютино — 15 км, от Ванютино до Жилино — 9 км, а от Жилино до Богданово — 12 км.
Решение.
Расстояние от Антоновки до Доломино состоит из расстояний от Антоновки до Егорки и от Егорки до Доломино, следовательно, расстояние от Антоновки до Егорки равно км.
Ответ: 8.
* * * * *
Задача №9 по математике — найти расстояние
Найдите расстояние от Егорки до Жилино по прямой. Ответ дайте в километрах.
На рисунке изображён план сельской местности.
Таня на летних каникулах приезжает в гости к дедушке в деревню Антоновка (на плане обозначена цифрой 1). В конце каникул дедушка на машине собирается отвезти Таню на автобусную станцию, которая находится в деревне Богданово. Из Антоновки в Богданово можно проехать по просёлочной дороге мимо реки. Есть другой путь — по шоссе до деревни Ванютино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Богданово. Третий маршрут проходит по просёлочной дороге мимо пруда до деревни Горюново, где можно свернуть на шоссе до Богданово. Четвёртый маршрут пролегает по шоссе до деревни Доломино, от Доломино до Горюново по просёлочной дороге мимо конюшни и от Горюново до Богданово по шоссе. Ещё один маршрут проходит по шоссе до деревни Егорка, по просёлочной дороге мимо конюшни от Егорки до Жилино и по шоссе от Жилино до Богданово.
Шоссе и просёлочные дороги образуют прямоугольные треугольники.
По шоссе Таня с дедушкой едут со скоростью 50 км/ч, а по просёлочным дорогам — со скоростью 30 км/ч. Расстояние от Антоновки до Доломино равно 12 км, от Доломино до Егорки — 4 км, от Егорки до Ванютино — 12 км, от Горюново до Ванютино — 15 км, от Ванютино до Жилино — 9 км, а от Жилино до Богданово — 12 км.
Решение.
Расстояние от Егорки до Жилино соответствует гипотенузе прямоугольного треугольника с катетами 12 км и 9 км. По теореме Пифагора (км.)
Ответ: 15.
* * * * *
Задача №10 про чай во время поездки
Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.
Решение.
Найдём, сколько пакетиков чая ребята потратят за две недели:
Значит, им понадобится
пачек чая.
Таким образом, ребята должны купить 14 пачек чая.
Ответ: 14.
* * * * *
Задача №11 для экзамена на определение расстояния
Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.
Решение.
Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:
км.
Ответ: 30.
* * * * *
Задача №12 про маршрут поездки
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
| Населённые пункты: | Новомальцево | Парахино | Александровка | Фомино |
|---|---|---|---|---|
| Цифры |
Настя летом отдыхает у дедушки в деревне Александровке. В воскресенье они собираются съездить на машине в село Фомино. Из Александровки в Фомино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Новомальцево до деревни Парахино, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Фомино. Есть и третий маршрут: в Новомальцева можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Фомино.
По шоссе Настя с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 50 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 3 км.
Решение.
Пользуясь описанием и рисунком можно заметить, что деревня Новомальцево соответствует цифре 3, деревня Парахино — цифре 4, деревня Александровка — цифре 2 и деревня Фомино —цифре 1.
Ответ: 3421.
* * * * *
Задача №13 про маршрут Насти и дедушки
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Настя с дедушкой, если поедут этим маршрутом.
Настя летом отдыхает у дедушки в деревне Александровке. В воскресенье они собираются съездить на машине в село Фомино. Из Александровки в Фомино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Новомальцево до деревни Парахино, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Фомино. Есть и третий маршрут: в Новомальцева можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Фомино.
По шоссе Настя с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 50 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 3 км.
Решение.
Настя с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути соответствует длине гипотенузы прямоугольного треугольника с катетами 36 и 27. По теореме Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 50 км/ч дедушка с Настей потратят 45 : 50 = 0,9 часа или 54 минуты.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Настя с дедушкой проедут 12 километров со скоростью 60 км/ч. Следовательно, они затратят 12 : 60 = 0,2 часа или 12 минут. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 36 и 15. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Настя с дедушкой едут со скоростью 50 км/ч, следовательно, они затратят 39 : 50 = 0,78 часа или 46,8 минут.
Таким образом, Настя с дедушкой на весь путь затратят 46,8 + 12 = 58,8 минут.
3) По шоссе через Парахино. Расстояние, которое проедут Настя с дедушкой, проезжая через Парахино, равно сумме длин катетов прямоугольного треугольника с катетами 36 и 27. Таким образом, имеем, что искомое расстояние равно 36 + 27 = 63.
Двигаясь по шоссе со скоростью 60 км/ч Настя с дедушкой потратят 63 : 60 ≈ 1,05 часа или 63 минуты.
Таким образом, самый быстрый путь составит 54 минуты.
Ответ: 54.
* * * * *
Задача №14 ОГЭ про маршрут Гены и дедушки
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гена с дедушкой, если поедут этим маршрутом.
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
Гена с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути соответствует длине гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 40 км/ч дедушка с Геной потратят 40 : 40 = 1 час или 60 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Гена с дедушкой проедут 22 километра со скоростью 60 км/ч. Следовательно, они затратят часа или 22 минуты. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 24 и 10. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч, следовательно, они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61 минута.
3) По шоссе через Кулаки. Расстояние, которое проедут Гена с дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Двигаясь по шоссе со скоростью 60 км/ч, Гена с дедушкой потратят часа или 56 минут.
Таким образом, самый быстрый путь составит 56 минут.
Ответ: 56.
* * * * *
Задача №15 по математике на маршрут в деревню
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Марина с дедушкой, если поедут этим маршрутом.
Марина летом отдыхает у дедушки в деревне Ивановки. В пятницу они собираются съездить на машине в село Гавриловка. Из Ивановки в Гавриловку можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Пересыпкино до деревни Ольшанка, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Гавриловку. Есть и третий маршрут: в Пересыпкине можно свернуть на прямую грунтовую дорогу, которая идёт мимо пруда прямо в Гавриловку.
По шоссе Марина с дедушкой едут со скоростью 48 км/ч, а по грунтовой дороге — 25 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 1 км.
Решение.
Марина с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути соответствует длине гипотенузы прямоугольного треугольника с катетами 15 и 20. По теореме Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 25 км/ч, дедушка с Мариной потратят 25 : 25 = 1 час или 60 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Марина с дедушкой проедут 12 километров со скоростью 48 км/ч. Следовательно, они затратят 12 : 48 = 0,25 часа или 15 минут. Дальше по условию задачи они свернут на грунтовую дорогу, длина которой равна длине гипотенузы прямоугольного треугольника с катетами 8 и 15. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Марина с дедушкой едут со скоростью 25 км/ч, следовательно, они затратят 17 : 25 = 0,68 часа или 40,8 минут.
Таким образом, Марина с дедушкой на весь путь затратят 15 + 40,8 = 55,8 минут.
3) По шоссе через Ольшанку. Расстояние, которое проедут Марина с дедушкой, проезжая через Ольшанку, равно сумме длин катетов прямоугольного треугольника с катетами 15 и 20. Таким образом, искомое расстояние равно 15 + 20 = 35.
Двигаясь по шоссе со скоростью 48 км/ч, Марина с дедушкой потратят 35 : 48 60 = 43,75 минут.
Таким образом, самый быстрый путь составит 43,75 минут.
Ответ: 43,75.
* * * * *
Задача №16 для ОГЭ по определению маршрута дороги
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гриша с дедушкой, если поедут этим маршрутом.
Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село Бережки.
По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге —50 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
Гриша с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути равна длине гипотенузы прямоугольного треугольника с катетами 30 и 16. По теореме Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 50 км/ч дедушка с Гришой потратят 34 : 50 = 0,68 часа или 40,8 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Гриша с дедушкой проедут 18 километров со скоростью 60 км/ч. Следовательно, они затратят 18 : 60 = 0,3 часа или 18 минут. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 12 и 16. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Гриша с дедушкой едут со скоростью 50 км/ч, следовательно, они затратят 20 : 50 = 0,4 часа или 24 минуты.
Таким образом, Гриша с дедушкой на весь путь затратят 24 + 18 = 42 минуты.
3) По шоссе через Афонино. Расстояние, которое проедут Гриша с дедушкой, проезжая через Афонино, равно сумме длин катетов прямоугольного треугольника с катетами 30 и 16. Таким образом, имеем, что искомое расстояние равно 30 + 16 = 46.
Двигаясь по шоссе со скоростью 60 км/ч Гриша с дедушкой потратят 46 : 60 часа или 46 минут.
Таким образом, самый быстрый путь составит 40,8 минут.
Ответ: 40,8.
* * * * *
Задача №17 на определение времени маршрута
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Настя с дедушкой, если поедут этим маршрутом.
Настя летом отдыхает у дедушки в деревне Александровке. В воскресенье они собираются съездить на машине в село Фомино. Из Александровки в Фомино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Новомальцево до деревни Парахино, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Фомино. Есть и третий маршрут: в Новомальцева можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Фомино.
По шоссе Настя с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 50 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 3 км.
Решение.
Настя с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути соответствует длине гипотенузы прямоугольного треугольника с катетами 36 и 27. По теореме Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 50 км/ч дедушка с Настей потратят 45 : 50 = 0,9 часа или 54 минуты.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Настя с дедушкой проедут 12 километров со скоростью 60 км/ч. Следовательно, они затратят 12 : 60 = 0,2 часа или 12 минут. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 36 и 15. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Настя с дедушкой едут со скоростью 50 км/ч, следовательно, они затратят 39 : 50 = 0,78 часа или 46,8 минут.
Таким образом, Настя с дедушкой на весь путь затратят 46,8 + 12 = 58,8 минут.
3) По шоссе через Парахино. Расстояние, которое проедут Настя с дедушкой, проезжая через Парахино, равно сумме длин катетов прямоугольного треугольника с катетами 36 и 27. Таким образом, имеем, что искомое расстояние равно 36 + 27 = 63.
Двигаясь по шоссе со скоростью 60 км/ч Настя с дедушкой потратят 63 : 60 ≈ 1,05 часа или 63 минуты.
Таким образом, самый быстрый путь составит 54 минуты.
Ответ: 54.
* * * * *
Задача №18 про время движения Гены и дедушки по дороге
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гена с дедушкой, если поедут этим маршрутом.
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
Гена с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути соответствует длине гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 40 км/ч дедушка с Геной потратят 40 : 40 = 1 час или 60 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Гена с дедушкой проедут 22 километра со скоростью 60 км/ч. Следовательно, они затратят часа или 22 минуты. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 24 и 10. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч, следовательно, они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61 минута.
3) По шоссе через Кулаки. Расстояние, которое проедут Гена с дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Двигаясь по шоссе со скоростью 60 км/ч, Гена с дедушкой потратят часа или 56 минут.
Таким образом, самый быстрый путь составит 56 минут.
Ответ: 56.
* * * * *
Задача №19 для ОГЭ по математике про время и скорость движения Марины и дедушки по маршруту
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Марина с дедушкой, если поедут этим маршрутом.
Марина летом отдыхает у дедушки в деревне Ивановки. В пятницу они собираются съездить на машине в село Гавриловка. Из Ивановки в Гавриловку можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Пересыпкино до деревни Ольшанка, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Гавриловку. Есть и третий маршрут: в Пересыпкине можно свернуть на прямую грунтовую дорогу, которая идёт мимо пруда прямо в Гавриловку.
По шоссе Марина с дедушкой едут со скоростью 48 км/ч, а по грунтовой дороге — 25 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 1 км.
Решение.
Марина с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути соответствует длине гипотенузы прямоугольного треугольника с катетами 15 и 20. По теореме Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 25 км/ч, дедушка с Мариной потратят 25 : 25 = 1 час или 60 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Марина с дедушкой проедут 12 километров со скоростью 48 км/ч. Следовательно, они затратят 12 : 48 = 0,25 часа или 15 минут. Дальше по условию задачи они свернут на грунтовую дорогу, длина которой равна длине гипотенузы прямоугольного треугольника с катетами 8 и 15. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Марина с дедушкой едут со скоростью 25 км/ч, следовательно, они затратят 17 : 25 = 0,68 часа или 40,8 минут.
Таким образом, Марина с дедушкой на весь путь затратят 15 + 40,8 = 55,8 минут.
3) По шоссе через Ольшанку. Расстояние, которое проедут Марина с дедушкой, проезжая через Ольшанку, равно сумме длин катетов прямоугольного треугольника с катетами 15 и 20. Таким образом, искомое расстояние равно 15 + 20 = 35.
Двигаясь по шоссе со скоростью 48 км/ч, Марина с дедушкой потратят 35 : 48 60 = 43,75 минут.
Таким образом, самый быстрый путь составит 43,75 минут.
Ответ: 43,75.
Гриша летом отдыхает у дедушки в деревне ушаково в субботу они собираются съездить на машине
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Грушёвка, селе Абрамово, деревне Таловка и деревне Новая.
| Наименование продукта | д. Грушёвка | с. Абрамово | д. Таловка | д. Новая |
|---|---|---|---|---|
| Молоко (1 л) | 32 | 33 | 31 | 34 |
| Хлеб (1 батон) | 24 | 21 | 26 | 20 |
| Сыр «Российский» (1 кг) | 320 | 310 | 330 | 300 |
| Говядина (1 кг) | 390 | 360 | 370 | 420 |
| Картофель (1 кг) | 10 | 18 | 15 | 12 |
Гриша с дедушкой хотят купить 3 батона хлеба, 1,5 кг сыра «Российский» и 5 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Гриша летом отдыхает у дедушки в деревне Грушёвка. В понедельник они собираются съездить на велосипедах в село Абрамово на ярмарку.
Из деревни Грушёвка в село Абрамово можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Таловка до деревни Новая, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в село Абрамово. Есть и третий маршрут: в деревне Таловка можно свернуть на прямую тропинку в село Абрамово, которая идёт мимо пруда.
Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники.
По шоссе Гриша с дедушкой едут со скоростью 15 км/ч, а по лесной дорожке и тропинке — со скоростью 12 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 2 км.
Источник
12.05.2020 Математика 9 класс МА1990701-МА1990704 ответы и задания статград
ПОДЕЛИТЬСЯ
Тренировочная работа №5 статград по математике 9 класс пробное ОГЭ ответы и задания для вариантов: МА1990701, МА1990702, МА1990703, МА1990704. Официальная дата проведения работы: 12.05.2020 (12 мая 2020 год).
Ссылка для скачивания вариантов заданий (МА1990701-МА1990704): скачать
Ссылка для скачивания ответов и критериев для вариантов: скачать
Решать тренировочную работу №5 по математике 9 класс онлайн:
Некоторые задания и ответы с вариантов:
Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село Бережки. По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 50 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
1)Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр. Ответ: 2431
2)Найдите расстояние от деревни Ушаково до села Бережки по прямой. Ответ выразите в километрах. Ответ: 34
3)Сколько километров проедут Гриша с дедушкой, если они поедут по шоссе через Афонино? Ответ:46
4)Сколько времени затратят на дорогу Гриша с дедушкой, если они поедут сначала до деревни Дубёнки, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах. Ответ: 42
6)Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гриша с дедушкой, если поедут этим маршрутом. Ответ: 408
7)Родительский комитет закупил 20 пазлов для подарков детям в связи с окончанием учебного года, из них 11 с машинами и 9 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Илюша. Найдите вероятность того, что Илюше достанется пазл с машиной. Ответ: 0,55
8)Выписаны первые три члена арифметической прогрессии: 10; 6; 2; … Найдите 6-й член этой прогрессии.
12)Площадь параллелограмма ABCD равна 104. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
13)Какое из следующих утверждений верно? 1) Две различные прямые, перпендикулярные третьей прямой, параллельны. 2) Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то этот четырёхугольник является квадратом. 3) Все углы ромба равны. В ответе запишите номер выбранного утверждения.
14)Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 60 км. На следующий день он отправился обратно в город А, увеличив скорость на 10 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А.
15)Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 3,6, а AB=8.
17)В треугольнике ABC известны длины сторон AB= 84, AC = 98, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
18)Найдите расстояние от деревни Осинки до села Кудрино по прямой. Ответ выразите в километрах.
19)Сколько километров проедут Гена с дедушкой, если они поедут по шоссе через деревню Кулаки?
20)Сколько времени затратят на дорогу Гена с дедушкой, если они поедут сначала до Илькина, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.
21)Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гена с дедушкой, если поедут этим маршрутом.
22)Родительский комитет закупил 25 пазлов для подарков детям в связи с окончанием учебного года, из них 21 с машинами и 4 с видами городов. Подарки распределяются случайным образом между 25 детьми, среди которых есть Саша. Найдите вероятность того, что Саше достанется пазл с машиной.
26)Площадь параллелограмма ABCD равна 92.Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
27)Какое из следующих утверждений верно? 1) Площадь любого параллелограмма равна произведению длин его сторон. 2) Треугольник со сторонами 1, 2, 4 существует. 3) Основания любой трапеции параллельны. В ответе запишите номер выбранного утверждения.
28)Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 112 км. На следующий день он отправился обратно в город А, увеличив скорость на 9 км/ч. По пути он сделал остановку на 4 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.
30)Основания BC и AD трапеции ABCD равны соответственно 5 и 45, BD =15. Докажите, что треугольники CBD и BDA подобны.
Источник
Решение №2254 Володя летом отдыхает у дедушки в деревне Ёлочки. В воскресенье они собираются съездить на машине в село Кленовое.
Володя летом отдыхает у дедушки в деревне Ёлочки. В воскресенье они собираются съездить на машине в село Кленовое. Из деревни Ёлочки в село Кленовое можно проехать по прямой грунтовой дороге. Есть более длинный путь: по прямолинейному шоссе через деревню Сосенки до деревни Жуки, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в село Кленовое. Есть и третий маршрут: в деревне Сосенки можно свернуть на прямую грунтовую дорогу в село Кленовое, которая идёт мимо пруда.
Шоссе и грунтовые дороги образуют прямоугольные треугольники.
По шоссе Володя с дедушкой едут со скоростью 80 км/ч, а по грунтовой дороге – со скоростью 40 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 4 км.
Источник: ОГЭ Ященко 2022 (36 вар)
Задание 1
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
Решение
Ответ: 421
Задание 2
Сколько километров проедут Володя с дедушкой от деревни Ёлочки до села Кленового, если они поедут по шоссе через деревню Жуки?
Решение
По плану одна клетка равна 4 км, считаем клетки и умножаем на 4. Расстояние от Ёлочки до Кленового равно (посчитал всё на рисунке):
36 + 24 + 32 = 92 км
Ответ: 92
Задание 3
Найдите расстояние от деревни Сосенки до села Кленового по прямой. Ответ дайте в километрах.
Решение
Дорога по прямой (х) из Сосёнки в Кленовое является гипотенузой (рисунок из задания 2) прямоугольного треугольника, найдём её по теореме Пифагора:
х 2 = 24 2 + 32 2 = 576 + 1024 = 1600
х = √1600 = 40 км
Ответ: 40
Задание 4
Сколько минут затратят на дорогу из деревни Ёлочки в село Кленовое Володя с дедушкой, если поедут через деревню Жуки?
Решение
Расстояние между Ёлочки и Кленовым, через Жуки по трассе равно 92 км (2 задание). По трассе они едут со скоростью 80 км/ч, найдём время:
Переведём в минуты:
Ответ: 69
Задание 5
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Ёлочки, селе Кленовом, деревне Сосенки и деревне Жуки.
Володя с дедушкой хотят купить 5 л молока, 3 кг сыра «Российский» и 4 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Смотрим по таблице цену продуктов и находим стоимость покупки в каждом магазине.
Ёлочки :
5·42 + 3·320 + 4·26 =1274 рублей
Кленовое :
5·45 + 3·290 + 4·18 = 1167 рублей
Сосёнки :
5·38 + 3·270 + 4·24 = 1096 рублей
Жуки :
5·43 + 3·280 + 4·16 = 1119 рублей
Наименьшая стоимость 1096 рублей.
Источник
Пробный экзаменационный вариант «ОГЭ математика пробник 141 вариант» (2022)
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село Бережки.
По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге —50 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
2. Найдите расстояние от деревни Ушаково до села Бережки по прямой. Ответ выразите в километрах.
3. Сколько километров проедут Гриша с дедушкой, если они поедут по шоссе через Афонино?
4. Сколько времени затратят на дорогу Гриша с дедушкой, если они поедут сначала до деревни Дубёнки, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.
5. Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гриша с дедушкой, если поедут этим маршрутом.
Найдите значение выражения 3,8 + 2,9.
7. На координатной прямой отмечены числа 
Какое из следующих утверждений неверно?
1)
2)
3)
4)
8. Найдите значение выражения 
9. Найдите корень уравнения −5 + 9x = 10x + 4.
10. В таблице представлены результаты четырёх стрелков, показанные ими на тренировке.
Тренер решил послать на соревнования того стрелка, у которого относительная частота попаданий выше. Кого из стрелков выберет тренер? Укажите в ответе его номер.
11. Установите соответствие между графиками функций и формулами, которые их задают.
1)
2)
3)
В таблице под каждой буквой укажите соответствующий номер.
12. Период колебания математического маятника 


13. Решите неравенство
2)
4)
14. Бригада рабочих могла выполнить всю работу за 24 ч, если бы работали одновременно все рабочие. однако по плану в первый час работал один рабочий, во второй час — 2 рабочих, в третий — 3 и т. д. до тех пор, пока в работу не включились все рабочие. И только несколько часов перед завершением работала вся бригада. Время работы, предусмотренное планом, было бы сокращено на 6 часов, если бы с самого начала работы работала бы вся бригада, за исключением пяти рабочих. Найдите количество рабочих.
15.
Найдите больший угол равнобедренной трапеции 



16.
Касательные в точках A и B к окружности с центром O пересекаются под углом 12°. Найдите угол ABO. Ответ дайте в градусах.
17. 
18. 
19. Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120°, то смежный с ним равен 120°.
3) Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Решите уравнение
21. Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
22. Постройте график функции
и определите, при каких значениях 

23. В прямоугольном треугольнике 




24. В окружности через середину O хорды BD проведена хорда AC так, что дуги AB и CD равны. Докажите, что O — середина хорды AC.
25. Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село Бережки.
По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге —50 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Пользуясь описанием и рисунком можно заметить, что деревня Дубенки соответствует цифре 2, деревня Бережки — цифре 4, деревня Ушаково — цифре 3 и деревня Афонино —цифре 1.
2. Найдите расстояние от деревни Ушаково до села Бережки по прямой. Ответ выразите в километрах.
Расстояние от деревни Ушаково до села Бережки соответствует длине гипотенузы прямоугольного треугольника с катетами 30 и 16. По теореме Пифагора имеем:
3. Сколько километров проедут Гриша с дедушкой, если они поедут по шоссе через Афонино?
Расстояние, которое проедут Гриша с дедушкой, проезжая через Афонино, равно сумме длин катетов прямоугольного треугольника с катетами 30 и 16. Таким образом, имеем, что искомое расстояние равно 30 + 16 = 46.
4. Сколько времени затратят на дорогу Гриша с дедушкой, если они поедут сначала до деревни Дубёнки, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.
По шоссе Гриша с дедушкой проедут 18 километров со скоростью 60 км/ч. Следовательно, они затратят 18 : 60 = 0,3 часа или 18 минут. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 12 и 16. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Гриша с дедушкой едут со скоростью 50 км/ч, следовательно они затратят 20 : 50 = 0,4 часа или 24 минуты.
Таким образом, Гриша с дедушкой на весь путь затратят 24 + 18 = 42 минуты.
5. Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гриша с дедушкой, если поедут этим маршрутом.
Гриша с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути равна длине гипотенузы прямоугольного треугольника с катетами 30 и 16. По теореме Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 50 км/ч дедушка с Гришой потратят 34 : 50 = 0,68 часа или 40,8 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Гриша с дедушкой проедут 18 километров со скоростью 60 км/ч. Следовательно, они затратят 18 : 60 = 0,3 часа или 18 минут. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 12 и 16. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Гриша с дедушкой едут со скоростью 50 км/ч, следовательно они затратят 20 : 50 = 0,4 часа или 24 минуты.
Таким образом, Гриша с дедушкой на весь путь затратят 24 + 18 = 42 минуты.
3) По шоссе через Афонино. Расстояние, которое проедут Гриша с дедушкой, проезжая через Афонино, равно сумме длин катетов прямоугольного треугольника с катетами 30 и 16. Таким образом, имеем, что искомое расстояние равно 30 + 16 = 46.
Двигаясь по шоссе со скоростью 60 км/ч Гриша с дедушкой потратят 46 : 60 часа или 46 минут.
Таким образом, самый быстрый путь составит 40,8 минут.
Найдите значение выражения 3,8 + 2,9.
Найдем значение выражения: 3,8 + 2,9 = 6,7.
7. На координатной прямой отмечены числа 
Какое из следующих утверждений неверно?
1)
2)
3)
4)
Заметим, что 



1) 

2) 


3) 

4) 

Ответ указан под номером 2.
8. Найдите значение выражения 
Подставим значение
9. Найдите корень уравнения −5 + 9x = 10x + 4.
10. В таблице представлены результаты четырёх стрелков, показанные ими на тренировке.
Источник