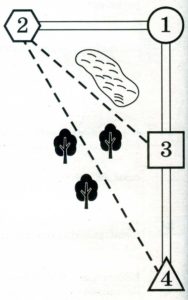
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
| Населенные пункты | д. Березовка | с. Игнатьево | д. Николаевка | д. Свистуха |
| Цифры | 1 | 2 | 4 | 3 |
Ответ: 1243.
Немного дополню картинку.
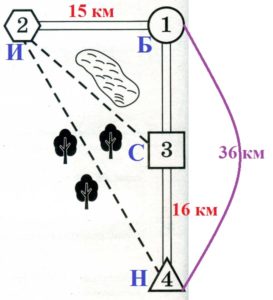
2. Сколько километров проедут Миша с дедушкой, если они поедут по шоссе через Берёзовку?
Миша с дедушкой выезжают из Николаевки. Если ехать по шоссе, то им надо проехать до Березовки 36 км, а затем до Игннатьево еще 15 км. Итого 36 + 15 = 51 км.
Ответ: 51.
3. Найдите расстояние от д. Николаевка до с. Игнатьево по прямой. Ответ дайте в километрах.
Дорога по лесной дорожке ни что иное, как гипотенуза C прямоугольного треугольника с катетами 36 км и 15 км.
Найдем ее по теореме Пифагора.
С2 = 362 + 152 = 1 296 + 225 = 1 521;
С = √1521 = 39.
Ответ: 39.
4. Сколько минут затратят на дорогу Миша с дедушкой, если поедут на станцию через Берёзовку?
Чтобы найти время надо расстояние поделить на скорость.
Расстояние равно 51 км (задача 2), скорость по шоссе равна 20 км/ч (из условия задачи).
Находим время:
51 : 20 = 2,55 ч = 2,55 · 60 = 153 минуты.
Ответ: 153.
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответ укажите сколько минут потратят на дорогу Миша с дедушкой, если проедут этим маршрутом.
Время пути Миши и дедушки по шоссе мы нашли — 153 минуты.
Найдем время пути по лесной дороге.
Длина дороги равна 39 км (задача 3), а скорость путешественников равна 15 км/ч (условие задачи).
Находим время по лесной дорожке.
39 : 15 = 2,6 ч = 2,6 · 60 = 156 минут.
Но еще есть и третий маршрут — это путь от Николаевки до Свистухи по шоссе, а затем от Свистухи до Игнатьево по лесной дороге.
Найдем время пути от Николаевки до Свистухи: 16 : 20 = 0,8 ч = 0,8 · 60 = 48 минут.
И найдем время пути от Свистухи до Игнатьево.
Здесь не все так просто, т.к. длина лесной дороги нам не известна. Найдем ее по теореме Пифагора.
с2 = 152 + (36 — 16)2 = 225 + 400 = 625;
с = √625 = 25.
Время по лесной дороге: 25 : 15 = 5/3 ч = 5/3 · 60 = 100 минут.
Подведем итог. Время, которое затратят Миша с дедушкой, поехав через Свистуху и лесную дорогу, равно 48 + 100 = 148 минутам. Этот путь менее затратный по времени.
Ответ: 148.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
1.
Математика
Модель ОГЭ — 2020
Практические
задачи
Титова Л.А.
2. Основные изменения в структуре ОГЭ-2020
изменения в ОГЭ плавные и поэтапные
ОГЭ будет проходить по новому ФГОС
исчезновение модулей «алгебра» и «геометрия»
появление «практических задач»
www.fipi.ru
3. Практические задачи
реальные жизненные ситуации
одна ситуация объединяет в себе несколько задач
адресованы тем, кто не пойдёт в старшую школу
содержат акценты на сложности, встречающиеся в
10-11 классах
www.fipi.ru
4. Практические задачи
распознавание объектов
простейшие задачи вычислительного характера
вычисление площади фигуры (или сравнение площадей
фигур)
вычисление длины отрезка
задача на оптимальный выбор
5. Задача 1
5
01.10.2019
Задача 1
При входе на участок напротив ворот
находится гараж, а за гаражом –
жилой дом. Площадь, занятая
гаражом, равна 48 кв. м. Слева от
ворот находится большой газон,
отмеченный на плане цифрой 5. На
газоне имеются круглый бассейн,
беседка и две ромбовидные клумбы.
Беседка отмечена на плане цифрой 4.
При въезде на участок имеется
площадка, вымощенная тротуарной
плиткой размером 0,2 м х 0,1 м и
обозначенная на плане цифрой 7.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены
на плане. Заполните таблицу, в бланк перенесите последовательность четырёх цифр.
Объекты
Цифры
жилой
дом
1
гараж
2
бассейн
3
клумбы
6
6. Задача 1
6
03.01.2020
Задача 1
2. Найдите площадь, которую занимает одна клумба. Ответ дайте в квадратных
метрах.
Объекты
Цифры
жилой
дом
1
гараж
2
бассейн
3
клумбы
6
Ответ: 4
7. Задача 1
7
03.01.2020
Задача 1
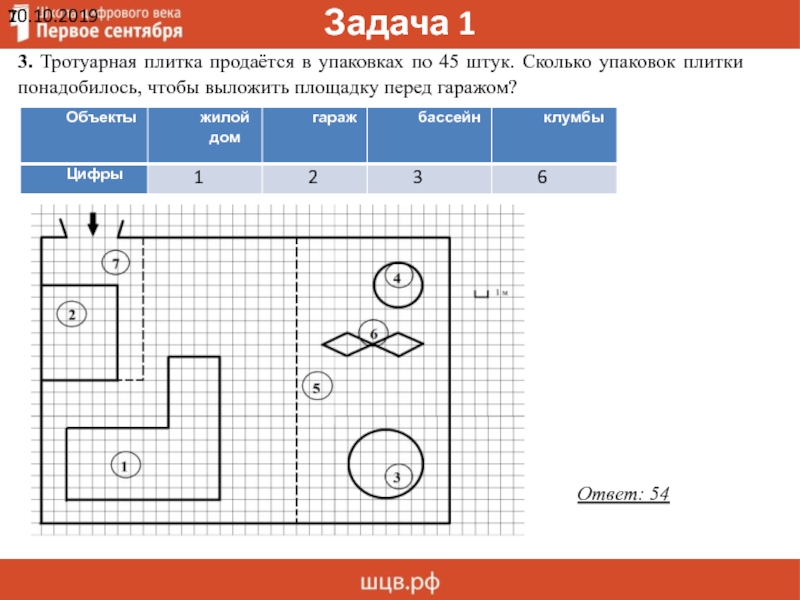
3. Тротуарная плитка продаётся в упаковках по 45 штук. Сколько упаковок плитки
понадобилось, чтобы выложить площадку перед гаражом?
Объекты
Цифры
жилой
дом
1
гараж
2
бассейн
3
клумбы
6
Ответ: 54
8. Задача 1
8
03.01.2020
Задача 1
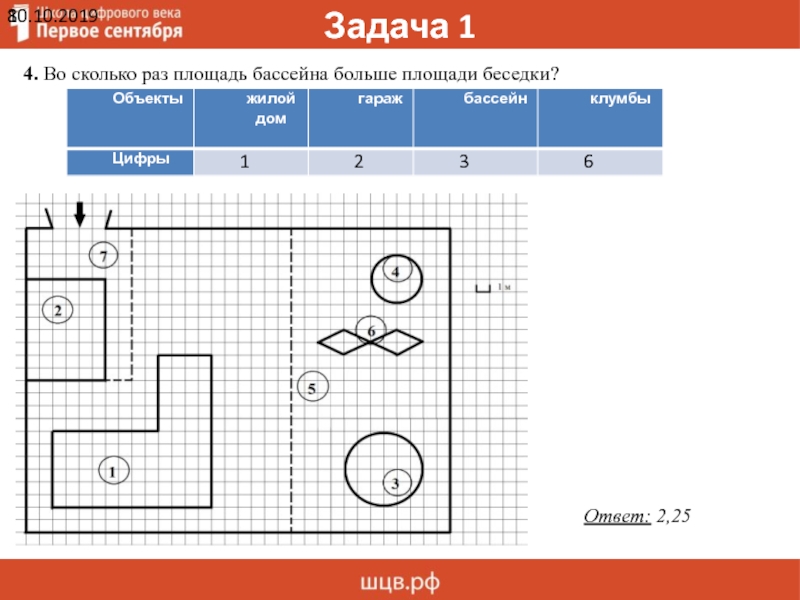
4. Во сколько раз площадь бассейна больше площади беседки?
Объекты
Цифры
жилой
дом
1
гараж
2
бассейн
3
клумбы
6
Ответ: 2,25
9. Задача 1
9
03.01.2020
Задача 1
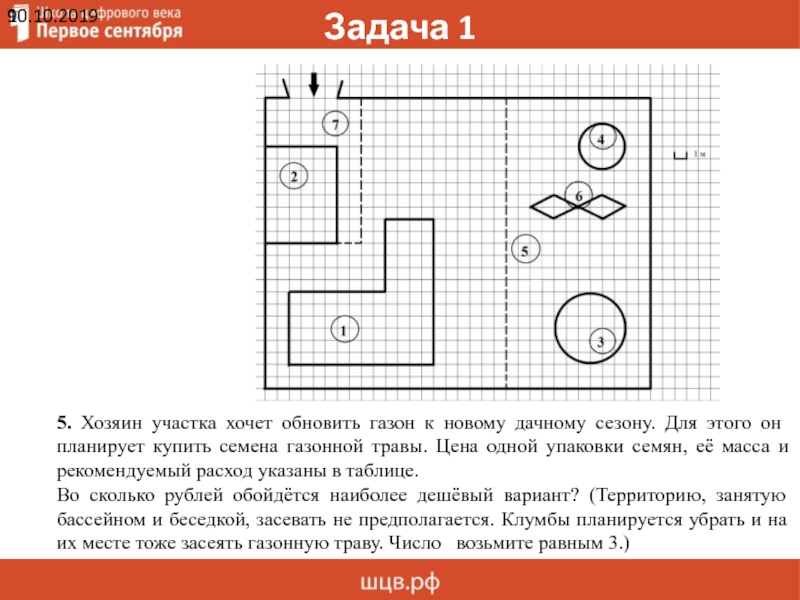
5. Хозяин участка хочет обновить газон к новому дачному сезону. Для этого он
планирует купить семена газонной травы. Цена одной упаковки семян, её масса и
рекомендуемый расход указаны в таблице.
Во сколько рублей обойдётся наиболее дешёвый вариант? (Территорию, занятую
бассейном и беседкой, засевать не предполагается. Клумбы планируется убрать и на
их месте тоже засеять газонную траву. Число возьмите равным 3.)
10. Задача 1
10
03.01.2020
Задача 1
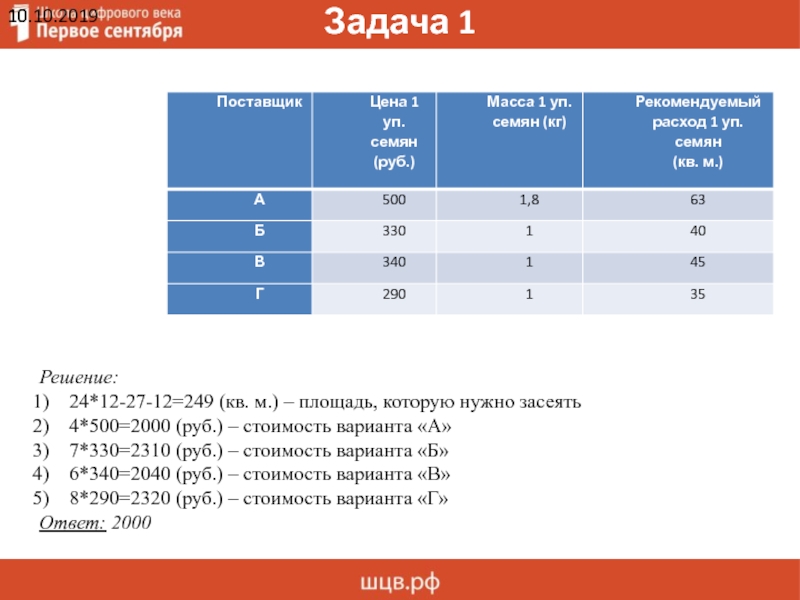
Поставщик
Цена 1 уп.
семян
(руб.)
Масса 1 уп.
семян (кг)
Рекомендуемый
расход 1 уп. семян
(кв. м.)
А
500
1,8
63
Б
330
1
40
В
340
1
45
Г
290
1
35
Решение:
1) 24*12-27-12=249 (кв. м.) – площадь, которую нужно засеять
2) 4*500=2000 (руб.) – стоимость варианта «А»
3) 7*330=2310 (руб.) – стоимость варианта «Б»
4) 6*340=2040 (руб.) – стоимость варианта «В»
5) 8*290=2320 (руб.) – стоимость варианта «Г»
Ответ: 2000
11. Задача 2
11
03.01.2020
Задача 2
На
рисунке
изображен
план
однокомнатной квартиры в 16-этажном
жилом доме (сторона каждой клетки на
плане равна 0,5 м). Окна квартиры
выходят на север. При входе в квартиру
располагается прихожая. Справа от
прихожей находится санузел, а слева –
вход в комнату. Санузел имеет общую
стену с кухней, отмеченную на плане
цифрой 2. Комната имеет наибольшую
площадь из всех помещений. Из кухни
есть выход на балкон. Пол санузла
выложен плиткой размером 25смх25см.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены
на плане. Заполните таблицу, в бланк перенесите последовательность четырёх цифр.
Объекты
Цифры
санузел
прихожая
балкон
комната
5
4
3
1
12. Задача 2
12
03.01.2020
Задача 2
2. Плитка для пола продается в упаковках по 8 штук. Сколько упаковок плитки
понадобилось, чтобы выложить пол санузла?
Объекты
Цифры
санузел
прихожая
балкон
комната
5
4
3
1
Ответ: 8
13. Задача 2
13
03.01.2020
Задача 2
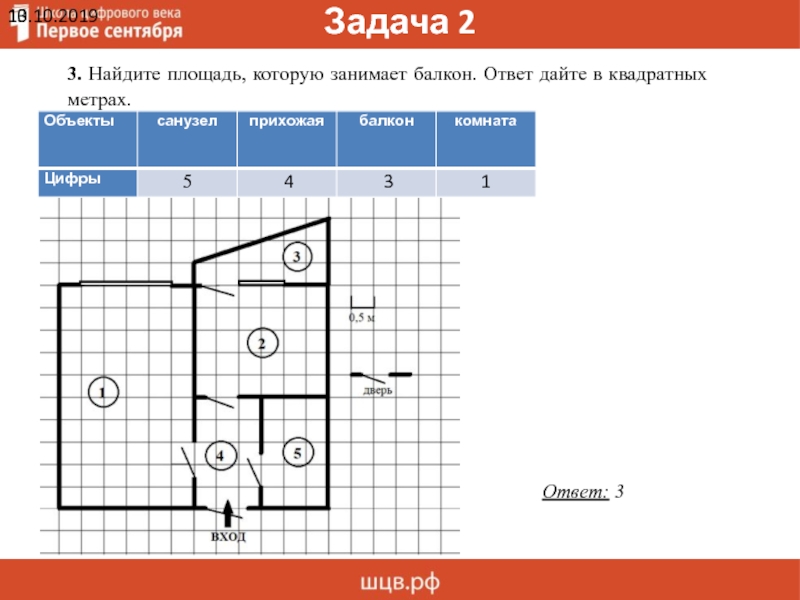
3. Найдите площадь, которую занимает балкон. Ответ дайте в квадратных
метрах.
Объекты
Цифры
санузел
прихожая
балкон
комната
5
4
3
1
Ответ: 3
14. Задача 2
14
03.01.2020
Задача 2
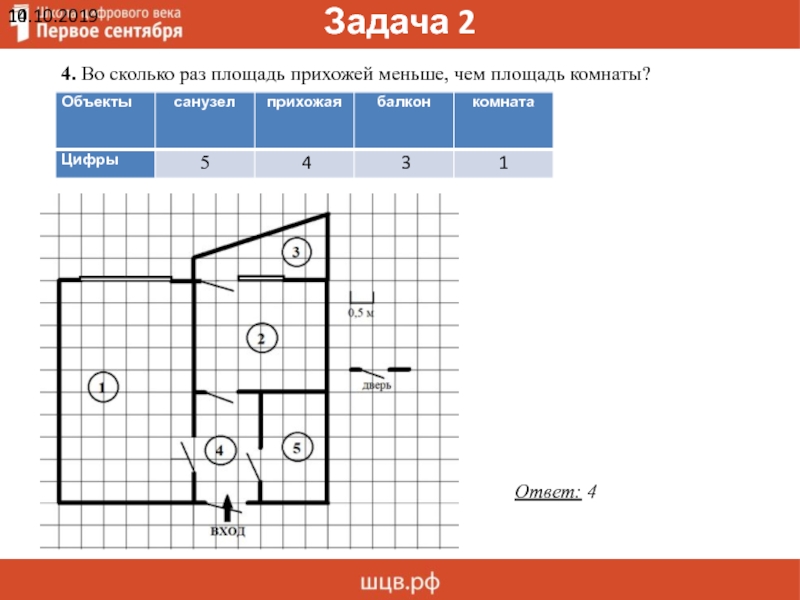
4. Во сколько раз площадь прихожей меньше, чем площадь комнаты?
Объекты
Цифры
санузел
прихожая
балкон
комната
5
4
3
1
Ответ: 4
15. Задача 2
5. В квартире планируется установить стиральную машину.
Характеристики стиральных машин, условия подключения и доставки
приведены в таблице. Планируется купить стиральную машину с
фронтальной загрузкой по глубине не превосходящей 42 см.
Мод
ель
Вместимость
барабана
(кг)
Загрузка
белья
Цена
машины
(руб)
Подключе
ние
(руб)
Условия
доставки
Габариты
(высоташиринаглубина)
А
7
28 000
1700
бесплатно
85х60х45
Б
5
вертикальна
я
фронтальная
24 000
4500
85х60х40
В
5
фронтальная
25 000
5000
Г
6,5
фронтальная
24 000
4500
Д
6
фронтальная
28 000
1700
10% от
стоимости
машины (без
учёта
подключения)
10% от
стоимости
машины (без
учёта
подключения)
10% от
стоимости
машины (без
учёта
подключения)
бесплатно
85х60х40
85х60х44
85х60х45
16. Задача 2
Модель
Вместимость
барабан
а (кг)
Загрузка
белья
Цена
машины
(руб)
Подключение
(руб)
Условия
доставки
Габариты
(высоташиринаглубина)
Е
6
вертикальная
27 600
2300
бесплатно
89х60х40
Ж
6
вертикальная
27 585
1900
10% от
стоимости
машины (без
учёта
подключения)
89х60х40
З
6
фронтальная
20 000
6300
15% от
стоимости
машины (без
учёта
подключения)
85х60х42
И
5
фронтальная
27 000
1800
бесплатно
85х60х40
К
5
вертикальная
27 000
1800
10% от
стоимости
машины (без
учёта
подключения)
85х60х40
Сколько рублей будет стоить наиболее дешевый подходящий
вариант вместе с подключением и доставкой?
Ответ: 2880 (вариант «И»)
17. Задача 3
На рисунке изображён план однокомнатной
квартиры в 16-этажном жилом доме
(сторона каждой клетки на плане равна 0,4
м). Окна квартиры выходят на север. При
входе в квартиру располагается прихожая.
Справа от прихожей находится санузел, а
слева – вход в комнату. Санузел имеет
общую стену с кухней, отмеченную на
плане
цифрой
5.
Комната
имеет
наибольшую площадь из всех помещений,
из неё есть выход на просторную лоджию.
Пол лоджии выложен плиткой размером
20смх20см.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены
на плане. Заполните таблицу, в бланк перенесите последовательность четырёх цифр.
Объекты
Цифры
комната
лоджия
прихожая
санузел
1
2
4
3
18. Задача 3
18
03.01.2020
Задача 3
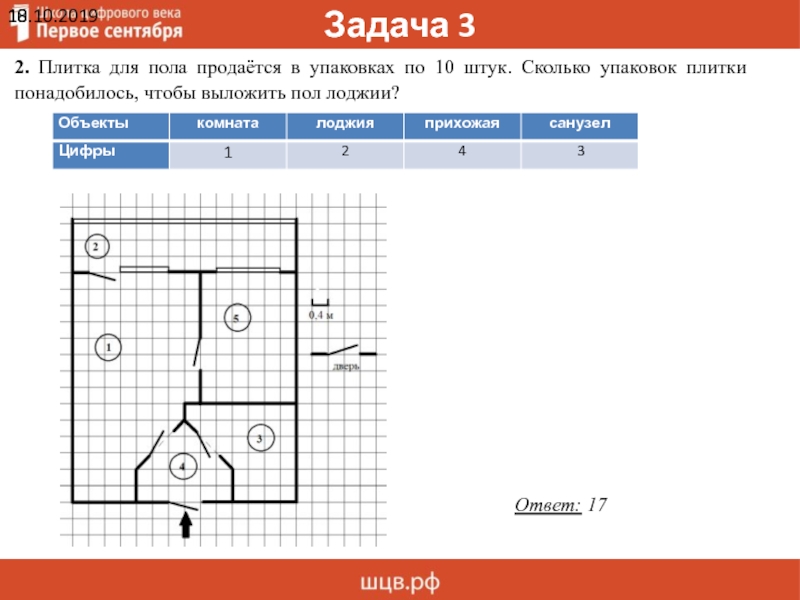
2. Плитка для пола продаётся в упаковках по 10 штук. Сколько упаковок плитки
понадобилось, чтобы выложить пол лоджии?
Объекты
Цифры
комната
лоджия
прихожая
санузел
1
2
4
3
Ответ: 17
19. Задача 3
19
03.01.2020
Задача 3
3. Найдите площадь, которую занимает санузел. Ответ дайте в квадратных метрах.
Объекты
Цифры
комната
лоджия
прихожая
санузел
1
2
4
3
Ответ: 5,04
20. Задача 3
20
03.01.2020
Задача 3
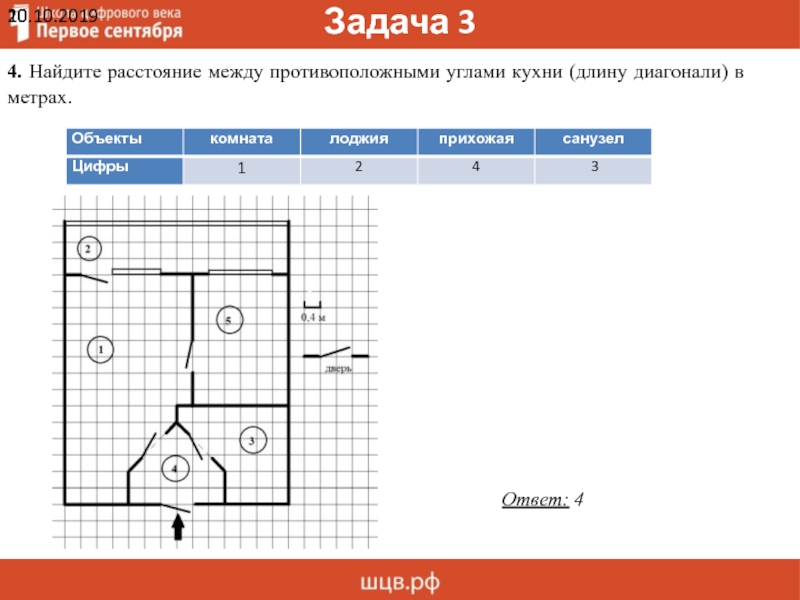
4. Найдите расстояние между противоположными углами кухни (длину диагонали) в
метрах.
Объекты
Цифры
комната
лоджия
прихожая
санузел
1
2
4
3
Ответ: 4
21. Задача 3
21
03.01.2020
Задача 3
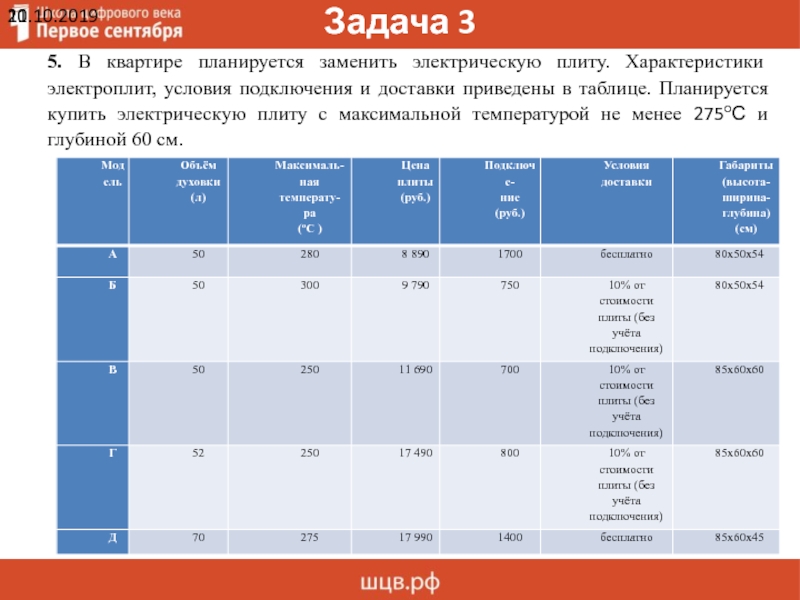
5. В квартире планируется заменить электрическую плиту. Характеристики
электроплит, условия подключения и доставки приведены в таблице. Планируется
купить электрическую плиту с максимальной температурой не менее 275оС и
глубиной 60 см.
Мод
ель
Объём
духовки
(л)
Максимальная
температура
о
( С)
Цена
плиты
(руб.)
Подключ
ение
(руб.)
Условия
доставки
Габариты
(высоташиринаглубина)
(см)
А
50
280
8 890
1700
бесплатно
80х50х54
Б
50
300
9 790
750
10% от
стоимости
плиты (без
учёта
подключения)
80х50х54
В
50
250
11 690
700
10% от
стоимости
плиты (без
учёта
подключения)
85х60х60
Г
52
250
17 490
800
10% от
стоимости
плиты (без
учёта
подключения)
85х60х60
Д
70
275
17 990
1400
бесплатно
85х60х45
22. Задача 3
22
03.01.2020
Задача 3
Модель
Объём
духовки (л)
Максимальная
температура
(оС )
Цена
плиты
(руб.)
Подключение
(руб.)
Условия
доставки
Габарит
ы
(высоташиринаглубина)
(см)
Е
58
250
18 890
1500
бесплатно
85х50х60
Ж
54
270
18 900
750
15% от
стоимости
плиты (без
учёта
подключения)
85х50х60
З
46
250
20 990
750
10% от
стоимости
плиты (без
учёта
подключения)
87х50х60
И
70
275
21 690
1500
бесплатно
85х50х60
К
67
250
22 990
1500
бесплатно
85х50х60
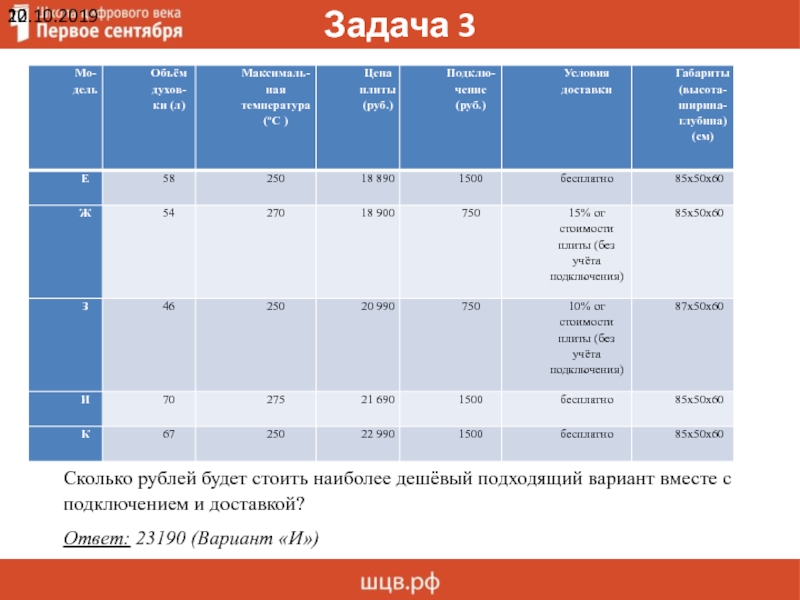
Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с
подключением и доставкой?
Ответ: 23190 (Вариант «И»)
23. Задача 4
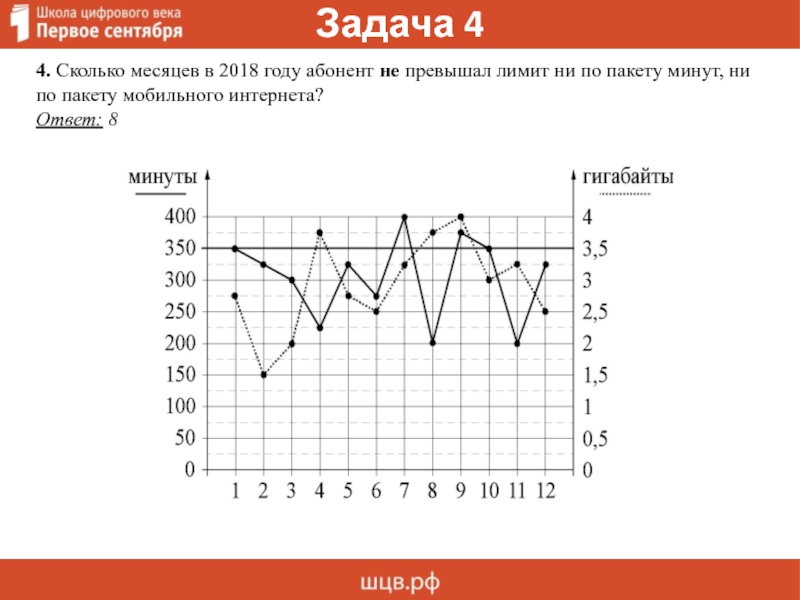
На графике точками изображено количество минут, потраченных на исходящие
вызовы, и количество гигабайтов мобильного интернета, израсходованных
абонентом в процессе пользования смартфоном, за каждый месяц 2018 года. Для
удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и
пунктирными линиями соответственно.
24. Задача 4
1. Определите, какие месяцы соответствуют указанному в таблице количеству
израсходованных гигабайтов. Заполните таблицу, в ответ запишите подряд
числа, соответствующие номерам месяцев, без пробелов, запятых и других
дополнительных символов (например, для месяцев май, январь, ноябрь, август
в ответ нужно записать число 51118).
Израсходованные
гигабайты
4 ГБ
1,5 ГБ
2 ГБ
3 ГБ
Номер месяца
9
2
3
10
2. Сколько рублей
потратил абонент на
услуги связи в
сентябре?
Ответ: 475
25. Задача 4
В течение года абонент пользовался тарифом «Стандартный», абонентская плата по
которому составляет 300 рублей в месяц. При условии нахождения абонента на
территории РФ в абонентскую плату тарифа «Стандартный» входит:
• пакет минут, включающий 350 минут исходящих вызовов на номера,
зарегистрированные на территории РФ;
• пакет интернета, включающий 3,5 гигабайта мобильного интернета;
• пакет SMS, включающий 150 SMS в месяц;
• безлимитные бесплатные входящие вызовы.
Стоимость минут, интернета и SMS сверх пакета указана в таблице.
Исходящие вызовы
Мобильный интернет:
дополнительные пакеты по 0,5 Гб
3 руб./мин.
100 руб. за пакет
SMS
2 руб./шт.
Абонент не пользовался услугами связи в роуминге и не звонил на номера,
зарегистрированные за рубежом. За весь год абонент отправил 120 SMS.
3. Сколько месяцев в 2018 году абонент не превышал лимит по пакету
исходящих минут?
Ответ: 10
26. Задача 4
4. Сколько месяцев в 2018 году абонент не превышал лимит ни по пакету минут, ни
по пакету мобильного интернета?
Ответ: 8
27. Задача 4
5. В конце 2018 года оператор связи предложил абоненту перейти на новый тариф.
Его условия приведены в таблице.
Стоимость перехода на тариф
0 руб.
Абонентская плата в месяц
350 руб.
в абонентскую плату ежемесячно включены:
пакет исходящих минут
300 минут
пакет мобильного интернета
4 ГБ
пакет SMS
150 SMS
после расходования пакетов:
входящие вызовы
0 руб./мин.
исходящие вызовы*
1,5 руб./мин.
мобильный
интернет: 80 руб. за пакет
дополнительные пакеты по 0,5 Гб
SMS
3 руб./шт.
*исходящие вызовы на номера,
зарегистрированные
на
территории РФ
Абонент решает, перейти ли ему
на новый тариф, посчитав,
сколько бы он потратил на
услуги связи за 2018 г., если бы
пользовался им. Если получится
меньше, чем он потратил
фактически за 2018 г., то абонент
примет решение сменить тариф.
Перейдёт ли абонент на новый тариф?
В ответе запишите ежемесячную абонентскую плату по тарифу, который выберет
абонент на 2019 год.
Ответ: 300
28. Задача 5
28
03.01.2020
Задача 5
Иван Викторович решил построить на дачном участке теплицу длиной NP=4 м. Для
этого он сделал прямоугольный фундамент. Для каркаса теплицы Иван Викторович
заказывает металлические дуги в форме полуокружностей длиной 4,8 м каждая и
плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке
прямоугольником ACDB. Точки A и B – соответственно середины отрезков MO и ON.
1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между
соседними дугами было не более 60 см?
Ответ: 8
29. Задача 5
29
03.01.2020
Задача 5
Иван Викторович решил построить на дачном участке теплицу длиной NP=4 м. Для
этого он сделал прямоугольный фундамент. Для каркаса теплицы Иван Викторович
заказывает металлические дуги в форме полуокружностей длиной 4,8 м каждая и
плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке
прямоугольником ACDB. Точки A и B – соответственно середины отрезков MO и ON.
2. Найдите примерную ширину MN теплицы в сантиметрах. Число
возьмите равным 3.
Ответ: 320
30. Задача 5
30
03.01.2020
Задача 5
Иван Викторович решил построить на дачном участке теплицу длиной NP=4 м. Для этого
он сделал прямоугольный фундамент. Для каркаса теплицы Иван Викторович заказывает
металлические дуги в форме полуокружностей длиной 4,8 м каждая и плёнку для обтяжки.
В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB.
Точки A и B – соответственно середины отрезков MO и ON.
3. Найдите примерную площадь участка внутри теплицы в квадратных
метрах. Число возьмите равным 3.
Ответ: 12,8
31. Задача 5
31
03.01.2020
Задача 5
Иван Викторович решил построить на дачном участке теплицу длиной NP=4 м. Для
этого он сделал прямоугольный фундамент. Для каркаса теплицы Иван Викторович
заказывает металлические дуги в форме полуокружностей длиной 4,8 м каждая и
плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке
прямоугольником ACDB. Точки A и B – соответственно середины отрезков MO и ON.
4. Сколько квадратных метров плёнки нужно купить для передней и задней
стенок, если с учётом крепежа её нужно покупать с запасом 10%? Число
возьмите равным 3. Результат округлите до десятых.
Ответ: 8,4
32. Задача 5
32
03.01.2020
Задача 5
Иван Викторович решил построить на дачном участке теплицу длиной NP=4 м. Для
этого он сделал прямоугольный фундамент. Для каркаса теплицы Иван Викторович
заказывает металлические дуги в форме полуокружностей длиной 4,8 м каждая и плёнку
для обтяжки. В передней стенке планируется вход, показанный на рисунке
прямоугольником ACDB. Точки A и B – соответственно середины отрезков MO и ON.
5. Найдите примерную высоту входа в теплицу в сантиметрах. Число
возьмите равным 3. Результат округлите до целых.
Ответ: 139
33. Задача 6
Миша летом отдыхает у дедушки в деревне Кузьминки. В
субботу они собираются съездить на велосипедах в село
Борисово в магазин. Из Кузьминок в Борисово можно
проехать по прямой лесной дорожке. Есть более длинный
путь по шоссе – через деревню Соловьи до деревни
Подлипки, где нужно повернуть под прямым углом налево на
другое шоссе, ведущее в Борисово. Есть и третий маршрут: в
Соловьях можно свернуть на прямую тропинку, которая идёт
мимо пруда прямо в Борисово.
1. Пользуясь описанием, определите, какими цифрами на
плане обозначены населённые пункты. В ответ запишите
полученную последовательность четырёх цифр.
Населённые
пункты
Цифры
д. Подлипки
1
с. Борисово
2
д. Кузьминки
4
д. Соловьи
3
34. Задача 6
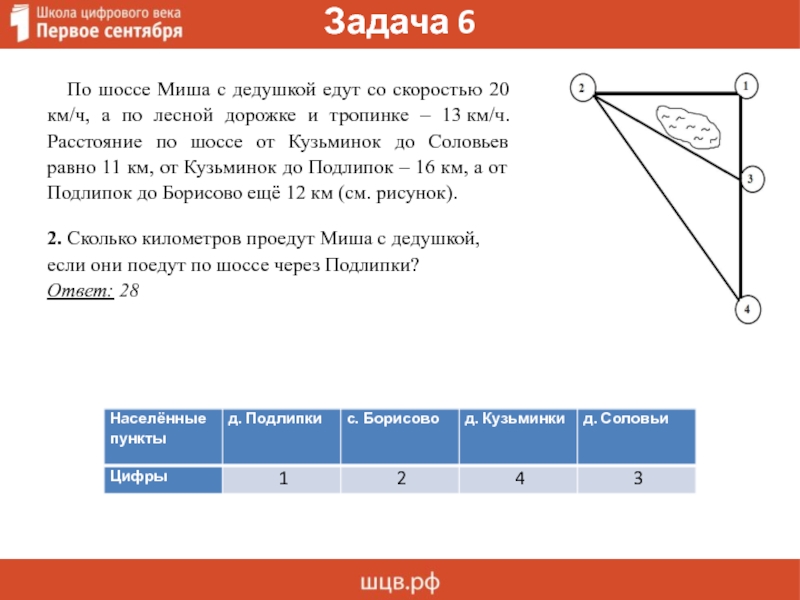
По шоссе Миша с дедушкой едут со скоростью 20
км/ч, а по лесной дорожке и тропинке – 13 км/ч.
Расстояние по шоссе от Кузьминок до Соловьев
равно 11 км, от Кузьминок до Подлипок – 16 км, а от
Подлипок до Борисово ещё 12 км (см. рисунок).
2. Сколько километров проедут Миша с дедушкой,
если они поедут по шоссе через Подлипки?
Ответ: 28
Населённые
пункты
Цифры
д. Подлипки
1
с. Борисово
2
д. Кузьминки
4
д. Соловьи
3
35. Задача 6
По шоссе Миша с дедушкой едут со скоростью 20
км/ч, а по лесной дорожке и тропинке – 13 км/ч.
Расстояние по шоссе от Кузьминок до Соловьев равно
11 км, от Кузьминок до Подлипок – 16 км, а от
Подлипок до Борисово ещё 12 км (см. рисунок).
3. Найдите расстояние от д. Кузьминки до с. Борисово
по прямой. Ответ выразите в километрах.
Ответ: 20
Населённые
пункты
Цифры
д. Подлипки
1
с. Борисово
2
д. Кузьминки
4
д. Соловьи
3
36. Задача 6
По шоссе Миша с дедушкой едут со скоростью 20 км/ч, а
по лесной дорожке и тропинке – 13 км/ч. Расстояние по
шоссе от Кузьминок до Соловьев равно 11 км, от
Кузьминок до Подлипок – 16 км, а от Подлипок до
Борисово ещё 12 км (см. рисунок).
4. Сколько времени затратят на дорогу Миша с дедушкой,
если поедут через Подлипки? Ответ выразите в минутах.
Ответ: 84
Населённые
пункты
Цифры
д. Подлипки
1
с. Борисово
2
д. Кузьминки
4
д. Соловьи
3
37. Задача 6
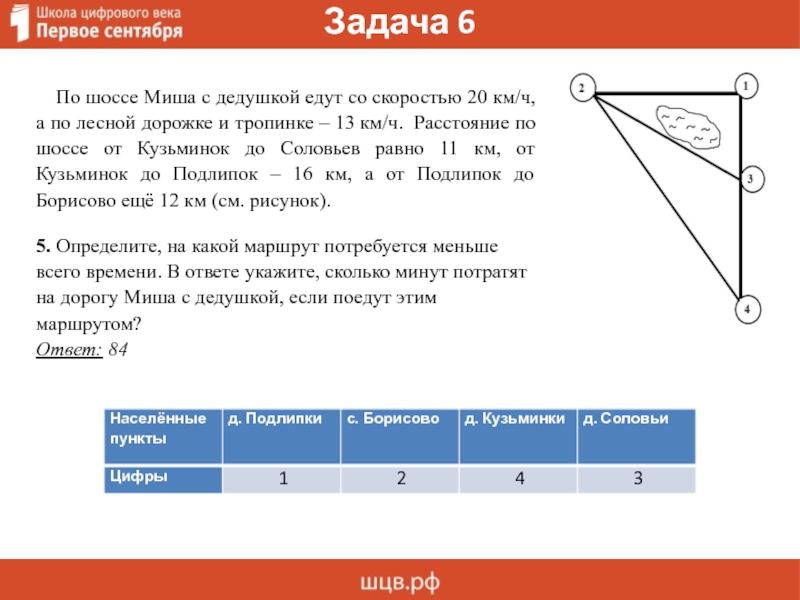
По шоссе Миша с дедушкой едут со скоростью 20 км/ч,
а по лесной дорожке и тропинке – 13 км/ч. Расстояние по
шоссе от Кузьминок до Соловьев равно 11 км, от
Кузьминок до Подлипок – 16 км, а от Подлипок до
Борисово ещё 12 км (см. рисунок).
5. Определите, на какой маршрут потребуется меньше
всего времени. В ответе укажите, сколько минут потратят
на дорогу Миша с дедушкой, если поедут этим
маршрутом?
Ответ: 84
Населённые
пункты
Цифры
д. Подлипки
1
с. Борисово
2
д. Кузьминки
4
д. Соловьи
3
38. Итог
38
03.01.2020
Итог
• Основная задача – развитие умения получать пользу от
математики в повседневных ситуациях.
• Появление геометрических сюжетов, где необходимы
вычислительные навыки. Особенно важно – площади и
длины.
• Естественные задачи на проценты (вычисление платежей,
скидок, наценок и т.п.)
• Появление оптимизационных задач (время, платежи,
распределение ресурсов)
• Появление простейших задач на представление и анализ
данных (диаграммы, таблицы)
39. Контакты издательства «Интеллект-центр»
Адрес: 125445, г. Москва,
Ул. Смольная, д. 24А, офис 712
Телефон: +7 (495) 660-34-53
Email: [email protected]
Сайт: https://www.intellectcentre.ru/
Ответ:
1. 51 км проедет Миша с дедушкой,если они поедут по шоссе через Берёзовку.
2. 153 минуты затратят на дорогу Миша с дедушкой, если поедут на станцию через Берёзовку
Пошаговое объяснение:
Номера деревень и расстояние между ними:
д.Игнатьево №2 Расстояние от д.Игнатьево до д.Березовка — 15 км
д.Березовка №1 Расстояние от д.Березовка до д.Свистуха 36 — 16 = 20 км
д.Свистуха №3 Расстояние от д.Свистуха до д.Николаевка 16 км
д.Николаевка №4 Расстояние от д.Николаевка до д.Березовка — 36 км
1. 36 км + 15 км = 51 км проедет Миша с дедушкой,если они поедут по шоссе через Берёзовку. (51 км = 36 км от д.Николаевка до д. Березовка + 15 км от д.Березовка до д.Игнатьево)
2. Расстояние от д.Николаевка до д.Игнатьево — 51 км, скорость по шоссе 20 км/час
51 км : 20 км/час = 2,55 час * 60 мин = 153 минуты затратят на дорогу Миша с дедушкой, если поедут на станцию через Берёзовку
Миша летом отдыхает у дедушки и бабушки в деревне Николаевке. Миша с дедушкой собираются съездить на велосипедах в село Игнатьево на железнодорожную станцию. Из Николаевки в Игнатьево можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Свистуху до деревни Берёзовки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Игнатьево. Есть и третий маршрут: в Свистухе можно свернуть на прямую тропинку, которая идёт мимо пруда прямо в Игнатьево.
По шоссе Миша с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Николаевки до Свистухи равно 16 км, от Николаевки до Берёзовки – 36 км, а от Берёзовки до Игнатьево 15 км.
Задание 1
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Решение
Из Николаевки (4) в Игнатьево можно проехать по прямой лесной дорожке.
Есть более длинный путь по шоссе – через деревню Свистуху (3) до деревни Берёзовки (1), где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Игнатьево (2).
Есть и третий маршрут: в Свистухе можно свернуть на прямую тропинку, которая идёт мимо пруда прямо в Игнатьево.
Ответ: 1243.
Задание 2
Сколько километров проедут Миша с дедушкой, если они поедут по шоссе через Берёзовку?
Решение
Миша с дедушкой собираются съездить из д. Николаевка в с. Игнатьево.
До д. Берёзовка они будут ехать 36 км, далее из Берёзовки в с. Игнатьево ещё 15 км, всего:
36 + 15 = 51 км
Ответ: 51.
Задание 3
Найдите расстояние от д. Николаевка до с. Игнатьево по прямой. Ответ дайте в километрах.
Решение
Получаем прямоугольный треугольник НИБ в котором нужно найти гипотенузу НИ. По теореме Пифагора:
НИ2 = НБ2 + БИ2
НИ2 = 362 + 152
НИ2 = 1296 + 225
НИ2 = 1521
НИ = √1521 = 39 км
Ответ: 39.
Задание 4
Сколько минут затратят на дорогу Миша с дедушкой, если поедут на станцию через Берёзовку?
Решение
Через станцию Берёзовку расстояние 51 км, и дорога идёт по шоссе, значит они едут со скоростью 20 км/ч, тогда время равно:
t=frac{S}{v}=frac{51}{20}=2frac{11}{20}=2,55
Это время в часах, переведём в минуты:
2,55·60 = 153 минуты
Ответ: 153.
Задание 5
Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Миша с дедушкой, если поедут этим маршрутом.
Решение:
1-я дорога через Берёзовку – 153 минуты (из задания 4).
2-я дорога до Игнатьево по прямой 39 км (из задания 3), она лестная, значит скорость 15 км/ч, тогда время:
t=frac{S}{v}=frac{39}{15}=2frac{9}{15}=2frac{3}{5}=2,6
Переведём в минуты:
2,6·60 = 156 минут
3-я дорога: в Свистухе можно свернуть на прямую тропинку, которая идёт мимо пруда прямо в Игнатьево.
До Свистухи 16 км по шоссе, со скоростью 20 км/ч, время равно:
t_{1}=frac{S}{v}=frac{16}{20}=frac{4}{5}=0,8
Переведём в минуты:
0,8·60 = 48 минут
Далее по прямой тропинке СИ мимо пруда, это гипотенуза прямоугольного треугольника СИБ. Найдём СБ:
СБ = НБ – НС = 36 – 16 = 20 км
По теореме Пифагора найдём СИ:
СИ2 = СБ2 + БИ2
СИ2 = 202 + 152
СИ2 = 400 + 225
СИ2 = 625
СИ = √625 = 25 км
Это лестная тропа, скорость тут 15 км/ч, тогда время:
t_{2}=frac{S}{v}=frac{25}{15}=frac{5}{3}
Переведём в минуты:
frac{5}{3}cdot 60=100
Всего времени они потратят на 3-ю дорогу:
48 + 100 = 148 минут
Это наименьшее время.
Ответ: 148.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.9 / 5. Количество оценок: 12
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Слайд 1
Математика
Модель ОГЭ — 2020
Практические задачи
Титова Л.А.

Слайд 2Основные изменения в структуре ОГЭ-2020
изменения в ОГЭ плавные и
поэтапные
ОГЭ будет проходить по новому ФГОС
исчезновение модулей «алгебра» и «геометрия»
появление «практических задач»
www.fipi.ru

Слайд 3Практические задачи
реальные жизненные ситуации
одна ситуация объединяет в себе
несколько задач
адресованы тем, кто не пойдёт в старшую школу
содержат акценты на сложности, встречающиеся в 10-11 классах
www.fipi.ru

Слайд 4Практические задачи
распознавание объектов
простейшие задачи вычислительного характера
вычисление площади фигуры (или
сравнение площадей фигур)
вычисление длины отрезка
задача на оптимальный выбор

Слайд 5Задача 1
01.10.2019
1. Для объектов, указанных в таблице, определите, какими цифрами
они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность
четырёх цифр.
При входе на участок напротив ворот находится гараж, а за гаражом – жилой дом. Площадь, занятая гаражом, равна 48 кв. м. Слева от ворот находится большой газон, отмеченный на плане цифрой 5. На газоне имеются круглый бассейн, беседка и две ромбовидные клумбы. Беседка отмечена на плане цифрой 4. При въезде на участок имеется площадка, вымощенная тротуарной плиткой размером 0,2 м х 0,1 м и обозначенная на плане цифрой 7.
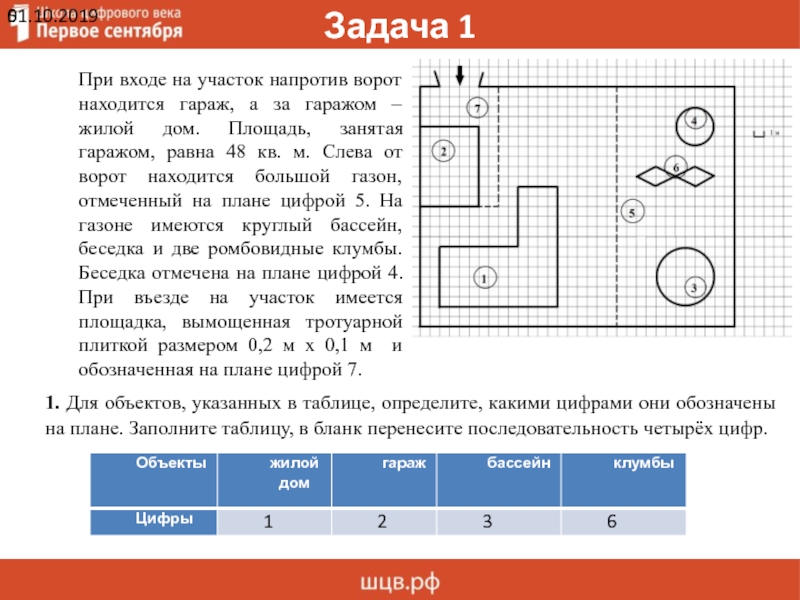
Слайд 6Задача 1
2. Найдите площадь, которую занимает одна клумба. Ответ дайте
в квадратных метрах.
Ответ: 4

Слайд 7Задача 1
3. Тротуарная плитка продаётся в упаковках по 45 штук.
Сколько упаковок плитки понадобилось, чтобы выложить площадку перед гаражом?
Ответ: 54
Слайд 8Задача 1
4. Во сколько раз площадь бассейна больше площади беседки?
Ответ:
2,25
Слайд 9Задача 1
5. Хозяин участка хочет обновить газон к новому дачному
сезону. Для этого он планирует купить семена газонной травы. Цена
одной упаковки семян, её масса и рекомендуемый расход указаны в таблице.
Во сколько рублей обойдётся наиболее дешёвый вариант? (Территорию, занятую бассейном и беседкой, засевать не предполагается. Клумбы планируется убрать и на их месте тоже засеять газонную траву. Число возьмите равным 3.)
Слайд 10Задача 1
Решение:
24*12-27-12=249 (кв. м.) – площадь, которую нужно засеять
4*500=2000 (руб.)
– стоимость варианта «А»
7*330=2310 (руб.) – стоимость варианта «Б»
6*340=2040 (руб.)
– стоимость варианта «В»
8*290=2320 (руб.) – стоимость варианта «Г»
Ответ: 2000
Слайд 11Задача 2
1. Для объектов, указанных в таблице, определите, какими цифрами
они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность
четырёх цифр.
На рисунке изображен план однокомнатной квартиры в 16-этажном жилом доме (сторона каждой клетки на плане равна 0,5 м). Окна квартиры выходят на север. При входе в квартиру располагается прихожая. Справа от прихожей находится санузел, а слева – вход в комнату. Санузел имеет общую стену с кухней, отмеченную на плане цифрой 2. Комната имеет наибольшую площадь из всех помещений. Из кухни есть выход на балкон. Пол санузла выложен плиткой размером 25смх25см.

Слайд 12Задача 2
2. Плитка для пола продается в упаковках по 8
штук. Сколько упаковок плитки понадобилось, чтобы выложить пол санузла?
Ответ: 8

Слайд 13Задача 2
3. Найдите площадь, которую занимает балкон. Ответ дайте в
квадратных метрах.
Ответ: 3
Слайд 14Задача 2
4. Во сколько раз площадь прихожей меньше, чем площадь
комнаты?
Ответ: 4
Слайд 15Задача 2
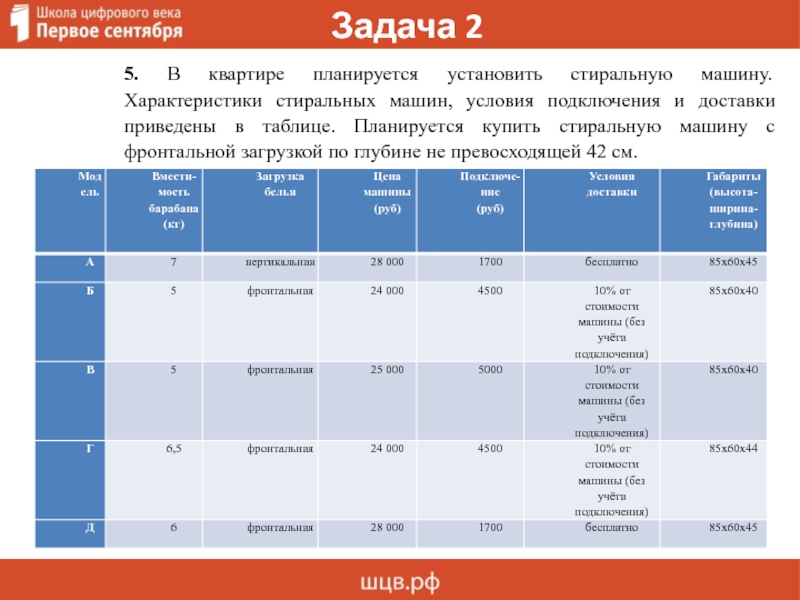
5. В квартире планируется установить стиральную машину. Характеристики стиральных
машин, условия подключения и доставки приведены в таблице. Планируется купить
стиральную машину с фронтальной загрузкой по глубине не превосходящей 42 см.
Слайд 16Задача 2
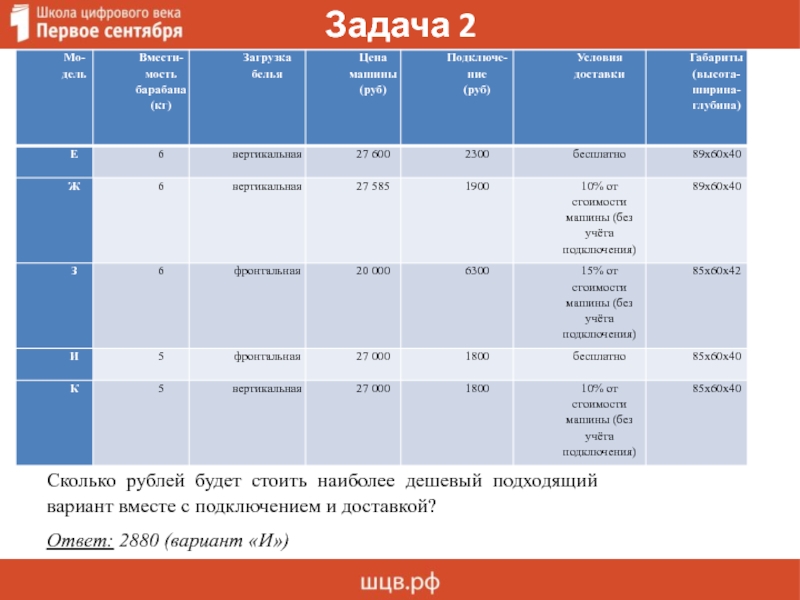
Сколько рублей будет стоить наиболее дешевый подходящий вариант вместе
с подключением и доставкой?
Ответ: 2880 (вариант «И»)
Слайд 17Задача 3
На рисунке изображён план однокомнатной квартиры в 16-этажном жилом
доме (сторона каждой клетки на плане равна 0,4 м). Окна
квартиры выходят на север. При входе в квартиру располагается прихожая. Справа от прихожей находится санузел, а слева – вход в комнату. Санузел имеет общую стену с кухней, отмеченную на плане цифрой 5. Комната имеет наибольшую площадь из всех помещений, из неё есть выход на просторную лоджию. Пол лоджии выложен плиткой размером 20смх20см.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырёх цифр.

Слайд 18Задача 3
2. Плитка для пола продаётся в упаковках по 10
штук. Сколько упаковок плитки понадобилось, чтобы выложить пол лоджии?
Ответ: 17
Слайд 19Задача 3
3. Найдите площадь, которую занимает санузел. Ответ дайте в
квадратных метрах.
Ответ: 5,04

Слайд 20Задача 3
4. Найдите расстояние между противоположными углами кухни (длину диагонали)
в метрах.
Ответ: 4
Слайд 21Задача 3
5. В квартире планируется заменить электрическую плиту. Характеристики электроплит,
условия подключения и доставки приведены в таблице. Планируется купить электрическую
плиту с максимальной температурой не менее 275оС и глубиной 60 см.
Слайд 22Задача 3
Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе
с подключением и доставкой?
Ответ: 23190 (Вариант «И»)
Слайд 23Задача 4
На графике точками изображено количество минут, потраченных на исходящие
вызовы, и количество гигабайтов мобильного интернета, израсходованных абонентом в процессе
пользования смартфоном, за каждый месяц 2018 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.

Слайд 24Задача 4
Определите, какие месяцы соответствуют указанному в таблице количеству израсходованных
гигабайтов. Заполните таблицу, в ответ запишите подряд числа, соответствующие номерам
месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев май, январь, ноябрь, август в ответ нужно записать число 51118).
Сколько рублей потратил абонент на услуги связи в сентябре?
Ответ: 475

Слайд 25Задача 4
В течение года абонент пользовался тарифом «Стандартный», абонентская плата
по которому составляет 300 рублей в месяц. При условии нахождения
абонента на территории РФ в абонентскую плату тарифа «Стандартный» входит:
• пакет минут, включающий 350 минут исходящих вызовов на номера, зарегистрированные на территории РФ;
• пакет интернета, включающий 3,5 гигабайта мобильного интернета;
• пакет SMS, включающий 150 SMS в месяц;
• безлимитные бесплатные входящие вызовы.
Стоимость минут, интернета и SMS сверх пакета указана в таблице.
Абонент не пользовался услугами связи в роуминге и не звонил на номера, зарегистрированные за рубежом. За весь год абонент отправил 120 SMS.
3. Сколько месяцев в 2018 году абонент не превышал лимит по пакету исходящих минут?
Ответ: 10

Слайд 26Задача 4
4. Сколько месяцев в 2018 году абонент не превышал
лимит ни по пакету минут, ни по пакету мобильного интернета?
Ответ:
8
Слайд 27Задача 4
5. В конце 2018 года оператор связи предложил абоненту
перейти на новый тариф. Его условия приведены в таблице.
*исходящие вызовы
на номера, зарегистрированные на территории РФ
Абонент решает, перейти ли ему на новый тариф, посчитав, сколько бы он потратил на услуги связи за 2018 г., если бы пользовался им. Если получится меньше, чем он потратил фактически за 2018 г., то абонент примет решение сменить тариф.
Перейдёт ли абонент на новый тариф?
В ответе запишите ежемесячную абонентскую плату по тарифу, который выберет абонент на 2019 год.
Ответ: 300

Слайд 28Задача 5
Иван Викторович решил построить на дачном участке теплицу длиной
NP=4 м. Для этого он сделал прямоугольный фундамент. Для каркаса
теплицы Иван Викторович заказывает металлические дуги в форме полуокружностей длиной 4,8 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B – соответственно середины отрезков MO и ON.
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
Ответ: 8

Слайд 29Задача 5
Иван Викторович решил построить на дачном участке теплицу длиной
NP=4 м. Для этого он сделал прямоугольный фундамент. Для каркаса
теплицы Иван Викторович заказывает металлические дуги в форме полуокружностей длиной 4,8 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B – соответственно середины отрезков MO и ON.
Найдите примерную ширину MN теплицы в сантиметрах. Число возьмите равным 3.
Ответ: 320

Слайд 30Задача 5
Иван Викторович решил построить на дачном участке теплицу длиной
NP=4 м. Для этого он сделал прямоугольный фундамент. Для каркаса
теплицы Иван Викторович заказывает металлические дуги в форме полуокружностей длиной 4,8 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B – соответственно середины отрезков MO и ON.
Найдите примерную площадь участка внутри теплицы в квадратных метрах. Число возьмите равным 3.
Ответ: 12,8

Слайд 31Задача 5
Иван Викторович решил построить на дачном участке теплицу длиной
NP=4 м. Для этого он сделал прямоугольный фундамент. Для каркаса
теплицы Иван Викторович заказывает металлические дуги в форме полуокружностей длиной 4,8 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B – соответственно середины отрезков MO и ON.
Сколько квадратных метров плёнки нужно купить для передней и задней стенок, если с учётом крепежа её нужно покупать с запасом 10%? Число возьмите равным 3. Результат округлите до десятых.
Ответ: 8,4

Слайд 32Задача 5
Иван Викторович решил построить на дачном участке теплицу длиной
NP=4 м. Для этого он сделал прямоугольный фундамент. Для каркаса
теплицы Иван Викторович заказывает металлические дуги в форме полуокружностей длиной 4,8 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B – соответственно середины отрезков MO и ON.
Найдите примерную высоту входа в теплицу в сантиметрах. Число возьмите равным 3. Результат округлите до целых.
Ответ: 139

Слайд 33Задача 6
Миша летом отдыхает у дедушки в деревне Кузьминки. В
субботу они собираются съездить на велосипедах в село Борисово в
магазин. Из Кузьминок в Борисово можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Соловьи до деревни Подлипки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Борисово. Есть и третий маршрут: в Соловьях можно свернуть на прямую тропинку, которая идёт мимо пруда прямо в Борисово.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.

Слайд 34Задача 6
По шоссе Миша с дедушкой едут со скоростью 20
км/ч, а по лесной дорожке и тропинке – 13 км/ч. Расстояние
по шоссе от Кузьминок до Соловьев равно 11 км, от Кузьминок до Подлипок – 16 км, а от Подлипок до Борисово ещё 12 км (см. рисунок).
2. Сколько километров проедут Миша с дедушкой, если они поедут по шоссе через Подлипки?
Ответ: 28
Слайд 35Задача 6
По шоссе Миша с дедушкой едут со скоростью 20
км/ч, а по лесной дорожке и тропинке – 13 км/ч. Расстояние
по шоссе от Кузьминок до Соловьев равно 11 км, от Кузьминок до Подлипок – 16 км, а от Подлипок до Борисово ещё 12 км (см. рисунок).
3. Найдите расстояние от д. Кузьминки до с. Борисово по прямой. Ответ выразите в километрах.
Ответ: 20

Слайд 36Задача 6
По шоссе Миша с дедушкой едут со скоростью 20
км/ч, а по лесной дорожке и тропинке – 13 км/ч. Расстояние
по шоссе от Кузьминок до Соловьев равно 11 км, от Кузьминок до Подлипок – 16 км, а от Подлипок до Борисово ещё 12 км (см. рисунок).
4. Сколько времени затратят на дорогу Миша с дедушкой, если поедут через Подлипки? Ответ выразите в минутах.
Ответ: 84

Слайд 37Задача 6
По шоссе Миша с дедушкой едут со скоростью 20
км/ч, а по лесной дорожке и тропинке – 13 км/ч. Расстояние
по шоссе от Кузьминок до Соловьев равно 11 км, от Кузьминок до Подлипок – 16 км, а от Подлипок до Борисово ещё 12 км (см. рисунок).
5. Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Миша с дедушкой, если поедут этим маршрутом?
Ответ: 84
Слайд 38Итог
Основная задача – развитие умения получать пользу от математики в
повседневных ситуациях.
Появление геометрических сюжетов, где необходимы вычислительные навыки. Особенно
важно – площади и длины.
Естественные задачи на проценты (вычисление платежей, скидок, наценок и т.п.)
Появление оптимизационных задач (время, платежи, распределение ресурсов)
Появление простейших задач на представление и анализ данных (диаграммы, таблицы)

Слайд 39Контакты издательства «Интеллект-центр»
Адрес: 125445, г. Москва,
Ул. Смольная, д. 24А,
офис 712
Телефон: +7 (495) 660-34-53
Email: intellect@izentr.ru
Сайт: https://www.intellectcentre.ru/

ОГЭ математика
141 вариант
1. Пользуясь описанием, определите, какими цифрами на плане
обозначены населённые пункты. В ответе запишите полученную последовательность
четырёх цифр.
|
Населённые |
Дубёнки |
Бережки |
Ушаково |
Афонино |
|
Цифры |
Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они
собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно
проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через
деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево
на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки
можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село
Бережки.
По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по
грунтовой дороге —50 км/ч. На плане изображено взаимное расположение населённых
пунктов, сторона каждой клетки равна 2 км.
2. Найдите расстояние от деревни Ушаково до села Бережки по прямой.
Ответ выразите в километрах.
3. Сколько километров проедут Гриша с дедушкой, если они поедут по
шоссе через Афонино?
4. Сколько времени затратят на дорогу Гриша с дедушкой, если они
поедут сначала до деревни Дубёнки, а затем свернут на грунтовую дорогу, идущую
мимо озера? Ответ выразите в минутах.
5. Определите, на какой маршрут потребуется меньше всего времени. В
ответе укажите, сколько минут потратят на дорогу Гриша с дедушкой, если поедут
этим маршрутом.
6.
Найдите значение выражения 3,8 + 2,9.
7. На координатной прямой отмечены числа .
Какое из следующих утверждений неверно?
1)
2)
3)
4)
8. Найдите значение выражения при
9. Найдите корень уравнения −5 + 9x = 10x +
4.
10. В таблице представлены результаты четырёх стрелков, показанные ими
на тренировке.
|
Номер стрелка |
Число выстрелов |
Число попаданий |
|
1 |
42 |
28 |
|
2 |
70 |
20 |
|
3 |
54 |
45 |
|
4 |
46 |
42 |
Тренер решил послать на соревнования того стрелка, у которого
относительная частота попаданий выше. Кого из стрелков выберет тренер? Укажите
в ответе его номер.
11. Установите соответствие между графиками функций и формулами,
которые их задают.
ГРАФИКИ ФУНКЦИЙ
ФОРМУЛЫ
1)
2)
3)
В таблице под каждой буквой укажите соответствующий номер.
12. Период колебания математического маятника (в
секундах) приближенно можно вычислить по формуле , где
—
длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в
метрах), период колебаний которого составляет 3 секунды.
13. Решите неравенство
1) [-8;8]
2)
3) нет решений
4)
14. Бригада рабочих могла выполнить всю работу за 24 ч, если бы
работали одновременно все рабочие. однако по плану в первый час работал один
рабочий, во второй час — 2 рабочих, в третий — 3 и т. д. до тех пор, пока в
работу не включились все рабочие. И только несколько часов перед завершением
работала вся бригада. Время работы, предусмотренное планом, было бы сокращено
на 6 часов, если бы с самого начала работы работала бы вся бригада, за
исключением пяти рабочих. Найдите количество рабочих.
15.
Найдите больший угол равнобедренной трапеции , если
диагональ образует с основанием
и
боковой стороной углы, равные 17° и 23°
соответственно. Ответ дайте в градусах.
16.
Касательные в точках A и B к
окружности с центром O пересекаются под углом 12°. Найдите
угол ABO. Ответ дайте в градусах.
17. 
квадрата равен 24. Найдите площадь квадрата.
18. 
бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
19. Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120°, то смежный с ним равен 120°.
3) Если расстояние от точки до прямой больше 3, то и длина любой
наклонной, проведённой из данной точки к прямой, больше 3.
Если
утверждений несколько, запишите их номера в порядке возрастания.
20. Решите уравнение
21. Моторная лодка прошла против течения реки 77 км и вернулась в
пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь
против течения. Найдите скорость лодки в неподвижной воде, если скорость течения
реки равна 4 км/ч.
22. Постройте график функции
и
определите, при каких значениях прямая
будет иметь с
графиком единственную общую точку.
23. В прямоугольном треугольнике с прямым
углом известны катеты:
,
. Найдите
медиану этого треугольника.
24. В окружности через середину O хорды BD проведена
хорда AC так, что дуги AB и CD равны.
Докажите, что O — середина хорды AC.
25. Медиана BM и биссектриса AP треугольника ABC пересекаются
в точке K, длина стороны AC втрое больше длины стороны AB.
Найдите отношение площади треугольника AKM к площади
четырёхугольника KPCM.
Решение
1. Пользуясь описанием, определите, какими цифрами на плане
обозначены населённые пункты. В ответе запишите полученную последовательность
четырёх цифр.
|
Населённые |
Дубёнки |
Бережки |
Ушаково |
Афонино |
|
Цифры |
Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они
собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно
проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через
деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево
на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки
можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село
Бережки.
По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по
грунтовой дороге —50 км/ч. На плане изображено взаимное расположение населённых
пунктов, сторона каждой клетки равна 2 км.
Решение.
Пользуясь описанием и рисунком можно заметить, что деревня Дубенки
соответствует цифре 2, деревня Бережки — цифре 4, деревня Ушаково — цифре 3 и
деревня Афонино —цифре 1.
Ответ: 2431.
2. Найдите расстояние от деревни Ушаково до села Бережки по прямой.
Ответ выразите в километрах.
Решение.
Расстояние от деревни Ушаково до села Бережки соответствует длине
гипотенузы прямоугольного треугольника с катетами 30 и 16. По теореме Пифагора
имеем:
Ответ: 34.
3. Сколько километров проедут Гриша с дедушкой, если они поедут по
шоссе через Афонино?
Решение.
Расстояние, которое проедут Гриша с дедушкой, проезжая через
Афонино, равно сумме длин катетов прямоугольного треугольника с катетами 30 и
16. Таким образом, имеем, что искомое расстояние равно 30 + 16 = 46.
Ответ: 46.
4. Сколько времени затратят на дорогу Гриша с дедушкой, если они
поедут сначала до деревни Дубёнки, а затем свернут на грунтовую дорогу, идущую
мимо озера? Ответ выразите в минутах.
Решение.
По шоссе Гриша с дедушкой проедут 18 километров со скоростью 60
км/ч. Следовательно, они затратят 18 : 60 = 0,3 часа или 18 минут. Дальше по
условию задачи они свернут на грунтовую дорогу длина которой равна длине
гипотенузы прямоугольного треугольника с катетами 12 и 16. Таким образом, по
теореме Пифагора длина составит:
По грунтовой дороге Гриша с дедушкой едут со скоростью 50 км/ч,
следовательно они затратят 20 : 50 = 0,4 часа или 24 минуты.
Таким образом, Гриша с дедушкой на весь путь затратят 24 + 18 = 42
минуты.
Ответ: 42.
5. Определите, на какой маршрут потребуется меньше всего времени. В
ответе укажите, сколько минут потратят на дорогу Гриша с дедушкой, если поедут
этим маршрутом.
Решение.
Гриша с дедушкой могут поехать тремя разными маршрутами.
Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути равна длине
гипотенузы прямоугольного треугольника с катетами 30 и 16. По теореме Пифагора
имеем:
Двигаясь по грунтовой дороге со скоростью 50 км/ч дедушка с Гришой
потратят 34 : 50 = 0,68 часа или 40,8 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По
шоссе Гриша с дедушкой проедут 18 километров со скоростью 60 км/ч.
Следовательно, они затратят 18 : 60 = 0,3 часа или 18 минут. Дальше по условию
задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы
прямоугольного треугольника с катетами 12 и 16. Таким образом, по теореме
Пифагора длина составит:
По грунтовой дороге Гриша с дедушкой едут со скоростью 50 км/ч,
следовательно они затратят 20 : 50 = 0,4 часа или 24 минуты.
Таким образом, Гриша с дедушкой на весь путь затратят 24 + 18 = 42
минуты.
3) По шоссе через Афонино. Расстояние, которое проедут Гриша с
дедушкой, проезжая через Афонино, равно сумме длин катетов прямоугольного
треугольника с катетами 30 и 16. Таким образом, имеем, что искомое расстояние
равно 30 + 16 = 46.
Двигаясь по шоссе со скоростью 60 км/ч Гриша с дедушкой потратят
46 : 60 часа или 46 минут.
Таким образом, самый быстрый путь составит 40,8 минут.
Ответ: 40,8.
6.
Найдите значение выражения 3,8 + 2,9.
Решение.
Найдем значение выражения: 3,8 + 2,9 = 6,7.
Ответ: 6,7.
7. На координатной прямой отмечены числа .
Какое из следующих утверждений неверно?
1)
2)
3)
4)
Решение.
Заметим, что
и
Проверим все варианты ответа:
1) — верно, так
как , а
2) — неверно: так
как и
, имеем:
3) — верно, так как
а
4) — верно, так
как а
Ответ указан под номером 2.
8. Найдите значение выражения при
Решение.
Преобразуем выражение:
Подставим значение
Ответ: −0,2.
9. Найдите корень уравнения −5 + 9x = 10x +
4.
Решение.
Последовательно получаем:
Ответ: −9.
10. В таблице представлены результаты четырёх стрелков, показанные ими
на тренировке.
|
Номер стрелка |
Число выстрелов |
Число попаданий |
|
1 |
42 |
28 |
|
2 |
70 |
20 |
|
3 |
54 |
45 |
|
4 |
46 |
42 |
Тренер решил послать на соревнования того стрелка, у которого
относительная частота попаданий выше. Кого из стрелков выберет тренер? Укажите
в ответе его номер.
Решение.
Найдём относительную частоту попаданий каждого из стрелков:
Заметим, что Приведём
и
к общему знаменателю и
сравним: Таким
образом, наибольшая относительная частота попаданий у четвёртого стрелка.
Ответ: 4.
11. Установите соответствие между графиками функций и формулами,
которые их задают.
ГРАФИКИ ФУНКЦИЙ
ФОРМУЛЫ
1)
2)
3)
В таблице под каждой буквой укажите соответствующий номер.
Решение.
Напомним, что если прямая задана уравнением ,
то: при тангенс угла наклона
прямой к оси абсцисс положителен.
Уравнение задает прямую,
которая пересекает ось ординат в точке 3. Ее график изображен на рисунке Б).
Уравнение задает прямую, которая
пересекает ось ординат в точке 0. Ее график изображен на рисунке A).
Уравнение задает прямую, которая
пересекает ось ординат в точке -3. Ее график изображен на рисунке B).
Тем самым, искомое соответствие: А — 2, Б — 1, В — 3.
Ответ: 213.
12. Период колебания математического маятника (в
секундах) приближенно можно вычислить по формуле ,
где — длина нити (в метрах). Пользуясь этой формулой, найдите длину
нити маятника (в метрах), период колебаний которого составляет 3 секунды.
Решение.
Подставим в формулу значение :
Ответ: 2,25.
13. Решите неравенство
1) [-8;8]
2)
3) нет решений
4)
Решение.
Решим неравенство: Корнями уравнения
являются числа -8 и 8. Поэтому
Ответ: 2
14. Бригада рабочих могла выполнить всю работу за 24 ч, если бы
работали одновременно все рабочие. однако по плану в первый час работал один
рабочий, во второй час — 2 рабочих, в третий — 3 и т. д. до тех пор, пока в
работу не включились все рабочие. И только несколько часов перед завершением
работала вся бригада. Время работы, предусмотренное планом, было бы сокращено
на 6 часов, если бы с самого начала работы работала бы вся бригада, за
исключением пяти рабочих. Найдите количество рабочих.
Решение.
Пусть всего было n рабочих, тогда объем работы
составляет 24n (считаем, что за 1 час один рабочий выполняет
единицу объема работы). Пусть также время работы по плану составляло x часов.
Тогда:
Найдем количество рабочих из уравнения Получаем:
Ответ: 25 рабочих.
15.
Найдите больший угол равнобедренной трапеции , если
диагональ образует с основанием
и
боковой стороной углы, равные 17° и 23°
соответственно. Ответ дайте в градусах.
Решение.
В равнобедренной трапеции углы при основаниях равны. Угол ABC —
тупой, а угол BAD — острый, значит, ∠ABC — больший угол
равнобедренной трапеции. Углы CAD и BCA равны
как накрест лежащие. Тогда:
Ответ: 140
16.
Касательные в точках A и B к
окружности с центром O пересекаются под углом 12°. Найдите
угол ABO. Ответ дайте в градусах.
Решение.
Введём обозначение, как показано на рисунке. Касательные,
проведённые к окружности из одной точки равны, поэтому следовательно,
треугольник — равнобедренный. Откуда
Угол
между касательной и хордой равен половине дуги, которую он заключает, значит,
дуга равна 168°. Угол AOB — центральный, поэтому он
равен дуге, на которую опирается, следовательно, равен 168°. Рассмотрим
треугольник AOB, он равнобедренный, следовательно,
Ответ: 6.
17. 
квадрата равен 24. Найдите площадь квадрата.
Решение.
Периметр квадрата равен сумме длин всех его сторон. Таким образом,
сторона квадрата равна 6. Площадь квадрата равна квадрату его стороны, поэтому
она равна 36.
Ответ: 36.
18. 
бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
Решение.

треугольника равна половине произведения основания на высоту, проведенную к
данному основанию. Таким образом:
Ответ: 15
19. Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120°, то смежный с ним равен 120°.
3) Если расстояние от точки до прямой больше 3, то и длина любой
наклонной, проведённой из данной точки к прямой, больше 3.
Если
утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Любые три прямые имеют не более одной общей точки» — верно.
Если прямые имеют две и более общих точек, то они совпадают. (См. комментарии к
задаче.)
2) «Если угол равен 120°, то смежный с ним равен 120°» — неверно.
Сумма смежных углов равна 180°.
3) «Если расстояние от точки до прямой больше 3, то и длина любой
наклонной, проведённой из данной точки к прямой, больше 3» — верно.
Т. к. расстояние — длина кратчайшего отрезка до прямой, а все наклонные —
длиннее.
Ответ: 13.
20. Решите уравнение
Решение.
Последовательно получаем:
Ответ: −8; −5.
21. Моторная лодка прошла против течения реки 77 км и вернулась в
пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против
течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки
равна 4 км/ч.
Решение.
Пусть км/ч — скорость лодки в неподвижной
воде, тогда км/ч — скорость лодки
против течения реки, а км/ч — скорость лодки
по течению. Лодка затратила на путь по течению реки на 2 часа меньше, чем
против течения, составим уравнение:
Корень −18 не подходит по условию задачи, следовательно, скорость
моторной лодки в стоячей воде равна 18 км/ч.
Ответ: 18.
22. Постройте график функции
и
определите, при каких значениях прямая
будет иметь с
графиком единственную общую точку.
Решение.
Построим график функции (см. рисунок).
Из графика видно, что прямая будет иметь с
графиком функции единственную точку пересечения при принадлежащем
множеству (−1; 0].
Ответ: (−1; 0].
23. В прямоугольном треугольнике с прямым
углом известны катеты:
,
.
Найдите медиану этого треугольника.
Решение.
Медиана, проведенная к гипотенузе, равна её половине:
Ответ: 5.
24. В окружности через середину O хорды BD проведена
хорда AC так, что дуги AB и CD равны.
Докажите, что O — середина хорды AC.
Решение.
Вписанные углы ADB, CBD , ACB и DAC опираются
на равные дуги, значит, они равны.
Получаем, что треугольники СOВ и AOD подобны
по двум углам; их коэффициент подобия равен BO:OD. Поскольку BO
= OD , эти треугольники равны, следовательно, AO = OC.
25. Медиана BM и биссектриса AP треугольника ABC пересекаются
в точке K, длина стороны AC втрое больше длины
стороны AB. Найдите отношение площади треугольника AKM к
площади четырёхугольника KPCM.
Решение.
Пусть площадь треугольника равна
Медиана
делит треугольник на два равновеликих треугольника, поэтому Биссектриса
делит площадь треугольника пропорционально прилежащим сторонам, то есть:
Откуда
Рассмотрим
треугольник
— биссектриса,
следовательно:
Откуда
Выразим
площадь треугольника
Найдём отношение площади треугольника к
площади четырёхугольника
Ответ:
Сколько километров проедут Гриша с дедушкой, если они поедут по шоссе через Афонино?
Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село Бережки.
По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге —50 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
1
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
| Населённые пункты | Дубёнки | Бережки | Ушаково | Афонино |
|---|---|---|---|---|
| Цифры |
2
Найдите расстояние от деревни Ушаково до села Бережки по прямой. Ответ выразите в километрах.
3
Сколько времени затратят на дорогу Гриша с дедушкой, если они поедут сначала до деревни Дубёнки, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.
4
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гриша с дедушкой, если поедут этим маршрутом.
Спрятать решение
Решение.
Расстояние, которое проедут Гриша с дедушкой, проезжая через Афонино, равно сумме длин катетов прямоугольного треугольника с катетами 30 и 16. Таким образом, имеем, что искомое расстояние равно 30 + 16 = 46.
Ответ: 46.