Преподаватель который помогает студентам и школьникам в учёбе.
 |
 |
Алгебра |
 |
 |
Решение задачи |
 |
 |
18 февраля 2021 |
 |
 |
Выполнен, номер заказа №16224 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
245 руб. |
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!
Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):
Страховая компания заключила 40000 договоров. Вероятность страхового случая по каждому из них в течение года составляет 0,02. Найти вероятность того, что таких случаев будет более 1000. . Найти вероятность того, что таких случаев будет от 828 до 870.
Решение
Применим интегральную теорему Лапласа. Если вероятность 𝑝 наступления события 𝐴 в каждом из 𝑛 независимых испытаний постоянна и отлична от нуля и единицы, то вероятность того, что в 𝑛 независимых испытаниях событие 𝐴 наступит не менее чем 𝑚1 раз и не более чем 𝑚2 раза, определяется по формуле: где Ф(𝑥) – функция Лапласа. В каждом случае Вероятность события 𝐴 – число страховых случаев будет более 1000, равна: Вероятность события 𝐵 – число страховых случаев будет от 828 до 870, равна:
Похожие готовые решения по алгебре:
- Автомобильная сигнализация срабатывает в среднем в 95 случаях из 100. Найти вероятность того, что в 150 случаях сигнализация
- Два игральных кубика подбрасывают 810 раз. Найдите вероятность того, что сумма очков на двух кубиках
- На сцене выступают 65 скрипачей. Вероятность того, что у скрипки порвется струна, равна
- 45% студентов первых курсов в среднем выполняют контрольные работы в срок. Какова вероятность того
- Всхожесть семян оценивается вероятностью 0,85. Найдите вероятность того, что из 500 высеянных семян взойдет
- Каждый из 300 компьютеров в интернет-кафе занят клиентом в среднем в 85% рабочего времени. Какова вероятность того
- Испытываются 600 одинаковых деталей, а вероятность того, что каждая деталь выдержит испытание, равна
- Завод выпускает новую модель приборов регистрации, для которой вероятность отказа в течение гарантийного срока
- Вероятность того, что пара обуви, взятая наудачу из изготовленной партии, окажется высшего сорта
- В семье 4 ребенка. Найти вероятность того, что среди них 1 девочка
- Вероятность наступления некоторого события в каждом из 200 независимых испытаний равна
- Вероятность появления события в каждом из 𝑛 независимых испытаний равна 𝑝.
Задача
1.
Игральная кость брошена 6 раз. Найти
вероятность того, что ровно 3 раза выпадет
«шестерка».
Решение.
Шестикратное бросание кости можно
рассматривать как последовательность
независимых испытаний с вероятностью
успеха («шестерки»), равной 1/6, и
вероятностью неудачи — 5/6. Искомую
вероятность вычисляем по формуле
.
Задача 2. Монета бросается 6 раз.
Найти вероятность того, что герб выпадет
не более, чем 2 раза.
Решение.Искомая вероятность равна
сумме вероятностей трех событий,
состоящих в том, что герб не выпадет ни
разу, либо один раз, либо два раза:
Р(А) = Р6(0) + Р6(1) + Р6(2) =.
Задача
3. Аудитор
обнаруживает финансовые нарушения у
проверяемой фирмы с вероятностью 0,9.
Найти вероятность того, что среди 4
фирм-нарушителей будет выявлено больше
половины.
Решение.
Событие состоит в том, что из 4
фирм-нарушителей будет выявлено три
или четыре, т.е.
.
Задача
4.
Монета подбрасывается 3 раза. Найти
наиболее вероятное число успехов
(выпадений герба).
Решение.
Возможными значениями для числа успехов
в трех рассматриваемых испытаниях
являются m = 0, 1, 2 или 3. Пусть Am
— событие, состоящее в том, что при трех
подбрасываниях монеты герб появляется
m раз. По формуле Бернулли легко найти
вероятности событий Am
(см. таблицу):
-
m
0
1
2
3
Pn(m)
1/8
3/8
3/8
1/8
Из
этой таблицы видно, что наиболее
вероятными значениями являются числа
1 и 2 (их вероятности равны 3/8). Этот же
результат можно получить и из теоремы
2. Действительно, n=3,
p=1/2,
q=1/2.
Тогда
,
т.е.
.
Задача
5. В
результате каждого визита страхового
агента договор заключается с вероятностью
0,1.
Найти наивероятнейшее число заключенных
договоров после 25 визитов.
Решение.
Имеем n=10,
p=0,1,
q=0,9.
Неравенство для наиболее вероятного
числа успехов принимает вид:
250,1–0,9m*250,1+0,1
или 1,6m*2,6.
У этого неравенства только одно целое
решение, а именно, m*=2.
Задача
6. Известно,
что процент брака для некоторой детали
равен 0,5%. Контролер проверяет 1000 деталей.
Какова вероятность обнаружить ровно
три бракованные детали? Какова вероятность
обнаружить не меньше трех бракованных
деталей?
Решение.
Имеем 1000 испытаний Бернулли с вероятностью
«успеха» р=0,005. Применяя пуассоновское
приближение с λ=np=5,
получаем
1)
P1000(3);
2)
P1000(m3)=1P1000(m<3)=1[]1
,
и
Р1000(3)0,14;
Р1000(m3)0,875.
Задача
7.
Вероятность
покупки при посещении клиентом магазина
составляет р=0,75. Найти вероятность того,
что при 100 посещениях клиент совершит
покупку ровно 80 раз.
Решение.
В данном случае n=100, m=80, p=0,75, q=0,25.
Находим
,
и определяем(x)=0,2036,
тогда искомая вероятность равна
Р100(80)=.
Задача
8. Страховая
компания заключила 40000 договоров.
Вероятность страхового случая по каждому
из них в течение года составляет 2%. Найти
вероятность, что таких случаев будет
не более 870.
Решение.
По условию задачи n=40000,
p=0,02.
Находим np=800,.
Для вычисления Р(m£870)
воспользуемся интегральной теоремой
Муавра-Лапласа:
Р(0<m£870)=
Ф0(х2)
–Ф0(х1),
где
и
.
Находим по таблице
значений функции Лапласа:
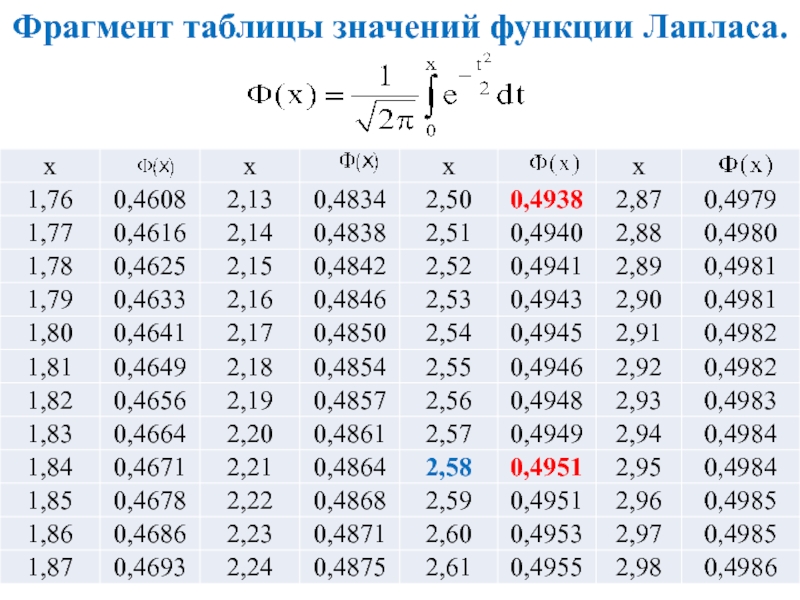
Р(0<m£870)=Ф0(х2)–Ф0(х1)=Ф0(2,5)–Ф0(–28,57)=0,4938+0,5=0,9938.
Задача
9.
Вероятность
появления события в каждом из 400
независимых испытаний равна 0,8. Найти
такое положительное число ,
чтобы с вероятностью 0,99 абсолютная
величина отклонения относительной
частоты появления события от его
вероятности не превышала .
Решение.
По условию задачи p=0,8,
n=400. Используем следствие из интегральной
теоремы Муавра-Лапласа:
.
Следовательно,.
По таблице для функции Лапласа определяем.
Отсюда=0,0516.
Задача
10. Курс
акции за день может подняться на 1 пункт
с вероятностью 50%, опуститься на 1 пункт
с вероятностью 30% и остаться неизменным
с вероятностью 20%. Найти вероятность
того, что за 5 дней торгов курс поднимется
на 2 пункта.
Решение.
Возможны
только следующие два варианта развития
событий:
1) курс растет 2
дня, ни разу не падает, не меняется 3 дня;
2) курс растет 3
дня, падает 1 день, не меняется 1 день.
Таким образом,
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача № 1. Страховая компания планирует заключить 40 000 договоров
страхования имущества. Вероятность наступления страхового случая 0,02. Средняя
страховая сумма 1 000 000 руб. Среднее страховое возмещение при наступлении
страхового события 800 000 руб. Данных о разбросе возможных страховых возмещений
нет. Возможные страховые возмещения не должны превысить собранных страховых
премий с вероятностью 0,95. Доля нагрузки в структуре страхового тарифа 25%.
Рассчитать страховой тариф (брутто—ставка).
Количество договоров= 40000
Вероятность страхового случая = 0,02
Средняя страховая сумма= 1000000
Среднее возмещение= 800000
Дисперсии нет (рассчитываем рисковую надбавку)
Гамма= 0,95, следовательно альфа= 1,645
Доля нагрузки= 25%
1. Основная часть нетто—ставки на 100 рублей страховой суммы= 100* среднее страховое
возмещение*вероятность: средняя страховая сумма= 100*800000*0,02:1000000=1,6 (рублей)
2. Рисковая!надбавка =𝟏,𝟐∝×основная!часть!нетто −ставки!на!𝟏𝟎𝟎!рублей!страховой!суммы×
𝟏−вероятность!события :количество!договоров×вероятность!события =1,2*1,645*1,6*((1—
0,02):((40000*0,02)^(0,5)= 0,11(рублей)
3. Нетто—ставка на 100 рублей страховой суммы= основная часть нетто—ставки на 100 рублей
страховой суммы + рисковая надбавка=1,6+0,11=1,71 (рублей)
4. Брутто—ставка на 100 рублей страховой суммы= нетто—ставка на 100 рублей страховой суммы : (1—
доля нагрузки)= 1,71:(1—0,25)=2,28 (рублей)
Ответ: страховой тариф равен 2,28 рублей (с каждых 100 рублей страховой суммы страхователь
должен уплатить 2,28 рубля страховщику).
Задача № 2. Страховщик проводит коллективное страхование от несчастного
случая. По данным статистики, на 1000 застрахованных лиц приходится 50 страховых
случаев. Средняя страховая выплата – 30 тыс. рублей. Средняя страховая сумма по
договору составляет 80 тыс. рублей. Количество договоров страхования 6 000. Среднее
квадратическое отклонение страховой выплаты составляет 8 тыс. руб. Доля нагрузки в
тарифной ставке – 24%. Рассчитать страховой взнос со 100 тыс. руб. страховой суммы
при условии гарантии безопасности 0,95 (по методике Росстрахнадзора).
На 1000 застрахованных лиц приходится 50 страховых случаев
Средняя страховая выплата= 30000
Средняя страховая сумма= 80000
Количество договоров= 6000
𝜎=8000
Доля нагрузки= 24%
Страховая сумма= 100000
Гамма (условие гарантии безопасности)= 0,95, следовательно альфа= 1,645
1. Вероятность наступления страхового случая= количество страховых случаев :
количество застрахованных лиц= 50:1000= 0,05
2. Основная часть нетто—ставки на 100 рублей страховой суммы= 100* среднее страховое
возмещение*вероятность: средняя страховая сумма= 100*30000*0,05:80000=1,88 (рублей)
Решение. Имеем n=10, p=0,1, q=0,9. Неравенство для наиболее вероятного числа успехов принимает вид: 250,1–0,9m*250,1+0,1 или 1,6m*2,6. У этого неравенства только одно целое решение, а именно, m*=2.
Задача 6. Известно, что процент брака для некоторой детали равен 0,5%. Контролер проверяет 1000 деталей. Какова вероятность обнаружить ровно три бракованные детали? Какова вероятность обнаружить не меньше трех бракованных деталей?
Решение. Имеем 1000 испытаний Бернулли с вероятностью «успеха» р=0,005. Применяя пуассоновское приближение с λ=np=5, получаем
1) P1000(3) ;
2) P1000(m3)=1P1000(m<3)=1[ ]1
,
и Р1000(3)0,14; Р1000(m3)0,875.
Задача 7. Вероятность покупки при посещении клиентом магазина составляет р=0,75. Найти вероятность того, что при 100 посещениях клиент совершит покупку ровно 80 раз.
Решение. В данном случае n=100, m=80, p=0,75, q=0,25. Находим , и определяем (x)=0,2036, тогда искомая вероятность равна Р100(80)=
.
Задача 8. Страховая компания заключила 40000 договоров. Вероятность страхового случая по каждому из них в течение года составляет 2%. Найти вероятность, что таких случаев будет не более 870.
Решение. По условию задачи n=40000, p=0,02. Находим np=800, . Для вычисления Р(m£870) воспользуемся интегральной теоремой Муавра-Лапласа:
Р(0<m£870)= Ф0(х2) –Ф0(х1), где и
.
Находим по таблице значений функции Лапласа:
Р(0<m£870)=Ф0(х2)–Ф0(х1)=Ф0(2,5)–Ф0(–28,57)=0,4938+0,5=0,9938.
Задача 9. Вероятность появления события в каждом из 400 независимых испытаний равна 0,8. Найти такое положительное число , чтобы с вероятностью 0,99 абсолютная величина отклонения относительной частоты появления события от его вероятности не превышала .
Решение. По условию задачи p=0,8, n=400. Используем следствие из интегральной теоремы Муавра-Лапласа: . Следовательно,
. По таблице для функции Лапласа определяем
. Отсюда =0,0516.
Задача 10. Курс акции за день может подняться на 1 пункт с вероятностью 50%, опуститься на 1 пункт с вероятностью 30% и остаться неизменным с вероятностью 20%. Найти вероятность того, что за 5 дней торгов курс поднимется на 2 пункта.
Решение. Возможны только следующие два варианта развития событий:
1) курс растет 2 дня, ни разу не падает, не меняется 3 дня;
2) курс растет 3 дня, падает 1 день, не меняется 1 день.
Таким образом,
5. Дискретные случайные величины
Задача 1. В связке из 3 ключей только один ключ подходит к двери. Ключи перебирают до тех пор, пока не отыщется подходящий ключ. Построить закон распределения для случайной величины – числа опробованных ключей.
Решение. Число опробованных ключей может равняться 1, 2 или 3. Если испытали только один ключ, это означает, что этот первый ключ сразу подошел к двери, а вероятность такого события равна 1/3. Итак, Далее, если опробованных ключей было 2, т.е. =2, это значит, что первый ключ не подошел, а второй – подошел. Вероятность этого события равна 2/3×1/2=1/3. То есть,
Аналогично вычисляется вероятность
В результате получается следующий ряд распределения:
Задача 2. Построить функцию распределения F(x) для случайной величины из задачи 1.
Решение. Случайная величина имеет три значения 1, 2, 3, которые делят всю числовую ось на четыре промежутка: . Если x<1, то неравенство x невозможно (левее x нет значений случайной величины ) и значит, для такого x функция F(x)=0.
Если 1x<2, то неравенство x возможно только если =1, а вероятность такого события равна 1/3, поэтому для таких x функция распределения F(x)=1/3.
Если 2x<3, неравенство x означает, что или =1, или =2, поэтому в этом случае вероятность P(<x)=P(=1)+P(=2)=2/3, т.е. F(x)=2/3.
И, наконец, в случае x3 неравенство x выполняется для всех значений случайной величины , поэтому P(<x)=P(=1)+P(=2)+P(=3)=1, т.е. F(x)=1.
Итак, мы получили следующую функцию:

Задача 3. Совместный закон распределения случайных величин x и h задан c помощью таблицы
|
x h |
1 |
2 |
|
–1 |
1/16 |
3/16 |
|
0 |
1/16 |
3/16 |
|
1 |
1/8 |
3/8 |
Вычислить частные законы распределения составляющих величин x и h. Определить, зависимы ли они. Вычислить вероятность .
Решение. Частное распределение для x получается суммированием вероятностей в строках:
;
;
.
Аналогично получается частное распределение для h:
;
.
Полученные вероятности можно записать в ту же таблицу напротив соответствующих значений случайных величин:
|
x h |
1 |
2 |
px |
|
–1 |
1/16 |
3/16 |
1/4 |
|
0 |
1/16 |
3/16 |
1/4 |
|
1 |
1/8 |
3/8 |
1/2 |
|
ph |
1/4 |
3/4 |
1 |
Теперь ответим на вопрос о независимости случайных величин x и h. С этой целью для каждой клетки совместного распределения вычислим произведение (т.е. сумм по соответствующей строке и столбцу) и сравним его со значением вероятности
в этой клетке. Например, в клетке для значений x=-1 и h=1 стоит вероятность 1/16, а произведение соответствующих частных вероятностей 1/4×1/4 равно 1/16, т.е. совпадает с совместной вероятностью. Это условие так же проверяется в оставшихся пяти клетках, и оно оказывается верным во всех. Следовательно, случайные величины x и h независимы.
Заметим, что если бы наше условие нарушалось хотя бы в одной клетке, то величины следовало бы признать зависимыми.
Для вычисления вероятности отметим клетки, для которых выполнено условие
. Таких клеток всего три, и соответствующие вероятности в этих клетках равны 1/8, 3/16, 3/8. Их сумма равна 11/16, это и есть искомая вероятность. Вычисление этой вероятности можно записать так:
Задача 4. Пусть случайная величина ξ имеет следующий закон распределения:
Вычислить математическое ожидание M, дисперсию D и среднеквадратическое отклонение .
Решение. По определению математическое ожидание равно
.
Далее
,
а потому
.
Среднее квадратическое отклонение .
Задача 5. Для пары случайных величин из задачи 3 вычислить .
Решение. Воспользуемся формулой . А именно, в каждой клетке таблицы выполняем умножение соответствующих значений
и
, результат умножаем на вероятность pij, и все это суммируем по всем клеткам таблицы. В итоге получаем:
Задача 6. Для пары случайных величин из задачи 3 вычислить ковариацию cov(,).
Решение. В предыдущей задаче уже было вычислено математическое ожидание . Осталось вычислить
и
. Используя полученные в решении задачи 3 частные законы распределения, получаем
;
;
и значит,
,
чего и следовало ожидать вследствие независимости случайных величин.
Задача 7. Случайный вектор (x,h) принимает значения (0,0), (1,0), (–1,0), (0,1) и (0,–1) равновероятно. Вычислить ковариацию случайных величин x и h. Показать, что они зависимы.
Решение. Поскольку Р(x=0)=3/5, P(x=1)=1/5, P(x=–1)=1/5; Р(h=0)=3/5, P(h=1)=1/5, P(h=–1)=1/5, то Мx=3/50+1/51+1/5(–1)=0 и Мh=0;
М(xh)=0´0´1/5+1´0´1/5–1´0´1/5+0´1´1/5–0´1´1/5=0.
Получаем cov(x,h)=М(xh)–МxМh=0, и случайные величины некоррелированны. Однако они зависимы. Пусть x=1, тогда условная вероятность события {h=0} равна Р(h=0|x=1)=1 и не равна безусловной Р(h=0)=3/5, или вероятность {ξ=0,η=0} не равна произведению вероятностей: Р(x=0,h=0)=1/5¹Р(x=0)Р(h=0)=9/25. Следовательно, x и h зависимы.
Задача 8. Случайные приращения цен акций двух компаний за день и имеют совместное распределение, заданное таблицей:
|
|
1 |
+1 |
|
1 |
0,3 |
0,2 |
|
+1 |
0,1 |
0,4 |
Найти коэффициент корреляции.
Решение.Прежде всего вычисляем M=0,30,20,1+0,4=0,4. Далее находим частные законы распределения и :
|
|
1 |
+1 |
p |
|
1 |
0,3 |
0,2 |
0,5 |
|
+1 |
0,1 |
0,4 |
0,5 |
|
p |
0,4 |
0,6 |
Определяем M=0,50,5=0; M=0,60,4=0,2; D=1; D=1–0,22=0,96; cov(,)=0,4. Получаем
.
Решения задач на теоремы Лапласа
На этой странице вы найдете решения типовых задач по теории вероятностей на использование теорем Лапласа (интегральной и локальной, еще их называют формулами Муавра-Лапласа) и их следствия.
Данные приближенные формулы применяются, когда мы по-прежнему решаем задачи схемы независимых испытаний Бернулли (примеры тут), но речь идет уже об очень большом числе испытаний (стандартные условия $n>100$, $np>20$). Непосредственные вычисления по формуле Бернулли трудоемки, и мы прибегаем к удобным и простым теоремам Муавра-Лапласа.
Формулы Муавра-Лапласа
Рассмотрим $n$ независимых испытаний, в каждом из которых событие может произойти с одной и той же вероятностью $p$. Тогда при больших $n$ вероятности можно вычислять по приближенным формулам Муавра-Лапласа.
Вероятность того, что событие наступит в точности $k$ раз, можно вычислить по формуле (локальная теорема Лапласа):
Значения функции $phi (x) =frac<1><sqrt<2pi>> e^<-x^2/2>$ берутся из таблиц.
Вероятность того, что событие наступит от $k_1$ до $k_2$ раз, можно вычислить по формуле (интегральная теорема Лапласа):
$$ P(k_1 le X le k_2) approx Phi left( frac<sqrt> right) — Phi left( frac<sqrt> right) $$
Здесь $Phi(x)$ — нормированная функция Лапласа (ее значения берутся из таблиц)
Еще теорию по этой теме вы найдете в онлайн-учебнике.
Примеры решений
Локальная теорема Лапласа
Задача 1. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100 новорожденных окажется 50 мальчиков.
Задача 2. Вычислительное устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа каждого элемента за смену равна $р$. Найти вероятность, что за смену откажут $m$ элементов.
$р=0,024, m=6$.
Задача 3. На конвейер за смену поступает 300 изделий. Вероятность того, что поступившая на конвейер деталь стандартна, равна 0,75. Найти вероятность того, что стандартных деталей на конвейер за смену поступило ровно 240.
Задача 4. Вероятность поражения мишени стрелком при одном выстреле равна 0,8 Найти вероятность того, что при 100 выстрелах стрелок поразит мишень ровно 75 раз. Найти наивероятнейшее число попаданий в цель.
Задача 5. Игральную кость подбрасывают 500 раз. Какова вероятность того, что цифра 1 при этом выпадет 50 раз?
Интегральная теорема Лапласа
Задача 6. В жилом доме имеется $n$ ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что число одновременно включенных ламп будет между $m1$ и $m2$. Найти наивероятнейшее число включенных ламп среди $n$ и его соответствующую вероятность.
$n = 6400, m1 = 3120, m2 = 3200$.
Задача 7. Найти вероятность того, что если бросить монету 200 раз, то орел выпадет от 90 до 110 раз.
Задача 8. Вероятность изготовления годной детали равна 0,8. Произведено 500 деталей. Какое число годных деталей вероятнее получить: а) менее 390; б) от 390 до 410?
Задача 9. Стоматологическая клиника распространяет рекламные листовки у входа в метро. Опыт показывает, что в одном случае из тысячи следует обращение в клинику. Найти вероятность того, что при распространении 50 тыс. листков число обращений будет:
А) равно 41,
Б) находиться в границах от 36 до 47.
Задача 10. Страховая компания заключила 40000 договоров. Вероятность страхового случая по каждому из них в течение года составляет 2%. Найти вероятность, что таких случаев будет не более 870.
Решебник по теории вероятностей
Тысячи решенных и оформленных задач на формулу Лапласа и другие темы:
Применение преобразования Лапласа к решению
линейных дифференциальных уравнений и систем
1°. Общие сведения о преобразовании Лапласа: оригинал и изображение
Функцией-оригиналом называется комплекснозначная функция действительного переменного , удовлетворяющая следующим условиям:
2) функция интегрируема на любом конечном интервале оси ;
3) с возрастанием модуль функции растет не быстрее некоторой показательной функции, т. е. существуют числа 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADoAAAAQBAMAAAC1onFLAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAgUHAYqEh5RGR0VIxELEI83NdAAABBklEQVQY02NgIAAcBRWA5EVBMVRhDjUwdfq/AZCc/kUBVXa6sC2IYjNfwMDANN8AVZKxguExiGYR/sDAwOcvAGK7XIDJsgcw7D8ApFlVfzAwCM0HG8yysAEqe16AQR+kgZ3xEwNbwHqIIMvKBAgDaJY+yLJklt8MfB2foXpYTCHS8gIM+SBZR6aPDFu4P8IsZDI9AJXtB8kGsX3leMD5Ce5aJuMDEFmwyQUMnzkTuD4gZIORZNkMGJYrQkyBmgx2PdDB+hOAzhBgsDdg2C8AleSGuqp9AsP+DQwMXQIMQL/GQ8ORZSnUR5y1DOFA3/7/zyDJsB5IooYG7yvXGoz4aoAzeYQYGADRdjuTYajQpgAAAABJRU5ErkJggg==» /> и такие, что для всех имеем
Изображением функции-оригинала по Лапласу называется функция комплексного переменного , определяемая равенством
при s_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAFIAAAATBAMAAADxBkdhAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADXRSTlMAQcCBEFor0KCR6LBxSK9m8wAAAVlJREFUKM9jYCAaJBsbGx8jSqVj71LRWVuIUiqrwMB6iViVDHcT0AQNcaoUQBN0LsVh+3UGBlYlVSAnqUVaFarUASrPuKkFprJQ8JQKA0NUQmwAA0vBpZZciPnOxVClUQmzYSoXW1xyYGC7ycBewMB65DYD7waIOCtUaTHDDQY2EajtQMR8WVD6AgNj6lUGXgWoEawVYKWrpiYw9AglQFSyX2PgvGFsbMDAwHmFQXYDTKUGWOXZuwVsC1gVICqZ7jAw3wHLAl1gGwBVWAkOOja38IvMCowXoCpvMrDdYGAAKvGdwLAKotAV6szYCYzXgCovglQWMHBcZ1OYlcDWABRX4FmG6vVTCcwKTGCVsnfvKrDUWgQwX9oElJvb0ZSAGvJOmzUcOCFmgkP3IBCDDClngxjVipSEGBig7kQGLDexJg2g3zegCfFcxZ6KZoSjJ6FJShOwGwqMIwCRZlRL/vuSSQAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />. Условие 3 обеспечивает существование интеграла (2).
Преобразование (2), ставящее в соответствие оригиналу его изображение , называется преобразованием Лапласа. При этом пишут .
Свойства преобразования Лапласа
Всюду в дальнейшем считаем, что
I. Свойство линейности. Для любых комплексных постоянных и
II. Теорема подобия. Для любого постоянного 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADEAAAAQBAMAAABNQoq8AAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcGe2BFbQSGBMfCxcU2qjNsAAADDSURBVBjTY2AgDYgvxCHB5WyyALtM9wW2HUhcDgs4006A8TGyyprjAlCWiwCjCpDNekkzACLQrA6RYnwkwKgHZK42DVFghkq5CcBlAhi4NjOwPSuGGtMJlmJ/xMCgV8DA9JSB6yXc8kg3IMEKkelTAOo2gMv4Iuypm8DA+DoArgVkGiPQbdpgGdY3DDAXQP3DAPKPiAFjkRMbiqsZ1iWwPweGkY+RafYxEL8IJsHA5jklAeSShQysIHtYEaHD2JbKwAAA/gYrl5lLD9QAAAAASUVORK5CYII=» />
III. Дифференцирование оригинала. Если есть оригинал, то
Обобщение: если раз непрерывно дифференцируема на и если есть оригинал, то
IV. Дифференцирование изображения равносильно умножению оригинала на «минус аргумент», т.е.
V. Интегрирование оригинала сводится к делению изображения на
VI. Интегрирование изображения равносильно делению на оригинала:
(предполагаем, что интеграл сходится).
VII. Теорема запаздывания. Для любого положительного числа
VIII. Теорема смещения (умножение оригинала на показательную функцию). Для любого комплексного числа
IX. Теорема умножения (Э. Борель). Произведение двух изображений и также является изображением, причем
Интеграл в правой части (14) называется сверткой функций и и обозначается символом
Теорема XI утверждает, что умножение изображений равносильно свертыванию оригиналов , т.е.
Отыскание оригиналов дробно-рациональных изображений
Для нахождения оригинала по известному изображению , где есть правильная рациональная дробь, применяют следующие приемы.
1) Эту дробь разлагают на сумму простейших дробей и находят для каждой из них оригинал, пользуясь свойствами I–IX преобразования Лапласа.
2) Находят полюсы этой дроби и их кратности . Тогда оригиналом для будет функция
где сумма берется по всем полюсам функции .
В случае, если все полюсы функции простые, т.е. , последняя формула упрощается и принимает вид
Пример 1. Найти оригинал функции , если
Решение. Первый способ. Представим в виде суммы простейших дробей
и найдем неопределенные коэффициенты . Имеем
Полагая в последнем равенстве последовательно , получаем
Находя оригиналы для каждой из простейших дробей и пользуясь свойствам линейности, получаем
Второй способ. Найдем полюсы функции . Они совпадают с нулями знаменателя . Таким образом, изображение имеет четыре простых полюса . Пользуясь формулой (17), получаем оригинал
Пример 2. Найти оригинал , если .
Решение. Данная дробь имеет полюс кратности и полюс кратности . Пользуясь формулой (16), получаем оригинал
2°. Решение задачи Коши для линейных дифференциальных уравнений с постоянными коэффициентами
Пусть требуется найти решение дифференциального уравнения второго порядка с постоянными коэффициентами
Будем считать, что функция и решение вместе с его производньь ми до второго порядка включительно являются функциями-оригиналами. Пусть . По правилу дифференцирования оригиналов с учетом (2) имеем
Применяя к обеим частям (1) преобразование Лапласа и пользуясь свойством линейности преобразования, получаем операторное уравнение
Решая уравнение (20), найдем операторное решение
Находя оригинал для , получаем решение уравнения (18), удовлетворяющее начальным условиям (19).
Аналогично можно решить любое уравнение n-го порядка с постоянными коэффициентами и с начальными условиями при .
Пример 3. Решить дифференциальное уравнение операторным методом
Решение. Пусть , тогда по правилу дифференцирования оригинала имеем
Известно, что поэтому, переходя отданной задачи (21)–(22) к операторному уравнению, будем иметь
Легко видеть, что функция удовлетворяет данному уравнению и начальному условию задачи.
Пример 4. Решить уравнение .
Решение. Так как и по условию , то операторное уравнение будет иметь вид
Отсюда находим операторное решение
Разлагаем правую часть на элементарные дроби:
Переходя к оригиналам, получаем искомое решение .
Пример 5. Решить уравнение .
Решение. Так как и по условию , то операторное уравнение будет иметь вид
и, следовательно, операторное решение
Разложим правую часть на элементарные дроби:
Переходя к оригиналам, получим решение поставленной задачи
3°. Решение систем линейных дифференциальных уравнений с постоянными коэффициентами
Пусть требуется найти решение системы двух уравнений с постоянными коэффициентами
удовлетворяющее начальным условиям
Будем предполагать, что функции , а также и являются функциями-оригиналами.
По правилу дифференцирования оригиналов с учетом (24) имеем
Применяя к обеим частям каждого из уравнений системы (23) преобразование Лапласа, получим операторную систему
Эта система является линейной алгебраической системой двух уравнений с двумя неизвестными и . Решая ее, мы найдем и , а затем, переходя к оригиналам, получим решение системы (23), удовлетворяющее начальным условиям (24). Аналогично решаются линейные системы вида
Пример 6. Найти решение системы дифференциальных уравнений операторным методом
удовлетворяющее начальному условию .
Решение. Так как и , то операторная система будет иметь вид
Решая систему, получаем
Разлагаем дроби, стоящие в правых частях, на элементарные:
Переходя к оригиналам, получим искомое решение
Примеры решение задач на уравнения лапласа
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
источники:
http://mathhelpplanet.com/static.php?p=reshenie-du-i-sistem-operatornym-metodom
http://yukhym.com/ru/sluchajnye-sobytiya/lokalnaya-i-integralnaya-teoremy-laplasa.html
Слайд 1ТЕОРЕМА МУАВРА-ЛАПЛАСА
Локальная и интегральная

Слайд 2Пьер-Симо́н Лаплас (1749- 1827) — выдающийся французский математик, физик и астроном; один
из создателей теории вероятностей. Был членом Французского Географического общества.
Абрахам де Муавр (1667- 1754) — английский математик французского происхождения. Член Лондонского королевского общества (1697), Парижской (1754) и Берлинской (1735) академий наук.

Слайд 3Теорема Муавра — Лапласа — простейшая из предельных теорем теории вероятностей.
В общем
виде теорема доказана Лапласом в книге «Аналитическая теория вероятностей» (1812). Один частный случай теоремы был известен Муавру (1730), в связи с чем она и называется теоремой Муавра-Лапласа.
Утверждает, что число успехов при многократном повторении одного и того же случайного эксперимента с двумя возможными исходами приблизительно имеет нормальное распределение.

Слайд 4Рассмотрим последовательность из n независимых опытов, в каждом из которых событие A может
произойти с вероятностью p, либо не произойти — с вероятностью q = 1 − p. Обозначим через Pn(m) вероятность того, что событие A произойдет ровно m раз из n возможных. Если n будет достаточно большим, то найти значение Pn(m) по теореме Бернулли становится нереально из-за огромного объема вычислений. Локальная теорема Муавра -Лапласа позволяет найти приближенное значение вероятности.

Слайд 5Локальная теорема Муавра — Лапласа. Если в схеме Бернулли число n велико, а
число p отлично от 0 и 1, тогда:
Функция φ(x) называется функцией Гаусса. Теорема Муавра-Лапласа утверждает, что асимптотическим выражением для биномиального распределения является нормальная функция.

Слайд 6Для расчетов составлена таблица значений функции φ (x), необходимо учитывать свойства:
1. φ(−x) = φ(x) — четная, в таблице приведены значения функции лишь для положительных аргументов;
2. Функция φ(x) — монотонно убывающая. Предел φ(x) при x→∞ равен нулю.
3. Если х > 5, то можно считать, что φ(х) ≈ 0. Функция φ(х) уже при х = 5 очень мала: φ(5)=0,0000015. Поэтому таблица значений не продолжена для х > 5.

Слайд 7Пример. Вероятность покупки при посещении клиентом магазина составляет р = 0,75.
Найти вероятность, что при 100 посещениях клиент совершит покупку ровно 80 раз.
Решение. n = 100, m = 80, p = 0,75, q = 0,25.
Находим ,
определяем ϕ(1,16) = 0,2036, тогда:
Р100(80) =

Слайд 8Задание. Вероятность выпуска бракованного изделия равна 0,02. Какова вероятность того, что
среди 2500 выпущенных изделий окажется 50 бракованных
Варианты ответов:
0,1045; 2) 0,86; 3) 0,0570;
4) 0,0172; 5) 0,3989.
Ответ: пункт 5

Слайд 10Интегральная теорема Муавра – Лапласа. Если вероятность р наступления события А
в каждом испытании постоянна и отлична от 0 и 1, то вероятность, что в n независимых испытаниях (n>>1) событие А состоится число раз, заключенное в границах от а до b включительно:

Слайд 11где функция Ф (х) определяется равенством
Формула называется интегральной формулой Муавра— Лапласа.
Получаемые по интегральной и локальной формулам Муавра — Лапласа вероятности достаточно точны, если произведение nр составляет несколько сотен!!!

Слайд 12Свойства функции Ф(х)
Функция Ф(х) нечетная, Ф (- х) = — Ф(х).
Функция Ф(х) монотонно возрастающая.
Предел функции Ф(х) при x→∞ равен 0,5.
Для всех значений х > 5 считают, что Ф (х) ≈ 0,5. Уже Ф (5) = 0,4999992, при увеличении х функция Ф (х) возрастает, но не может превосходить 0,5. Поэтому в таблицах функция дана для значений х < 5.

Слайд 13Оценка отклонения относительной частоты от постоянной вероятности
Вероятность, что в n независимых
испытаниях, в каждом из которых вероятность появления события А постоянна и равна р, абсолютная величина отклонения относительной частоты появления события А от его постоянной вероятности не превысит положительного числа ε, приближенно равна:

Слайд 14Пример. Вероятность появления события в каждом из 625 независимых испытаний равна
0,8. Найти вероятность, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более, чем на 0,04.
Решение. По условию задачи: n = 625; p = 0,8; ε=0,04. Отсюда q =1– p = 0,2. Требуется найти вероятность:

Слайд 15Для решения задачи воспользуемся формулой, определяющей оценку отклонения относительной частоты от
постоянной вероятности:
Ф(х) – интегральная функция Лапласа. Найдем аргумент функции Лапласа:
По табл. функции Лапласа: Ф(2,5) = 0,4938, т.е. 2Ф(х) = 0,9876.

Слайд 19Пример. Страховая компания заключила 40000 договоров. Вероятность страхового случая по каждому
из них в течение года составляет 2%. Найти вероятность, что таких случаев будет не более 870.
Решение. По условию задачи n = 40000, p = 0,02. Находим np = 800, . Для вычисления Р (m ≤ 870) воспользуемся интегральной теоремой Муавра-Лапласа:
Р(0 < m ≤ 870) = Ф0(х2) –Ф0(х1), где

Слайд 20Находим по таблице значений функции Лапласа:
Р(0 < m ≤ 870)
= Ф0(х2) – Ф0(х1) = Ф0(2,5) – – Ф0(–28,57) = 0,4938 + 0,5 = 0,9938.
Ответ: P = 0,9938

Слайд 21Пример. Вероятность появления события в каждом из 400 независимых испытаний равна
0,8. Найти такое положительное число ε, чтобы с вероятностью 0,99 абсолютная величина отклонения относительной частоты появления события от его вероятности не превышала ε.
Решение. По условию p = 0,8, n = 400. Используем следствие из интегральной т. Муавра-Лапласа:

Слайд 22
Следовательно,
. По таблице для
функции Лапласа определяем
Отсюда, ε = 0,0516.

Слайд 23Фрагмент таблицы значений функции Лапласа.
Sold: 0
Uploaded:
17.10.2017
Content:
teorver_1238.doc 33,5 kB
Product description
1238. The insurance company has concluded 40,000 contracts. The probability of an insured event for each of them during the year is 2%. Find the probability that there will be no more than 870 such cases.
Additional information
Detailed solution. Decorated in Microsoft Word 2003 (Quest decided to use the formula editor)
Feedback
0
| Period | |||
| 1 month | 3 months | 12 months | |
| 0 | 0 | 0 | |
| 0 | 0 | 0 |
In order to counter copyright infringement and property rights, we ask you to immediately inform us at support@plati.market the fact of such violations and to provide us with reliable information confirming your copyrights or rights of ownership. Email must contain your contact information (name, phone number, etc.)










