У работ не лежащих на критическом пути раннее время наступления больше позднего

Для расчета сетевого графика необходимо определить его параметры: продолжительность работ, продолжительность путей, сроки начала и окончания работ, резервы времени.

В сетевой модели для работы, не лежащей на критическом пути, может быть два срока начала и два срока окончания – наиболее ранний и наиболее поздний.

Раннее начало работы — самый ранний момент начала работы. Раннее начало исходных работ сетевого графика равно нулю.

Раннее окончание работы — время окончания работы, если она начата в ранний срок.

Позднее начало работы — самый поздний срок, при котором может быть начата работа без нарушения общего срока выполнения работы.

Позднее окончание работы — самый поздний момент окончания работы, при котором продолжительность критического пути не изменяется.

У работ критического пути ранние и поздние сроки начала и окончания равны между собой, поэтому не имеют резервов времени. Работы, не лежащие на критическом пути, имеют резервы времени.

Полный (общий) резерв времени — максимальное время, на которое можно увеличить продолжительность работы или перенести ее начало без увеличения продолжительности критического пути.

Свободный (частный) резерв времени — время, на которое можно увеличить продолжительность работы или перенести ее начало, не изменяя при этом раннего начала последующих работ.

25

1. Порядок сетевого планирования

1. Установление полного перечня работ,
которые необходимо выполнить при
планировании комплекса работ.

2. Составление топологии сети — четкой
последовательности и взаимосвязей всех
работ и построение сетевого графика.

3. Оценка продолжительности выполнения
отдельных работ.

4. Расчет параметров сетевого графика.

5. Анализ и оптимизация сетевого графика.

6. Управление ходом работ по сетевому
графику.

2. Параметры сетевой модели

В
системах СПУ применяются различные
типы сетевых моделей, отличающиеся
составом информации о комплексе работ.

Встречаются
модели с детерминированной и вероятностной
структурой сети, с детерминированными
и вероятностными оценками продолжительности
работ сети. При выборе модели руководителю
проекта приходится принимать компромиссное
решение: с одной стороны, сетевая модель
должна быть простой, а с другой –
адекватной объекту.

Широкое
применение получила сетевая модель ПДВ
(простейшая детерминированная временная),
которая характеризуется следующими
тремя моментами:

а)
имеется сеть с единственным исходным
и единственным завершающим событием;

б)
продолжительности всех работ t_ijизвестны, однозначно определены
(вспомните из математики: детерминант
– определитель) и указаны на графике
(обычно в днях, в зарубежной практике –
чаще в неделях);

в)
задан момент начала выполнения комплекса
Т₀,а также задается (но не обязательно)
директивный срокТ_дир
наступления завершающего события.

Рассмотрим
временные параметры этой модели.

По
известным продолжительностям работ
легко определить продолжительность
каждого пути – t(L).Продолжительность любого пути равна
сумме продолжительностей работ, его
составляющих:

(1)

Для
пояснения обратимся к рис.1. На графике
над стрелками указаны продолжительности
работ в днях (напомним, что продолжительность
фиктивной работы равна нулю).

Рис. 1

Найдем
на графике полные пути и определим их
продолжительность (по номерам событий):

L₁
1 – 2 – 5 – 7 – 8 t(L₁)
= 14 дн.

L₂
1 – 2 – 4 – 5 – 7 – 8 t(L₂)
= 12 дн.

L₃
1 – 3 – 4 – 5 – 7 – 8 t(L₃)
= 13 дн.

L₄
1 – 3 – 6 – 7 – 8 t(L₄)
= 16 дн.

Всегда найдется путь, имеющий наибольшую
продолжительность, он называется
критическим–L_кр.
Его продолжительность получила особое
обозначение:

t(L_кр)=Т_кр .

Понятие критического пути является
центральным понятием в системе СПУ.
Значение L_кр, во-первых, состоит в том, что он является
самым длинным путем в сети и, таким
образом, является единственным путем,
который определяет полную продолжительность
процесса. Поэтому, если мы хотимопределитьполную продолжительность процесса,
нужно определитьТ_кр, а определять для этой цели все остальныеt(L)
не имеет смысла. Во-вторых, если мы
хотимсократитьпродолжительность
процесса, нужно прежде всего сокращать
продолжительность работ, принадлежащихL_кр. Таким образом, логика сетевого
планирования приводит нас к необходимости
находить в сетях критические пути и
определять их продолжительность.

На графике рис. 1 путь L₄имеет наибольшую продолжительность,
равную 16 дням, и потому является
критическим. Обычно критический путь
на графиках выделяется (цветными,
двойными, жирными и т.п. стрелками).

Обратим
внимание, что в сети может быть несколько
критических путей (с точки зрения
использования ресурсов – чем больше
критических путей в графике, тем лучше).

Обычно
к L_кр
принадлежит 10-15 % работ. Чем сложнее
сеть, тем таких работ меньше (считается,
что в сети средней сложности количество
работ в 1,7 раза превышает количество
событий).

Другие
полные пути рассматриваемого сетевого
графика могут либо полностью проходить
вне критического пути (L₁иL₂),
либо частично с ним совпадать (L₃).
Эти пути называютсяненапряженными:
на участках, не совпадающих с критической
последовательностью работ, они имеют
резервы времени. Задержка в наступлении
событий, лежащих на этих участках, до
определенного момента не влияет на срок
завершения всего комплекса.

Из
ненапряженных путей наибольшее внимание
привлекают наименее напряженные и
подкритические. Подкритические путиимеют продолжительность, близкую кТ_кр(отличаются отТ_крна определенную величину, устанавливаемую
руководителем проекта). Эти пути могут
стать критическими в результате задержки
выполнения их работ или в результате
сокращения продолжительности работ,
лежащих на критическом пути, и,
следовательно, являются потенциально
опасными с точки зрения соблюдения
сроков завершения проекта.

Например,
при увеличении времени выполнения
работы 2-5 (рис. 1) на 2 дня это приведет
к тому, что t(L₁)
= 16 дн. =Т_кр.
ТогдаL₁тоже
станет критическим и будет определять
срок выполнения всего комплекса.

Наименее
напряженные пути могут рассматриваться
с точки зрения возможности использования
ресурсов (рабочей силы, оборудования,
денежных средств). Возможное удлинение
этих путей, вызванное переброской
ресурсов, до определенных пределов не
опасно для сроков проекта.

Работы,
принадлежащие критическому и подкритическим
путям, составляют критическую зонукомплекса (15-20 % всех работ).

Зная
продолжительность всех работ, можно
также определить сроки наступления
всех событий сети. Для каждого события
определяют ранний и поздний сроки его
наступления.

Ранний
срок наступления события– это минимальный из возможных моментов
его наступления, когда будут выполнены
все работы, предшествующие данному
событию. Он определяется максимальной
из продолжительностей всех путей,
предшествующих данному событию:

(2)

где
— путь, предшествующий данному событиюi;

— максимальный из этих путей.

Поясним
это на примере рис. 1. Событию 5 предшествуют
три пути: 1-2-5 с продолжительностью 7 дн.,
1-2-4-5 с продолжительностью 5 дн. и 1-3-4-5 с
продолжительностью 6 дн. Событие 5 не
может наступить ранее 7 дней, т.к. только
в течение этого периода будут выполнены
все предшествующие ему работы 2-4, 3-4 и
2-5.

Легко
увидеть, что для события 3 ранний
срок его наступления
= 4 дн., т.к. ему предшествует только один
путь 1-2, состоящий из одной работы.

Поздний
срок наступления события— это максимальный из допустимых моментов
его наступления, при котором еще не
изменяется общий срок выполнения всего
комплекса. Поздний срок определяется
разностью междуТ_кри наибольшей из продолжительностей
путей, следующих за событиемi:

(3)

где
— путь, следующий за событиемi;

— максимальный из этих путей.

Продолжим
рассмотрение рис. 1. За событием 5 следует
только один путь 5-7-8 продолжительностью
7 дней. Следовательно,

= 16 – 7 = 9 дн.

За
событием 3 следуют два пути: 3-4-5-7-8 с
продолжительностью 9 дн. и 3-6-7-8 с
продолжительностью 12 дн. Следовательно,
= 16 – 12 = 4 дн., т.е. событие 3 не может
наступить позже 4 дней от начала работ,
иначе это скажется на изменении срока
всего комплекса.

Так
как по определению критического пути

, (4)

то для всех
событий, принадлежащих критическому
пути, справедливо равенство:

(5)

В
справедливости этого мы уже убедились
из рассмотренного примера для события
3. Оно лежит на критическом пути, поэтому

== 4 дн.

Зная
сроки наступления событий, можно для
каждой работы сети определить сроки ее
начала и окончания, выявив тем самым
возможности смещения сроков. Применительно
к каждой работе рассматриваются четыре
срока:

• ранний срок начала работы ;
  (6)

• ранний срок окончания работы ;
  (7)

• поздний срок начала работы ;
  (8)

• поздний срок окончания работы .
  (9)

С
учетом равенства (5) для событий, лежащих
на критическом пути, можно сделать
вывод, что у работ критического пути
ранние и поздние сроки начала или
окончания совпадают:

₍₁₀₎

Следующим
важным параметром является резерв
времени – применительно к пути, событию
и работе.

Критический
путь является самым продолжительным в
сети. Разность между продолжительностью
критического пути Т_кри продолжительностью любого другого
путиt(L)называется резервом времени путиLи обозначается:

(11)

Чем
короче путь L,
чем больше он по времени не совпадает
с критическим, тем у него больше резерв
времени. Физический смысл этого параметра
таков:резерв времени пути
показывает, на сколько в сумме могут
быть увеличены продолжительности работ,
принадлежащих путиL,
чтобы при этом не изменился общий срок
выполнения всего комплекса работ.

Так,
L₁(см. рис. 1) не совпадает с критическим
на участке сети между 1 и 7 событиями.
Его продолжительность, как было показано
выше, составляет 14 дней, и, следовательно,
резерв равен двум дням. Только двумя
днями располагают руководители всех
трех работ при непредвиденной задержке
в их выполнении.

Все
события, не лежащие на критическом пути,
обладают резервом времени, который
определяется как разность между поздним
и ранним сроками его наступления:

.
(12)

Резерв
времени события
показывает, на какой предельно
допустимый срок можно задержать
наступление этого события, не вызывая
при этом увеличения срока выполнения
всего комплекса работ. При большей
задержке критический путь переместится
на максимальный из путей, проходящих
через данное событиеi.

Так,
для события 5 (рис.1)

= 9 – 7 = 2 дн. При задержке этого события
на 2 и более дней критический путь
переместится на максимальный путьL₁
, проходящий через событие 5.

События,
лежащие на критическом пути, имеют
нулевой резерв времени, в том числе
исходное и завершающее события.

Для
работ сетевой модели определяются два
резерва времени: полный и свободный.

Полный
резерв времени работы
— это резерв максимального из путей,
проходящих через работуi,j

,
(13)

где
— поздний срок наступления конечного
события этой работы;

— ранний срок наступления начального
события этой работы;

— продолжительность выполнения работы.

Физический
смысл этого параметра таков: этот резерв
показывает, на сколько можно задержать
начало или увеличить продолжительность
отдельной работы, не изменяя директивного
(или раннего, если директивный не задан)
срока наступления завершающего события.
В последнем случае (если директивный
срок не задан) – не изменяя Т_кр.

Обратим
внимание на следующий важный момент:
полный резерв принадлежит не одной
работе, а всем путям, которые проходят
через данную работу. Поэтому использование
его полностью на одной из работ пути L
аннулирует полные резервы временивсех работ, принадлежащих этому
пути.

Например,

= 2дн. (см. рис.1), т.к. он определяется
резервом путиL₁.
Если использовать его полностью на
работе 5-7, то другие работы этого пути
(1-2, 2-5) останутся без резервов времени.

Полные
резервы времени принимают минимальное
значение у работ, лежащих на критическом
пути. Это свойство является необходимым
и достаточным условием принадлежности
работы критическому пути и используется
для его нахождения при расчете сети.
Минимальное значение полного резерва
равно нулю, если Т_дирне задан или превышает момент начала
работТ₀на величинуТ_кр
. В общем случае оно равно
разности (Т_кр
— Т_дир).

Свободный
резерв времени работыпредставляет собой максимальное время,
на которое можно задержать начало или
увеличить продолжительность работыi,j
при условии, что все события сети
наступают в свои ранние сроки:

.
(14)

Свободный
резерв образуется не у всех работ, а
только у работ, непосредственно
принадлежащих событиям, через которые
проходят пути с различной продолжительностью.
Это надо понимать так: если событию
предшествует одна работа (например,
работа 1-2 на рис.1), то для нее свободный
резерв равен нулю по определению (=
0), в других случаях –0.

Свободный
резерв является частью полного, и потому
чаще на практике применяется другая
формула:

,
(15)

где
– резерв конечного события работыi,j.

Свободный
резерв показывает, какая часть полного
резерва времени работы может быть
использована для увеличения ее
продолжительности при условии, что это
не вызовет изменения раннего сроканаступления ее конечного события.
Свободный резерв является независимым
резервом, т.е. использование его на одной
из работ не изменяет величины свободных
резервов времени остальных работ сети.
Используя свободный резерв времени,
ответственный исполнитель может
маневрировать в его пределах временем
начала данной работы, ее окончания или
ее продолжительностью, не затрагивая
интересов других руководителей работ.

Соседние файлы в папке ОиПП1

• #
• #
• #
• #
• #

Ниже приведенная информация является справочным материалом. Подробнее о данном материале и его практическом применении вы можете узнать, просмотрев видео.

Содержание:

1. Описание критического пути.
2. Даты и резервы работ.
3. Методы оценки длительности проекта.
4. Сокращение критического пути.

Описание критического пути

Критический путь – это последовательность задач (или даже одна задача), изменения длительности, которой изменит длительность проекта. 

Задачам, которые лежат на критическом пути, а также ресурсам, назначенным на эти задачи, необходимо уделять особое внимание, если своевременное завершение проекта является критическим фактором успеха проекта. Именно эти элементы определяют возможность своевременного завершения проекта.
В большинстве случаев последовательности задач взаимосвязаны зависимостями между задачами. Хотя в проекте может быть несколько подобных сетей задач, критическим путем проекта будет являться только сеть, которая заканчивается последней.
По мере выполнения проекта роль критического пути могут играть разные последовательности задач. Это зависит от степени завершенности критических задач (задач, лежащих на критическом пути), а также от задержек в выполнении других последовательностях задач. (В проекте всегда выделяется один основной критический путь. Новые критические пути, как правило, являются ветвлениями этого основного пути). Проект завершается только после завершения последней задачи из критического пути.

Критической называется задача, задержки в выполнении которой, оттягивают дату завершения проекта. В типичном проекте многие задачи имеют некоторый резерв времени и поэтому их выполнение может быть задержано без влияния на дату завершения проекта. Временной резерв для задачи – это объем времени, в течение которого задержка выполнения задачи не приведет к задержке выполнения других задач или проекта в целом.

По мере того, как Вы модифицируете задачи для того, чтобы разрешить перераспределение ресурсов, выровнять затраты или изменить содержание проекта, будьте внимательны по отношению к критическим задачам, поскольку их изменение повлечет изменение даты завершения проекта. Критические задачи составляют критический путь проекта.
Задача становится критической, если она удовлетворяет одному из следующих условий:

• Она имеет нулевой временной резерв.
• На нее наложено ограничение «Фиксированное начало» или «Фиксированное окончание».
• Дата завершения задачи совпадает с крайним сроком.

Задача перестает быть критической, если она помечается, как завершенная, поскольку она уже больше не может влиять на срок завершения последующей задачи или проекта в целом.

Даты и резервы работ

Временной резерв определяется датами раннего и позднего завершения задачи. Дата раннего завершения задачи – это самый ранний срок, в который может быть окончена задача в соответствии с датой начала выполнения и длительностью задачи. Дата позднего завершения задачи – это самый поздний срок, в который может быть завершена задача без влияния на дату завершения проекта. Разница между датами раннего и позднего завершения составляет временной резерв задачи.  Для критических задач (т.е. для тех задач, которые не имеют временного резерва) дата раннего завершения совпадает с датой позднего завершения задачи.

Метод критического путь  позволяет построить основной путь проекта и выделить ключевые работы проекта. Отсутствие или некачественное планирование связей между работами делает метод критического пути неэффективным.
Метод критического пути эффективен при некачественном планировании или отсутствие параллельных работ проекта.Критические работы не имеют резервов. Работы, не лежащие на критическом пути, имеют: свободные резервы и общий резерв. Для работ, лежащих на критическом пути, даты начала совпадают с датами раннего начала и позднего начала, а окончание совпадает с датами раннего окончания и позднего окончания.

Методы оценки длительности проекта

Сокращение критического пути

Если Вы хотите уменьшить дату завершения проекта, Вам необходимо уменьшить даты завершения всех задач, лежащих на критическом пути. Для этого Вам необходимо произвести следующее:

1. Уменьшите длительность или суммарную работу задачи;
2. Измените ограничение, наложенное на задачу, на другое ограничение, более гибкое. Вполне возможно, что при изменении ограничения MS Project сможет назначить выполнение задачи на более ранний срок;
3. Разбейте критическую задачу на мелкие подзадачи, которые могут выполняться одновременно разными ресурсами;
4. Пересмотрите зависимости межу задачами для обеспечения более гибкого расчета графика;
5. Установите интервал опережения между зависимыми задачами там, где это возможно;
6. Попытайтесь запланировать использование нерабочего времени ресурсов;
7. Назначьте дополнительные ресурсы на задачи, которые лежат на критическом пути.

Помните, что если Вы сократите сроки завершения задач, лежащих на критическом пути, на основе другой последовательности задач может возникнуть новый критический путь.

Данный материал рассматривается на практических тренингах на ресурсе Онлайн-курсы.

Цели

В данной главе показаны возможности использования метода СРМ (Critical Path Method — метод критического пути) для конт­роля сроков выполнения проекта. Таким проектом может быть разработка нового продукта или производственного процесса, строительство предприятия, здания или сооружения, ремонт слож­ного оборудования и т. д.

При реализации проекта составляется график выполнения ра­бот. Для того чтобы проект был завершен вовремя, необходимо контролировать сроки выполнения этих работ. Усложняющим фактором является то, что работы взаимосвязаны. Одни работы зависят от выполнения других и не могут начаться, пока предшест­вующие работы не будут завершены.

Важной предпосылкой применения метода СРМ является пред­положение о том, что время выполнения каждой работы точно известно.

В результате использования метода СРМ удается получить от­веты на следующие вопросы:

1. За какое минимальное время можно выполнить проект?

2. В какое время должны начаться и закончиться отдельные работы?

3. Какие работы являются «критическими» и должны быть вы­полнены точно в установленное время, чтобы не был сорван срок выполнения проекта?

4. На какое время можно отложить срок выполнения «некри­тической» работы, чтобы она не повлияла на срок выполне­ния проекта в целом?

После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь определять и использовать для экономи­ческого анализа:

• наиболее раннее и наиболее позднее время начала работы;

• наиболее раннее и наиболее позднее время окончания работы;

• критический путь;

• длину критического пути;

• запас времени на выполнение работы.

Модели

Исходным шагом для применения метода СРМ является опи­сание проекта в виде перечня выполняемых работ с указанием их взаимосвязи. Для описания проекта используются два основных способа: Табличный и Графический.

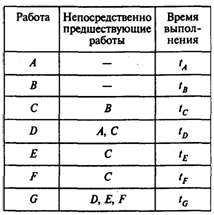
Рассмотрим следующую таблицу, описывающую проект:

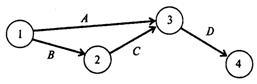
В первом столбце указаны наименования всех работ проекта. Их четыре: А, В, С, D. Во втором столбце указаны работы, непо­средственно предшествующие данной. У работ А и В нет предшест­вующих. Работе С непосредственно предшествует работа В. Это означает, что работа С может быть начата только после того, как завершится работа В. Работе D непосредственно предшествуют две работы: А и С. Это означает, что работа D может быть начата толь­ко после того, как завершатся работы А и С. В третьем столбце таблицы для каждой работы указано время ее выполнения. На основе этой таблицы может быть построено графическое описа­ние проекта (рис. 1).

Рис. 1

На рис. 1 проект представлен в виде графа с вершинами 1,2, 3, 4 и дугами А, В, С, D. Каждая вершина графа отображает собы­тие. Событие 1 означает начало выполнения проекта. Иногда та­кое событие обозначают буквой S (Start). Событие 4 означает за­вершение проекта. Для обозначения такого события иногда ис­пользуют Букву F( Finish). Любая работа проекта — это упорядочен­ная пара двух событии. Например, работа А есть упорядоченная пара событий (1, 3)(см. рис. 1). Работа D — упорядоченная пара событий (3,4). Событие проекта состоит в том, что завершены все работы, «входящие» в соответствующую вершину. Например, со­бытие 3 состоит в том, что завершены работы А и С.

Рассмотрим другой проект, представленный следующей табли­цей:

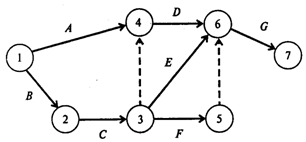
Графическое описание проекта, построенное по этой таблице, имеет вид, показанный на рис. 2.

Рис.2

В этом графическом описании проекта, кроме тех работ, ко­торые указаны в таблице, использованы две «фиктивные» работы (3, 4) и (5, 6). На рисунке они показаны штриховыми линиями. Эти работы не требуют времени на их выполнение и используют­ся в графическом представлении проекта лишь для того, чтобы правильно отобразить взаимосвязь между работами. Получив гра­фическое представление проекта, мы обеспечили себе возмож­ность провести расчеты методом СРМ.

Определения:

Путь — последовательность взаимосвязанных работ, ведущая из одной вершины проекта в другую вершину. Например, {A, D, G} и {В, С, Е, С} — два различных пути, ведущие из вершины 1 в вер­шину 7 (см. рис. 2).

Длина пути — суммарная продолжительность выполнения всех работ пути.

Критический путь — путь, суммарная продолжительность вы­полнения всех работ которого является наибольшей.

Ясно, что минимальное время, необходимое для выполнения любого проекта, равно длине критического пути. Именно на ра­боты, принадлежащие критическому пути, следует обращать осо­бое внимание. Если такая работа будет отложена на некоторое время, то и срок окончания проекта будет отложен на то же вре­мя. Если необходимо сократить время выполнения проекта, то в первую очередь нужно сократить время выполнения хотя бы од­ной работы на критическом пути.

Для того чтобы найти критический путь, достаточно перебрать все пути и выбрать тот или те из них, что имеют наибольшую сум­марную продолжительность выполнения работ. Однако для боль­ших проектов реализация такого подхода связана с вычислитель­ными трудностями. Метод СРМ позволяет получить критический путь намного проще.

Пусть I И J — вершины, или события, проекта, (I,J) — работа проекта, S — событие «начало проекта» (Start), F — событие «окон­чание проекта» (Finish), Т — длина критического пути.

Введем следующие обозначения:

T(I,J) — время выполнения работы (I, J);

ES(I,J) —наиболее раннее время начала работы (I,J);

EF(I,J) —наиболее раннее время окончания работы (I,J);

LS(I,J) —наиболее позднее время начала работы (I,J),

LF(I,J) — наиболее позднее время окончания работы (I,J),

Ei — наиболее раннее время наступления события I;

Li — наиболее позднее время наступления события I;

R(I,J) — полный резерв времени на выполнение работы (I,J) (время, на которое может быть отложена работа (I,J) Без увеличения продолжительности выполнения все­го проекта);

R(I,J) — свободный резерв времени на выполнение работы (I,J) (время, на которое может быть отложена работа (I,J) Без увеличения наиболее раннего времени ЕI наступ­ления последующего события J).

Если (I,J) — работа проекта, то имеют место соотношения:

Для любого J ES(I,J) = ЕI;

Для любого I LF(I,J) = Lj.

Для того чтобы использовать метод СРМ для нахождения критического пути, необходимо для каждой работы (I,J) опреде­лить наиболее раннее время начала и окончания работы (ES(i, j) и EF(I,J)) и наиболее позднее время начала и окончания работы (LS(I,J) и LF(I,J)).

Метод СРМ описывается следующими соотношениями:

(1)

Для любой работы (S,J), выходящей из стартовой вершины S про­екта;

(2)

Т. е. наиболее раннее время окончания любой работы (I,J) превы­шает наиболее раннее время начала этой работы (время наступ­ления предшествующего события I) на время ее выполнения;

(3)

Т. е. наиболее раннее время начала работы (Q, J) равно наиболь­шему из значений наиболее раннего времени окончания непо­средственно предшествующих ей работ;

(4)

Т. е. длина критического пути равна наиболее раннему времени завершения проекта;

(5)

Т. е. наиболее позднее время окончания любой работы, заверша­ющей проект, равно длине критического пути;

(6)

Т. е. наиболее позднее время начала любой работы меньше наибо­лее позднего времени окончания этой работы (времени наступле­ния последующего события) на время ее выполнения;

(7)

Т. е. наиболее позднее время окончания работы (/, Q) равно наи­меньшему из значений наиболее позднего времени начала непо­средственно следующих за ней работ;

(8)

Т. е. полный резерв времени на выполнение любой работы равен разности между наиболее поздним и наиболее ранним временем ее начала или разности между наиболее поздним и наиболее ран­ним временем ее окончания;

(9)

Т. е. свободный резерв времени на выполнение любой работы ра­вен разности между наиболее поздним временем наступления последующего события и наиболее ранним временем окончания работы.

Из приведенных выше определений и соотношений непосред­ственно вытекают следующие утверждения:

1. Длина критического пути равна Т.

2. Если R(I,J) = 0, то работа (I,J) лежит на критическом пути;

Если R(I, j) > 0, то работа (I,J) не лежит на критическом пути.

3. Если время начала работы (I,J), не лежащей на критичес­ком пути, отложить на срок меньший, чем R(I,J), то наиболее ран­нее время наступления последующего события не изменится.

4. Если время начала работы (I,J), не лежащей на критичес­ком пути, отложить на срок меньший, чем R(i, j), то время, необ­ходимое на выполнение всего проекта, не увеличится.

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.