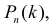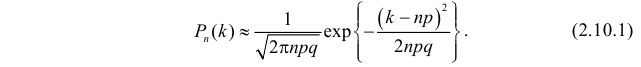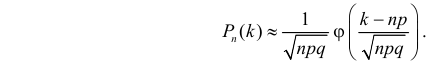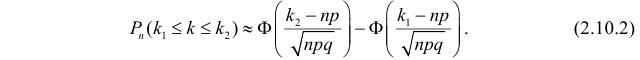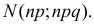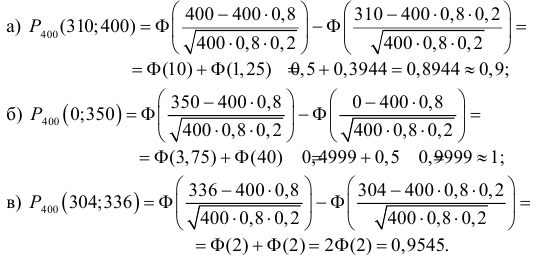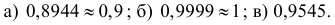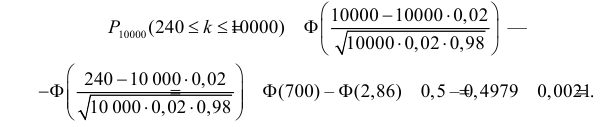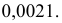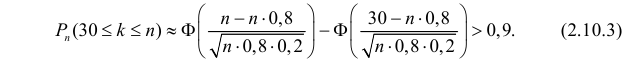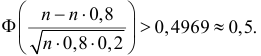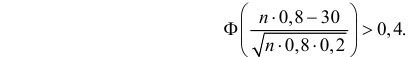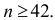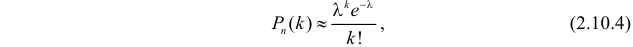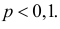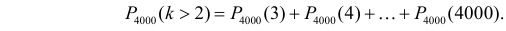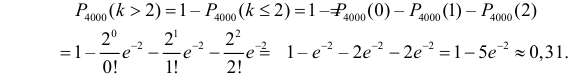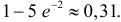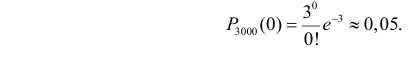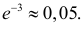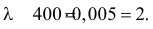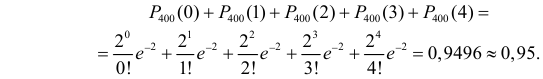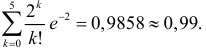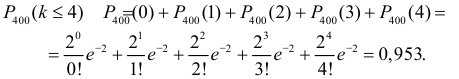В страховой компании застраховано 10000 автомобилей вероятность поломки

Локальная и интегральная теоремы Муавра–Лапласа:

При большом числе опытов n формула Бернулли (2.6.1) приводит к большому объему вычислений. Существуют приближенные формулы для вычисления вероятностей

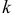
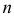
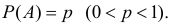
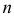
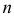
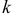
Пусть – число появлений события A в независимых опытах, в каждом из которых Тогда при достаточно больших (хотя бы несколько десятков) вероятность того, что в независимых опытах событие A ровно раз, определяется формулой

Эта формула составляет содержание локальной теоремы Муавра– Лапласа. Для вычисления вероятностей по формуле (2.10.1) удобно пользоваться таблицей функции 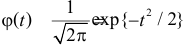(см. прил., табл. П1). Использование этой функции позволяет записать искомую вероятность в виде 

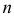
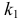
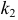
Вероятность того, что в независимых опытах событие A появится от до раз, определяется формулой 

Эта формула составляет содержание интегральной теоремы Муавра–Лапласа.

Замечание. Правая часть формулы (2.10.1) соответствует функции плотности вероятности нормального закона распределения Формула (2.10.2) является формулой (2.9.2), записанной для нормального закона распределения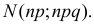

Пример:

Восемьдесят процентов приборов после сборки нуждаются в регулировке. Какова вероятность того, что среди 400 собранных за смену приборов в регулировке нуждаются: а) не менее 310; б) не более 350; в) от 304 до 336?

Решение. Сборку каждого прибора можно считать независимым испытанием с вероятностью появления события равной 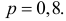 Так как число опытов велико, то можно воспользоваться интегральной теоремой Муавра–Лапласа (2.10.2):

Ответ. 

Пример:

В страховой компании застраховано 10000 автомобилей. Вероятность поломки любого автомобиля в результате дорожно-транспортного происшествия равна 0,02. Каждый владелец застрахованного автомобиля платит в год 24 у.е. страховых и в случае поломки автомобиля в результате аварии получает от компании 1000 у.е. Найдите вероятность того, что по истечении года работы компания потерпит убытки от этого вида страховой деятельности.

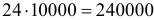
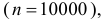
Решение. Страховой сбор с 10000 владельцев автомобилей составляет у.е. Компания потерпит убытки, если будет предъявлено более 240 исков по 1000 у.е. каждый. Вероятность поступления страхового иска от каждого автовладельца равна 0,02. Эксплуатацию каждого автомобиля в течение страхового срока можно считать независимым испытанием. Так как число испытаний велико то можно воспользоваться интегральной теоремой Муавра- Лапласа. По формуле (2.10.2)

Ответ. 

Пример:

Вероятность попадания в цель при выстреле равна 0,8. Сколько нужно запланировать выстрелов, чтобы с вероятностью большей 0,9 можно было получить не менее 30 попаданий.

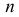
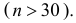
Решение. Каждый выстрел считаем независимым опытом. Из условий задачи легко видеть, что число выстрелов должно быть достаточно большим Поэтому можно воспользоваться интегральной формулой Муавра–Лапласа (2.10.2):

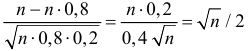
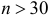
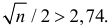
Заметим, что  и при  величина  Поэтому 

В итоге неравенство (2.10.3) можно переписать в виде 

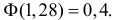
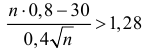
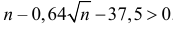
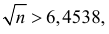
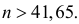
По таблице функции Лапласа находим, что  Так как функция Лапласа строго возрастает, то или  Откуда т.е. Итак,

Ответ. 42.

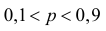
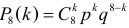
Замечание. При значениях формула Муавра–Лапласа (2.10.2) дает приближение приемлемой точности, так как многоугольник распределения при большом числе опытов напоминает по форме функцию плотности вероятности нормального закона распределения (см. рис. 2.10.1, на котором указаны вероятности при разных значениях ). 

Формула Пуассона

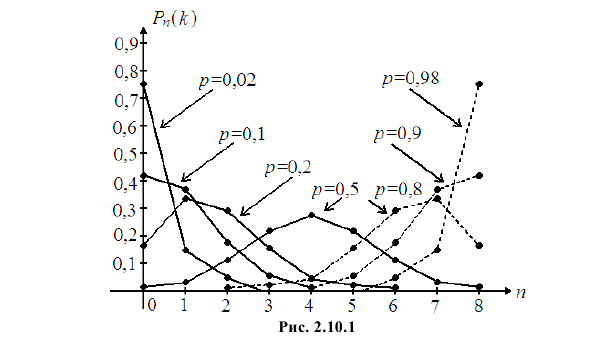
При значениях вероятности появления события близких к нулю или единице многоугольник распределения существенно несимметричен (см. рис. 2.10.1). Приближенная формула (2.10.1) не обеспечивает приемлемой точности. В этих условиях для вычисления вероятностей 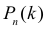используют обычно формулу Пуассона (2.10.4).

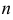
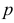
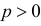
Пусть число независимых опытов велико (чем больше, тем лучше), а вероятность события мала (чем меньше, тем лучше, но ). Тогда

где 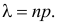 Эту формулу называют формулой Пуассона. Формула Пуассона дает приемлемую точность, если производится хотя бы несколько десятков опытов, а

Пример:

Вероятность того, что изделие при транспортировке с завода повредится, равна 0,0005. С завода отправлено четыре тысячи изделий. Какова вероятность того, что в пути повредится больше двух изделий?

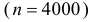
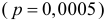
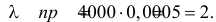
Решение. Транспортировку каждого изделия можно рассматривать как независимый опыт, число которых велико. Вероятность же появления события в каждом опыте мала. Это дает основание воспользоваться для вычислений формулой Пуассона (2.7.1). Заметим, что Нас интересует вероятность

Проще эту вероятность вычислить, если рассмотреть вероятность противоположного события:

Ответ. 

Пример:

Известно, что из каждой 1000 элементов в среднем 999 сохраняют свою работоспособность в течение гарантийного срока. Какова вероятность того, что из 3000 элементов все до единого сохранят свою работоспособность в течение гарантийного срока?

Решение. Работу каждого элемента в течение гарантийного срока можно считать независимым опытом. Число опытов велико (n = 3000 ). Вероятность того, что элемент сохранит работоспособность в течение гарантийного срока, равна 0,999. Формула Бернулли (2.6.1) из-за большого числа опытов для расчетов неприемлема. Для применения формулы Пуассона будем говорить не о работоспособных элементах, а об элементах вышедших из строя. 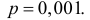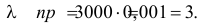Вероятность выхода из строя элементам  Тогда Все 3000 элементов сохранят свою работоспособность, если ни один из них не выйдет из строя. По формуле Пуассона (2.7.1) 

Ответ. 

Пример:

В студенческом строительном отряде работает 400 студентов. Вероятность того, что студент в течение всего срока работы получит травму, требующую введения противостолбнячной сыворотки, равна 0,005. Какое минимальное количество доз сыворотки должно быть в медсанпункте этого отряда, чтобы с вероятностью не менее 0,95 их хватило в случае необходимости?

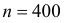
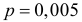
Решение. Работу каждого студента в строительном отряде можно считать независимым опытом. Имеем большое число опытов, а вероятность травмы – мала. Поэтому можно воспользоваться формулой Пуассона (2.7.1), в которой

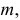
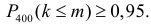
Минимальное количество доз можно найти как минимальное при котором выполняется неравенство Непосредственный подсчет по формуле (2.7.1) показывает, что

Заметим, что добавление к четырем еще одной дозы дает

Ответ. 4.

Пример:

Предстоит произвести профилактический осмотр 400 устройств. Вероятность того, что в осматриваемом устройстве некоторый элемент потребуется заменить, равна 0,005. Какова вероятность того, что придется заменить не более четырех элементов?

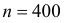
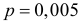
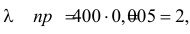
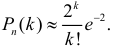
Решение. Осмотр каждого устройства можно считать независимым опытом, и всего таких опытов планируется . Вероятность замены детали – мала. Поэтому формула Муавра–Лапласа неприемлема. В этих условиях лучше воспользоваться асимптотической формулой Пуассона. Так как  то  Поэтому 

Ответ. 0,953.

Для вычисления вероятностей по формуле (2.10.1) удобно1пользоваться таблицей функции j(t )exp{= -t 2 / 2} (см. прил., табл.2pП1). Использование этой функции позволяет записать искомуювероятность в видеæ k — np ö1Pn (k ) »j çç÷.npq è npq ÷ø93Вероятность того, что в n независимых опытах событие A появитсяот k1 до k2 раз, определяется формулойæ k — np öæ k1 — np öPn (k1 £ k £ k2 ) » F çç 2F(2.10.2)÷÷çç÷÷ .npqnpqèøèøЭта формула составляет содержание интегральной теоремыМуавра–Лапласа.Замечание.

Правая часть формулы (2.10.1) соответствует функцииплотности вероятности нормального закона распределения N (np; npq ).Формула (2.10.2) является формулой (2.9.2), записанной для нормальногозакона распределения N (np; npq ).Пример 2.52. Восемьдесят процентов приборов после сборкинуждаются в регулировке. Какова вероятность того, что среди 400собранных за смену приборов в регулировке нуждаются: а) не менее 310; б)не более 350; в) от 304 до 336?Решение. Сборку каждого прибора можно считать независимымиспытанием с вероятностью появления события равной р = 0,8.

Так какчисло опытов велико, то можно воспользоваться интегральной теоремойМуавра–Лапласа (2.10.2):æ 400 — 400 × 0,8 öæ 310 — 400 × 0,8 × 0, 2 öа) Р400 (310;400) = F ç÷ — Fç÷=4000,80,24000,80,2××××èøèø= F (10) + F (1, 25) =0,5 + 0,3944 = 0,8944 » 0,9;æ 350 — 400 × 0,8 öæ 0 — 400 × 0,8 öб) Р400 ( 0;350 ) = F ç÷ — Fç÷=400×0,8×0,2400×0,8×0,2èøèø= F(3,75) + F (40) 0,=4999 + 0,5 0,9999=» 1;æ 336 — 400 × 0,8 öæ 304 — 400 × 0,8 × 0,2 öв) Р400 ( 304;336 ) = F çF÷ç÷=400×0,8×0,2400×0,8×0,2èøèø= F(2) + F (2) = 2F(2) = 0,9545.Ответ.

а) 0,8944 » 0,9 ; б) 0,9999 » 1 ; в) 0,9545.Задача 2.52.1. Вероятность того, что передаче по каналу связисигнал из-за помех будет искажен, равна p. Оцените вероятность того, чтопри независимой передаче n сигналов: а) от k1 до k2 из них будут искажены;б) не менее k1 из них будут искажены; в) не более k2 из них будутискажены. (См. пример 2.52 и исходные данные.)Исходные данные к задаче 2.52.1.nnn k1 k2№ pk1 k2 № pk1 k2 № p94123456789100,02 500 5 120,02 400 6 200,02 600 9 140,02 700 10 160.02 800 12 200,02 900 14 200,02 1000 15 220,01 1000 8 140,03 500 10 150,03 600 14 16111213141516171819200,030,030,010,010,010,010,010,010,010,0170080080090010001500200012004001600161866812148101224261213142022141618212223242526272829300,010,020,020,020,010,030,020,010,020,01500 10 16500 8 12400 6 15600 8 12900 7 10400 8 13400 7 12700 4 10200 39300 38Задача 2.52.2.

Известно, что p процентов жителей нашего городаподдерживают некоторое мероприятие. Какова вероятность того, что приопросе наугад n жителей не менее k из них выскажутся в поддержкумероприятия. (См. пример 2.52 и исходные данные.)Исходные данные к задаче 2.52.2.pnkpnkpnk№№№1520025 11 1040035 21 701006513520065 12 2015035 22 50200 11022015025 13 2020045 23 502009532520055 14 60200 115 24 352007543010025 15 5015070 25 203005554010045 16 60200 125 26 203006562520045 17 5015080 27 203007071520035 18 50300 140 28 253008084510050 19 5020090 29 2540090910045 20 50200 105 30 25400 10510 50Пример 2.53.

В страховой компании застраховано 10000автомобилей. Вероятность поломки любого автомобиля в результатедорожно-транспортного происшествия равна 0,02. Каждый владелецзастрахованного автомобиля платит в год 24 у.е. страховых и в случаеполомки автомобиля в результате аварии получает от компании 1000 у.е.Найдите вероятность того, что по истечении года работы компанияпотерпит убытки от этого вида страховой деятельности.Решение. Страховой сбор с 10000 владельцев автомобилейсоставляет 24 × 10000= 240000 у.е.

Компания потерпит убытки, если будетпредъявлено более 240 исков по 1000 у.е. каждый. Вероятностьпоступления страхового иска от каждого автовладельца равна 0,02.Эксплуатацию каждого автомобиля в течение страхового срока можносчитать независимым испытанием. Так как число испытаний велико95( n = 10000 ), то можно воспользоваться интегральной теоремой МуавраЛапласа. По формуле (2.10.2)æ 10000 — 10000 × 0,02 ö=FçР10000 (240 £ k £ 10000)÷ ––10000×0,02×0,98èøæ 240 — 10 000 × 0,02 ö-F ç=F(700) – F(2,86) 0,5 –=0,4979 0,0021.=ç 10 000 × 0,02 × 0,98 ÷÷èøОтвет.

0,0021.Задача 2.53. Медицинская страховка туриста стоит 300 рублей. Принаступлении страхового случая (травма, заболевание и т.д.) туристполучает страховку m тыс. рублей. Страховая компания застраховала nтуристов. Вероятность наступления страхового случая для каждого туристаравна p.

Какова вероятность того, что страховая компания потерпит убыткиот этого вида страховой деятельности?Какова вероятность того, что доход компании от этого видастраховой деятельности превысит 10k тыс. рублей в вариантах 1–15, ипревысит 5k в вариантах 16–30, где k –– номер варианта? (См. пример 2.53и исходные данные.)Исходные данные к задаче 2.53.mnpmnpmnp№№№20 2000 0,01 11 2000 0,025 4121 20 4000 0,01520 3000 0,015 12 3000 0,014222 25 4000 0,02525 2000 0,02 13 4000 0,015 2323 20 5000 0,01525 3000 0,025 14 4000 0,021424 25 5000 0,01520 4000 0,01 15 5000 0,025 4525 20 2000 0,02525 4000 0,015 16 5000 0,014626 20 3000 0,025420 5000 0,02 17 2000 0,0227 25 2000 0,01725 5000 0,025 18 3000 0,015828 25 3000 0,0220 2000 0,015 19 2000 0,025929 20 4000 0,02520 3000 0,02 20 3000 0,015 530 25 4000 0,0110Пример 2.54.

Вероятность попадания в цель при выстреле равна 0,8.Сколько нужно запланировать выстрелов, чтобы с вероятностью большей0,9 можно было получить не менее 30 попаданий.Решение. Каждый выстрел считаем независимым опытом. Изусловий задачи легко видеть, что число выстрелов n должно бытьдостаточно большим ( n > 30 ). Поэтому можно воспользоватьсяинтегральной формулой Муавра–Лапласа (2.10.2):96æ n — n × 0,8 öæ 30 — n × 0,8 ö(2.10.3)Pn (30 £ k £ n) » F ç÷ — Fç÷ > 0,9.××××nn0,80,20,80,2èøèøn — n × 0,8n × 0,2Заметим, что== n / 2 и при n > 30 величинаn × 0,8 × 0,2 0, 4 næ n — n × 0,8 ön / 2 > 2,74.

Поэтому F ç÷ > 0,4969 » 0,5.××n0,80,2èøВ итоге неравенство (2.10.3) можно переписать в видеæ n × 0,8 — 30 öFç÷ > 0, 4.××n0,80,2èøПо таблице функции Лапласа находим, что F(1, 28) = 0,4. Так какn × 0,8 — 30функция Лапласа строго возрастает, то> 1,28 или0,4 nn – 0,64 n — 37,5 > 0. ОткудаОтвет. 42.n > 6,4538, т.е. n > 41,65. Итак, n ³ 42.Задача 2.54. При разливе выплавленного металла вероятностьполучить годную отливку равна p. Сколько нужно запланировать отливок,чтобы с вероятностью больше P после проверки получить не менее kгодных отливок? (См. пример 2.54 и исходные данные.)Исходные данные к задаче 2.54.Pk № pPk № pPk № pPk№ p1 0,9 0,9 25 9 0,6 0,9 40 17 0,8 0,8 50 25 0,5 0,9 352 0,9 0,95 40 10 0,9 0,9 35 18 0,5 0,9 30 26 0,6 0,9 303 0,6 0,9 35 11 0,7 0,9 35 19 0,8 0,9 45 27 0,9 0,95 254 0,9 0,9 30 12 0,6 0,8 40 20 0,6 0,9 45 28 0,6 0,95 355 0,7 0,9 30 13 0,9 0,95 35 21 0,7 0,9 40 29 0,8 0,9 406 0,6 0,8 30 14 0,6 0,9 25 22 0,5 0,9 40 30 0,9 0,95 307 0,8 0,9 35 15 0,5 0,9 45 23 0,9 0,95 50 31 0,8 0,9 358 0,5 0,9 25 16 0,9 0,9 40 24 0,8 0,9 30 32 0,6 0,8 40Замечание.

При значениях 0,1 < p < 0,9 формула Муавра–Лапласа(2.10.2) дает приближение приемлемой точности, так как многоугольникраспределения при большом числе опытов напоминает по форме функциюплотности вероятности нормального закона распределения (см. рис. 2.10.1,на котором указаны вероятности P8 (k ) = C8k p k q 8-k при разных значениях p).97Рис. 2.10.12.10.2.

Формула ПуассонаПри значениях вероятности появления события близких к нулю илиединице многоугольник распределения существенно несимметричен (см.рис. 2.10.1). Приближенная формула (2.10.1) не обеспечивает приемлемойточности. В этих условиях для вычисления вероятностей Pn (k ) используютобычно формулу Пуассона (2.10.4).Пусть число независимых опытов n велико (чем больше, тем лучше),а вероятность события p мала (чем меньше, тем лучше, но p > 0 ).

Тогдаl k e -l,(2.10.4)k!где l = nр. Эту формулу называют формулой Пуассона. Формула Пуассонадает приемлемую точность, если производится хотя бы несколько десятковопытов, а p < 0,1.Pn (k ) »Пример 2.55. Вероятность того, что изделие при транспортировке сзавода повредится, равна 0,0005. С завода отправлено четыре тысячиизделий. Какова вероятность того, что в пути повредится больше двухизделий?Решение. Транспортировку каждого изделия можно рассматриватькак независимый опыт, число которых ( n = 4000 ) велико. Вероятность жепоявления события в каждом опыте ( p = 0,0005 ) мала. Это дает основаниевоспользоваться для вычислений формулой Пуассона (2.7.1). Заметим, чтоl np 4000=× 0,0005= = 2.

Нас интересует вероятность98P4000 (k > 2) = P4000 (3) + P4000 (4) + K + P4000 (4000).Проще эту вероятность вычислить, если рассмотреть вероятностьпротивоположного события:P4000 (k > 2) = 1 – P4000 ( k £ 2) = 1 – =P4000 (0) – P4000 (1) – P4000 (2)20 -2 21 -2 22 -2= 1 – e — e — e = 1 – е -2 – 2е -2 — 2е -2 = 1 — 5е -2 » 0,31.0!1!2!-2Ответ. 1 — 5 е » 0,31.Задача 2.55. При дальней радиосвязи из-за помех каждый сигналнезависимо от других с вероятностью p может быть принят ошибочно.Передано n сигналов.

Какова вероятность того, что k из них будут принятыошибочно? Какова вероятность ошибочного приема не менее k сигналов?(См. пример 2.55 и исходные данные.)Исходные данные к задаче 2.55.№pnk№pnk№pnk1 0,01 2001 11 0,004 2503 21 0,0025 40032 0,01 2002 12 0,004 2502 22 0,005 40013 0,01 2003 13 0,008 2501 23 0,005 40024 0,015 2001 14 0,008 2502 24 0,005 40035 0,015 2002 15 0,008 2503 25 0,005 60026 0,015 2003 16 0,01 3002 26 0,005 60037 0,02 2002 17 0,01 3003 27 0,005 60048 0,02 2003 18 0,01 3004 28 0,0025 80019 0,02 2004 19 0,0025 4001 29 0,0025 800210 0,004 2501 20 0,0025 4002 30 0,0025 8003Пример 2.56.

Известно, что из каждой 1000 элементов в среднем 999сохраняют свою работоспособность в течение гарантийного срока. Каковавероятность того, что из 3000 элементов все до единого сохранят своюработоспособность в течение гарантийного срока?Решение. Работу каждого элемента в течение гарантийного срокаможно считать независимым опытом. Число опытов велико ( n = 3000 ).Вероятность того, что элемент сохранит работоспособность в течениегарантийного срока, равна 0,999. Формула Бернулли (2.6.1) из-за большогочисла опытов для расчетов неприемлема. Для применения формулыПуассона будем говорить не о работоспособных элементах, а об элементахвышедших из строя.