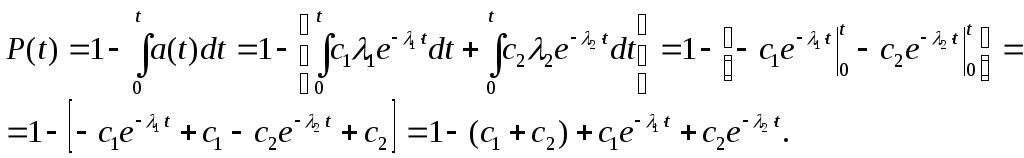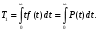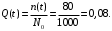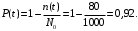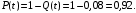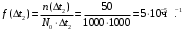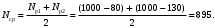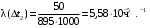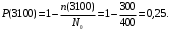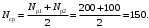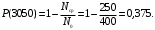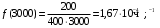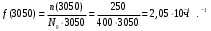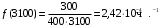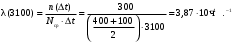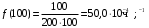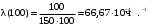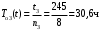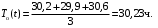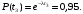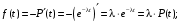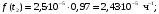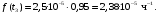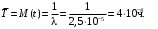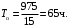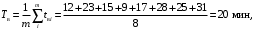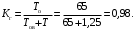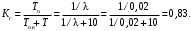В течение некоторого периода времени производилось наблюдение за работой программного обеспечения

Задача
1. В
течение некоторого периода времени
производилось наблюдение за работой
одного экземпляра радиолокационной
станции. За весь период наблюдения было
зарегистрировано
15 отказов.
До начала наблюдения станция проработала
258 час,
к концу наблюдения наработка станции
составила
К час.
Требуется определить среднюю наработку
на отказ t_cp.

К=1233+№
варианта

Решение

1.Наработка
радиолокационной станции за наблюдаемый
период равна:

t=t₂-t₃=1233-258=975
час.

2. Принимая
час, по формуле,
находим среднюю наработку на отказ:

час

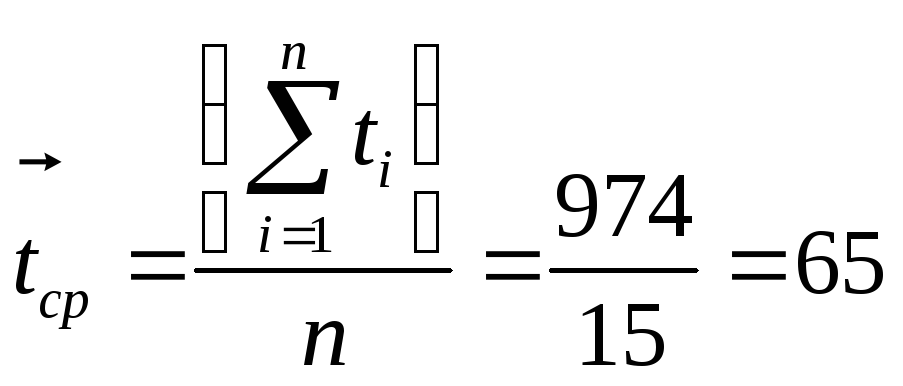
Задача
2.
Производилось наблюдение за работой
трех экземпляров однотипной аппаратуры.
За период наблюдения было зафиксировано
по первому экземпляру аппаратуры
6 отказов,
по второму и третьему—11
и 8
отказов соответственно. Наработка
первого экземпляра составила
К₁
час,
второго—
К₂
и третьего—
К₃
час. Требуется
определить наработку аппаратуры на
отказ.

К₁=181+№
варианта

К₂=329+№
варианта

К₃=245+№
варианта

Решение

1.Определяем
суммарная наработку трех образцов
аппаратуры:

час.

2.Определяем
суммарное количество отказов:

отказов.

3.Находим среднюю
наработку на отказ по формуле

час

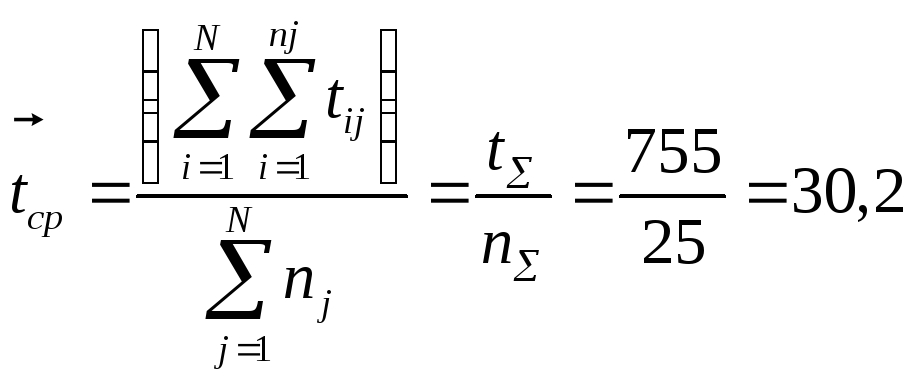
Задача
3. Система
состоит из
5 приборов,
причем отказ любого одного из них ведет
к отказу системы. Известно, что первый
прибор отказал
34 раза в
течение К₁
час.
работы, второй—24
раза в течение
К₂
час.
работы, а остальные приборы в течение
К₃
час.
работы отказали
4, 6 и
5 раз
соответственно. Требуется определить
наработку на отказ системы в целом, если
справедлив экспоненциальный закон
надежности для каждого из пяти приборов.

К₁=952+№
варианта

К₂=960+№
варианта

К₃=210+№
варианта

Решение

Для решения этой
задачи воспользуемся следующими
соотношениями:

и

1.Определим
интенсивность отказов для каждого
прибора:

2. Интенсивность
отказов системы будет

3. Средняя наработка
отказа системы равна:

Задача
4. За
наблюдаемый период эксплуатации в
аппаратуре было зафиксировано
8 отказов.
Время восстановления составило: t₁=(12+№
варианта)
мин;
t₂=(23+№
варианта)
мин;
t₃=(15+№
варианта)
мин;
t₄=(9+№
варианта)
мин;
t₅=(17+№
варианта)
мин;
t₆=(28+№
варианта)
мин;
t₇=(25+№
варианта)
мин; t₈=(31+№
варианта)
мин.

Требуется определить
среднее время восстановления аппаратуры.

Решение

мин.

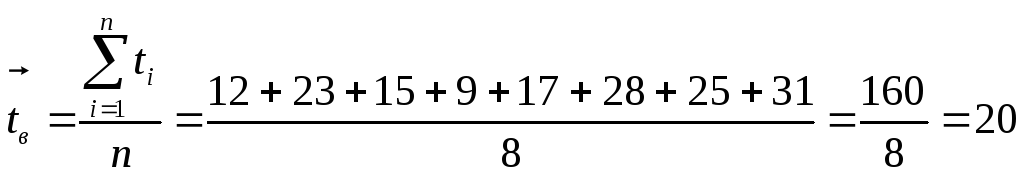
Задача
5. Пусть
время работы элемента до отказа подчинено
экспоненциальному закону распределения
с параметром =2,5*
10^-5
1/час.

Требуется вычислить
количественные характеристики надежности
элемента P(t),
a(t),
T_cp,
если
t=(500+№
варианта),
(1000+№
варианта),
(2000+№
варианта)
час.

Таблица
1

Основные соотношения для количественных характеристик надёжности при различных законах распределения времени до отказа

Решение

Используем формулы
для P(t),
a(t)
и T_ср,
приведенные в табл. 2

1. вычислим вероятность
   безотказной работы:

Используя данные
таблицы 3, получим:

1. Вычислим частоту
   отказа:

3. Вычислим среднюю
наработку до первого отказа:

Задача
6. Допустим,
что в результате анализа данных об
отказах аппаратуры частота отказов
получена в виде

Требуется определить
все количественные характеристики
надежности и построить графические
зависимости.

Решение

1.Определим
вероятность безотказной работы. На
основании формулы имеем

имеем

Вычислим сумму
c₁+c₂.
Так как

Тогда

2.найдем зависимость
интенсивности отказов от времени по
формуле
:

1. Определим среднюю
   наработку до первого отказа. На основании
   формулы
   

1. Вычислим зависимость
   параметра потока отказов от времени.
   Воспользуемся формулой
   ,,
   для чего найдем преобразование Лапласа
   частоты отказовa(t):

Подставляя
полученное значение в формулу
,.

Находим

Задача
7. Известно,
что интенсивность отказов
=(0,02+10^-3№варианта)
1/час, а
среднее время восстановления t_в
=10 час.
Требуется вычислить функцию и коэффициент
готовности изделия.

Решение

В нашем случае
средняя наработка до первого отказа
час.

Тогда коэффициент
готовности будет

Функцию готовности
легко вычислить по формуле

Задача
8. Время
безотказной работы гироскопического
устройства с шарикоподшипниками в осях
ротора гироскопа подчиняется закону
Вейбулла с параметрами
k=1,5 ₀=10^-4
1/час,
а время его работы t=(100+№
варианта)
чаc.
Требуется
вычислить количественные характеристики
надежности такого устройства.

Решение

Определим вероятность
безотказной работы по формуле

Подставляя значения
,t
и k
из условий задачи, получим

Частота отказов
определяется по формуле

Тогда

Вычислим среднюю
наработку до первого отказа по формуле

В начале вычислим
значение гамма-функции. В нашем случае
x=(1/k)+1=(1/1,5)+1=1,67
тогда T(x)=0,9033.
Подставляя в выражения для T_ср
значения
гамма-функции и параметры распределения
иk
получим

Задача
9. Пусть
время работы до отказа подчинено
нормальному усеченному закону
распределения с параметрами
и
=1000,
2000, 3000, 4000
час. Требуется
вычислить количественные характеристики
надежности P(t),
a(t),
(t),
Т_cр
для
t=4000, 6000, 8000. 10000
час.

Решение

Используя формулы
таблицы 1. сведем найденные данные в
таблицу 2

Соседние файлы в папке Nad_rgz

• #
• #

Стандартизация, сертификация и управление качеством программного обеспечения Экзамен

1 2 3 4 5 6

При определении качества программных средств оперируют тремя группами показателей, которые характеризуют:

Некоторые ответы приведены ниже. Для гарантированной сдачи тестов можете заказать у нас полное прохождение тестов.

Заказать прохождение тестов

• |
• Библиотека задач
• |
• В течение некоторого периода времени производилось наблюдение за работой одного прибора. За весь период

С этим файлом связано 2 файл(ов). Среди них: ПМ.04.docx, kos_pm_02 (1).docx.
Показать все связанные файлы

Подборка по базе: Практические задания налоги.docx, Право 9 задания.docx, ОРВ задания.docx, 1 класс задания.docx, Организация инновационной деятельности — практические задания.do, Психология управления — практические задания.docx, Управление человескими ресурсами — практические задания.docx, Тест с ответами Версия 13.1 от 17.11.2021. Временные методически, Тест с ответами по теме Методические рекомендации COVID-19 Верс, Разбор задания.docx

Практическая работа №2.
Показатели надежности объекта

Цель: приобретение навыков расчета показателей надежности невосстанавливаемого объекта.

Задачи:

• повторить основные теоретические сведения;
• ознакомиться с примерами решения задач, решить задачи.

Основные теоретические сведения

Рассмотрим временной интервал работы t [0…τ]:

• при t=0 элемент начинает работать;
• при t=τ происходит его отказ.

Время τ имеет случайный характер, поэтому в качестве основных функций, определяющих надежность элемента можно принять:

• функцию распределения отказа

(1)

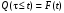
• функцию надежности

(2)

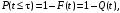
Вероятность отказа

Вероятность отказа – это вероятность того, что в пределах заданной наработки или заданном интервале времени произойдет отказ объекта:

• вероятностное определение (1):

(3)

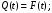
• статистическое определение:

. (4)

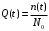
где n(t) – число отказавших к моменту времени t изделий;

N₀ – число изделий, поставленных на испытания.

Вероятность безотказной работы

Вероятность безотказной работы – это вероятность того, что в пределах заданной наработки или заданном интервале времени отказ объекта не возникает:

• вероятностное определение (2):

(5)

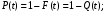
• статистическое определение:

(6)

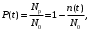
где N_р –число работоспособных к моменту времени t изделий;

N₀ – число изделий, поставленных на испытания.

Частота отказов (плотность распределения отказов)

• вероятностное определение:

(7)

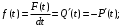
• статистическое определение:

(8)

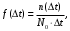
где n(Δt) – число отказавших объектов в интервале Δt.

Интенсивность отказов

Интенсивность отказов – это условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не наступил:

• вероятностное определение:

(9)

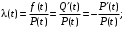
• статистическое определение:

. (10)

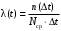
гдеn(Δt) – число отказов однотипных объектов на интервале Δt, для которого определяется интенсивность отказов;

N_ср – среднее число исправно работающих объектов в интервале Δt

(11)

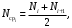
N_i, N_i+1 –число исправно работающих объектов в начале и конце интервала Δt.

Общее выражение для вероятности безотказной работы

(12)

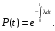
Пояснение. Прологарифмируем формулу (10):

.

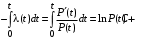
Величина постоянной С определяется из условия, что t=0:

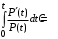
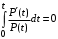
P(0)=1 и ln1=0; ; ; С=0.

Средняя наработка до отказа

Средняя наработка до отказа – математическое ожидание наработки объекта до первого отказа.

Вероятностное определение:

Статистическое определение

(13)

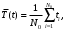
где N₀ – число работоспособных однотипных невосстанавливаемых объектов при t = 0 (в начале испытания);

t_i – наработка до отказа i-го объекта.

Средняя наработка на отказ

(14)

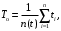
где t_i – наработка между i-1 и i-м отказами, ч;

n(t) – суммарное число отказов за время t.

Среднее время восстановления

(15)

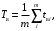
m– число отказов последствия которых устранены;

t_вi – время восстановления работоспособного состояния после i-го отказа.
Коэффициент готовности

Вероятность того, что изделие будет работоспособно в произвольный момент времени, кроме периодов, когда применение изделия по назначению исключено

(16)

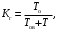
где T_о− средняя наработка на отказ;

T_в− среднее время восстановления.

Коэффициент технического использования

Характеризует долю времени нахождения элемента в работоспособном состоянии относительно рассматриваемой продолжительности эксплуатации

(17)

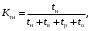
где t_н− суммарная наработка изделия в рассматриваемый промежуток времени;

t_в, t_pи t_о− суммарное время, затраченное на восстановление, ремонт и ТО изделия за тот же период.

Примеры решения задач

Пример 1. На испытание поставлено N₀=1000 однотипных электронных ламп. За 3000 ч отказало n(t)=80 ламп. Требуется определитьза период 3000 ч вероятность отказаQ(t) и вероятность безотказной работы P(t).

Решение

Вероятность отказа (4):

Вероятность безотказной работы (6)

либо

Пример 2. На испытание поставлено N₀=1000 однотипных электронных ламп. За первые Δt₁=3000 ч отказало 80 ламп, а за интервал времени Δt₂=3000…4000 чотказало еще Δt₂=50 ламп. Требуется определить частотуf(Δt₂) и интенсивностьλ(Δt₂) отказов электронных ламп в промежутке времени ∆t = 3000–4000 ч.

Решение

Частота отказов (7)

Интенсивность отказов (10)

.

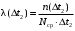
Среднее число исправно работающих объектов в интервале (11)

Пример 3. На испытание поставлено N₀=400 изделий. За время t=3000 ч отказало n(3000)=200 изделий, за последующий интервал ∆t=100 ч отказало n(∆t)=100 изделий. Требуется определить вероятность безотказной работы P(t), частоту отказовf(t) и интенсивность отказовλ(t) за 3000, 3100, 3050 часов, частоту интенсивность λ(t) отказов в интервале 3000…3100 часов.

Решение

Вероятность безотказной работы (6):

;

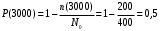
Среднее время исправно работающих изделий в интервале ∆t=100 ч:

Число изделий, отказавших за время t=3050 ч:

n(3050)=N₀–N_ср=400–150=250.

тогда

Частота отказа за 3000, 3100, 3050 часов (начало интервалов t=0):

Интенсивность отказов за 3000, 3100, 3050 часов (начало интервалов t=0):

;

;

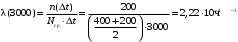
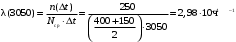
В интервале ∆t= 100 ч (начало интервала t=3000):

Пример 4. Три однотипных объекта поставлены на испытания. За период наблюдения было зафиксировано по первому объекту 6 отказов, по второму – 11, третьему – 8. Наработка первого объекта составила t₁=181 ч, второго t₂=329 ч, третьего t₃=245 ч. Определить наработку объектов на отказ.

Решение

, ,

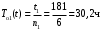
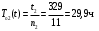
Пример 5. Пусть время работы элемента до отказа подчинено экспоненциальному закону λ=2,5·10^–5 ч^–1 (λ=const). Требуется определить вероятность безотказной работы P(t), частоту отказов f(t) и среднюю наработку до отказа T при t=500, 1000, 2000 ч.

Решение

Выражение (12) при λ=cоnst примет вид

.

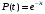
Тогда:

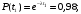
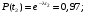
Частота отказов (7):

Тогда:

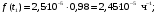
Т.к. средняя наработка на отказ – это математическое ожидание случайной наработки объекта до первого отказа, а математическое ожидание при экспоненциальном законе распределения

,

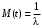
то

Пример 6. В течение некоторого периода времени производилось наблюдение за работой одного объекта. За весь период зарегистрированоn(t)=15 отказов. До начала наблюдений объект проработал 258 ч, к концу наблюдения наработка составила 1233 ч. Определить среднюю наработку на отказ T_o.

Решение

Наработка за указанный период составила

∆t=t₁–t₂=1233–258=975 ч.

Приняв 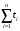= 975 ч, определим среднюю наработку на отказ по статистическим данным (14)

Пример 7. В аппаратуре было зафиксировано 8 отказов. Время восстановления составило: t₁ = 12 мин, t₂ = 23 мин, t₃ = 15 мин, t₄= 9 мин, t₅= 17 мин, t₆ = 28 мин, t₇ = 25 мин, t₈ = 31 мин.

Требуется определить среднее время восстановления аппаратуры t_в.

Решение

Среднее время восстановления аппаратуры (2.14)

Пример 8. Аппаратура имела среднюю наработку на отказ Т_о=65 ч и среднее время восстановления Т_в=1,25 ч. Требуется определить коэффициент готовности К_г.

Решение

Коэффициент готовности (16)

Пример 9. Известно, что интенсивность отказов λ= 0,02 ч^–1, а среднее время восстановления t_в=10 ч. Требуется вычислить коэффициент готовности и функцию готовности изделия. Закон распределения экспоненциальный.

Решение

Коэффициент готовности (16)

Пример 10. Определить коэффициент технического использования машины, если известно, что машину эксплуатируют в течение года Т_э=8760 ч. За этот период эксплуатации машины суммарное время восстановления отказов составило t_в=40 ч. Время проведения регламента составляет t_о=20 ч. Суммарное время, затраченное на ремонтные работы за период эксплуатации составляет 15 суток (t_р =15·24=360 ч).

Решение

Определим суммарное время наработки машины:

t_н=Т_э – (t_в+t_р+t_о)=8760 – (40+360+20)=8340.

Определим коэффициент технического использования (17)

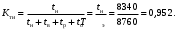
Задачи для решения

Задача 1. На испытание поставлено N₀=1500 однотипных электронных ламп. За 5000 ч отказало n(t)=100 ламп. Требуется определитьза период 3000 ч вероятность безотказной работы P(t)и вероятность отказаQ(t).

Задача 2. На испытание поставлено N₀=2000 однотипных приборов. За первые Δt₁=3000 ч отказало 100 приборов, а за интервал времени Δt₂=3000…4000 чотказало еще Δt₂=100 приборов. Требуется определить частотуf(Δt₂) и интенсивностьλ(Δt₂) отказов приборов в промежутке времени ∆t = 3000–4000 ч.

Задача 3. На испытание поставлено N₀=500 изделий. За время t=3000 ч отказало n(3000)=100 изделий, за интервал ∆t=100 ч отказало n(∆t)=50 изделий. Требуется определить вероятность безотказной работы P(t), частоту отказовf(t) и интенсивность отказовλ(t) за 3000, 3100, 3050 часов, частоту интенсивность λ(t) отказов в интервале 3000…3100 часов.

Задача 4. Три однотипных объекта поставлены на испытания. За период наблюдения было зафиксировано по первому объекту 8 отказов, по второму – 10, третьему – 8. Наработка первого объекта составила t₁=160 ч, второго t₂=300 ч, третьего t₃=240 ч. Определить наработку объектов на отказ.

Задача 5. Пусть время работы элемента до отказа подчинено экспоненциальному закону λ=2,5·10^–5 ч^–1. Требуется определить вероятность безотказной работы P(t), частоту отказов f(t) и среднюю наработку до отказа 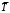при t=1000, 2000, 3000 ч.

Задача 6. В течение некоторого периода времени производилось наблюдение за работой одного объекта. За весь период зарегистрированоn(t)=10 отказов. До начала наблюдений объект проработал 258 ч, к концу наблюдения наработка составила 1000 ч. Определить среднюю наработку на отказ T_o

Задача 7. В аппаратуре было зафиксировано 10 отказов. Время восстановления составило: t₁=10 мин, t₂=20 мин, t₃=12 мин, t₄=10 мин, t₅=15 мин, t₆=25 мин, t₇=25 мин, t₈=30 мин.

Требуется определить среднее время восстановления аппаратуры t_в.

Задача 8. Аппаратура имела среднюю наработку на отказ Т_о=75 ч и среднее время восстановления t_в=1,2 ч. Требуется определить коэффициент готовности К_г.

Задача 9. Известно, что интенсивность отказов λ= 0,01 ч^–1, а среднее время восстановления t_в=5 ч. Требуется вычислить коэффициент готовности. Закон распределения экспоненциальный.

Задача 10. Определить коэффициент технического использования машины, если известно, что машину эксплуатируют в течение года Т_э=9010 ч. За этот период эксплуатации машины суммарное время восстановления отказов составило t_в=50 ч. Время проведения регламента составляет t_о=10 ч. Суммарное времяt_р, затраченное на ремонтные работы за период эксплуатации составляет 10 суток.