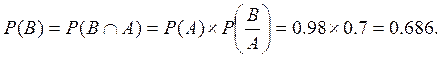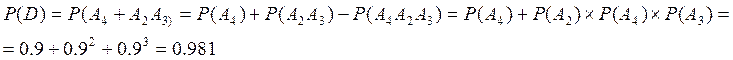Условие
96. Вероятности того, что во время работы цифровой электронной машины произойдет сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах, относятся как 3:2:5. Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.
математика ВУЗ
21287
Решение
★
Задача на применение формулы полной вероятности.
Вводим в рассмотрение гипотезы:
H_(1) -»сбой в арифметическом устройстве»
Н_(2) — »сбой в оперативной памяти»
Н_(3) — » сбой в остальных устройствах»
р(H_(1))+p(H_(2))+p(H_(3))=1
По условию
р(H_(1)):p(H_(2)):p(H_(3))=3:2:5
Пусть
р(H_(1))=3k,
p(H_(2))=2k,
p(H_(3))=5k
3k+2k+5k=1
k=0,1
Значит
р(H_(1))=0,3,
p(H_(2))=0,2,
p(H_(3))=0,5
Событие А — »возникший в машине сбой будет обнаружен»
р(А/H_(1))=0,8
р(А/H_(1))=0,9
р(А/H_(1))=0,9
р(А)=р(А/H_(1))*p(H_(1))+р(А/H_(2))*p(H_(2))+р(А/H_(3))*p(H_(3))=
=0,8*0,3+0,9*0,2+0,9*0,5=0,24+0,18+0,45=0,87
О т в е т. 0,87
Написать комментарий
1.Два
датчика посылают сигналы в общий канал
связи, причем первый из них посылает
вдвое больше сигналов, чем второй.
Вероятность получить искаженный сигнал
от первого датчика равна 0,06; от второго
– 0,03.
а) Какова
вероятность получить искаженный сигнал
в общем канале связи?
б) В общем
канале связи получен искаженный сигнал.
Какова вероятность того, что этот сигнал
послан вторым датчиком?
2.
Вероятности того, что во время работы
цифровой электронной машины произойдет
сбой в арифметическом устройстве, в
оперативной памяти, в остальных
устройствах, относятся как 3:2:5. Вероятности
обнаружения сбоя в арифметическом
устройстве, в оперативной памяти и в
остальных устройствах соответственно
равны 0,8; 0,9; 0,9. Найти вероятность того,
что возникший в машине сбой будет
обнаружен.
H1 –»сбой
в арифметическом устройстве»
Н2 –
»сбой в оперативной памяти»
Н3 –
» сбой в остальных
устройствах»
р(H1)+p(H2)+p(H3)=1
По
условию
р(H1):p(H2):p(H3)=3:2:5
Пусть
р(H1)=3k,
p(H2)=2k,
p(H3)=5k
3k+2k+5k=1
k=0,1
Значит
р(H1)=0,3,
p(H2)=0,2,
p(H3)=0,5
Событие
А – »возникший в машине сбой будет
обнаружен»
р(А/H1)=0,8
р(А/H1)=0,9
р(А/H1)=0,9
р(А)=р(А/H1)·p(H1)+р(А/H2)·p(H2)+р(А/H3)·p(H3)=
=0,8·0,3+0,9·0,2+0,9·0,5=0,24+0,18+0,45=0,87
О т
в е т. 0,87
3.
А — событие,
состоящее в том, что вынутый шар будет
белым.
Когда из I в II перекладывали
шары, возможны три случая:
1) пусть
H1 — это событие, состоящее в том, что оба
шара белые:
P(H1)=P(б*б)
=2/5*1/4=2/20=1/10
P(A|H1)=3/7
2) пусть H2 — это
событие, состоящее в том, что один белый,
один черный:
P(H2)=P(б*ч)
=2/5*3/4=6/20=3/10
P(A|H2)=2/7
3) пусть H3 — это
событие, состоящее в том, что оба шара
черные:
P(H3)=P(ч*ч)
=3/5*2/4=6/20=3/10
P(A|H3)=1/7
Теперь по формуле
полной
вероятности:
P(A)=P(H1)*P(A|H1)+P(H2)*P(A|H2)+P(H3)*P(A|H3)
P(A) = 1/10*3/7+
3/10*2/7 + 3/10*1/7 = 0,17
4. Радист
трижды вызывает корреспондента.
Вероятность того, что будет принят
первый вызов, равна 0,2, второй – 0,3, третий
– 0,4. События, состоящие в том, что данный
вызов будет услышан, независимы. Найти
вероятность того, что корреспондент
услышит вызов радиста.
Вероятность
того, что корреспондент не услышит
радиста при первом вызове 1-0,2 = 0,8, при
втором 1-0,3 = 0,7 — и третьим 1-0,4 = 0,6
Поскольку
события независимы, то вероятность
равна 0,8*0,7*0,6 = 0,336
А вероятность
того, что корреспондент услышит радиста
хотя бы один раз равна 1 -0,336 = 0,664
5. В лифт
семиэтажного дома на первом этаже вошли
три человека. Каждый из них с одинаковой
вероятностью выходит на любом из этажей,
начиная со второго. Найти вероятности
следующих событий: А — все пассажиры
выйдут на четвертом этаже; В — все
пассажиры выйдут одновременно (на одном
и том же этаже); С— все пассажиры выйдут
на разных этажах.
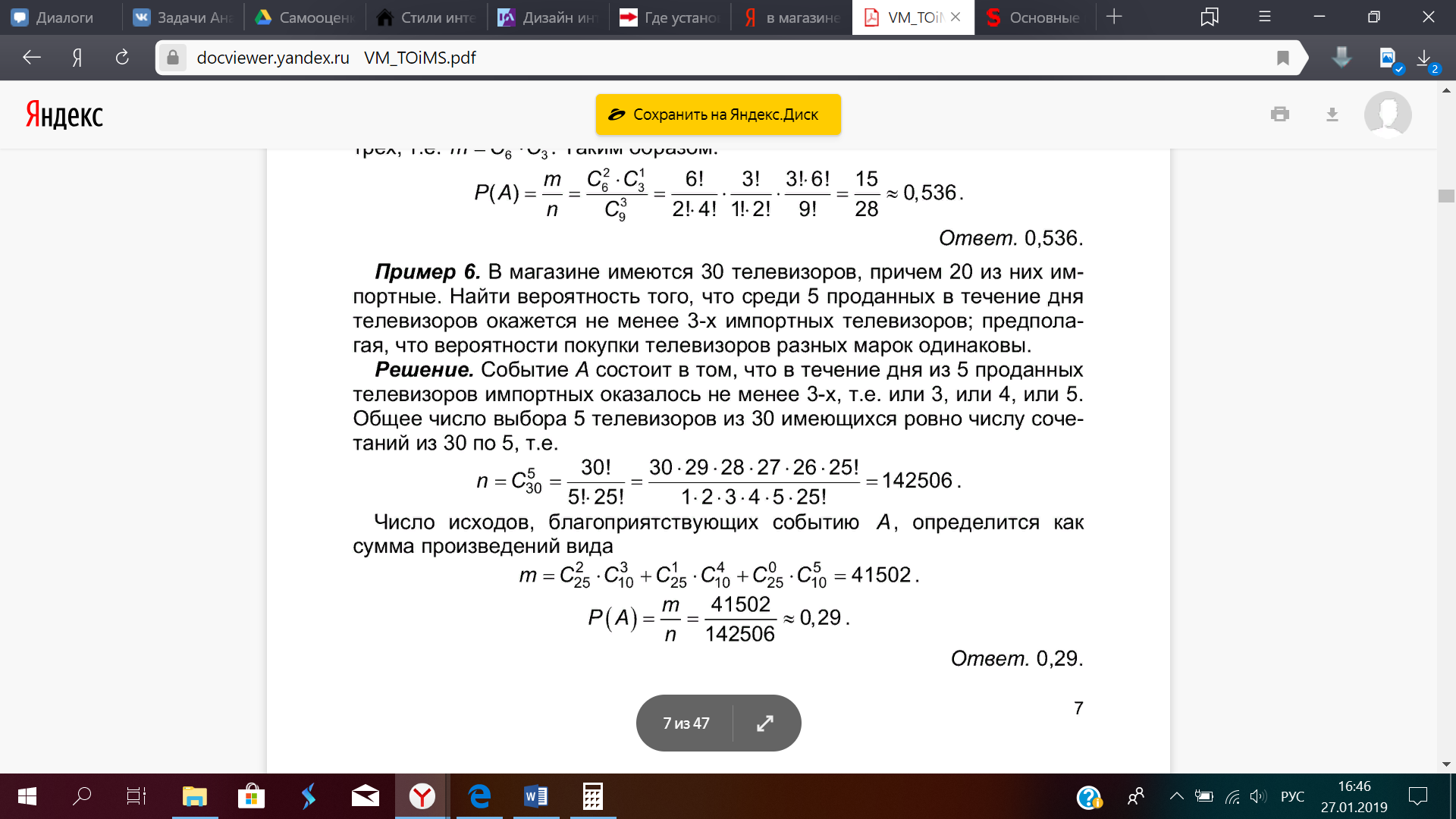
6. В
магазине имеются 30 телевизоров, причем
20 из них импортных. Найти вероятность
того, что среди 5 проданных в течение
дня телевизоров окажется не менее 3
импортных телевизоров, предполагая,
что вероятности покупки телевизоров
разных марок одинаковы.
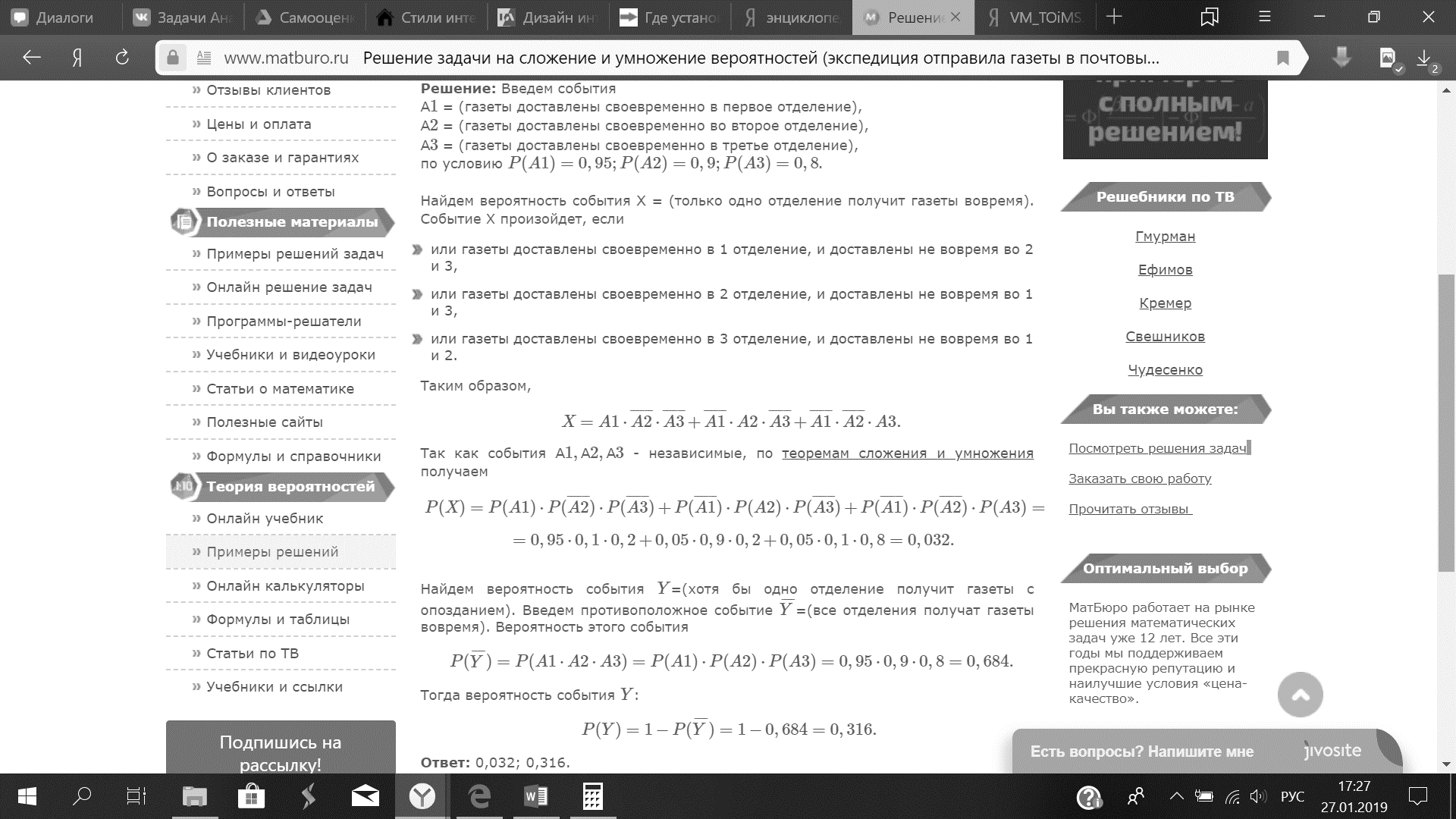
9.
Экспедиция издательства отправила
газеты в три почтовых отделения.
Вероятность своевременной доставки
газет в первое отделение равна 0,95, во
второе — 0,9, в третье — 0,8. Найти вероятность
следующих событий:
а) только одно
отделение получит газеты вовремя;
б)
хотя бы одно отделение получит газеты
с опозданием.
4.В
блок входят три радиолампы. Вероятности
выхода из
строя
в течение гарантийного срока для них
соответственно равны 0,3;0,2 и 0,4. Какова
вероятность того, что в течение
гарантийного срока хотя бы одна радиолампа
выйдет из строя?
Решение.
Обозначим
через Ai событие, состоящее в том, что i
–ая радиолампа выйдет из строя ( i =
1,2,3) . Известно, чтоP (A1) = 0,3 , P (A2 ) = 0,2 , P (A3
) = 0,4 .
Событие
B = A1 + A2 + A3 означает, что хотя бы одна
радиолампа в течение гарантийного срока
выйдет из строя. События A1, A2 , A3 совместны.
Введем противоположное событие B/ − ни
одна из трех радиоламп не выходит из
строя: B/ = A1/ ⋅
A2/ ⋅
A3/ . События
Ai /и Ai независимы друг от друга, поэтому
P
(B/)
= P
(A1/)
⋅P
(A2/
) ⋅P
(A3
/) = (1−P
(A1))(1−P
(A2
))(1−P
(A3
)) =
(1− 0,3)(1− 0,2)(1− 0,4) = 0,7 ⋅0,8
⋅0,6
= 0,336.
P
(B) + P (B/) = 1
P
(B) = P (A1 + A2 + A3) = 1−P (B/) = 1−P (A1/)P (A2/)P (A3/) = 1−
0,336 = 0,664 .
Ответ.
0,664.
5.
Пловца в команду принимают следующим
образом. Сначала он должен проплыть 100
м за определенное время. Если справится,
то 400 м за определенное время. Если и с
этим справится, тогда километровую
дистанцию за определенное время. Два
спортсмена претендуют на место в команде,
причем первый вовремя преодолевает
соответствующие дистанции с вероятностями
0,7, 0,9 и 0,8, а второй – с вероятностями
0,9, 0,8 и 0,6 соответственно. Какова
вероятность того, что в команду будет
принят один из них.
Первого
примут, если он пройдет все три дистанции.
а)
P(1)=0,7*0,9*0,8=0,504.
И
не примут с вероятностью Q(1)=1-P(1)=0,496
Второго
примут с вер-тью P(2)=0,9*0,8*0,6=0,432.
И
не примут с Q(2)=1-P(2)=0,568.
Их
обоих не примут с вер-тью
Q(3)=Q(1)*Q(2)=0,496*0,568=0,282
б)
Примут хоть одного с вер-тью
P(3)=1-Q(3)=1-0,282=0,718
в)
Примут обоих с вер-тью
P(4)=P(1)*P(2)=0,504*0,432=0,218
Вер-сть,
что 1 примут, а 2 нет
p1=P(1)*Q(2)=0,504*0,568=0,286
Вер-сть,
что 2 примут, а 1 нет
p2=P(2)*Q(1)=0,432*0,496=0,214
г)
Вер-сть, что примут только одного
P(5)=p1+p2=0,286+0,214=0,5
6.
Вероятность попадания в мишень каждым
из двух стрелков равна 0,4. Стрелки
стреляют по очереди, причем каждый
должен сделать по три выстрела. Попавший
в мишень первым получает приз. Найти
вероятность того, что приз получит
первый стрелок.
Из
тетради
1.Игрок
А поочередно играет по две партии с
игроками В и С. Вероятности выигрыша
первой партии для Ви С равны 0.1 и 0.2
соответственно; вероятность выиграть
во второй партии для В равна 0.3, для С
равна 0.4. Определить вероятность того,
что
а)
первым выиграет В;
б)
первым выиграет С
Всего
играется 4 партии. Возможно несколько
взаимоисключающих исходов:
1)
В первой партии выиграет В (т. о. , В
выиграет первым) ;
2)
В первой партии выиграет А, во второй
выиграет С (т. о. , С выиграет первым) ;
3)
В первой и второй партиях выиграет А, в
третьей выиграет В (т. о. , В выиграет
первым) ;
4)
В первой, второй и третьей партиях
выиграет А, в четвертой выиграет С (т.
о. , С выиграет первым) ;
5)
Все партии выиграет А.
Других
исходов быть не может, т. е. сумма
вероятностей исходов 1-5 равна единице.
Вероятность
того, что А выиграет в 1-ой партии
Р1=1-0.1=0.9
Вероятность
того, что А выиграет в 2-ой партии
Р2=1-0.2=0.8
Вероятность
того, что А выиграет в 3-ей партии
Р3=1-0.3=0.7
Вероятность
того, что А выиграет в 4-ой партии
Р4=1-0.4=0.6
Выигрыш
в каждой партии — событие независимое.
Т. о. , по закону умножения вероятностей,
—
вероятность исхода 1: 0.1 (дано в условии)
—
вероятность исхода 2: 0.9*0.2=0.18
—
вероятность исхода 3: 0.9*0.8*0.3=0.216
—
вероятность исхода 4: 0.9*0.8*0.7*0.4=0.2016
—
вероятность исхода 5: 0.9*0.8*0.7*0.6=0.3024
В
сумме, как легко проверить, единица.
Таким
образом: вероятность того, что первым
выиграет В — это сумма вероятностей
исходов 1 и 3, а вероятность того, что
первым выиграет С — это сумма вероятностей
исходов 2 и 4. В случае исхода 5 не выиграет
первым ни В, ни С.
Находим
для В: 0.1+0.216=0.316
Для
С: 0.18+0.2016=0.3816.
2.Определить
вероятность того, что выбранное наудачу
изделие является первосортным, если
известно, что 4 % всей продукции является
браком, а 75 % небракованных изделий
удовлетворяют требованиям первого
сорта.
Решение.
Пусть
событие A={выбранное изделие небракованное},
событие B={небракованное изделие
удовлетворяет требованиям первого
сорта}, событие C={выбранное наудачу
изделие первосортное}. Событие C
предоставляет собой произведение
событий A и B: C=AB. По условию
Р(А) = 1-0,04 = 0,96,
Р(В/А) = 0,75.
Тогда по теореме умножения вероятностей
(см. 2.1) искомая вероятность
Р(АВ)
= Р(А)*Р(В/А)= 0,96*0,75=0,72.
Соседние файлы в предмете Анализ данных
- #
31.03.202020.58 Кб51КР по АД 5 вариант.xlsx
- #
- #
- #
Воспользуйтесь условной вероятностью.Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 марта 2010 23:46 | IP
Для сигнализации об аварии в двигателе установлены два независимо от работающих сигнализатора.Вероятность того что при аварии сигнализатор сработает равна0,95 для первого сигнализатора и 0,9 для второго.Найти вероятность того что при аварии а)сработает только один сигнализатор, б)сработают оба сигнализатора
2) Вероятность того что во время работы цифровой электронной машины произойдет сбой в арифметическом устройстве,в оперативной памяти,в остальных устройствах,относятся как 3:2:5.Вероятность обнаружения сбоя в арифметическом устройстве,в оперативной памяти и в остальных устройствах соответственно равны 0,8;0,9;0;9.Найти вероятность того что возникший сбой в машине будет найден.
3)Два равносильных противника играют в шахматы.Что вероятнее?
а)выиграть одну партию из двух или две партии из 4?
б)выиграть не менее 2х пртий из 4х или не менее 3х партий из 5?ничьи во внимание не принимаются
Источник
Брошены две игральные кости Найти вероятность того
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Вероятности того, что во время работы цифровой электронной машины произойдет сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах,
относятся как 3:2:5. Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.
Решение: Пусть А – событие того, что сбой будет обнаружен, тогда из формулы полной вероятности следует, что:
PA= PB1PB1A+PB2PB2A+PB3PB3A= 0,3*0,8+0,2*0,9+0,5*0,9=0,87.
Обозначим через А событие – деталь отличного качества
Можно сделать два предположения




Условная вероятность, что она будет отличного качества, если она произведена первым автоматом 
Условная вероятность, что она будет отличного качества, если она произведена первым автоматом 
Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятности равна
P(A)=Р(



Вероятность того, что взятая отличная деталь произведена первым автоматом, по формуле Бейеса равна




Ответ:
Решение: Обозначим событие А – стрелок поразил мишень и гипотезы: B1 – стрелок выбрал винтовку с оптическим прицелом, B2 – без оптического прицела. Тогда 

Теперь, воспользовавшись формулой Бейеса, получим ответ:
Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.
Решение: Обозначим через А событие—подъезд автомобиля к заправке. Можно сделать два предположения: 



Вероятность того, что проезжающий автомобиль подъедет на заправку, по формуле полной вероятности равна Р(А) = 







Искомая вероятность того, что подъехавший к заправке автомобиль будет грузовым, по формуле Бейеса равна 


Две перфораторщицы набили на разных перфораторах по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,05; для второй перфораторщицы эта вероятность равна 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица. (Предполагается, что оба перфоратора были исправны.)
Обозначим через событие А – ошибку перфораторщицы. Тогда, 



Условная вероятность того, что первая перфораторщица допустит ошибку, равна 
Условная вероятность того, что вторая перфораторщица допустит ошибку, равна 
Вероятность того, что наудачу взятая перфокарта, окажется с ошибкой равна, по формуле полной вероятности равна:
P(A)= P(




Искомая вероятность того, что взятая перфокарта произведена первой перфораторщицей, по формуле Бейеса равна:




В специализированную больницу поступают
в среднем 50% больных с заболеванием К, 30%—с за-
заболеванием L, 20%—с заболеванием М- Вероятность
полного излечения болезни К равна 0,7; для болезней L
и М эти вероятности соответственно равны 0,8 и 0,9.
Больной, поступивший в больницу, был выписан здоро-
здоровым. Найти вероятность того, что этот больной страдал
P(A)= Pk(a)*P(k) + Pl(a)*P(l) + Pm(a)*P(m) = 0.7*0.5 + 0.8*0.3 + 0.9*0.2 = 0.77
А вероятность что больной страдал именно заболеванием К равно:
Pa(K) = (Pk(a)*P(k))/P(A)= (0.5*0.7)/0.77 = 5/11
Вероятность того, что изделие будет признано стандартным по формуле полной вероятности равна
P(A)= P(



Искомая вероятность того, что изделие проверил второй товаровед, по формуле Бейеса равна




Событие А может появится при условии появления одного из несовместимых событий В1, В2,…, Вn, образующих полную группу событий. После появления события А были переоценены вероятности гипотез, то есть были найдены условные вероятности РА(Вi) (i=1,2,…,n). Доказать, что сумма РА(Вi) (i=1,2,…,n) равна 1.
Что и требовалось доказать.
Событие 





Так как события 



Имеются три партии деталей по 20 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 20, 15, 10. Из наудачу выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращают в партию
и вторично из той же партии наудачу извлекают деталь, которая также оказывается стандартной. Найти вероятность того, что детали были извлечены из третьей партии.
Обозначим через А событие – в каждом из двух испытаний была извлечена стандартная деталь. Можно предположить, что B1 – детали извлекались из первой партии; B2 – детали извлекались из второй партии; В3 – детали извлекались из третей партии.
Детали извлекались на удачу, поэтому вероятности предположений одинаковы:
P(B1) = P(B2) = P(B3) =
Вероятность того, что из первой партии будут последовательно извлечены две стандартные детали; поэтому
Условная вероятность 
Найдем условную вероятность 
Искомая вероятность того, что обе извлеченные детали стандартные взяты из третей партии, по формуле Бейеса равна
Ответ:
Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания в цель первым, вторым и третьим орудиями соответственно равны 


Обозначим через A событие- два орудия попали в цель. Сделаем два предположения: 
По условию 

Найдем условную вероятность 
Искомая вероятность того, что первое орудие дало попадание, по формуле Бейеса равна:

Ответ:
Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,6, 0,5 и 0,4.
Решение. Обозначим через А событие – две пули поразили мишень. Сделаем два предположения (гипотезы): В1 – третий стрелок поразил мишень; В2 – третий стрелок не попал в мишень.
По условию, Р(В1) = 0,4; следовательно (событие В2 противоположно событию В1),
Найдем условную вероятность РВ1(А), т.е. вероятность того, что мишень поразили две пули, причем одна из них принадлежит третьему стрелку и, следовательно, вторая – либо первому стрелку (при этом второй не попал), либо второму стрелку (при этом первый не попал). Эти два события несовместны, поэтому применима теорема сложения:
РВ1(А) = p1∙q2 + p2∙q1 = 0,6∙0,5 + 0,5∙0,4 = 0,5.
Найдем условную вероятность РВ2(А), т.е. вероятность того, что мишень поразили две пули, причем третий стрелок промахнулся. Другими словами, найдем вероятность того, что первый и второй стрелки поразили мишень. Эти два события независимы, поэтому применима теорема умножения:
РВ2(А) = p1∙p2 = 0,6∙0,5 = 0,3.
Искомая вероятность того, что третий стрелок поразил мишень, по формуле Бейеса равна
РА(В1) = Р(В1)∙РВ1(А)/[ Р(В1)∙РВ1(А) + Р(В2)∙РВ2(А)] = 0,4∙0,5/( 0,4∙0,5 + 0,6∙0,3 ) = 10/19.
Два из трех независимо работающих элементов вычислительного устройства отказали. Найти вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, второго и третьего элементов соответственно равны 0,2; 0,4 и 0,3.
Решение. Обозначим через А событие – отказали два элемента. Можно сделать следующие предположения (гипотезы):
Р(В1) = p1∙p2∙q3 = 0,2∙0,4∙0,7 = 0,056;
Р(В2) = p1∙p3∙q2 = 0,2∙0,3∙0,6 = 0,036;
Р(В3) = p2∙p3∙q1 = 0,4∙0,3∙0,8 = 0,096;
Вероятности последних трех гипотез не вычислены, так как при этих гипотезах событие А (отказали два элемента) невозможно и значит условные вероятности РВ4(А), РВ5(А) и РВ6(А) равны нулю, следовательно, равны нулю и произведения Р(В4)∙РВ4(А), Р(В5)∙РВ5(А) и Р(В6)∙РВ6(А) при любых значениях вероятностей гипотез В4, В5 и В6.
Поскольку при гипотезах В1, В2 и В3 событие А достоверно, то соответствующие условные вероятности равны единице:
РВ1(А) = РВ2(А) = РВ3(А) = 1.
По формуле полной вероятности, вероятность того, что отказали два элемента, равна
Р(А) = Р(В1)∙РВ1(А) + Р(В2)∙РВ2(А) + Р(В3)∙РВ3(А) + Р(В4)∙РВ4(А) + Р(В5)∙РВ5(А) + Р(В6)∙РВ6(А) = 0,056 + 0,036 + 0,096 = 0,188.
По формуле Бейеса, искомая вероятность того, что отказали первый и второй элементы,
РА(В1) = Р(В1)∙РВ1(А)/ Р(А) = 0,056/0,188 = 0,3.
Две из четырех независимо работающих ламп прибора отказали. Найти вероятность того, что отказали первая и вторая лампы, если вероятности отказа первой, второй, третьей и четвертой ламп соответственно равны 0,1, 0,2, 0,3 и 0,4.
Решение. Обозначим через А событие – отказали две лампы. Можно сделать следующие предположения (гипотезы):
Р(В1) = p1∙p2∙q3∙q4 = 0,1∙0,2∙0,7∙0,6 = 0,0084;
Р(В2) = p1∙q2∙p3 ∙q4 = 0,1∙0,8∙0,3∙0,6 = 0,0144;
Р(В3) = p1∙q2∙q3∙p4 = 0,1∙0,8∙0,7∙0,4 = 0,0224;
Р(В4) = q1∙p2∙p3∙q4 = 0,9∙0,2∙0,3∙0,6 = 0,0324;
Р(В5) = q1∙p2∙q3∙p4 = 0,9∙0,2∙0,7∙0,4 = 0,0504;
Р(В6) = q1∙q2∙p3∙p4 = 0,9∙0,8∙0,3∙0,4 = 0,0864;
Вероятности последних четырех гипотез не вычислены, так как при этих гипотезах событие А (отказали две лампы) невозможно и значит условные вероятности РВ7(А), РВ8(А), РВ9(А) и РВ10(А) равны нулю, следовательно, равны нулю и произведения Р(В7)∙РВ7(А), Р(В8)∙РВ8(А), Р(В9)∙РВ9(А) и Р(В10)∙РВ10(А) при любых значениях вероятностей гипотез В7, В8, В9 и В10.
Поскольку при гипотезах В1 – В6 событие А достоверно, то соответствующие условные вероятности равны единице:
РВ1(А) = РВ2(А) = РВ3(А) = РВ4(А) = РВ5(А) = РВ6(А) = 1.
По формуле полной вероятности, вероятность того, что отказали две лампы, равна
Р(А) = Р(В1)∙РВ1(А) + Р(В2)∙РВ2(А) + Р(В3)∙РВ3(А) + Р(В4)∙РВ4(А) + Р(В5)∙РВ5(А) + Р(В6)∙РВ6(А) + Р(В7)∙РВ7(А) + Р(В8)∙РВ8(А) + Р(В9)∙РВ9(А) + Р(В10)∙РВ10(А) = 0,0084 + 0,0144 + 0,0224 + 0,0324 + 0,0504 + 0,0864 = 0,2144.
По формуле Бейеса, искомая вероятность того, что отказали первая и вторая лампы, равна
РА(В1) = Р(В1)∙РВ1(А)/ Р(А) = 0,0084/0,2144
Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три из шести (ничьи во внимание не принимаются)?
Играют равносильные шахматисты, поэтому вероятность выигрыша p=1/2; следовательно, вероятность проигрыша q также равна 1/2. Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли.
Найдем вероятность того, что две партии из четырех будут выиграны:
Найдем вероятность того, что выиграны три партии из шести:
Так как P4(2)>P6(3), то вероятнее выиграть две партии из четырех, чем три из шести.
Два равносильных противника играют в шахматы. Что вероятнее: а) Выиграть одну партию из двух или две партии из четырех? б)выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаються.
Играют равносильные шахматисты, поэтому вероятность выигрыша 

А) Найдем вероятность того, что две партии из четырех будут выиграны:
Найдем вероятность того, что одна партия из двух будет выиграна:
Б) Найдем вероятность выиграть не менее двух партий из четырех:
Найдем вероятность выиграть не менее трех партий из пяти:
Монету бросают пять раз. Найти вероятность того, что “герб” выпадет: а)мене двух раз; б)не менее двух раз.
При бросании монеты вероятность выпадения герба и решки, равновероятны, поэтому вероятность выпадения герба равна 

А) Найдем вероятность того, что герб выпадет менее двух раз:



Б) Найдем вероятность того, что герб выпадет не менее двух раз:

Ответ: a) 
Источник
Вам также понравится
Определение вероятности того, что две наиболее сильные команды окажутся в одной подгруппе. Расчет вероятности выбора детали первого сорта. Расчет вероятности допущенной ошибки
Страницы работы
Фрагмент текста работы
наудачу выбранная из
изготовленных в цехе деталь окажется изделием первого сорта.
Решение
Обозначим события: .
А = {производство стандартной детали}
B={производство детали первого сорта}
По условию:
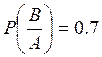
,
Отсюда
В данном случае B может осущетвиться только
одновременно с осуществлением события А, то есть По
теореме умножения вероятностей:
Таким образом, вероятность
производство первого сорта раина 0,868.
Ответ: 0,868
Задача№4
Электрическая цепь на
участке MN собрана по схеме, изображенной на рисунке. Каждый из
элементов e1 – e7 выходит из строя независимо от других. Надежность
(вероятность безотказной работы в течение заданного промежутка времени) каждого
из элементов равна 0,9. Предполагая, что сбой в цепи может произойти только
вследствие нарушения функционирования элементов e1 – e7, найти надёжность участка цепи MN.
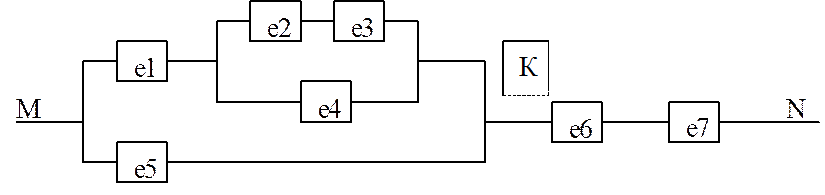
Решение
Обозначим события
безотказная
работа i-го элемента в течении времени T}
i=1,2…7;
{безотказная работа в течении времени
T участка цепи NK}
C- {безотказная работа всего участка
цепи MK в течении времени T}
D- {одновременно безотказная работа ,
и
функционирование }
Событие С представим в виде , то есть для функционирования участка
цепи MK необходимо безотказное
функционирование участков MKи KN.
Для обеспечения функционирования
участка MN необходимо хотя бы одно условие:
1.
Безотказная
работа элемента
2.
Безотказная
работа элемента и одновременно безотказная
работа ,
и
функционирование .
Для определения вероятности применяем
теорему сложения вероятностей совместных событий и теорему умножения
вероятностей независимых событий.
Для функционирования участка KN необходима безотказная работа элементов и
.
Для вычисления вероятности перейдем
к рассмотрению события , состоящего в отказе цепи KN. Для осуществления события
необходим одновременный выход из строя
хотя бы одного из элементов или
.
Учитывая, что события и
— совместны получим:
,
где .
Отсюда
Окончательно вероятность события С:
Ответ: 0,7276
Задача№5
Вероятность
того, что при одном измерении некоторой физической величины будет допущена
ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых
испытания. Найти вероятность того, что только в одном из них допущенная ошибка
превысит заданную точность. Р=0,432
Решение
Е: производят
измерения некоторой физической величины.
А={ошибка
превысит заданную точность в первом эксперименте}
В={ошибка
превысит заданную точность во втором эксперименте}
С={ошибка превысит заданную
точность в третьем эксперименте}
D={ошибка превысит заданную точность в}
P(D)-?
P(A)=0.4
P(B)=0.4
P(C)=0.4
Т.к. события ,
и
не совместны, а события А, В и С не зависимы,
то вероятность наступления события D по
теореме сложения вероятностей:
Ответ: Р(D)=0.432
Задача№6
Вероятности
того, что во время работы ЭВМ возникает сбой в арифметическом устройстве, в
оперативной памяти, в остальных устройствах, соотносятся так: 3:2:5.
Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти
и в остальных устройствах соответственно равны 0,8;0,9;0,9. Найти вероятность
того, что возникший в машине сбой будет обнаружен. Р=0,87
Решение
Е: испытание
ЭВМ
А={сбой будет
обнаружен в ЭВМ }
В={сбой произойдет
и будет обнаружен в арифметическом устройстве }
С={сбой произойдет
и будет обнаружен в оперативной памяти}
Похожие материалы
- Парадокс из теории игр. Парадокс гладиатора
- Работа с пакетом STATGRAPHICS Plus 5.0: Учебно-методическое пособие
- Расчет вероятности выхода пассажиров из лифта на одном этаже. Определение вероятности того, что участок АС поезд пройдет без остановки
Информация о работе
Тип:
Расчетно-графические работы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.