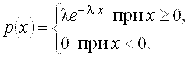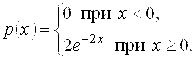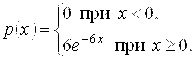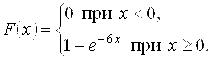Время безотказной работы элемента распределено по показательному закону - Контакты компаний и предприятий на Atlaso.ru

Задача 29119 4. Время безотказной работы элемента…

Условие

4. Время безотказной работы элемента распределено по показательному закону f(t) = 0,01e^(-0,01t) (t > 0), где t — время, ч. Найти
вероятность того, что элемент проработает безотказно 100 ч.
Отв. R (100) = 0,37.

математика ВУЗ
4544

Решение

★

Функция надежности в случае распределения случайной величины по показательному закону имеет вид:
R(t)=1- F(t)=1-(1-e^(-лямбдаt)= e^(-лямбда t)

По условию,
лямбда =0,01
t=100

R (100) = е^(-0,01*100)=е^(-1) = 1/e ≈ 0,37.

О т в е т.
Вероятность того, что элемент проработает безотказно 100 ч, приближенно равна 0,37.

Написать комментарий

Источник

Информация о материале: Категория: Глава 13. Показательное распределение; Опубликовано: 14 сентября 2018; Просмотров: 9377

Глава 13. Задача 4. Время безотказной работы элемента распределено по показательному закону (f(x) = 0,01e^{-0,01t}) ((t > 0)), где (t) — время, ч. Найти вероятность того, что элемент проработает безотказно 100 ч.

Решение.

Показательным законом надежности называют функцию надежности, определяемую равенством

[R(t) = e^{-lambda t}, qquad (*)]

где (lambda) — интенсивность отказов.

Эта формула позволяет найти вероятность безотказной работы элемента на интервале времени длительностью (t), если время безотказной работы имеет, показательное распределение.

По условию задачи, постоянная интенсивность отказов (lambda = 0,01).

Воспользуемся формулой (*):

[R(100) = e^{-0,01cdot 100} = e^{-1} approx 0,37.]

Ответ. (R(100) = 0,37).

Источник

В настоящем пункте условимся
называть элементом
некоторое устройство независимо оттого,
что оно «простое»
или «сложное».
Пусть элемент начинает работать в
момент времени,
а по истечении времени длительностьюпроисходит отказ. Обозначим через— непрерывную случайную величину
«длительность времени безотказной
работы элемента за время».
Если элемент проработал безотказно
некоторое время (скажем),
меньшее чем,
а затем перестал работать, тогда
обязательно за время длительностьюнаступит отказ работы элемента.

Таким образом, функция
распределения
определяет вероятность отказа за время
длительностьюСледовательно, вероятность безотказной
работы за это же время длительностью,
(т.е. вероятностью противоположного
событияравна

(25)

Функцию, определяющую вероятность безотказной
работы элемента за время длительностью
,
называют функцией надёжности:

Далее, определим так
называемый показательный
закон надёжности.
Часто длительность времени безотказной
работы элемента имеет показательное
распределение, функция распределения
которого (см. равенство 1.
п. 6., теорема 6) равна

(26)

где
интенсивность отказов, т.е. среднее
число отказов за единицу времени.

Следовательно, в силу формул
(25) и (26) для функции надёжности в случае
показательного распределения вероятность
безотказной работы элемента за время
длительностью
получим равенство

Показательным законом надёжности
называют функцию надёжности, определённую
равенством

(27)

Как следует из формулы
(27), если время безотказной работы
элемента имеет показательное
распределение, то эта формула позволяет
найти вероятность безотказной работы
элемента на интервале времени
длительностью
.

Пример
10. Время безотказной
работы элемента распределено по
показательному закону

Найти вероятность того, что элемент
проработает безотказно 100 часов.

Решение. По
условию постоянная интенсивность
отказов
Воспользуемся равенством (27), тогда

Искомая вероятность того,
что элемент проработает безотказно
100 ч., приближённо равна
Далее, также следует отметить о том,
что функция надёжности связана с
простейшим потоком события (см. Т.
6., п.3.), где в распределении
Пуассона, при

Полученное равенство ещё раз подтверждает
следующего факта: если отказы элементов
в случайные моменты времени образуют«простейший поток», то вероятность
того, что за время длительностьюне наступит ни одного отказа.

Наконец, отметим, что имеет
место и другое важное равенство
плотность
показательного распределения.

8. Характеристическое свойство показательного

закона
надёжности

Показательный закон
надёжности весьма прост и удобен для
решения практических задач. Как правило.
многие формулы теории надежности
значительно упрощаются. Это объясняется
тем, что данный закон является
единственный из законов распределения,
который обладает свойством «отсутствия
последействия». А
именно имеет место утверждение.

Теорема 9.7.
Вероятность безотказной
работы элемента на интервале времени
длительностью
не зависит от времени предшествующей
работы элемента до начала рассматриваемого
интервала, а зависит только от
длительности времени(при заданной интенсивности отказов).

Доказательство. Введём
обозначения событий:
—
безотказная работа элемента на интерваледлительностью;—
безотказная работа элемента на интерваледлительностью.
Тогдабезотказная работа элемента на интерваледлительностьюНайдём вероятности этих событий по
формуле (25):

(28)
.

Далее, вычислим условную
вероятность того, что элемент будет
работать безотказно на интервале
при условии, что он уже проработал
безотказно на предществующем интервале.
Применяя, теорему умножения вероятностей
получим

Как видим, полученная
формула не содержит
,
а содержит только.
Это и означает, что время работы элемента
на предшествующем интервале не повлияет
на величине вероятности безотказной
работы элемента на последующем интервале,
а зависит только от длины этого интервала,
что и требовалась доказать.

Сравнив вероятности,
полученные в формуле (28)
заключаем: условная вероятность
безотказной работы элемента на интервале
длительностью
вычисленная в предположении, что элемент
проработал безотказно на предшествующем
интервале, равна безусловной вероятности.

Замечание. Можно
доказать, что рассматриваемым свойством
обладает только показательное
распределение. Таким образом, если на
практике исследуемая с.в.
этим свойством обладает, то она
распределена по показательному закону.

Например,
при допущении факта, что метеориты
распределены равномерно в пространстве
и во времени, то вероятность столкновения
их с космическим кораблём не зависит
от того, попадали или не попадали они
в корабль до начала рассматриваемого
интервала времени. Следовательно,
случайные моменты времени попадания
метеоритов в космический корабль
распределены по показательному закону.

Упражнение. Определить
множество точек, для которых функция

является
функцией плотности показательного
закона, если
ицелые
числа. Найти это множество точек на
плоскости.

Соседние файлы в папке Теория вероятностей от исмоилова

#
#
#
#
#
#
#
06.02.20162.36 Mб66~WRL0002.tmp
#
06.02.20161.87 Mб62~WRL0005.tmp
#
06.02.20161.01 Mб61~WRL0205.tmp
#
06.02.20162.41 Mб60~WRL0264.tmp
#
06.02.20162.17 Mб60~WRL0310.tmp

Источник

Показательное распределение

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины

, которое описывается плотностью:

где

–
постоянная положительная величина.

Показательное
распределение определяется одним параметром

. Эта особенность распределения указывает на
его преимущество по сравнению с распределениями, зависящими от большего числа
параметров. Обычно параметры неизвестны и приходится находить их оценки
(приближенные значения); разумеется, проще оценить один параметр, чем два или три.
Примером непрерывной случайной величины, распределенной по показательному
закону, может служить время между появлениями двух последовательных событий
простейшего потока.

Функция распределения
показательного закона:

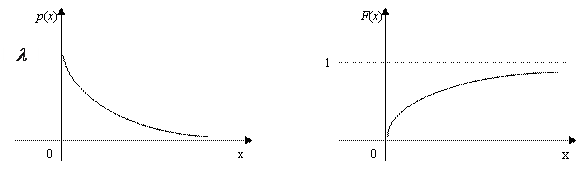
Графики плотности и
функции распределения показательного закона изображены на рисунке.

Вероятность попадания в
интервал

непрерывной
случайной величины

, распределенной по показательному закону:

Числовые характеристики показательного (экспоненциального) распределения

Математическое ожидание случайной величины, распределенной по показательному закону:

Дисперсия случайной величины, распределенной по показательному закону:

Среднее квадратическое отклонение случайной величины,
распределенной по показательному закону:

Коэффициенты асимметрии и эксцесса
для показательного распределения:

Таким
образом, математическое ожидание и среднее квадратическое
отклонение экспоненциального распределения равны между собой.

Показательный закон
распределения играет большую роль в теории массового обслуживания и теории
надежности. Так, например, интервал времени

между
двумя соседними событиями в простейшем потоке имеет показательное распределение
с параметром

–
интенсивностью потока.

При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.

Смежные темы решебника:

Непрерывная случайная величина
Нормальный закон распределения случайной величины
Равномерный закон распределения случайной величины

Примеры решения задач

Пример 1

Случайная величина

задана функцией распределения

Найдите математическое
ожидание и среднее квадратическое отклонение этого
распределения.

Найдите вероятность того,
что случайная величина примет значение от 0,2 до 1.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Математическое
ожидание случайной величины, распределенной по показательному закону:

Среднее
квадратическое отлонение:

Вероятность того, что
случайная величина примет значение от 0,2 до 1

Ответ

Пример 2

На шоссе установлен контрольный пункт для
проверки технического состояния автомобилей. Найти математическое ожидание и
среднее квадратическое отклонение случайной величины T – время ожидания
очередной машины контролером, если поток машин простейший и время (в часах)
между прохождениями машин через контрольный пункт распределено по
показательному закону f(t)=5e^-5^t.

Указание: Время ожидания машины
контролером и время прохождения машин через контрольный пункт распределены
одинаково.

Решение

В нашем случае
параметр показательного распределения

Математическое
ожидание:

Дисперсия:

Среднее
квадратическое отклонение:

Ответ:

Пример 3

Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите математическое ожидание M(X), дисперсию D(X),
среднее квадратическое отклонение σ(X), моду x_mod, медиану x_med, если известно, что
случайная величина X имеет показательное распределение с параметром λ=1.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Плотность
распределения случайной величины

, распределенной по
показательному закону:

Функция
распределения:

Построим
графики дифференциальной и интегральной функций распределения:

График дифференциальной функции распределения

График интегральной функции распределения

Математическое
ожидание показательно распределенной случайной величины

Дисперсия:

Среднее
квадратическое отклонение:

найдем, исходя из условия:

Пример 4

Случайная
величина

распределена показательно с дисперсией 0,25.
Найти математическое ожидание и вероятность попадания

в интервал (0,5;1).

Решение

Дисперсия
случайной величины, распределенной по показательному закону:

Математическое
ожидание случайной величины, распределенной по показательному закону:

Вероятность
попадания в интервал

непрерывной случайной величины

, распределенной по
показательному закону:

В нашем
случае:

Ответ:

Задачи контрольных и самостоятельных работ

Задача 1

Время
безотказной работы двигателя автомобиля распределено по показательному закону.
Известно, что среднее время наработки двигателя на отказ между техническим
обслуживанием 100 ч. Определить вероятность безотказной работы двигателя за 80
ч.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 2

Среднее
время работы элемента, входящего в пожарно-техническое устройство, равно 1000
часов. Определить вероятность того, что элемент будет работать от 950 до 1150
часов, если время работы элемента распределено по показательному закону.

Задача 3

Вероятность
безотказной работы элемента распределена по экспоненциальному закону

f(t)=e^-0.05t

Найти
вероятность того, что в результате испытания случайная величина попадет в
интервал (11;35). Найти характеристики данного распределения случайной
величины.

Задача 4

Непрерывная
случайная величина X задана интегральной функцией распределения

Найти
постоянную C, математическое ожидание случайной величины X,
вероятность попадания случайной величины в интервал [2;4].

Задача 5

Время
между отказами прибора распределено по показательному закону со средним
значением 25 часов. Определить математическое ожидание и дисперсию времени
безотказной работы автомобиля. Найти вероятность того, что очередной отказ
произойдет не позднее 15 часов.

Задача 6

Время
безотказной работы телевизора определенной модели описывается показательным (экспоненциальным)
законом распределения с постоянной λ. Что вероятнее, его безотказная работа в
промежутке времени [x₁,x₂]

или [x₃,x₄]? Записать
функции f(x),F(x) и построить их графики.

λ=1/10, x₁=3, x₂=5, x₃=4, x₄=8

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 7

Испытывают
два независимо работающих элемента. Длительность времени t безотказной
работы первого элемента имеет показательное распределение с параметром 0,02,
второго -показательное распределение с параметром 0,06. Найдите вероятность
того, что за время длительностью t=6 ч откажет только один
элемент.

Задача 8

Среднее
время работы каждого из трех элементов, входящих в техническое устройство,
равно T=850 часов. Для безотказной работы устройства необходима безотказная
работа хотя бы одного из трех этих элементов. Определить вероятность, что
устройство будет работать от t₁=750 до t₂=820 часов, если время
работы каждого из трех элементов независимо и распределено по показательному
закону.

Задача 9

Время
устранения повреждения на канале связи T -случайная величина,
распределенная по закону f(t)=λe^-λt (t≥0). Среднее время
восстановления канала — 10 минут. Определить вероятность того, что на
восстановление канала потребуется от 5 до 10 минут.

Задача 10

Дана плотность
распределения случайной величины X.

По какому
закону распределения случайная величина? Найти математическое ожидание,
дисперсию, функцию распределения?

Задача 11

Время
безотказной работы механизма подчинено показательному закону с плотностью
распределения вероятностей f(t)=0.04e^-0.04t при t > 0 (t –
время в часах). Найти вероятность того, что механизм проработает безотказно не
менее 100 часов.

Задача 12

Длительность телефонного разговора
является случайной величиной, распределенной по показательному закону.
Известно, что средняя длительность телефонного разговора равна 9 минутам. Найти
вероятность того, что разговор будет длиться:

а) не более 5 минут.

б) более 5 минут.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 13

Случайная величина ξ подчинена
показательному закону с параметром λ=5:

Найдите вероятность того, что
случайная величина ξ примет значение меньшее, чем ее математическое ожидание.

Задача 14

Случайная
величина ξ имеет плотность вероятностей (показательное распределение)

Найдите
вероятность P{ξ>M_ξ}

Задача 15

Время T
(минут), затрачиваемое клиентами парикмахерской в ожидании своей очереди,
удовлетворяет показательному распределению с параметром λ=0,05. Какова
вероятность того, что время ожидания превысит 25 минут и каково среднее время
ожидания.

Задача 16

Время T (час),
необходимое на ремонт легкового автомобиля удовлетворяет показательному
распределению с параметром λ=0,2. Какова вероятность того, что время ремонта
одного автомобиля не превысит 6 часов, и сколько часов в среднем затрачивается
на ремонт одного автомобиля.

Задача 17

Время
ожидания у бензоколонки автозаправочной станции является случайной величиной X,
распределенной по показательному закону, со средним временем ожидания, равным t₀. Найти вероятности
следующих событий:

Задача 18

Случайная
величина X задана показательным законом распределения и
числовыми значениями параметров M(X)=3 и σ_x=3.

Требуется:

1) найти
функцию плотности f(x).

2) найти
вероятность попадания СВ X в указанный интервал [a,b]=[2,4].

Задача 19

Случайная
величина ξ задана функцией распределения

Найдите
математическое ожидание и среднее квадратическое отклонение этого
распределения.

Задача 20

Случайная величина ξ распределена по
показательному закону с параметром λ=0,3. Найдите математическое ожидание и
среднее квадратическое отклонение этой случайной величины.

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник

Непрерывная случайная величина Х имеет Показательный (экспоненциальный) закон распределения с параметром λ, если ее плотность вероятности имеет вид

Функция распределения случайной величины, распределенной по показательному закону, равна

Кривая распределения Р(Х) и график функции распределения приведены на рис. 8.13.

Рис. 8.13

Для случайной величины, распределенной по показательному закону

; .

Вероятность попадания в интервал непрерывной случайной величины Х, распределенной по показательному закону

Замечание. Показательный закон распределения вероятностей встречается во многих задачах, связанных с простейшим потоком событий. Под Потоком событий понимают последовательность событий, наступающих одно за другим в случайные моменты. Например, поток вызовов на телефонной станции, поток заявок в системе массового обслуживания и др.

Пример 8.18. Непрерывная величина Х распределена по показательному закону

Найти вероятность попадания значений величины Х в интервал .

Решение. Поскольку , то

Пример 8.19. Записать плотность распределения и функцию распределения показательного закона, если параметр . Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, распределенной по этому закону.

Решение. Так как , то плотность распределения

Функция распределения имеет вид

Поскольку для показательного закона

; ,

А по условию , то

Пример 8.20. Установлено, что время ремонта магнитофонов есть случайная величина Х, распределенная по показательному закону. Определить вероятность того, что на ремонт магнитофона потребуется не менее 15 дней, если среднее время ремонта магнитофонов составляет 12 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины Х.

Решение. По условию математическое ожидание , откуда параметр . Тогда плотность вероятности и функция распределения имеют вид: ; . Искомую вероятность можно найти, интегрируя плотность вероятности, т. е.

Но проще использовать функцию распределения

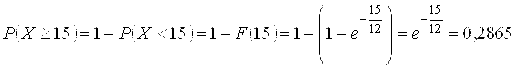
Среднее квадратическое отклонение Дней.

Пример 8.21. Найти асимметрию показательного распределения.

Решение. Так как асимметрия , а , то найдем вначале центральный момент третьего порядка

Найдем

Интегрируя дважды по частям, получим

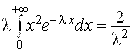
Аналогично рассчитаем

Следовательно,

Значит,

Часто длительность времени безотказной работы элемента имеет показательное распределение, функция распределения которого определяет Вероятность отказа элемента за время длительностью T. Здесь Т — длительность времени безотказной работы элемента, — интенсивность отказов (среднее число отказов в единицу времени).

Функция надежности определяет вероятность безотказной работы элемента за время длительностью T.

Пример 8.22. Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента ; для второго ; для третьего элемента Найти вероятности того, что в интервале времени часов откажут: а) только один элемент; б) только два элемента; в) все три элемента.

Решение. А) Вероятность отказа первого элемента

;

Второго элемента

;

Третьего элемента

Следовательно, искомая вероятность

Б) .

В) .

< Предыдущая		Следующая >

Источник

Начинающий

Зарегистрирован:
09 мар 2022, 00:49
Сообщений: 14
Cпасибо сказано: 1
Спасибо получено:
0 раз в 0 сообщении
Очков репутации: 1

1. Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента F1(t)=1-е^(-0,1t), для второго F2(t)=1-е^(-0,2t), для третьего F3(t)=1-е^(-0,3t). Найти вероятности того, что в интервале времени (0,5) ч откажут:
а) только один элемент;
б) только два элемента;
в) все три.

Источник